考虑天线罩误差的雷达导引头隔离度影响与UKF在线补偿

宗睿， 林德福， 兰玲， 王辉

(1.北京理工大学 宇航学院，北京 100081；2.北京航天新风机械设备有限责任公司，北京 100854)

考虑天线罩误差的雷达导引头隔离度影响与UKF在线补偿

宗睿1， 林德福1， 兰玲2， 王辉1

(1.北京理工大学 宇航学院，北京 100081；2.北京航天新风机械设备有限责任公司，北京 100854)

针对雷达导引头隔离度对导弹制导控制系统带来的严重影响，建立了包含天线罩误差在内的雷达导引头隔离度模型，对比分析了弹簧力矩、阻尼力矩及天线罩误差引起的隔离度寄生回路稳定性和时域频域性能，并研究了不同干扰输入条件下导弹脱靶量与隔离度幅值的对应关系，重点提出了一种基于无迹卡尔曼滤波(UKF)的隔离度在线补偿方法，并进行了仿真验证. 研究结果表明，导引头隔离度的存在会削弱制导控制系统稳定性、降低制导精度，其中负的天线罩误差斜率影响最为严重；闪烁噪声输入下，负的天线罩误差斜率和弹簧力矩隔离度引起的脱靶量较大，而在目标随机机动输入下，正、负天线罩误差斜率隔离度引起脱靶量较大；所提出的UKF隔离度在线补偿方法分别在速度指向误差和目标常值机动输入下均能够同时估计出弹簧力矩系数、阻尼力矩系数和天线罩误差斜率，并实现了对隔离度的有效抑制，达到了改善制导性能，提高制导精度的目的.

雷达导引头；天线罩误差；隔离度寄生回路；无迹卡尔曼滤波；在线补偿

平台导引头的稳定平台可使导引头很好地隔离弹体扰动，但是导引头内部导线拉扯及各部件摩擦等因素会使这种隔离并不完全，从而导致弹体扰动耦合进入导引头，影响导引头的输出精度，引起隔离度问题.

隔离度表征了导引头对弹体扰动的去耦能力，它的存在不仅对导引头的输出产生不利影响，更严重的是将会恶化制导控制系统稳定性，降低导弹的制导精度[1-3]. 目前，学者对导引头隔离度的建模一般只停留在以干扰力矩为主的导引头内部因素上，李富贵等[4]结合红外图像导引头对干扰力矩引起的隔离度传递函数及其寄生回路稳定性进行了分析，指出影响寄生回路稳定性最严重的区域位于中频段. 徐平等[5]研究了激光半主动导引头隔离度对末制导炮弹制导精度的影响，指出隔离度的存在会导致制导精度下降. 宋韬等[6]研究了雷达噪声输入下平台导引头干扰力矩隔离度与脱靶量的关系，指出隔离度会放大噪声对导弹脱靶量的影响. 然而，对于雷达导引头来说，除了干扰力矩的影响之外，导引头天线罩带来的天线罩误差同样会引起隔离度问题，因此在分析雷达导引头隔离度影响时，必须将天线罩误差也考虑在内.

针对导引头隔离度带来的一系列不利影响，在工程上，技术人员一般采用柔化导线、润滑机械部件等工艺方法来降低隔离度. Masten[7]提出可以在导引头稳定回路增加一个滞后校正环节，通过提高稳定回路开环增益达到降低隔离度影响的目的. 这些方法在工程上虽然易于实现，但是对隔离度的补偿和抑制效果仍然有限，因此对导引头隔离度进行实时估计与在线补偿已经成为隔离度抑制技术的最新发展方向. 目前，国内外已经有学者单独就天线罩误差斜率的在线补偿方法进行了探讨[8-9]，但在导引头隔离度领域还很少有研究人员涉及，仅Lin[10]和徐娇[11]分别用神经网络算法和扰动观测器对隔离度进行在线抑制，但前者算法复杂、收敛时间较慢，后者受建模误差和量测噪声的影响较大.

本文建立了包含干扰力矩和天线罩误差在内的雷达导引头隔离度模型，对比分析了弹簧力矩、阻尼力矩及天线罩误差引起的隔离度寄生回路稳定性及其时域频域性能，研究了不同干扰输入条件下隔离度对制导精度的影响，同时提出了一种基于UKF的隔离度在线补偿方法，并进行了仿真验证.

1 雷达导引头隔离度模型的建立

对于平台导引头来说，引起导引头隔离度的因素为反电动势和干扰力矩. 通常反电动势系数很小，单纯由此引起的隔离度幅值一般在1%以内，在分析时常常忽略其影响，而引起平台导引头隔离度问题的主要因素为干扰力矩. 干扰力矩主要由弹簧力矩和阻尼力矩组成. 弹簧力矩是由导引头平台与基座之间的导线拉扯引起的，与导引头框架角相关；阻尼力矩是由导引头框架转动连接处的动、静摩擦引起的，与导引头框架角速度相关. 这两种力矩的产生会形成干扰力矩回路，从而改变电机负载力矩，影响导引头输出角速度，进而造成隔离度问题.

针对雷达寻的体制的平台导引头来说，天线罩误差也是引起导引头隔离度的主要因素. 天线罩的外形和材质会导致雷达波穿过天线罩时发生折射效应，造成天线罩瞄准误差角，进而对导引头输出角速度产生影响，引起隔离度问题. 天线罩误差角是导引头框架角的函数，其斜率称为天线罩误差斜率.

因此，在进行雷达平台导引头隔离度分析时，必须将天线罩误差的影响也考虑在内. 由此可建立包含弹簧力矩、阻尼力矩和天线罩误差在内的平台导引头隔离度完整模型如图1所示.

图1中：Kn为弹簧力矩系数；Kω为阻尼力矩系数，由于干扰力矩始终与导引头电机负载力矩相反，因此系数Kn与Kω均大于0.Rφ为天线罩误差斜率，其符号具有不确定性，在导弹飞行过程中Rφ>0和Rφ<0的情况均有可能存在. 典型平台导引头参数如表1所示.

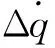
(1)

由图1可以推导出分别由弹簧力矩、阻尼力矩和天线罩误差引起的隔离度传递函数为

表1 典型平台导引头参数

Kn)(Ls+R)+sKEKT+sK2KTGgG2+

(2)

sKω)(Ls+R)+sKEKT+sK2KTGgG2+

(3)

[Js2(Ls+R)+sKEKT+sK2KTGgG2+

(4)

由式(2)～(4)可以看出，导引头隔离度不仅仅是幅值特性，还与导引头各环节的参数与动力学密切相关. 在工程中，一般以弹体频率处的隔离度幅值表征隔离度的影响. 不同弹体频率处隔离度幅值与弹簧力矩系数、阻尼力矩系数和天线罩误差斜率的关系如图2所示.

由图2所示可知，随着Kn，Kω和Rφ的增大，隔离度幅值均不断增大，且基本呈线性增长关系. 对于Kn和Kω而言，弹体频率越高，隔离度幅值越大；而对于Rφ，弹体频率越高，隔离度幅值反而越小.

以下分析中选取弹体频率2 Hz处的隔离度幅值表征不同Kn，Kω和Rφ的取值.

2 隔离度寄生回路

在导弹制导过程中，导引头隔离度的存在致使导引头输出错误的视线角速度，经制导滤波器后的视线角速度信号根据相应的制导律生成过载指令传递给驾驶仪，弹体响应该指令后改变弹体姿态，而弹体姿态的改变经过隔离度模型又会使得导引头产生新的错误输出，由此形成了一个附加的闭环回路，称为隔离度寄生回路.

2.1 寄生回路稳定性对比分析

导引头隔离度引起的寄生回路等效模型如图3所示.

由图3可得隔离度寄生回路闭环传函为

(5)

式(5)的特征方程决定了寄生回路的稳定性，取典型空空导弹参数N=4，vc/vm=2，利用劳斯判据可得到弹簧力矩、阻尼力矩及天线罩误差引起的隔离度寄生回路稳定边界曲线，如图4所示.

由图4可知，隔离度幅值越大，寄生回路越容易失稳. 当隔离度幅值相同时，不同因素引起的隔离度寄生回路稳定区域存在区别. 其中正的天线罩误差斜率引起的隔离度寄生回路稳定区域最大；相比之下，导引头干扰力矩引起的隔离度寄生回路稳定域明显缩小，其中阻尼力矩的稳定域要稍大于弹簧力矩；而负的天线罩误差斜率引起的隔离度寄生回路稳定域最小. 以上结论表明，导引头隔离度寄生回路对于正的天线罩误差斜率的要求较为宽松，导引头干扰力矩次之，而对负的天线罩误差斜率最为敏感，此时寄生回路更容易失稳，对制导控制系统参数的选取也更为严格.

2.2 寄生回路频域与时域性能

由图5所示可知，当N=4，vc/vm=2时，正的天线罩误差斜率引起的隔离度寄生回路失稳频率最高，远离制导控制系统频率；阻尼力矩和弹簧力矩隔离度寄生回路失稳频率相对降低，不断接近制导控制系统频率；而负的天线罩误差隔离度寄生回路失稳频率最低，与制导控制系统频率最为接近，这说明寄生回路对于负的天线罩误差斜率更加敏感且更容易失稳，这也从根本上解释了不同因素引起的隔离度寄生回路稳定域存在区别的原因.

图6表明，在相同的隔离度幅值Rdr=2.5%下，弹簧力矩与阻尼力矩隔离度寄生回路的时域响应相比无隔离度时均产生了一定程度的超调振荡，但基本保证了稳态增益不受影响；正的天线罩误差斜率引起的隔离度寄生回路时域特性较好，但是降低了稳态增益；而负的天线罩误差斜率引起的隔离度寄生回路时域特性最差，不仅产生了大幅度的振荡，同时稳态增益增加、收敛时间加长.

综上所述可知，弹簧力矩、阻尼力矩、正负天线罩误差斜率引起的隔离度均会恶化制导控制系统的稳定性，同时对系统时域响应产生较大影响，其中负的天线罩误差斜率影响最为剧烈，因此在雷达平台导引头的设计和测试中，应首先重点关注负的天线罩误差斜率引起的隔离度大小.

3 对制导精度的影响

导引头隔离度在影响制导控制系统稳定性的同时，也对导弹制导性能产生不利影响，这种影响主要体现在制导精度. 分别考虑雷达导引头噪声和目标随机机动输入下，导引头隔离度存在时对制导精度的影响. 雷达导引头噪声主要包括闪烁噪声、接收机热噪声和褪色噪声3种，这里仅以闪烁噪声为代表进行分析，其功率谱密度用ΦGN表示.

图7给出了不同干扰输入下的制导回路模型.

给定典型空空导弹参数N=4，vc/vm=2，τα/τg=4，定义MD为脱靶量，选取τF/τg=15，利用图7的伴随系统进行仿真. 图8和图9分别给出了闪烁噪声和目标随机机动输入下量纲一脱靶量随隔离度幅值变化曲线.

如图8所示可知，在隔离度寄生回路稳定的区域内，随着隔离度幅值Rdr的提高，弹簧力矩负的天线罩误差斜率和隔离度引起的脱靶量不断增大，阻尼力矩和正天线罩误差斜率隔离度引起的脱靶量反而略有减小；寄生回路失稳后，制导系统脱靶量迅速增加并趋于发散.

在相同的隔离度幅值下，对比来看，负的天线罩误差斜率隔离度引起的脱靶量最大，弹簧力矩和阻尼力矩隔离度引起的脱靶量依次降低，而正的天线罩误差斜率隔离度引起的脱靶量最小.

由图9所示可知，在隔离度寄生回路稳定的区域内，随着Rdr的提高，正的天线罩误差斜率隔离度引起的脱靶量不断增大，而弹簧力矩和阻尼力矩隔离度引起的脱靶量略有减小；同样，负的天线罩误差斜率隔离度引起的脱靶量在寄生回路失稳之前就已经发散. 在相同的隔离度幅值下，正、负天线罩误差斜率隔离度引起的脱靶量相对较大，而弹簧力矩和阻尼力矩隔离度引起的脱靶量相对较小.

以上分析表明，导引头隔离度会对导弹的制导精度产生不利影响，特别在寄生回路失稳以后，脱靶量迅速发散. 其中，负的天线罩误差斜率引起的隔离度对制导精度的影响最为严重.

4 基于UKF的在线补偿

导引头隔离度将对导弹制导控制系统的稳定性和制导精度产生严重影响. 通过设计一个UKF滤波器，可同时实现对弹簧力矩系数、阻尼力矩系数以及天线罩误差斜率的在线估计，将估计得到的真实视线角速度引入到制导系统中，可完成对导引头隔离度的实时在线补偿，降低隔离度对导弹制导控制系统的影响.

4.1 滤波模型的建立

为研究方便，令角速率陀螺传函Gg(s)=1，不考虑校正网络G1(s)和G2(s)，建立雷达平台导引头模型如图10所示.

由图10所示，选取滤波器状态变量为

X=

(6)

由此可列写状态方程为

(7)

其中，W(t)为系统随机输入白噪声，

W(t)=

[0w2(t)0000w7(t)w8(t)w9(t)]T；

其系统噪声方差阵记为Q；

(8)

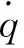
(9)

由此可列写量测方程为

(10)

其中，

(11)

V(t)=[v1(t)v2(t)v3(t)]T为零均值量测白噪声，其量测噪声方差阵记为RV.

由式(7)(11)可知，滤波器的状态方程与量测方程均呈非线性，因此不能直接使用线性卡尔曼滤波解决非线性系统的估计和滤波问题.UKF是一种适用于非线性系统状态估计的滤波方法，它基于UT变换，根据原状态分布的均值和方差，在其周围进行Sigma点采样，经滤波方程传播后利用加权求和产生变换后的均值和方差.

4.2 仿真验证

完成滤波模型的建立之后，将其引入到导弹制导回路模型当中，分别在初始速度指向误差和目标常值机动输入下，通过UKF算法完成对弹簧力矩系数、阻尼力矩系数以及天线罩误差斜率的实时在线估计，并使用估计得到解耦的真实视线角速度进行制导，以此抑制导引头隔离度对导弹制导控制系统的影响. 图11给出了引入UKF在线补偿算法的导弹制导系统模型框图.

由图11所示带有UKF在线补偿的制导回路进行仿真验证，制导时间tF=8 s，量测量噪声水平分别为σv1=0.3°，σv2=0.2(°)/s，σv3=0.3°. 弹体做振幅3°、频率2 Hz的正弦摆动. 其余仿真中所用制导控制系统参数由表2给出.

表2 制导控制系统仿真参数

在导弹飞行过程中，由于温度、气压等因素的影响，导引头内部工作环境相比于地面时将发生较大改变，因此导引头中弹簧力矩系数、阻尼力矩系数和天线罩误差斜率也会随之发生变化. 在这里为了更加贴合实际情况，同时考察算法对被估计参数变化的自适应性和鲁棒性，假设弹簧力矩系数Kn、阻尼力矩系数Kω及天线罩误差斜率Rφ随时间做小幅度的正弦变化，设置为

(12)

4.2.1 速度指向误差输入下补偿效果分析

给定初始速度指向误差ε=5°，由以上条件进行UKF在线补偿仿真，并与EKF方法进行对比. 图12给出了速度指向误差下UKF算法对弹簧力矩系数Kn、阻尼力矩系数Kω和天线罩误差斜率Rφ的估计结果.

由图12所示可知，UKF滤波器可以实现对弹簧力矩系数、阻尼力矩系数和天线罩误差斜率的一次性同时估计. 在整个导弹制导过程中，尽管被估参数随时间发生变化，UKF算法依然可以快速收敛，并且可以较为准确地跟踪被估参数的变化. 与EKF相比，UKF具有更高的估计精度以及更好的自适应性和鲁棒性.

图13给出了速度指向误差下UKF算法对弹目视线角速度的估计结果.

由图13可以看出，与EKF相比，UKF补偿算法可以更为准确地实现对真实弹目视线角速度的实时估计，基本上消除了隔离度对视线角速度的影响.

图14给出了速度指向误差下不同制导时间tF时有无UKF补偿算法对导弹脱靶量的影响.

由图14可知，在导引头隔离度的影响下，无补偿时，由于隔离度寄生回路已经失稳，导弹脱靶量无法收敛且已发散；而采取UKF补偿算法之后，可有效抑制导引头隔离度对脱靶量的影响，当末导时间tF>10τg时，导弹脱靶量基本可以收敛到无隔离度影响时的水平，很大程度上提高了制导精度. 相比于EKF，UKF对脱靶量的补偿效果要更好.

4.2.2 目标常值机动输入下补偿效果分析

给定目标常值机动为aT=6g进行UKF在线补偿仿真，并与EKF方法进行对比. 图15和图16给出了目标常值机动下UKF算法的估计结果.

由图15和图16可知，在目标常值机动输入下的整个制导过程中，相比于EKF，UKF算法依然可以更好地跟踪被估计参数的变化，并完成对弹目视线角速度的实时估计.

图17给出了目标常值机动下不同制导时间tF时有无UKF补偿算法对导弹脱靶量的影响.

由图17可知，在目标常值机动输入下，采取UKF补偿算法之后，消除了导弹脱靶量由寄生回路失稳引起的发散问题，导引头隔离度对脱靶量的影响得到了较好的抑制，但是补偿后的导弹脱靶量并没有完全收敛至无隔离度时的水平，补偿效果相比于速度指向误差输入时有一定差距. 相比于EKF，UKF算法对脱靶量的补偿效果依然要更好一些.

5 结 论

建立了包含天线罩误差的雷达导引头隔离度模型，对比分析了弹簧力矩、阻尼力矩和天线罩误差引起的隔离度寄生回路稳定性及其时域频域性能，并研究了其对脱靶量的影响，最后提出了一种基于UKF的隔离度在线补偿方法，得到以下结论：

① 对于雷达导引头来说，弹簧力矩、阻尼力矩及天线罩误差均会引起隔离度寄生回路，恶化制导控制系统稳定性，其中负的天线罩误差斜率影响最为严重，其次是弹簧力矩.

② 导引头隔离度会降低制导精度. 在闪烁噪声输入下，负天线罩误差斜率和弹簧力矩隔离度引起的脱靶量相对较大；而在目标随机机动输入下，正、负天线罩误差斜率隔离度引起脱靶量相对较大.

③ 所提出的基于UKF的隔离度在线补偿方法能够较为准确地同时估计出弹簧力矩系数、阻尼力矩系数和天线罩误差斜率，将估计得到的视线角速度引入到制导系统中，可实现对导引头隔离度的有效抑制，提高制导精度. 相比于EKF，UKF在线补偿算法具有更高的估计精度与更好的补偿效果.

[1] Kennedy P J， Kennedy R L. Direct versus indirect line of sight stabilization[J]. IEEE Transactions on Control Systems Technology， 2003，11(1):3-15.

[2] 王嘉鑫，林德福，祁载康，等.全捷联相控阵雷达导引头隔离度寄生回路研究[J].北京理工大学学报，2013，33(11):1124-1129.

Wang Jiaxin， Lin Defu， Qi Zaikang， et al. Study on disturbance rejection rate parasitical loop of strapdown phased array radar seeker[J]. Transactions of Beijing Institute of Technology， 2013，33(11):1124-1129. (in Chinese)

[3] Song Jianmei， Cai Gaohua. Precision analysis of the semi-strapdown homing guided system[C]∥Proceedings of AIAA Guidance， Navigation， and Control Conference. Minneapolis，Minnesota， USA: AIAA， 2012:1-14.

[4] 李富贵，夏群利，蔡春涛，等.导引头隔离度寄生回路稳定性及测试方法[J].北京理工大学学报，2013，33(8):801-805.

Li Fugui， Xia Qunli， Cai Chuntao， et al. Stability and measurement of seeker disturbance rejection rate parasitic loop[J]. Transaction of Beijing Institute of Technology， 2013，33(8):801-805. (in Chinese)

[5] 徐平，王伟，林德福.导引头隔离度对末制导炮弹制导控制的影响[J].弹道学报，2012，24(1):17-21.

Xu Ping， Wang Wei， Lin Defu. Effect of seeker isolation on guidance and control of terminal guided projectile[J]. Journal of Ballistics， 2012，24(1):17-21. (in Chinese)

[6] 宋韬，林德福，王江.平台导引头隔离度对导弹制导系统影响[J].哈尔滨工程大学学报，2013，34(10):1234-1241.

Song Tao， Lin Defu， Wang Jiang. Influence of seeker disturbance rejection rate on missile guidance system[J]. Journal of Harbin Engineering University， 2013，34(10):1234-1241. (in Chinese)

[7] Masten M K. Application of control theory to design of line-of-sight stabilization system[C]∥Proceedings of American Control Conference. Boston， MA: IEEE， 1985:1219-1222.

[8] Song T L， Shin S J. Active homing performance enhancement with multiple model radome slope estimation[C]∥Proceedings of AIAA Guidance， Navigation， and Control Conference and Exhibit. Providence， Rhode Island， USA: AIAA， 2004:931-940.

[9] Cao X R， Dong C Y， Wang Q， et al. Improvement of homing missile guidance performance using fuzzy adaptive IMM radome slope estimation[C]∥Proceedings of the 2009 2nd International Congress on Image and Signal Processing. Tianjin， China: IEEE， 2009:1-5.

[10] Lin C L， Hsiao Y H. Adaptive feedforward control for disturbance rejection in seeker stabilizing loop[J]. IEEE Transactions on Control Systems Technology， 2001，9(1):108-121.

[11] 徐娇，王江，宋韬，等.基于扰动观测器的导引头隔离度抑制方法研究[J].兵工学报，2014，35(11):1790-1798.

Xu Jiao， Wang Jiang， Song Tao， et al. A distur-bance observer-based inhibition method for distur-bance rejection rate of seeker[J]. Acta Armamentarii， 2014，35(11):1790-1798. (in Chinese)

(责任编辑：刘雨)

Influence of Radar Seeker Disturbance Rejection Rate with Radome Error and On-Line Compensation with UKF

ZONG Rui1， LIN De-fu1， LAN Ling2， WANG Hui1

(1.School of Aerospace Engineering， Beijing Institute of Technology， Beijing 100081， China;2.Beijing Xinfeng Machinery & Equipment Co. ， Ltd. of CASIC， Beijing 100854， China)

For the heavy impacts of radar seeker disturbance rejection rate on missile guidance and control system， a disturbance rejection rate model of radar seeker was established considering radome error. The stability and time-frequency domain performance of parasitic loop caused by spring torque， damping torque and radome error were comparatively analyzed based on the model. Analyzing the relationship between miss distance and disturbance rejection rate under different interferences， an on-line compensation method was proposed with unscented Kalman filter (UKF)， and was validated with simulation. The research results show that， the disturbance rejection rate of radar seeker can weaken the stability and guidance accuracy of the guidance system， and the infection of negative radome error slope is the most serious. With glint noise， miss distance caused by negative radome error slope and spring torque is larger， while with random target maneuver， the miss distance caused by positive and negative radome error slope is larger. The UKF on-line compensation method can estimate the coefficient of spring torque and damping torque and the radome error slope with velocity pointing error and constant target maneuver. The disturbance rejection rate can be controlled effectively， the stability and performance of guidance system are improved with the compensation.

radar seeker; radome error; disturbance rejection rate parasitic loop; unscented Kalman filter(UKF); on-line compensation

2015-04-13

国家自然科学基金资助项目(61172182)

宗睿(1988—)，男，博士生，E-mail：zongrui1988@163.com.

TJ 765.4

A

1001-0645(2016)12-1269-10

10.15918/j.tbit1001-0645.2016.12.012