具有迟滞特性的水下小车牵引系统控制方法

　， ， 　， 　(.华中科技大学 船舶与海洋工程学院， 湖北 武汉　430074；.武汉船用机械有限责任公司， 湖北 武汉　430074)

引言

水下液压绞车由于其工作效率高，负载能力强、密封问题易于解决，而被广泛应用于水下驱动，但液压系统存在迟滞特性及参数时变性，给其的精确速度控制带来不小的困难[1]。

图1为某水下液压绞车牵引小车的示意图，小车长5 m，宽1.2 m，高3.5 m，牵引绞车由50 kN液压马达驱动，通过钢丝绳牵引小车在长48 m的水下导轨上作往复间隙运动，导轮1和导轮2起到改变钢丝绳运动方向及施加张紧力的作用，绞车滚筒为单层滚筒，两根牵引钢缆固定在滚筒中间，牵引小车时，钢缆从滚筒两端收放缆。

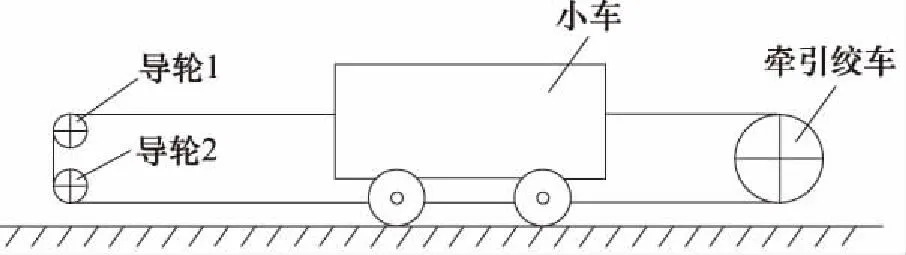
图1　水下液压绞车牵引小车示意图

经过前期试验得出，电液比例阀响应控制指令有约1 s迟延；液压系统由4台泵联合供油，管路较多，且主阀阀芯至液压马达间的管路长达50 m，液压绞车对于阀芯开度的响应存在约3 s迟滞，即本液压系统存在迟滞特性，总迟滞时间约4 s。迟滞特性会引起系统超调，加上整个柔性牵引系统刚度不足，小车牵引系统出现失稳，小车速度出现震荡。同时液压系统参数随着油温变化，负载随速度变化，这进一步增加系统的非线性及参数时变性，给较高精度的速度控制带来了难度。常规的Smith预估补偿器能够较好的控制纯滞后对象，但对系统模型精度要求较高，针对液压系统的迟滞性及参数时变性，提出了一种基于改进Smith预估补偿器的模糊PID算法，在改进Smith预估补偿器的基础上，加入模糊控制策略，实现了对液压绞车牵引小车速度的高精度控制。

1　小车速度控制系统建模

水下小车速度控制原理图如图2所示，小车速度控制器根据速度的设定值及速度反馈值，通过调节电液比例阀的阀芯开度，控制液压绞车的运动速度，进而调节液压绞车牵引小车的运动速度。

图2　小车速度控制原理图

1.1　液压绞车模型[2]

阀的线性化流量方程：

QL=Kqxv-KcpL

(1)

连续性方程：

(2)

力矩平衡方程：

(3)

联立可得马达转角速度对阀位移的传递函数：

(4)

各参数定义及选用数值，见表1[3]：

综合上述数据可得：

阀控马达系统固有频率：

(5)

液压阻尼比：

(6)

马达转角速度对阀位移的传递函数为：

(7)

由于液压绞车对于阀芯开度有3 s的响应迟滞，故液压绞车对于阀芯开度的传递函数具有迟滞环节：

(8)

1.2　电液比例阀模型

为了便于分析，将电液比例阀增益设定为1，考虑电液比例阀响应控制指令有约1 s的迟滞，电液比例阀传递函数为：

P(s)=1×e-s=e-s

(9)

1.3　小车模型

为便于分析，将液压绞车与小车的柔性连接方式简化为刚性连接，即不考虑钢丝绳的弹性对牵引系统所带来的影响。考虑绞车驱动小车运动时，由于小车质量较大所带来的惯性环节，设定小车模型为：

(10)

1.4　速度传感器模型

将速度传感器简化为比例环节，传递函数为：

K(s)=1.5

(11)

1.5　系统稳定性分析

将各环节传递函数代入图2，水下小车速度控制系统方框图可描述如图3所示。

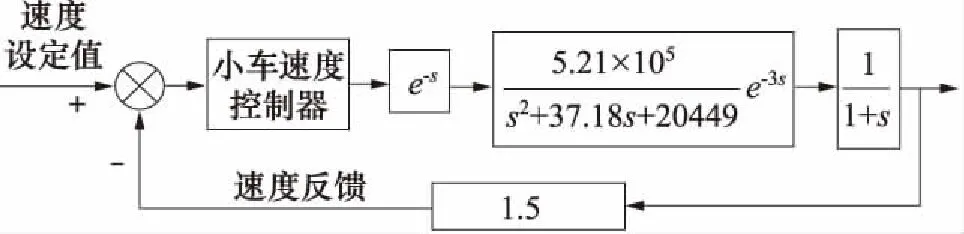
图3　小车速度控制系统框图

由上图可知，小车速度控制系统的前向通道传递函数可简化为：

存在迟滞环节，可利用MATLAB程序画出其开环Bode图。为了便于对比，分别绘制了速度控制系统考虑迟滞环节和不考虑迟滞环节的Bode图(如图4)，不考虑迟滞环节的Bode图，其幅值裕度为1.4621 dB，相位裕度为89.3382°，系统稳定；而考虑迟滞环节后，系统幅值裕度为1.0672 dB，相位裕度为55.0402°，系统稳定，但较不带迟滞环节系统其幅值稳定储备较小，处于临界稳定状态。可见由于迟滞环节的存在， 会导致系统不稳定，小车速度控制系统考虑迟滞环节的特性并加以矫正，才能稳定地工作。

图4　有延迟环节的Bode图

图5　无延迟环节的Bode图

2　Smith预估算法

2.1　常规Smith预估补偿算法

纯滞后环节的存在使系统的相位出现滞后，随着滞后时间的增加，相位滞后增加，系统的稳定性降低，导致控制质量下降，Smith预估补偿算法为提高这类系统的稳定性，在调节器的两端反向并联一个反馈补偿网络，结构如图6所示[4]。

图6　常规Smith预估补偿算法结构图

在图6中，G0(s)代表被控对象中不含纯滞后部分的传递函数，e-τs代表被控对象的纯滞后部分，Gc0(s)代表控制器的传递函数，Gm(s)代表对象模型中不含纯滞后部分的传递函数，e-τms代表对象模型纯滞后部分。

其中,G0(s)=Gm(s)，τ=τm

图7为对无迟滞环节进行PID控制(曲线2)与对带迟滞环节进行Smith控制(曲线3)的对比曲线。仿真结果表明，无迟滞环节系统稳定，PID控制器能够实现较好的控制效果；带迟滞环节系统由于采用了Smith预估补偿算法，控制结果较无迟滞环节系统仅会将整个控制过程在时间轴上向后推移，而不会对控制结果产生影响。从图中也可看出，曲线3为曲线2在时间轴上后移了4 s的迟滞时间。

图7　无迟滞环节PID控制与带迟滞环节Smith控制

图8为对迟滞环节分别采用PID控制(曲线2)和常规Smith预估算法控制(曲线3)的对比曲线，常规Smith预估算法控制曲线具有较快的响应时间和稳定时间，而PID控制曲线则响应效果较差。由1.5节系统稳定性分析可知，带迟滞环节系统幅值稳定储备较小，处于临界稳定状态，故在PID控制只能减小系统增益来换取系统的稳定性；若为了加快控制系统的相应速度而增大系统增益，则会使系统失稳，振荡。

图8　带迟滞环节PID控制与常规Smith控制

2.2　改进的Smith预估补偿算法

由上节可知，常规Smith预估补偿在迟滞环节系统中有较好的应用，但该补偿算法对建模精度要求较高，模型失配会对控制结果造成影响，针对其对模型误差敏感的缺点， C.C.Hang等提出了改进的Smith预估器,其原理如图9所示[5]。

图9　改进Smith预估补偿器结构图

如图9所示，改进Smith预估补偿器传递函数为：

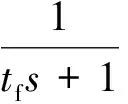
结合企业践行绿色发展理念的实际举措，颜泽彬表示，去年以来，华星化工紧紧围绕创新、协调、绿色、开放、共享五大发展理念，紧扣国家经济由高速增长向高质发展转变的主基调，确定了“去瓶颈、补短板、谋发展”总体工作思路，扎实推动公司各项工作不断取得新突破。

1) 增益K变化

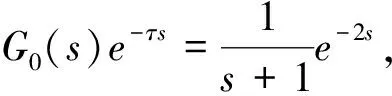
图10　增益K变化

2) 时间常数T

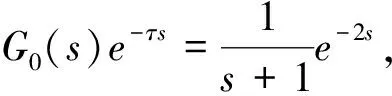
3) 时滞常数τ

图11　时间常数T变化

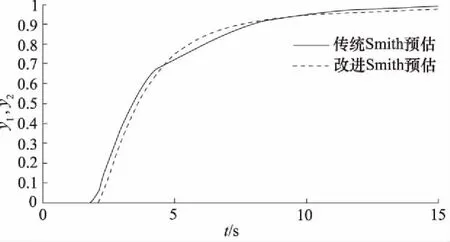
图12　时滞常数τ变化

综合上述数字仿真可见，改进Smith预估补偿算法较常规Smith预估补偿算法有较好的模型自适应性。

2.3　基于改进Smith预估补偿的模糊PID控制

改进Smith预估补偿原则上可以改善大滞后系统的控制品质，并对迟滞系统模型具有一定的模型自适应性，但由于PID控制器也是基于被控对象的精确数学模型而设计的，因而对于缺乏精确模型或参数时变的纯滞后过程控制难以获得满意的控制效果。水下液压绞车是一种典型的大滞后、变负载非线性系统，系统的参数随负载、油温的变化而随时变化，因而所建立的数学模型不可能很精确，所以单独采用改进Smith预估控制有很大的局限性。

模糊控制器具有鲁棒性强的特点，能够在较大的范围内自动适应被控对象参数的变化，因而无需被控对象的精确数学模型。从模糊控制原理上讲，单纯的模糊控制难以有效解决对于具有较大时间滞后对象的控制问题，而在模糊控制系统中引入改进Smith预估补偿，能够充分发挥模糊自适应控制和Smith预估补偿的优点，有效提高模糊控制器对具有纯时间滞后对象的控制能力，如图13所示。

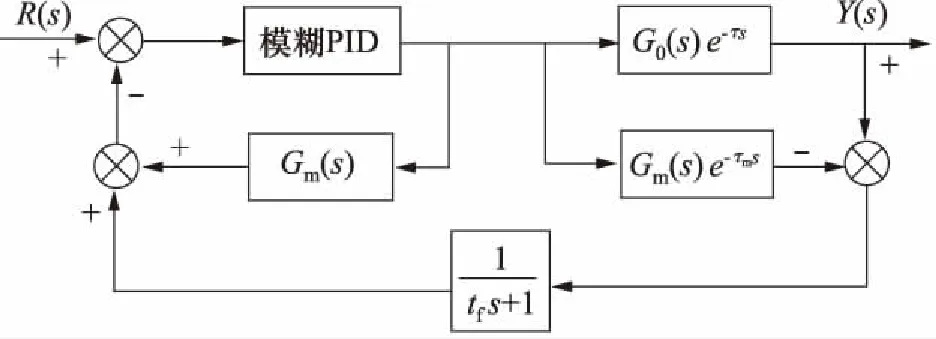
图13　改进Smith预估补偿的模糊PID控制

模糊PID控制器找出误差e和误差变化量ec与PID参数控制参数之间的模糊关系，在控制过程中，实时监控e和ec的数值，根据模糊规则控制表对三个控制参数进行在线调整，而对控制对象模型精度要求不高，具有一定的模型自适应性。模糊自适应PID控制原理图如图14所示。

图14　模糊自适应PID控制原理图

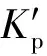
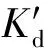
(12)

PID 参数控制规则见表2～表4[6]：

表2　ΔKp控制规则表

表3　ΔKi控制规则表

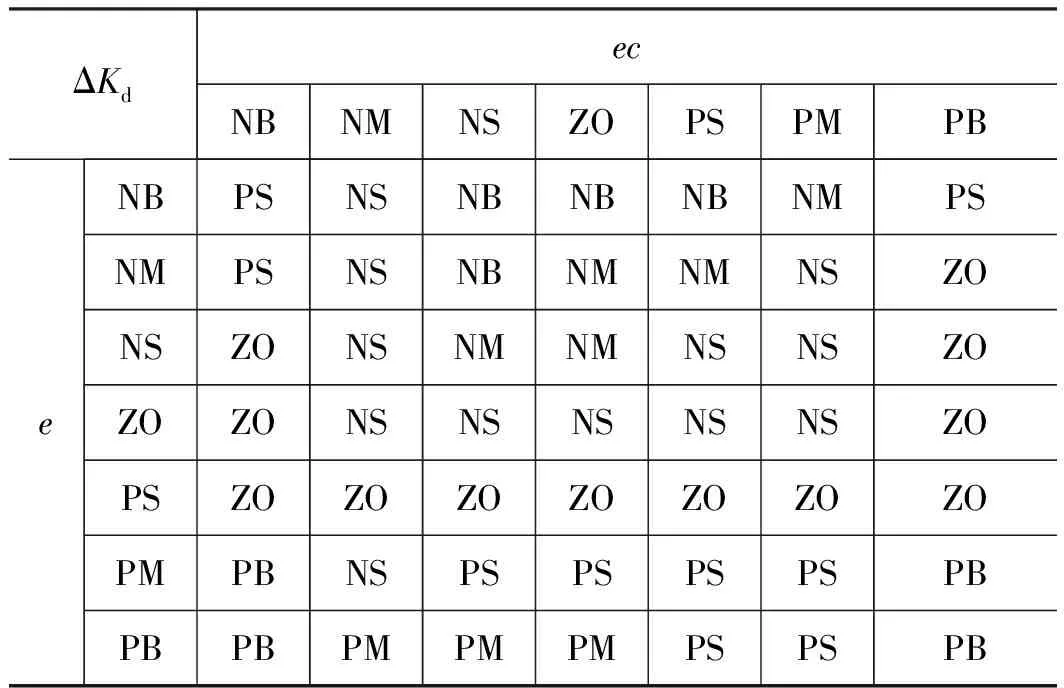
表4　ΔKd控制规则表

3　数学仿真及结果分析

图15中对带迟滞环节的模型失配系统分别使用常规Smith预估算法(曲线2)，改进Smith预估算法(曲线3)和基于改进Smith预估算法的模糊PID控制(曲线4)的数学仿真图。三种控制算法均能使系统稳定，但在控制效果上有所差异： 常规Smith预估控制器由于对于控制建模精度要求较高， 在模型失配的情况下需要有较长的稳定及调整时间；基于改进Smith预估补偿的PID控制器能够较为理想的克服迟滞环节和模型失配对控制所带来的影响，控制效果较好；基于改进Smith预估补偿的模糊PID控制器则具有较快的响应时间及较小的超调量，控制效果最佳。

图15　MATLAB数学仿真图

4　结论

(1) 对水下液压绞车进行数学建模，并利用MATLAB绘制控制系统Bode图，迟滞环节会给控制系统带来不稳定性，给精确控制带来挑战；

(2) 常规Smith 预估校正能够较好解决控制通路给通道中迟滞环节带来的影响，但对建模精度要求较高；改进Smith预估校正则具有较好的模型自适应能力；

(3) 针对水下液压绞车模型时变的特点，利用基于改进Smith预估校正的模糊PID控制器，对液压绞车牵引小车进行速度控制，控制效果较好。

参考文献：

[1]赵亮.液压提升机电液比例伺服系统研究[D].徐州:中国矿业大学，2011.

[2]曾志林,徐国华,赵寅,徐兵.水下大负载高精度液压绞车滑模控制研究[J].液压与气动,2012,(7):18-20.

[3]李祖佳. 水下平台及其驱动绞车控制研究[D].武汉:华中科技大学，2011.

[4]陈宇杰.时滞系统的Smith预估控制研究[D].杭州：浙江大学, 2006.

[5]Hang C C, Astrom K J A.New Smith Predictor for Controlling a Process with an Integrator and Long Dead-Time[J].IEEE Transactions on Automatic Control, 1994, 39(2):343-345.

[6]Zhi-Wei Woo, Hung-Yuan Chung. A PID Type Fuzzy Controller with Self-tuning Scaling Factors [J].Fuzzy Sets and Systems,2000，(115)：321-326.