基于直方图对无损数据隐藏的立体图像编码

童学锋，李书萌，沈广策，宣国荣

（同济大学 电子与信息工程学院，上海201804）

作为无损数据隐藏的应用，基于无损数据隐藏的立体图像编码是将无损数据隐藏和3D电视两个前沿研究结合起来，将立体图像的一幅（左图）压缩后，无损嵌入另一幅（右图）中，使得3D电视的传输和存储容量减少一半，同时大大增加了灵活性（3D与2D电视兼容的可能）.从2007年开始，文献［1-4］对该方向进行研究，随着3D电视逐渐推广，基于无损数据隐藏的立体图像编码日益得到重视，从近年论文来看，已经接近实用化程度.立体图像的二幅图像中一幅无损恢复，另一幅（左图）近似无损恢复，峰值信噪比 PSNR（peak signal to noise ratio）达到40 dB以上（一般36dB以上时肉眼已经很难看出压缩数据变化的存在）.本文对以往的方法做了改进，取得了很好的效果.

立体图像利用人类左右眼所看到图像的差异，通过水平放置、位置略有差异的一组相机同步获得左右两幅图像，来构成立体图对，人眼通过同步处理两幅图像的信息来感知场景深度，更具有真实感.然而，由于立体图像是由两幅图像组成的，它的存储空间和传输带宽是单幅图像的两倍.一个解决问题的直接方法是将两幅图像各自压缩，但是这种方法没有利用到图像间的相关性，效果并不理想.

为了更好地降低立体图像的尺寸，同时保持图像的可见性，在以往的工作中进行了一些关于高效压缩的研究［1-4］.在最新的进展中，大部分工作集中在视差估计方面.视差就是从有一定距离的两个点上观察同一个目标所产生的方向差异，在本方面的研究中，被看做一张图像中的一个点与另一张图像中对应点之间偏移的像素距离.利用视差估计，可以对立体图像进行编码.

基于无损数据隐藏的立体图像编码基本的方法是用立体图像中的一张作为参照图（右图），利用图像间的相关性和视差估计，将非参照图（左图）有损压缩后，无损嵌入到参照图中.由此可以只存储和传输一张图像，且保持了图像的可见性，节省了频带，便于管理.

由于在压缩相关信息时，采用了有损压缩，因此提高重建图像的质量，主要取决于两个方面：所采用的数据隐藏算法的嵌入极限容量和压缩后相关信息的质量.如果相关信息能够被完全嵌入到参照图中，非参照图就能够被无损还原.但由于嵌入容量的限制，在嵌入前需要对相关信息做有损压缩.即通过重建立体图像，可以无损恢复参照图，近似恢复非参照图.提高重建图像的质量，提高非参照图（左图）重建的PSNR，是本文的技术关键.

在文 献 ［3］的 方 法 中，使 用 SAD（sum of absolute differences）算法对参照图中的所有像素建立其在非参照图中的相应点，由相应点间的距离获得密集视差图，根据视差图计算得到残差矩阵后，对于矩阵中的大量负数，文献［3］采用了将所有像素值加255除以2的方法，但使用这种方法会产生不可逆的失真，影响重建图像的质量.文献［4］提出了减少不可逆失真的新计算方法，将图像均分为16×16的非重叠块，计算每一块整体视差并记录，从而减小需要记录的数据量.对于残差矩阵中负数问题，分情况采用两种处理方法：如果残差中最大值加最小值的绝对值小于255，则将每个像素加上残差中的最小值，否则采用文献［3］的方法.

文献［3-4］的方法都会在计算残差过程中产生失真，且需要嵌入的数据量大.本文方法中，首先由SAD算法计算出密集视差图，由于视差图具有区域特征，将其划分为相同大小的非重叠块，对每块内的视差值取众数（出现次数最多的值）或取均值，构成较小的视差图，从而降低数据量，且保持一定精度.根据此视差图求得的残差矩阵，其像素值范围是［-255，+255］，不能用JPEG 2000（Joint Photographic Experts Group，组织的图像压缩标准）直接压缩，需要进行预处理使其范围转换为［0，+255］，从而作为图像进行JPEG 2000有损压缩.范围转换通常是有损的，而本文采用无损范围转换.

此外，记录在预处理过程中超出范围的像素点的位置，将此记录信息和视差图、压缩后的残差图一起嵌入到参照图中.本文采用文献［5］的基于直方图对的无损数据隐藏方法，不仅能够提高嵌入率，而且嵌入数据后的图像具有更好的视觉效果.

1 立体图像编码方法

本文提出的基于直方图对无损数据隐藏的立体图像编码和解码方法如图1所示.在本文中，将立体图对中的右图R作为参照图，将左右图的相关信息计算后嵌入到右图中，重建后的左图记为L′，目前的研究就是要提高L′的重建质量.

本文中用到的变量如下：L与R分别代表立体图对中的左右图，W×H指图像大小，w为匹配窗口系数，S为视差搜索范围，D（x，y）为密集视差图，［m，n］为密集视差图分块系数，D（i，j）为分块压缩后的视差图，r为残差矩阵，r′为预处理后的残差图，Q为JPEG 2000压缩系数，rc为压缩后的残差图，R′为嵌入信息后的右图，rm为解压缩后的残差图，r′m为解压缩后的残差矩阵，L′为重建的左图.

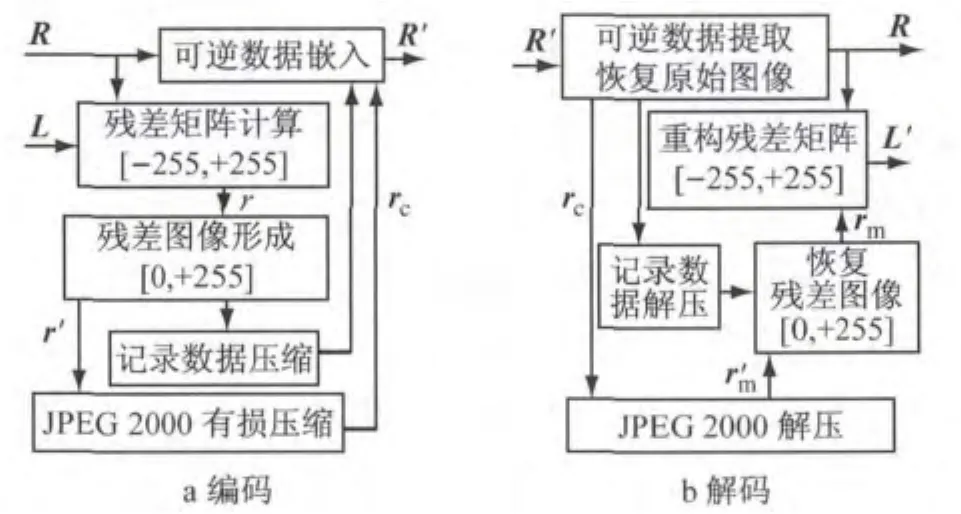
图1 立体图像的编码与解码流程图Fig.1 Flowchart of proposed stereo image coding

1.1 相关信息计算

1.1.1 视差计算

本文采用的视差估计算法是把左图L中某个像素点的邻域作为匹配基元，在右图R中搜索相似的对应点邻域，从而实现两幅图像的匹配并得到密集视差图.在搜索过程中，采用SAD算法作为两个搜索区域的相似性衡量.

SAD算法是一种广泛应用于图像匹配的算法，其基本流程为：在某个像素点的邻域构造一个固定范围的小窗口，用窗口分别覆盖左图L和右图R，左边覆盖区域减去右边覆盖区域，求出所有像素点差值的绝对值的和.对右图R的窗口做一个像素距离的向左平移，再次计算绝对差值和，重复平移和计算的过程（设定一个搜索范围S，在［1，S］的范围内平移窗口）.找到使SAD值最小的窗口，即找到了左图L的最佳匹配的像素点，此时平移的像素距离即为该点的视差值，在边缘处若找不到最佳匹配点，则令其视差值为0.设匹配窗口的大小为（2w+1）×（2w+1），该算法用如下公式表示：

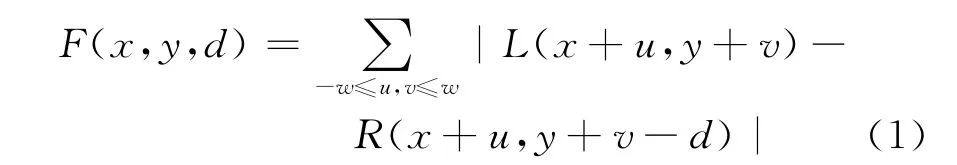
式中：（x，y）为像素点的坐标，以F表示当前平移量d下计算的绝对差值和.

在计算过程中，可以根据重建图像的PSNR大小修改w和S的值，以得到最佳效果.由SAD算法进行匹配，得到像素点（x，y）的视差值为

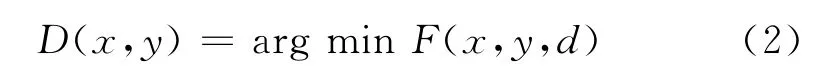
此时所有像素点的视差值构成立体图对视差图D（x，y），称之为密集视差图，大小为W×H，与原图像大小相同，数据量略大.本文根据密集视差图的区域特征（区域之间有一定的界限、区域内部有明显的相似性和连续性）将其划分为m×n大小的非重叠块（所有块的集合为整幅图像），取块内均值，得到压缩后的视差图D（i，j），大小为I×J（I=W／m，J=H／n）.分块平均法能够有效提高重建左图的质量，详细分析如下：

（1）视差和视差图的定义.立体图像的两幅图像对应点的纵坐标一致，横坐标有异，横坐标的差值就是该点的视差值.立体图像的左图（待压缩的图像）的每一个像素，与右图（参照图）对应点的视差，形成左图的视差图，简称视差图.

（2）密集视差图.由公式（1）和（2），在规定窗口系数w和视差范围S的基础上，计算SAD，获得视差值，每个像素点的视差值形成密集视差图.

（3）分块平均法的目的.分块平均是为了取得近似于真实的视差图.密集视差图受到图像本身内容影响，起伏太大，并不能完全等于真实的视差图.本文将密集视差图分块平均，由于小块内部的相似性和连续性，分块平均法可以取得近似于真实的视差图，记为D（i，j）.

（4）分块平均法的过程.首先划分为m×n大小的非重叠块，然后取每块的平均值.实际上在每小块中取均值时，有时考虑众数（一组数据中，出现次数最多的数就称为这组数据的众数）效果会更好.考虑众数的方法是，如果众数的出现频率大于1／4，则取众数作为该块的整体视差值，否则取该块所有视差值的平均值.由此可以得到更小的视差图D（i，j）.

（5）分块平均法的分析.分块平均法的作用是在提高视差图真实性的基础上，压缩视差图数据量.在同样最大嵌入容量限制的条件下，降低有损压缩率，最终提高重建左图的质量，得到更高的PSNR.对于分块m×n=8×8时，视差图数据量可以降低到原始密集视差图的1／64.考虑到分块前后视差图均可以预先压缩，实际可以降低到原始密集视差图的1／30～1／20.

（6）分块平均法的检验.以立体图对的左图重建效果为例，分块m×n=8×8时，PSNR=47.15 dB.如果其他参数不变，用密集视差图，即分块m×n=1×1时，PSNR=41.94dB以下.其他参数不变，分块用全图，即m×n=384×288时，PSNR=44.41 dB.可见适当分块能明显提高PSNR，达到最优PSNR的峰值.

1.1.2 残差矩阵计算

公式（2）建立了L（x，y）和R（x，y-D（i，j））之间的关系.其中，D（i，j）为像素点（x，y）所在第i行第j列小块的整体视差值.由此能够对左图L的像素值做出估计，即L′（x，y）=R（x，y-D（i，j））.对于不能均分的图像，从左上角开始划分，留出边缘部分，使左右图直接相减来计算残差.最终得到残差矩阵r（x，y）=L（x，y）-L′（x，y）.

由此可见，根据L′和r，左图L可以无损恢复，即将压缩后视差图D（i，j）和残差矩阵r嵌入右图，就可以在提取信息后重建左图.但由于无损数据隐藏的嵌入容量限制，需要对数据进行有损压缩才能够完全嵌入，因此不能无损恢复左图，本文研究的目的正是为了提高左图重建的质量.

1.2 压缩方法

残差矩阵的数据是相关信息中的主要数据.本文采用JPEG 2000的编码方法对其压缩，但原始残差矩阵的范围在［-255，+255］，不能作为图像进行编码.根据残差矩阵直方图的分布特点，对其进行预处理，如图2所示.首先将所有像素点的残差值加上128，然后对于超出［0，+255］范围的值，分别以0和+255为轴线作轴对称变换，使其处于［0，+255］的范围内，可视为一张残差图像.公式表示如下：

对于r（i，j）＜-128和r（i，j）＞+127的像素点，记录其位置（i，j），采用这种方法可以消除残差预处理时造成的失真，且需要记录的数据量很小.恢复残差矩阵的方法为

本文的残差预处理方法可以实现对左图的无损恢复，然而对于无损数据隐藏来说，嵌入量一般约在0～2.5bpp（bit per pixel）之间.而残差图的大小是大于2.5bpp的，所以需要对残差图进行有损压缩.本文采用的是JPEG 2000压缩方法，压缩率记为Q.

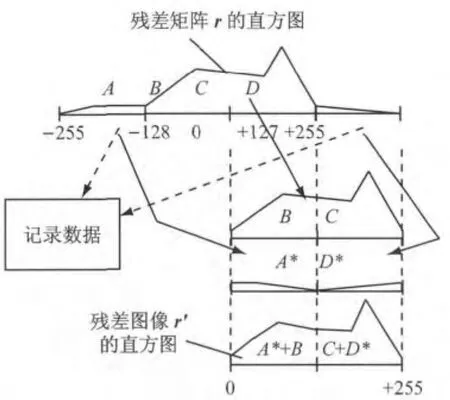
图2 由视差矩阵形成视差图像的示意图Fig.2 Formation of residual error image by residual error matrix

1.3 最优解

采用本文方法重建图像过程中，可以通过调整以下参数来获得最优的重建效果，使PSNR最大.

（1）SAD匹配窗口大小（2w+1）×（2w+1）：对于每一个像素点，其视差值与周围的局部小区域相关，若搜索窗口过大，相关性减弱，甚至会得到错误的匹配结果，不同图像的最优匹配窗口大小因其像素相关性而异.

（2）视差搜索范围S：S是指每个像素点的SAD窗口平移的像素距离范围，S值过小则搜索不到最优解，过大则会把视差无关的信息包含进来，造成效果下降.由于物体距离观察点远近不同，造成图像中所在区域的视差不同，各个图像的最优视差搜索范围也不同.本文根据重建图像的PSNR来调整S的取值，使每一个像素点的视差值尽量取与其真实对应点距离相同或相近的值，提高残差矩阵为0的个数，减少相关信息数据量，因此可在JPEG 2000有损压缩的压缩率低的情况下嵌入，从而降低失真，提高重建图像的质量.

（3）视差分块大小m×n：密集视差图是有区域特征的，由于视差值的连续性，对每块取众数或均值可以保持视差估计的精确度，同时又减少需要嵌入的数据量.分块过大时，连续性弱，该块的视差值不具有代表性；分块过小，数据量太大，不利于嵌入.密集视差图区域内部的相似性和连续性决定了最优视差分块的大小.在实际操作中，除整张图作为一块的实验外，总有m=n.

（4）JPEG 2000的压缩率Q：当Q值较小时，压缩率低，失真小，左图重建PSNR高；当Q值较大时，压缩率高，失真大，左图重建PSNR低.但低压缩率会造成需要嵌入的数据量大，而无损数据隐藏方法是有嵌入率限制的，因此需要在嵌入率极限内寻找能使PSNR最高的Q值.不同图像的最优率取决于其相关信息数据量和极限嵌入率的大小.

以上参数都因图像而异，具体取值需要根据左图重建的PSNR来调整，以达到最优解，即

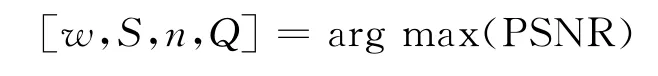
2 基于直方图对的无损数据隐藏方法

本文数据隐藏是采用文献［5-6］中基于直方图对的数据隐藏方法.该方法不仅能够嵌入大量数据，而且嵌入后的图像具有非常好的视觉效果.下面简单介绍直方图对方法：在一幅灰度图像中，灰度值为x的像素点出现的频度可以用直方图h（x）表示，如果两个相邻的灰度值满足［h（x）=m，h（x+1）=0］或［h（x）=0，h（x+1）=m］，则称（x，x+1）构成一个直方图对.如果直方图中本身没有直方图对，则需通过扩展来形成.在形成直方图对的过程中可能发生灰度值溢出的问题.为预防这一问题发生，在扩展前先对边界区的像素点进行调整，使其远离边界区，令直方图分布变窄.

在该方法中，使用嵌入阈值T表示在何处开始形成直方图对，TL和TR分别表示对左、右边界区的像素点调整的范围.该方法基本流程如下，举一个简单的例子（见图3）：设嵌入阈值T=6，TL=0，TR=1（像素值超出6称为溢出），需要嵌入的数据为D=［1，0，0，1］.

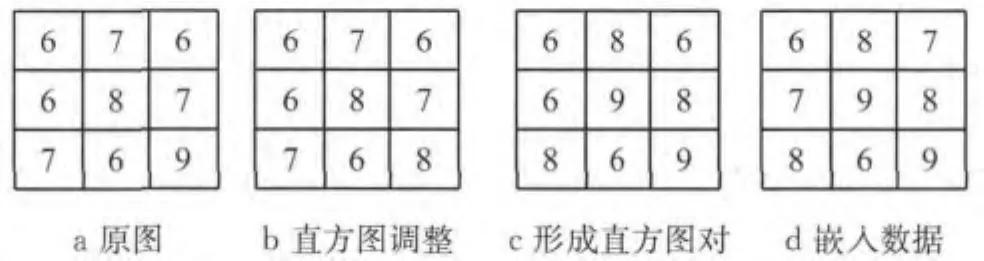
图3 直方图对数据隐藏实例Fig.3 An example of histogram-pair based data hiding

第1步 原始图像，直方图［h（6），h（7），h（8），h（9）］=［4，3，1，1］；

第2步 直方图调整（TL=0，TR=1）［h（6），h（7），h（8），h（9）］=［4，3，2，0］；

第3步 形成直方图对，［h（6），h（7），h（8），h（9）］=［4，0，3，2］，［h（6），h（7）］= ［4，0］；

第4步 在阈值T=6处嵌入数据D=［1，0，0，1］后，［h（6），h（7），h（8），h（9）］= ［2，2，3，2］，直方图对变成［h（6），h（7）］=［2，2］.

由于需要嵌入的数据量略大，在嵌入时对直方图对方法做了改进，即采用多循环分次嵌入来提高嵌入容量.本文使用的实验图像来源于标准立体图像库，由于本文是在以往论文方法上的改进，为便于与以往效果比较，选取图像Ⅰ（Tsukuba，384×288）、图像Ⅱ（Venus，434×383）和图像Ⅲ（Baby，413×370）作为实验图像，如图4～6所示.

图4 图像Ⅰ原始立体图像Fig.4 Original stereo image of PictureⅠ

图5 图像Ⅱ原始立体图像Fig.5 Original stereo image of PictureⅡ

图6 图像Ⅲ原始立体图像Fig.6 Original stereo image of PictureⅢ

本文对图像Ⅰ，Ⅱ，Ⅲ的右图嵌入数据时，嵌入量和嵌入效果PSNR的大小变化见表1.当嵌入量增大时，嵌入效果随之降低.

文献［3-4］的嵌入方法为文献［7］的数据隐藏方法，与本文使用的文献［5］的嵌入方法对比见图7.

3 立体图像重建

如图1所示，立体图像编码后，在传输过程中图像是可见的，接收端可以通过解码获得立体图对，从而得到立体信息.解码步骤如下：① 使用文献［5］的方法提取数据，得到压缩后的残差图rc、记录的信息、压缩后视差图D（i，j），以及无损恢复的右图R；② 使用JPEG 2000解码方法对残差图解压缩，再根据记录信息进行处理得到残差矩阵r′m；③ 利用残差矩阵和视差图重建左图L′，即可得到立体图对.

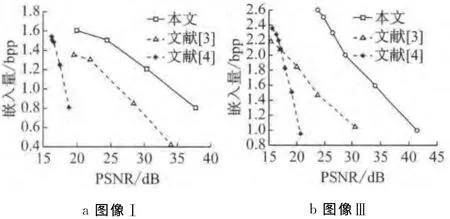
图7 基于直方图对的可逆数据隐藏与其他嵌入方法比较Fig.7 Comparison of histogram-pair based reversible data hiding with other data hiding schemes

表1 直方图对数据隐藏方法嵌入后图像PSNRTab.1 PSNR of image embedded by histogrampair based data hiding

4 实验结果

对图像Ⅰ，Ⅱ，Ⅲ反复试验，可以得到PSNR最优解.需要嵌入的信息包括压缩后视差图与压缩后的残差图以及记录信息.本文采用SAD算法应用于图像计算出的视差图如图8所示.

由于此时3幅图像的嵌入量分别为1.37，0.94和0.63bpp，如果直接嵌入，数据量略大.本文采用对m×n小块取众数或均值压缩图像的方法，图像压缩后嵌入量分别降为0.049，0.032和0.031bpp，可以直接嵌入，将压缩后图像放大后如图9所示.

计算残差矩阵时，对每个像素点使用该点所在小块的视差值进行计算，对于某些图像中由于不能均分未能计算出视差的边缘部分（如图像Ⅲ（413×370）不能均分为10×10小块），令该部分的左右图像直接相减.原始残差矩阵的像素值范围是［-255，+255］，进行处理使之在［0，+255］范围内，以便JPEG 2000有损压缩，处理后的残差图见图10.

图8 密集视差图Fig.8 Dense disparity

图9 压缩后视差图Fig.9 Compressed disparity

图10 残差图Fig.10 Residual error

此时，需要记录的像素点数量因图像而异，图像Ⅰ为44个，图像Ⅱ为96个，图像Ⅲ为0个.记录每个点所在的位置，记录信息的数据量分别为0.021，0.018和0bpp，可以直接嵌入.

在对残差做有损压缩的情况下，为了得到更好的重建图像质量，应使有损压缩的压缩率尽可能小，也即无损数据隐藏技术能够嵌入的数据量应尽可能大.本文中图像Ⅰ残差图的JPEG 2000压缩率为5.1，嵌入数据量为1.60bpp，重建的左图为47.15 dB，嵌入后右图的PSNR值为20.01dB，如图11所示.图像Ⅱ的JPEG 2000压缩率为4.5，嵌入数据量为1.80bpp，重建的左图为47.15dB，嵌入后右图的PSNR值为27.1dB，如图12所示.图像Ⅲ的JPEG 2000压缩率为3.1，嵌入数据量为2.59bpp，重建的左图PSNR值为52.65dB，嵌入后的右图为23.72 dB，如图13所示.

图11 图像Ⅰ立体图像编码效果Fig.11 Stereo image coding results of PictureⅠ

当嵌入量比较大时，嵌入后的右图有比较严重的失真，但是根据无损数据隐藏的特点，如果在图像的传输或保存中没有损失的情况下，依然能够无损获得右图和因JPEG 2000压缩而有损的左图，因此，使用本文的方法解码后可以获得高品质的立体图像.而且，如图14所示，使用本文的嵌入方法，嵌入量更高，重建左图的效果更好.

图12 图像Ⅱ立体图像编码效果Fig.12 Stereo image coding results of PictureⅡ

图13 图像Ⅲ立体图像编码效果Fig.13 Stereo image coding results of PictureⅢ

图14 不同嵌入量重建左图的效果对比Fig.14 Result comparisons of reconstructed left image with different payloads

表2是在不同参数下搜索得到的最优PSNR.可见采用本文的方法相对于以前的方法，重建左图PSNR以及嵌入后右图PSNR都较高.

表2 本文最优PSNR及与其他方法比较Tab.2 Comparison of optimal PSNR of proposed method with other methods

5 结论

（1）文献［4］的方法是一次选择，设定非重叠块的大小和搜索范围，得到降低尺寸的视差图，即得到块内最优视差值.本文的方法是二次选择，首先采用文献［3］的匹配窗口和搜索范围的方法，得到点最优视差值，形成密集视差图，再将各像素点视差值在块内取众数或取均值.由于二次选择选取了更多参数的最优值，因此能够达到更高的PSNR.

（2）文献［3］的方法得到的密集视差图数据量大，进行了JPEG 2000有损压缩造成失真.本文对密集视差图压缩后能够直接嵌入，可以无损恢复.

（3）本文提出新的视差处理方法与残差预处理方法，能够使相关信息在压缩前无损，通过调整匹配窗口大小系数、视差搜索范围、视差分块系数、JPEG 2000压缩率等参数，使相关信息更准确、需要嵌入的数据量更少，从而使重建图像的质量更高，能够得到最优的PSNR.

（4）本文采用文献［5］的直方图对无损数据隐藏方法来嵌入信息，比以往使用的文献［7］的方法，嵌入率更大，视觉效果更好.

实验结果证明，与以往的立体图像编码方法相比，本文方法重建出的左侧图像PSNR提高3dB以上.

［1］ Coltuc D.On stereo embedding by reversible watermarking［C］∥Signals，Circuits and Systems.Iasi：IEEE，2007：1-4.

［2］ Coltuc D.Improved capacity reversible watermarking［C］∥Image Processing.San Antonio：IEEE，2007：III-249-III-252.

［3］ Coltuc D， Caciula I.Stereo embedding by reversible watermarking：Further results ［C］∥ Signals，Circuits and Systems.Iasi：IEEE，2009：1-4.

［4］ Chen H.An effective stereo image coding method with reversible watermarking ［J］.Journal of Computational Information Systems，2012，8（7）：2761.

［5］ XUAN Guorong，TONG Xuefeng，TENG Jianzhong，etal.Optimal histogram-pair and prediction-error based image reversible data hiding［C］∥ Digital Forensics and Watermaking.Heidelberg：Springer Berlin Heidelberg，2013：368-383.

［6］ XUAN Guorong，SHI Yunqing，CHAI Peiqi，etal.Optimum histogram pair based image lossless data embedding［C］∥Transactions on Data Hiding and Multimedia Security IV.Heidelberg：Springer Berlin Heidelberg，2009：84-102.

［7］ Tian J.Reversible data embedding using a difference expansion［J］.IEEE Transactions on Circuits &Systems for Video Technology，2003，13（8）：890.