面向液力变矩器负载的泵轮动态转矩估计模型
2015-04-16王安麟章明犬
王安麟,章明犬,郭 威
(同济大学 机械与能源工程学院,上海201804)
液力变矩器作为车辆性能匹配的关键部件,其最大作用在于确保能量和动力平滑高效地从发动机传到变速器乃至轮胎,因此其性能表现对整机动力性、经济性等都有重大影响[1].在复杂恶劣工况条件下,工程机械车辆装备在波动载荷作用下行驶过程中频繁启制动,其对整机传动系统要求更为苛刻,因此对工程机械用液力变矩器动态特性进行研究将对整机性能改善有重要意义.
液力变矩器泵轮直接与发动机相连以实现变矩器与发动机合理匹配,其转矩波动对发动机油耗及动力输出产生巨大影响.目前国内外对变矩器研究主要包括变矩器影响因素分析及优化[2],变矩器内部流场及耦合分析[3],以及变矩器静动态特性分析等[4-5].其中泵轮转矩波动规律通过变矩器动态特性分析得到,目前动态特性研究主要包括理论研究与实验研究两方面[6-7]:对动态特性理论研究通过建立变矩器状态空间模型及线性系统辨识得到系统参数及其特性;对动态特性试验研究主要通过变矩器台架实验模拟车辆起制动、换挡等工况揭示其特性.这两方面研究尚存在的缺陷在于:基于流体动力学建立的系统状态方程未考虑变矩器强非线性特征;试验研究虽能反映真实特性,但动态特性试验施加的边界条件不明确且施加困难;两者缺陷的本质原因在于没有液力变矩器特性与整机波动载荷关联性研究理论的指导.但文献[8-9]的研究结果分别表明等效参数、流场特性等都随速比、扭矩的变化而改变,因此有必要联系整机作业工况展开液力变矩器动态特性研究.
为了揭示单级三元件液力变矩器泵轮转矩动态表达,本文在综合分析液力变矩器泵轮转矩波动对整机性能影响基础上,从变矩器质量弹簧阻尼系统模型和一元束流理论模型推导结果对比中,提出泵轮转矩的载荷波动项概念;通过控制变量法开展CFD(计算流体动力学)仿真试验,得到考虑负载特征的泵轮动态转矩估计模型.经过全面仿真试验结果与计算值对比,表明模型准确性.该估计模型能更真实地揭示复杂恶劣工况下变矩器与发动机的匹配情况,为整机实现液力变矩器在初始配置设计中与发动机的动态性能匹配提供依据.
1 理论分析
1.1 发动机与变矩器匹配中的特性分层现象
整机在工作过程中,转速、负荷总处在波动中,当外界波动经过变速器、液力变矩器等传到发动机曲轴上,将直接影响发动机动力输出以及整机性能.如图1a表明了发动机与液力变矩器的外特性匹配,液力变矩器不同速比下的特性曲线簇与发动机外特性曲线交点即为额定工况匹配点.
实际整机工作过程中,往往是发动机输出轴扭矩先于转速发生改变,因此可假设某一时刻转速不变,扭矩会出现波动.故当阻力矩比较稳定的情况下,两者工作在额定工况附近,发动机输出功率波动较小,大部分时间输出最大功率;当阻力矩波动剧烈时,易造成特性分层:如图1a中由a1点到a2点即在不同油耗曲线之间变动,由图1b中可看出在转矩大或转速大情况下油耗较大且变化趋势较陡,故a1点到a2点变动直接增加发动机油耗;由b1点到b2点即在不同功率曲线之间变动易于造成实际输出功率降低,即功率利用不足;由c1点到c2点即由额定工况点附近到超负荷运行,此时司机往往来不及反应调整铲刀角度,极有可能导致发动机冒黑烟甚至熄火.
从上述分析可知:与液力变矩器泵轮直接相连的发动机输出轴转矩波动对整机的动力性、经济性有很大影响,转矩波动过大将对发动机适应性提出更高要求.在整机对液力变矩器的初始选配设计时,必须考虑泵轮转矩的波动性,以实现液力变矩器与发动机的动态特性匹配,因此有必要对泵轮转矩波动性展开研究.

图1 发动机与液力变矩器匹配特性Fig.1 Match characteristics of engine and torque converter
1.2 液力变矩器的静态特性分析
装载机常用二级双涡轮液力变矩器,其工作原理一般是在低速重载时两个涡轮同时工作,高速轻载时第二涡轮单独工作;装载机整机功率损失较为严重一般发生在低速重载情况下,因此研究低速重载时的泵轮转矩情况更有价值;在低速重载时二级双涡轮液力变矩器实质是按单级三元件液力变矩器原理工作的;故作为研究对象而言,单级三元件液力变矩器便能反映出本质问题.常用的单级三元件液力变矩器主要由泵轮、涡轮和导轮组成,它可根据涡轮轴上的外载荷大小自动、无级地进行变速、变矩.一般认为:液力变矩器的性能主要通过静态特性参数效率、起动转矩比来表示

式中:η和K分别为变矩器的效率和转矩比;TP,ωP和TT,ωT分别为泵轮扭矩、转速和涡轮的扭矩、转速.对于此次研究所选用的液力变矩器,由CFD仿真得到静态特性,如图2所示.由图2可看出,液力变矩器效率最大即最佳工况点在传动比0.7附近,且其最高效率可达到80%左右;起动转矩比可达到2左右.由特性曲线表明,该液力变矩器具有较好的静态特性,能代表一般单级三元件液力变矩器静态特性特征,另一方面也表明此研究模型的广泛适用性.

图2 单级三元件液力变矩器静态特性Fig.2 Static characteristics of single stage three elements torque converter
对于液力变矩器泵轮转矩大小研究主要是基于各种转速比条件下的稳态试验,以得到转矩系数随速比变化曲线,最终得到液力变矩器泵轮转矩的静态表达式为

式中:TP,0为泵轮静态转矩;λP(i)为泵轮转矩系数,它是速比i的函数,如图2;ρ,g分别为油液密度和重力加速度;D为变矩器的有效直径.由式(3)可以看出:当泵轮转速不变的情况下,对于确定结构的液力变矩器,其泵轮扭矩与扭矩系数成线性关系.
液力变矩器泵轮转矩的静态表达能够符合传统工程机械传动系统研究要求,但变矩器作为一种液力传动装置,相较传统齿轮、连杆等传动方式有其自身的特点:①有很强的可变刚性,能减小载荷波动对传动系统的损害;②阻尼不定性,较大的阻尼对整机有很好的缓冲减振作用,但不同转速下阻尼大小不同.液力变矩器有着强非线性特征,故基于静态实验的泵轮转矩的简单线性表达无法在泵轮轴上反映出外载荷的波动性.
基于上述特点及现代整机对元部件更高的设计要求,为实现变矩器与发动机和变速器更合理的匹配,有必要探究变矩器泵轮转矩更精确的表达.在泵轮转速不变、外载波动的情况下,液力变矩器实际泵轮扭矩特征可通过CFD仿真得到.设定泵轮转速为2 000r·min-1,速比为0.7,涡轮转速波动幅值为140r·min-1,频率20Hz情况下,变矩器泵涡轮转速、转矩输出如图3所示.
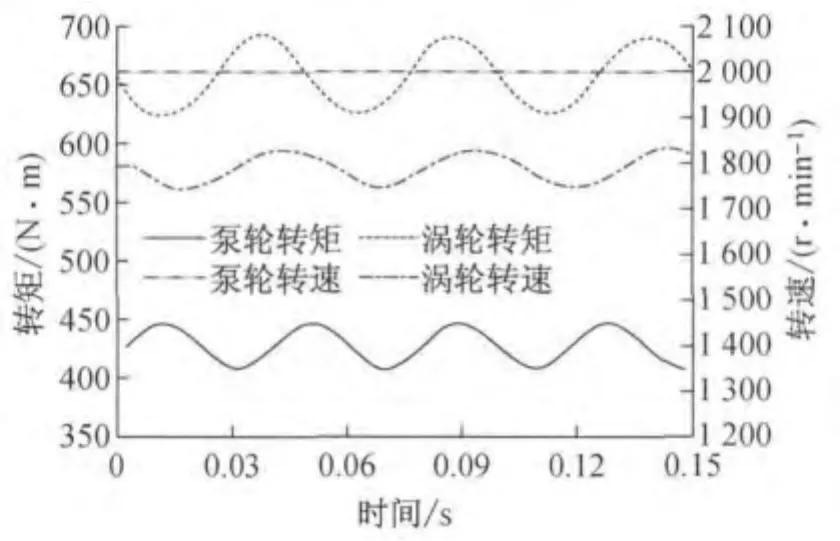
图3 转速、扭矩仿真结果对比Fig.3 Contrast between simulation results of speed and torque
由图3转速波动曲线与扭矩波动曲线对比可知,在泵轮转速保持不变,涡轮转速定幅值波动的条件下,泵涡轮扭矩也相应出现波动,但扭矩变化明显出现延时,且泵轮扭矩波动幅值相对涡轮扭矩波动幅值有所衰减.这种延时性的转矩波动特征是无法通过泵轮转矩静态表达式表现出来的,它反映了变矩器的非线性.
类似仿真试验的这种外载荷、速度波动造成液力变矩器泵涡轮扭矩波动现象在变矩器实验中也有所反映,如文献[10]中的图3-11揭示了汽车液力变矩器泵涡轮扭矩波动情况.由于工程机械工况恶劣,载荷波动大,泵轮扭矩波动会更剧烈,因此有必要从理论与实验方面探讨泵轮动态转矩的影响因素以及映射关系.
1.3 泵轮动态转矩理论分析
1.3.1 基于质量弹簧阻尼系统模型推导泵轮动态转矩
由上述液力变矩器与发动机匹配分析过程可知:对于某种确定结构、确定型号的变矩器,当作为传动系统关键部件组装到工程机械整机时,所关心的是在整机转速、载荷波动传到变矩器涡轮轴时,经过变矩器对发动机输出轴转矩波动幅值的影响,故可以忽略内部结构因素,从液力变矩器输入输出量的角度加以考虑.
由液力变矩器传动原理以及液压油动力传输特点,可将液力变矩器简化为典型的质量弹簧阻尼系统.即将变矩器泵涡轮转速、扭矩作为输入输出的外部条件,将该液力传动系统简化为变阻尼、变刚度的二阶振动系统.其具体示意图见图4[11].

图4 质量弹簧阻尼系统模型示意图Fig.4 Schematic model of mass-spring damping system
据此可建立液力变矩器传动的数学模型,具体表达式如下[11]
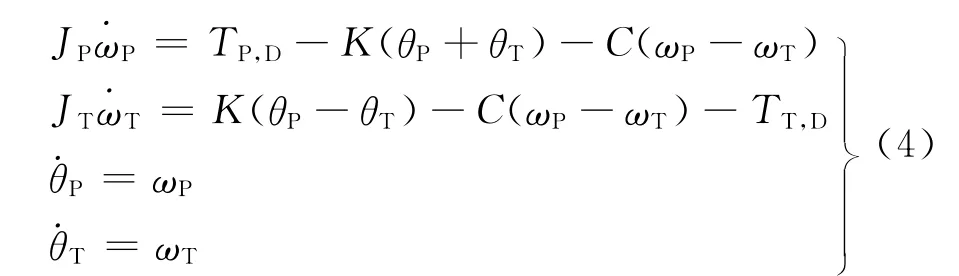
式中:JP,JT分别 为泵轮、涡 轮的转 动惯量;TP,D,TT,D分别为泵轮、涡轮的动态转矩;θP,θT分别为泵轮、涡轮的旋转角位移;K,C分别为变矩器的刚度和阻尼.考虑到液力传动系统变阻尼、变刚度的传动特性,即K=K(i),C=C(i),在泵轮转速基本保持不变的条件下K=K(ωT),C=C(ωT)且dωP/dt=0,据此根据该液力传动系统表达式(4)可推导如下泵轮动态转矩的微分表达式:

由于某一瞬间泵涡轮角位移基本不变,考虑到具体液力变矩器某种工况下的阻尼、刚度都与涡轮转速有关,可得到泵轮动态转矩的模糊表达为
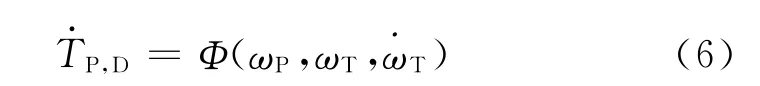
因此基于变矩器的质量弹簧阻尼系统模型可推导出泵轮动态转矩的波动幅值ΔTP,D模糊表达为

式中:ΔTP,D为泵轮转矩波动幅值;ΔωT为涡轮转速波动幅值;Φ为函数映射关系.式(7)表明依据质量弹簧阻尼系统模型推导出泵轮转矩波动幅值与泵涡轮转速、涡轮转速波动幅值有关.
1.3.2 基于一元束流理论推导泵轮动态转矩
在流体动力学理论基础上,工程应用中常根据一元束流理论设计改进液力变矩器.因此,基于一元束流理论的三点假设,可以推导得到波动载荷条件下变矩器泵轮的动态转矩[1]
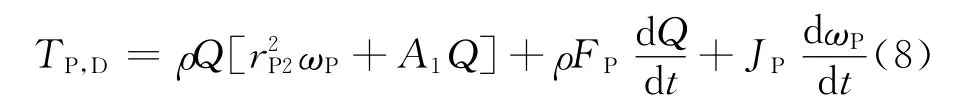
式中:Q,rP分别为循环流量和泵轮有效半径;A1为泵轮综合几何参数;FP为泵轮叶片流道的几何参数形状因素.对式(8)中的结构参数和确定常数量分别用A,B,C,D代替,式(8)即可简化为

从函数关系角度来看,TP,D可以得到一种复合式的隐函数表达,即

由于泵轮转速基本保持不变,故dωP/dt=0,流量Q的微分表达为
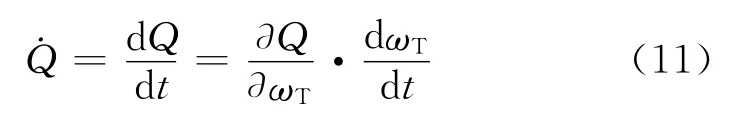
根据复合函数求导法则,结合式(9)对TP,D求导,即
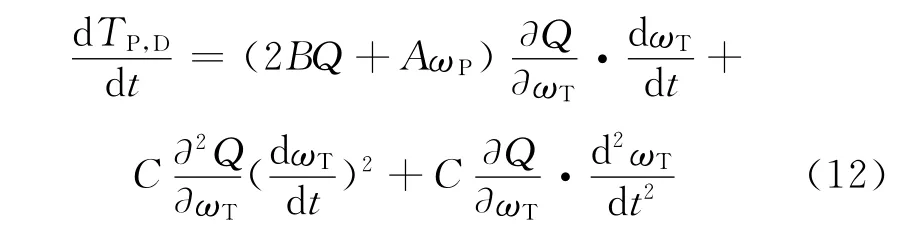
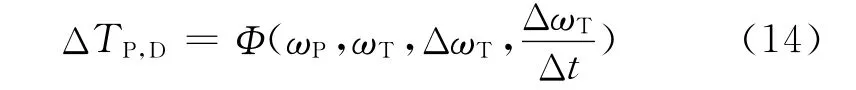
由式(14)与式(7)对比可知:与质量弹簧阻尼系统模型相比,基于一元束流理论推导出的泵轮转矩波动幅值的模糊表达多一个影响参量ΔωT/Δt.这种分析结果说明在表达液力变矩器内在机理方面,一元束流理论相较质量弹簧阻尼系统模型更全面;液力变矩器内在复杂流场所导致的转矩波动已远远超出简单质量弹簧阻尼系统模型所能刻画的范畴.
1.3.3 泵轮动态转矩的载荷波动项概念提出
由式(3)液力变矩器泵轮转矩的静态表达可知:对于确定结构的液力变矩器,其泵轮转矩只与泵涡轮的转速有关,这明显未考虑整机外载荷波动对泵轮转矩的影响.由式(14)对于泵轮转矩波动幅值的模糊表达的影响参量来看,ΔωT/Δt表示涡轮转速变化的快慢,即涡轮转速变化的角加速度.这说明即使两个液力变矩器模型在某一时刻泵轮、涡轮的转速相同,但涡轮的角加速度不同时,其泵轮对应的转矩值应是不同的.这从理论上说明了泵轮转矩静态表达模型是不准确的.
再者,ΔωT/Δt为角加速度项,这反映的是整机的载荷特征,即式(14)为液力变矩器泵轮转矩的载荷波动项.这说明实际泵轮转矩的波动性与整机类型及其工况是紧密关联的.对于汽车、装载机以及推
忽略结构参数及常量,为探求变矩器泵轮转矩波动的影响因素,基于函数映射关系从式(12)可总结出下式:
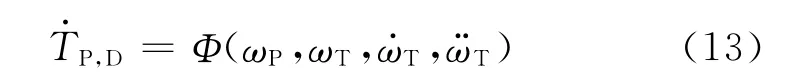
据此,可以得到较为精确的泵轮动态转矩波动幅值ΔTP,D的表达式为土机等,由于工况条件的不同,其各自对应的泵轮转矩的载荷波动项是不同的.由式(14)可知,液力变矩器泵轮动态转矩的载荷波动项模型可用图5表示.

图5 泵轮动态扭矩载荷波动项模型Fig.5 Load fluctuation model of pump wheel dynamic torque
2 仿真实验
2.1 控制变量法仿真试验研究
由式(14)知,对于确定结构的液力变矩器,其关联负载特征的泵轮动态转矩载荷波动项与泵涡轮转速、涡轮转速波动幅值以及涡轮转速波动快慢有关.为探究各参数对泵轮转矩载荷波动项的影响,本文基于流体动力学原理,应用CFD软件进行分析,即对单级三元件液力变矩器建立全流道三维仿真模型,选择六面体网格单元和标准的k-ε湍流模型,设定各叶轮流道进口速度边界和出口压力边界,进行液力变矩器内流场的数值模拟计算.
实际仿真试验方法采用控制变量法进行,即每组试验变化一个参数,其他参数保持不变,以此防止各参数间相互影响.因此若仅使ΔωT/Δt变化,ΔωT恒定,则变为研究泵轮转矩波动幅值随频率f=1/Δt的影响,且由i=ωT/ωP,式(14)即变为

以ωP,ωT,ΔωT,f为自变量,ΔTP,D为因变量开展仿真试验.在实际CFD仿真过程中,为保证模型是由稳态过渡到涡轮转速以某一幅值波动状态,先必须确定某一恒定的泵轮和涡轮转速,进行稳态流体解析求出稳态收敛解;然后保持泵轮转速不变,涡轮转速值在稳态设定值基础上加上正弦波动项进行瞬态解析.其仿真过程中具体输入、输出转速设定情况如图6所示.

图6 CFD仿真过程泵涡轮转速设置Fig.6 Pump turbine speed settings in CFD simulation process
在载荷波动项解析过程中设定泵轮转速为ωP,0,涡轮转速设定分为两个阶段:t1阶段转速为ωT,0,t2阶段转速为ωT,D.其中ωT,D的表达式如下:
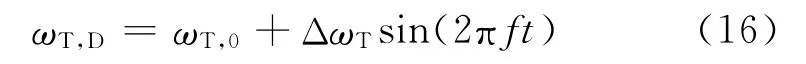
每次仿真试验中变化式(15)中的某一自变量,其他变量保持基准值,即泵轮转速为2 000r·min-1,速比为0.7,涡轮转速波动幅值、频率分别为140r·min-1,20Hz,结果输出泵轮动态转矩的载荷波动项幅值.多组仿真后得到的离散值,经最小二乘法拟合得到曲线如图7所示.

图7 控制变量法仿真结果曲线图Fig.7 Simulation results based on control variable method
由图7可知:在泵轮转速恒定条件下,单级三元件液力变矩器泵轮动态转矩的载荷波动项幅值与泵轮转速、涡轮转速波动幅值成正比关系,与涡轮转速变化频率近似成反比关系,与速比近似成指数变化关系.由此可总结ΔTP,D随wP,i,ΔwT,f变化关系的表达式为

其中,ξ为待定系数,其值与具体液力变矩器结构有关,可由实际变矩器仿真结果标定其值.该研究所用变矩器ξ值可标定为3.2×10-3.
2.2 全面仿真试验验证
为了验证泵轮动态转矩的载荷波动项表达模型的准确性,有必要进行多组仿真试验.在保证试验模型、仿真流程以及其他基本条件不变的情况下,仅要求参量wP,i,ΔwT,f分别取3个值,代表其值水平的低、中、高,构成81种组合,具体设定值如表1,开展CFD全面仿真试验求得其泵轮动态转矩的载荷波动项幅值.

表1 全面仿真试验各参变量取值Tab.1 Value of each variable in comprehensive simulation

图8 扭转波动幅值全面仿真结果与模型计算值线性回归分析Fig.8 Torque fluctuation amplitude linear regression analysis of comprehensive simulation results and calculated value of the model

图9 全面仿真结果与模型计算值的相对误差Fig.9 Relative error between comprehensive simulation results and calculated value of the model
将全面仿真试验结果与式(17)对应的泵轮动态转矩载荷波动项模型计算值进行线性回归分析,结果如图8所示,其线性回归系数为0.91,因此两者具有较好的线性相关性.仿真结果与模型计算值的相对误差如图9所示,其相对误差最大为4.6%,处在泵轮动态转矩载荷波动项幅值较小点附近;当泵轮扭矩波动幅值较大时,其相对误差最大在2%左右.综合分析可知:该泵轮动态转矩载荷波动项表达模型较为准确,适用性也较好.
2.3 结果
基于泵轮转矩的静态表达式,综合考虑上述分析研究的泵轮动态转矩载荷波动项表达模型,故实际面向液力变矩器负载特征的泵轮动态转矩估计模型为

式中TP,0,ΔTP,D的表达如式(3)和式(17),代入可确定整机载荷波动下变矩器泵轮动态转矩估计模型如下:
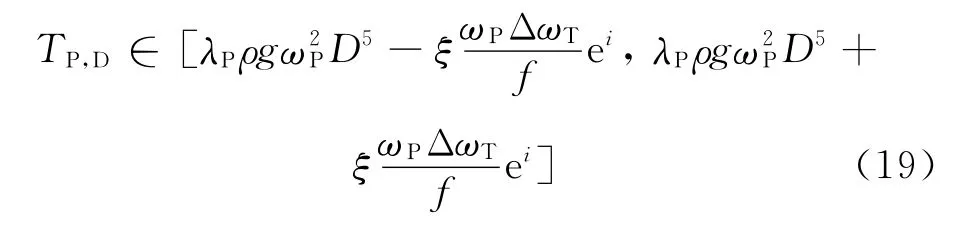
该泵轮动态转矩估计模型更加体现的是在考虑载荷波动情况下整个工作区间内的平均综合匹配性能,根据该模型得到的匹配方案相较传统静态匹配更加全面准确,也更符合工程实际.
2.4 实例应用
考虑载荷特征的液力变矩器泵轮动态转矩估计模型的应用主要体现在整机与变矩器的初始匹配设计中.当确定整机机型、工况条件的情况下,为整机初始选配液力变矩器时往往考虑的是发动机与液力变矩器的静态匹配,这种选配方式只考虑到发动机与变矩器之间的动力传递,实现整机主体零部件的匹配协调.这种设计理念并未将整体主机机型、外界载荷条件等考虑在内,导致的后果往往是静态匹配很好,但实际遇到复杂恶劣工况时,整机的性能却很差.
面向液力变矩器负载特征的泵轮动态转矩估计模型考虑到整机外载荷频率特征、波动幅度等,应用该估计模型在整机初始选配设计中能更真实反映在载荷波动情况下,发动机与变矩器的匹配效果.如图10a和b,选用的是同一型号发动机经过试验后得到的外特性曲线,以及两种型号的液力变矩器在理想额定工况下的外特性曲线.由泵轮的静态特性与发动机外特性的交点对比可知:图a中的变矩器取得最大转矩、最小油耗以及较高的输出功率,其静态特性匹配比图b中的液力变矩器匹配效果更好.现选定该液力变矩器用于装载机,考虑装载机载荷特征及传动系统传动比分配情况,载荷截止频率定为20 Hz,涡轮转速波动幅值100r·min-1,其泵轮动态转矩估计模型如两条细虚线所示,泵轮转矩处于上边界和下边界特性曲线区间之内,其与发动机的匹配性考虑的是整个区间内平均值:相较图a而言,图b中泵轮转矩在估计区间内有更高的平均转矩和平均输出功率,且更低的平均油耗.
因此,考虑载荷情况的泵轮动态转矩估计模型能更真实地揭示发动机与变矩器的实际匹配效果,对整机与变矩器的初始选配设计有较好的指导作用.

图10 两种液力变矩器与同一型号发动机特性匹配比较Fig.10 Feature matching contrast between two kinds of hydraulic torque converter with the same type of engine
3 结论
通过发动机与液力变矩器外特性匹配分析,揭示泵轮转矩波动会造成特性分层现象.通过CFD仿真结果以及文献[10]中的试验数据,表明现有泵轮转矩静态模型表达不准确.在对液力变矩器现有模型分析基础上,得出一元束流理论模型比质量弹簧阻尼系统模型更为准确,其泵轮动态转矩考虑了液力变矩器的载荷特征(ΔωT/Δt),以此提出液力变矩器泵轮转矩模型的载荷波动项概念.通过基于控制变量法的载荷波动项解析,与全面CFD仿真试验结果的比较,得到了面向液力变矩器负载特征的泵轮动态转矩估计模型并证明了其有效性.在对同一型号发动机与不同液力变矩器的静动态不同匹配结果的对比中,泵轮动态转矩估计模型考虑了整机机型、外载荷特征,能更全面揭示整机作业时发动机与液力变矩器的平均匹配效果.该估计模型对液力变矩器在关联整机负载特征的初始配置设计中具有更全面的指导作用.
[1] Kim B S,Ha S B,Lim W S,etal.Performance estimation model of a torque converter part I:Correlation between the internal flow field and energy loss coefficient[J].International Journal of Automotive Technology,2008,9(2):141.
[2] Asl H A,Azad N L,McPhee J.Math-based modeling and parametric sensitivity analysis of torque converter performance characteristics[R].Detroit:SAE World Congress,2011.
[3] Bai L,Fiebig M,Mitra N K.Numerical analysis of turbulent flow in fluid couplings[J].Journal of Fluids Engineering,1997,119(3):569.
[4] Brad P.Transient torque converter performance,testing,simulation and reverse engineering[J].SAE Transactions,2003,112(6):201.
[5] Dong Y,Lakshminarayana B,Maddock D.Steady and unsteady flow field at pump and turbine exit of a torque converter[J].Journal of Fluid Engineering,1998,120(3):538.
[6] Manea A,Dobanda E V,Babic M J.Theoretical and experimental studies on torque[J].Thermal Science,2010,14:231.
[7] Dong Y,Lakshminarayama B.Experimental investigation of the flow field in a automotive torque converter stator[J].Journal of Fluids Engineering,1999,121(4):788.
[8] 吴光强,王立军.基于CFD的液力变矩器等效参数性能预测模型[J].同济大学学报:自然科学版,2013,41(1):121.WU Guangqiang,WANG Lijun.CFD analysis-based torque converter performance prediction model with equivalent parameters[J].Journal of Tongji University:Natural Science,2013,41(1):121.
[9] 闫清东,邹波,魏巍.液力变矩-减速装置制动特性流场分析[J].吉林大学学报:工学版,2012,42(1):91.YAN Qingdong,ZOU Bo,WEI Wei.Numerical investigation of brake performance of hydrodynamic tractor-retarder assembly[J].Journal of Jilin University:Engineering and Technology Edition,2012,42(1):91.
[10] 张高峰.液力变矩器瞬态特性的实验研究[D].上海:上海交通大学,2012.ZHANG Gaofeng.Experimental study of torque converter transient characteristics[D].Shanghai:Shanghai Jiao Tong University,2012.
[11] CHEN Dongsheng,XIANG Changle,LIU Hui.Analysis and experimental identification of torsional dynamic characteristics of hydrodynamic torque converter[J].Journal of Beijing Institute of Technology,2002,11(2):150.
