路基不均匀沉降对车辆和轨道动力响应的影响

张小会，周顺华，宫全美，杨新文

（同济大学 道路与交通工程教育部重点实验室，上海201804）

在我国已建或规划的铁路线路中，无砟轨道线路占有相当大的比例，而板式无砟轨道由于其具有稳定性好、平稳性高及维修性优良等特点，逐步成为其轨道结构选择的主流模式.目前，我国板式无砟轨道主要修建于隧道内、桩基础和复合地基基础之上，土建成本巨大.关于在土质路基上修建板式无砟轨道的研究尚处于起步阶段，其技术难点在于在部分地区，特别是软土地区，板式无砟轨道由于受到周边荷载环境变化的影响，不可避免地出现路基不均匀沉降的情况，直接影响列车的运行安全和舒适性.因此确定合理的路基不均匀沉降限值是其亟需解决的问题之一.然而现有的无砟轨道规范中路基不均匀沉降限值的制定主要基于无砟轨道结构强度设计理论，并未考虑路基不均匀沉降对于系统动力响应的影响，而其动力响应将直接影响列车的运行安全性、乘客舒适性以及相关结构部件的损耗.

大量学者对路基不均匀沉降影响系统动力响应的问题进行了研究.Hunt［1］对路桥过渡段处不均匀沉降形式进行了研究，得到了过渡段处路基不均匀沉降对轮轨力和扣件力的影响.蔡成标等［2］通过建立列车-路基上板式轨道动力学模型，对路基不均匀沉降波长为20m的不同沉降幅值情况下的动力响应进行了研究，得出了在此情况下沉降幅值为20 mm的沉降控制标准是合理的结论.周萌等［3］通过建立三维有限元模型，通过对轨道结构在20m路基不均匀沉降波长下的受力及变形分析，肯定了文献［2］的结论，并从混凝土抗拉极限强度的角度提出了混凝土底座配受拉钢筋的建议.韩义涛等［4］通过建立车辆-板式轨道垂向动力模型，考虑路基不均匀沉降完全转化为轨面不均匀沉降，对路基不均匀沉降波长为20m的情况下的动力响应进行了计算，并引入列车速度的影响，提出了考虑车速的路基不均匀沉降限值.徐庆元等［5-6］将车体视为多刚度多自由度系统建立动力方程，钢轨及下部结构均采用大型三维有限元建立，通过轮轨力来实现两个子系统的交互计算，对列车速度为350km·h-1、路基不均匀沉降波长为20m的各种类型无砟轨道的动力响应进行了计算，并引入了温度应力的影响，提出了相关路基不均匀沉降的限值标准.

现有研究仅对特定波长情况下，路基不均匀沉降幅值影响系统动力响应进行了分析，对不同的路基不均匀沉降波长对系统动力响应的影响缺乏研究.此外，传统的车辆-板式无砟轨道动力分析方法不考虑轨道结构重力作用，在车辆荷载到达之前轨道结构会处于悬空状态（见图1a），车辆荷载到达后轨道结构开始下沉并与沉降后的路基顶面接触.这与实际情况存在明显差异（见图1b），并会带来相关动力响应的计算偏差，因而传统模型在处理这类问题时存在一定的局限性.

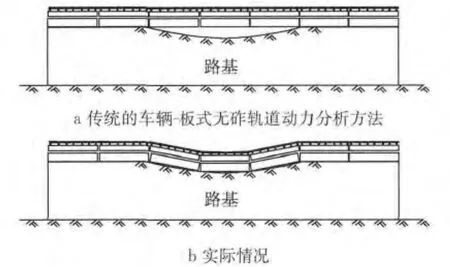
图1 列车通过前不均匀沉降情况下轨道结构示意图Fig.1 Track structure before train arrival

为解决以上问题，本文以经典车辆-轨道耦合动力学［7］为基础，推导了考虑重力的板式轨道结构振动方程，结合多刚体的车辆系统动力学模型，建立考虑重力的车辆-板式轨道垂向耦合分析模型，提出通过路基反力变化模拟路基不均匀沉降的具体方法，并对模型和方法进行了必要的验证.利用该模型和方法，针对目前板式轨道路基不均匀沉降规范限值中存在的问题，本文分析了行车速度、路基不均匀沉降幅值、波长对于车辆-板式轨道系统动力响应的影响，选择轮轨力、车体垂向加速度及轮重减载率等作为评价指标，从动力响应角度，对路基不均匀沉降规范的制定提出一定的意见和建议.

1 考虑重力的车辆-板式轨道垂向模型

1.1 车辆动力学模型

车辆被模拟为包括车体、转向架、轮对在内的多刚体系统，具有10个自由度，包括车体沉浮和点头运动、前后转向架沉浮和点头运动、4个轮对垂向运动，车体与转向架之间通过二系悬挂相连，转向架与轮对之间通过一系悬挂相连［7］.

车辆模型中各刚体在各自由度上的动力学方程可以统一表示成如下形式：

其中：M，C和K分别为车辆系统的质量、阻尼和刚度矩阵；X··，X·和X分别为车辆系统的广义加速度矢量、广义速度矢量和广义位移矢量；P为车辆系统的广义荷载矢量.车辆模型及后续提出考虑重力的板式轨道结构动力学模型的求解均采用文献［8］中新型显式积分方法进行求解.轮轨接触关系为车辆振动和板式轨道结构振动两个耦合因素之间的耦合条件，通过非线性轮轨力来模拟，轮轨力通过Hertz非线性弹性接触理论求解.

1.2 板式轨道动力学模型

在考虑重力的板式轨道结构动力学模型中，钢轨、轨道板及混凝土底座均被模拟为欧拉梁：其中钢轨的边界条件为两端简支，轨道板及混凝土底座的边界条件为两端自由.CA砂浆（水泥乳化沥青砂浆）及路基被视为离散的弹簧阻尼系统，见图2.

以y（x，t）表示欧拉梁的垂向位移，并规定其正方向为垂直向下，mr为单位长度的欧拉梁质量，EI为欧拉梁截面抗弯刚度，在欧拉梁的任意截面x处选取一微段dx，其质量为mrgdx，微段上作用有弯矩M、剪力Q及外力F（x，t）dx，见图3.

根据牛顿定律，考虑微段所受重力，忽略截面转动的影响，结合剪力、弯矩及挠度之间的关系，在垂直方向上得到考虑重力的欧拉梁振动微分方程

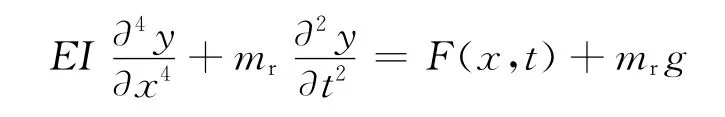
图2 轨道结构力学模型图Fig.2 Model of track structural mechanics

图3 考虑重力的钢轨微段受力分析模型Fig.3 Mechanical analysis of rail micro segment considering self-weight of structure

求解此四阶偏微分方程组采用Ritz法，结合简支欧拉梁和两端自由欧拉梁的振型函数［9］，可得到如下钢轨、轨道板和底座板的振型坐标二阶常微分方程组的基本形式：

钢轨

轨道板

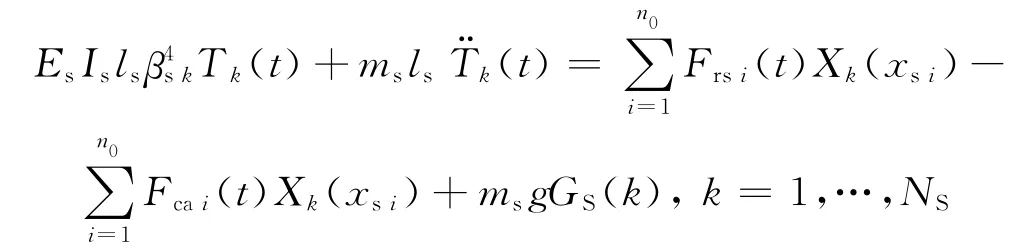
底座板

式中：ErIr，EsIs和EbIb分别为钢轨、轨道板和底座板的界面抗弯刚度；mrr，ms和mb分别为钢轨、轨道板和底座板的单位长度的质量；N，n0和m0分别为钢轨长度范围内扣结点个数、一块轨道板局部坐标系中坐标点个数和一块底座板局部坐标系中坐标点个数；xwj，xi，xsi和xbi分别为第j位车轮的运动坐标、总体坐标系中第i个扣结点位置、在一块轨道板的局部坐标系中第i个坐标点位置和在一块底座板板的局部坐标系中第i个坐标点位置；Pj（t）为第j位车轮的轮轨力；Frsi（t），Fcai（t）和Ffdi（t）分别为t时刻的扣件反力、CA砂浆支承反力和地基反力；qk（t），Tk（t）和Bk（t）分别为钢轨、轨道板和底座板的正则振型坐标；lr，ls和lb分别为钢轨长度、一块轨道板长度和一块底座板长度；Yk，Xk和Dk分别为钢轨对应的简支梁正交函数系、轨道板对应的自由梁正交函数系和底座板对应的自由梁正交函数系；βsk和βbk分别为轨道板和底座板对应的常数，其取值与ls和lb有关；NM，NS和NB分别为所截取的钢轨、轨道板和底座板振型阶数；GS（k）和GB（k）分别为轨道板和底座板对应的重力附加函数，其取值为

其中，Ck为自由梁系数.

1.3 路基不均匀沉降模拟

路基不均匀沉降在振动方程中通过以下方式体现：路基不均匀沉降直接影响地基反力，进而对整个系统产生影响，并通过非线性弹簧进行模拟.地基反力计算公式为

1.4 模型验证

为验证在车辆荷载作用下，本文提出的考虑重力的车辆-板式轨道垂向耦合模型能准确地描述系统相关动力响应，现将其与文献［5］的计算结果进行对比.假设路基不均匀沉降形式为全波长余弦不均匀沉降，其表达式为

式中：f0为路基不均匀沉降幅值；l0为路基不均匀沉降波长.

所选取用于对比的是车速为350km·h-1、轨道形式为I型板、路基不平顺波长为20m、不均匀沉降幅值为20mm工况.本文模型参数按文献［5］中取值，由于文献［5］并未对路基不平顺发生位置进行说明，本文模型计算时将路基不均匀沉降布置于两块混凝土底座（共20m长）下部.

将相关响应对比情况列于表1.

表1 动力响应对比Tab.1 Comparison of dynamic responses

由表1的对比可知，除扣件最大拉力以外其他所有动力响应与文献［5］中相比差异均在10%以内.造成两模型差值的主要原因在于轨道结构模拟形式不同带来的参数取值差异，两模型中路基不均匀沉降位置可能并不相同，德国低干扰谱随机不平顺的随机性等.但从整体而言，对比结果表明本文提出的考虑轨道结构重力的车辆-板式轨道垂向耦合系统计算结果可信，可以用来研究路基不均匀沉降对系统动力响应影响的研究.

2 路基不均匀沉降对动力响应的影响

从行车速度、路基不均匀沉降波长、波深等角度出发，对路基不均匀沉降影响系统动力响应的规律进行研究.路基不均匀沉降对列车运行的主要影响体现在安全性和舒适性两个方面.为对该影响进行量化判断，特选取轮重减载率和车体垂向加速度作为标准.

2.1 行车速度

在路基不均匀沉降波长为20m，幅值为20mm的情况下，研究车辆速度分别为100，150，200，250，300，350km·h-1时列车轮轨力、轮重减载率、车体垂向加速度的变化情况.

图4为在既有路基不均匀沉降条件下，不同行车速度下轮轨力变化图，其中灰色阴影部分为路基不均匀沉降区域.由图4可知，轮轨力在路基不均匀沉降范围内表现出先动态减小后动态增加的趋势，由于受到相邻轮对及转向架的影响，该轮对轮轨力在离开不均匀沉降区域后在一定范围内仍有波动，但波动幅度小于不均匀沉降区域.

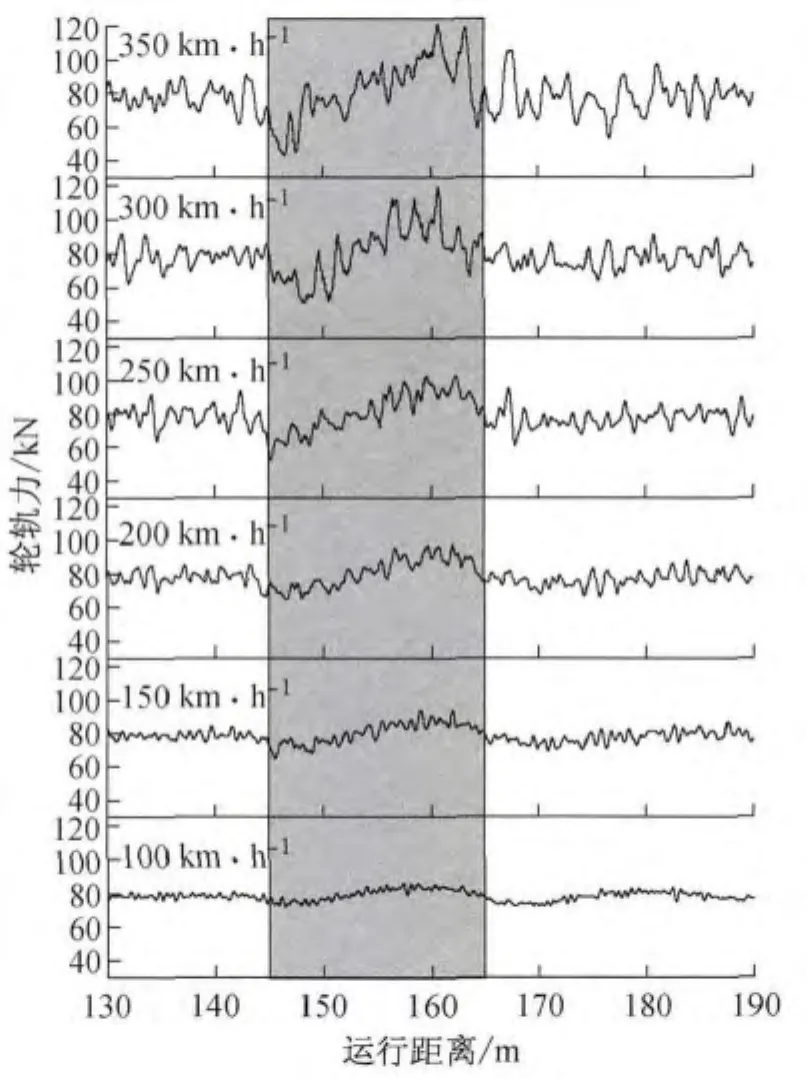
图4 不同行车速度下的轮轨力Fig.4 Wheel-rail contact forces

分别计算在不同行车速度下的轮重减载率和车体振动加速度最大值绘制于图5.由图5可知，随着行车速度的增加，轮重减载率和车体垂向加速度最大值均呈现增加的趋势.就量值而言，轮重减载率在各速度下均小于我国《高速试验列车客车强度及动力学规范》中规定的0.60的标准.而根据文献［7］中的内容，对于我国高速铁路客车，车体垂向加速度的标准为0.13g，当列车速度大于350km·h-1时，车体垂向加速度已经超过标准.

通过对不同行车速度下车辆减载率和车体垂向加速度的分析可知，随着行车速度的增加，相关动力响应均相应增加，路基不均匀沉降对车辆运行影响的控制性指标应以舒适性为主、安全性为辅.

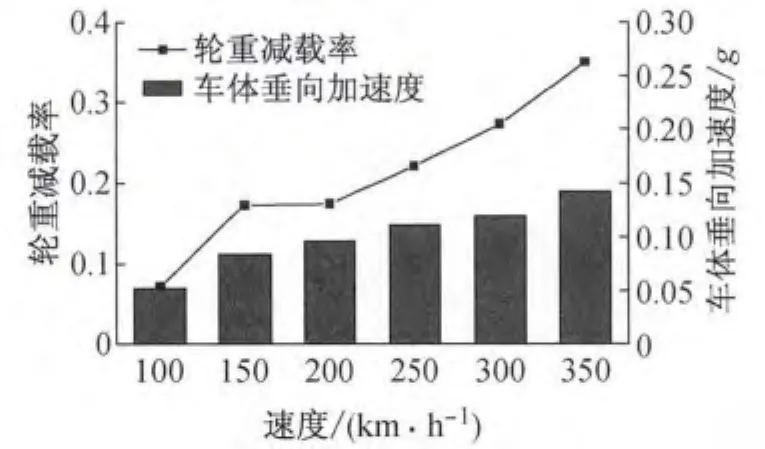
图5 不同速度下的轮重减载率和车体垂向加速度Fig.5 Maximum axle load decrement ratio and maximum vertical acceleration of vehicle

2.2 路基不均匀沉降幅值

在行车速度为100，200，300km·h-1且路基不均匀沉降波长为20m时，探究路基不均匀沉降幅值对于相关动力响应的影响，所选取路基不均匀沉降幅值分别为10，20，30和40mm.

图6为行车速度分别为100和300km·h-1时不均匀沉降幅值对列车轮轨力的影响，阴影部分为路基不均匀沉降范围.由图6可知，随着路基不均匀沉降幅值的逐渐增加，轮轨力在不均匀沉降区域的变化幅度也相应增加，速度为300km·h-1的轮轨力波动普遍大于速度为100km·h-1的情况.

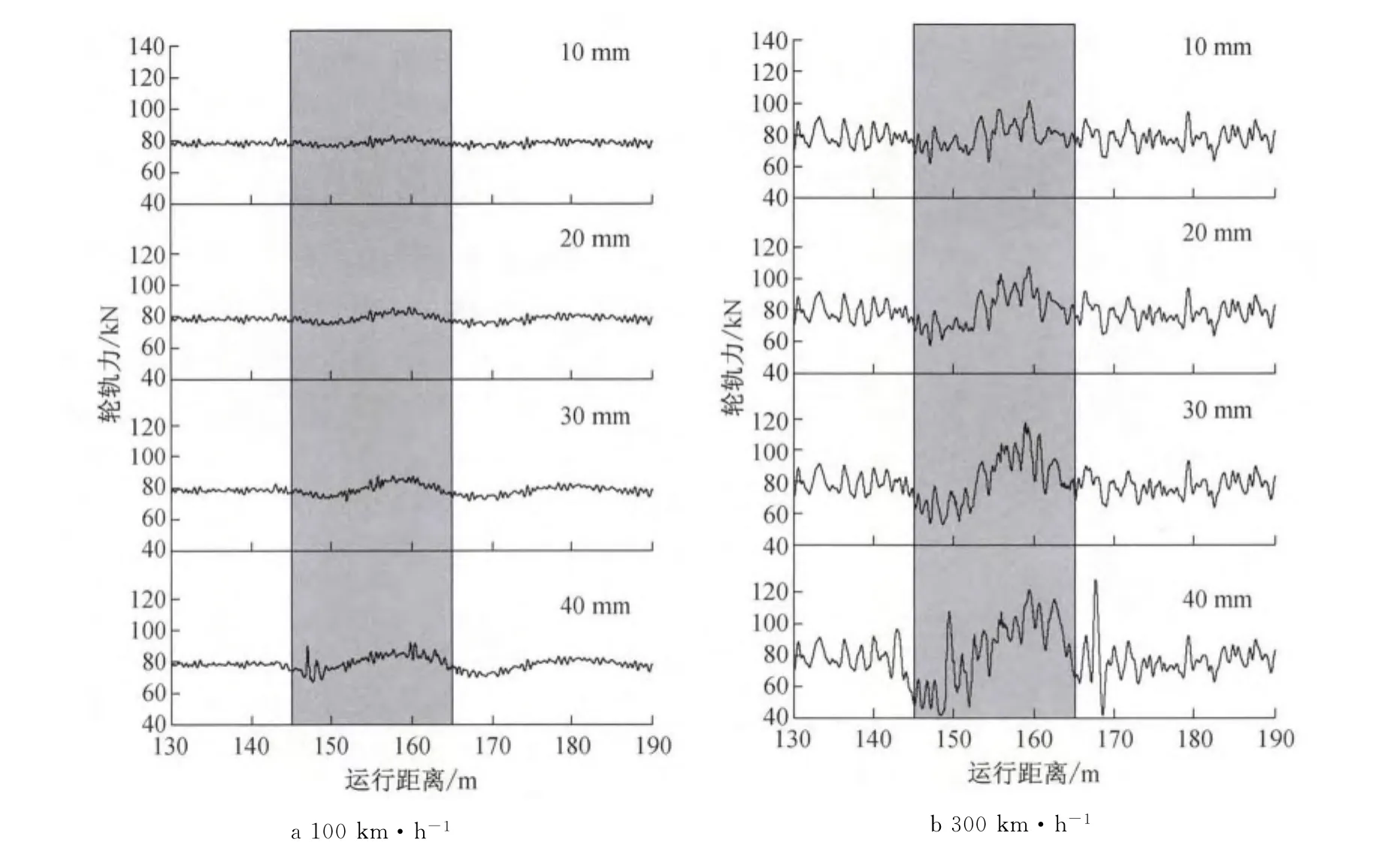
图6 不同路基不均匀沉降幅值下的轮轨力Fig.6 Wheel-rail contact forces

图7 不同路基不均匀沉降幅值下的轮重减载率Fig.7 Maximum axle load decrement ratio

通过轮轨力变化计算不同路基不均匀沉降幅值下列车的轮重减载率并绘制于图7.由图7可知，在路基不均匀沉降幅值低于30mm的情况下，轮重减载率随不均匀沉降幅值基本呈现线性变化；当幅值大于30mm时曲线斜率增加，轮重减载率变化幅度明显增大.总体而言，轮重减载率数值都低于相关规范的要求.

图8为不同路基不均匀沉降幅值下车体振动加速度变化，阴影部分为路基不均匀沉降范围.通过对车体垂向振动加速度波形的对比可知，由于模型中车辆定距为18m，与不均匀沉降波长相近，所以车体前转向架刚离开不均匀沉降范围时后转向架进入不均匀沉降范围，两转向架相继影响车体振动加速度，造成车体振动加速度首先出现两个完整的正弦波形，该正弦波长仅受到车体定距和不均匀沉降波长影响，具体表现为图8中在3种典型速度下其波长相对稳定.在两个转向架均离开不均匀沉降范围后车体在弹簧阻尼作用下逐渐恢复平稳状态，表现为继完整正弦波波形后的半波形态，该段影响距离与列车速度有直接的关系，如图8中所示，随着行车速度的增加，车体从波动影响状态恢复平稳状态所需的距离相应增加.

图8 不同路基不均匀沉降幅值下的车体垂向加速度Fig.8 Vertical acceleration of vehicle

图9为在不同行车速度下，车体垂向加速度最大值随路基不均匀沉降幅值变化的情况.由图9可知，对于行车速度为100km·h-1的情况而言，车体垂向加速度最大值在路基不均匀沉降为0～40mm时均处于0.13g限值以内；对于行车速度为200km·h-1时，也仅有幅值在40mm时超过限值；对于速度为300km·h-1，则不均匀沉降幅值为30和40 mm的车体垂向加速度超过限值.总体而言随着路基不均匀沉降幅值的增加，车体垂向加速度最大值呈现逐步增加的趋势，车辆运行的舒适性也逐步恶化.

图9 不同路基不均匀沉降幅值下的垂向加速度最大值Fig.9 Maximum vertical acceleration of vehicle

2.3 路基不均匀沉降波长

在行车速度为100和300km·h-1且路基不均匀沉降幅值为20mm时，探究路基不均匀沉降波长对于相关动力响应的影响，所选取路基不均匀沉降波长分别为5，6，7，8，10，15，20和30m.

图10为列车速度为300km·h-1时路基不均匀沉降波长对于列车轮轨力的影响，阴影部分为路基不均匀沉降范围.由图10可知，路基不均匀沉降对轮轨力的影响存在一个先增强后减弱的过程，在沉降幅值一定的情况下，相对较大和较小的波长对于轮轨力的影响均较小，而处于中间范围的波长对轮轨力的影响较大.

图11为列车速度为100和300km·h-1的情况下，轮重减载率随路基不均匀沉降波长变化图.由图11可知，当车速为100km·h-1时，其轮重减载率均小于0.6，减载率的敏感波长为10m，其他波长情况下，轮重减载率值均很小；当车速为300km·h-1时，路基不均匀波长在8～15m范围内的轮重减载率均超过了0.6的限值，减载率的敏感波长范围相比100km·h-1情况有所放大.路基不均匀沉降波长在小于8m时轮重减载率基本不随不均匀沉降波长变化，波长大于20m后减载率变化也较小.

图12为列车速度为100和300km·h-1的情况下，车体垂向加速度随路基不均匀沉降波长变化图.由图12可知，当列车速度为100km·h-1时，在0～30m的不均匀沉降波长范围内在波长为10m时达到峰值，峰值大小为0.136g；当列车速度为300km·h-1时，波长为8～20m范围时车体垂向加速度均超过0.13g的限值.

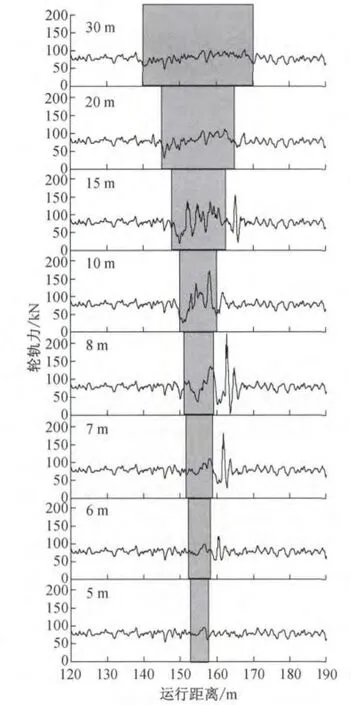
图10 不同路基不均匀沉降波长下的轮轨力Fig.10 Wheel-rail contact forces

图11 不同路基不均匀沉降波长下的减载率Fig.11 Maximum axle load decrement ratio

总体而言，车体垂向加速度随路基不均匀沉降波长变化的趋势为初始迅速增加，在波长为8～10 m时达到峰值，之后缓慢减小.考虑到模型中底座板的长度为10m，在路基不均匀沉降波长较小时，混凝土底座下脱空范围小，底座对于变形有一定的抵抗作用，轨面沉降远小于路基不均匀沉降幅值，表现出在路基不均匀沉降波长在3～6m时列车的轮重减载率和车体垂向加速度都变化较小.随着混凝土底座下脱空范围的增加，底座对于变形的抵抗能力减弱，轮重减载率及车体垂向加速度均迅速增加.在路基不均匀沉降大于10m后底座抵抗变形的能力趋于稳定，随着路基不均匀沉降的增加，轨面垂向坡度变化逐渐放缓，表现为轮重减载率和车体垂向加速度随不均匀沉降波长增加而减小的趋势.

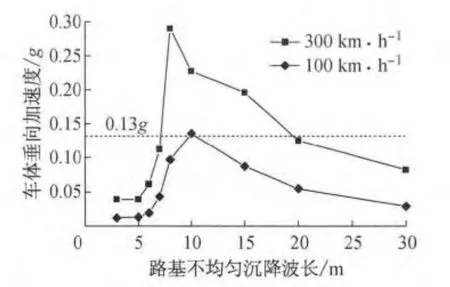
图12 不同路基不均匀沉降波长下的车体垂向加速度Fig.12 Maximum vertical acceleration of vehicle

3 结论

本文为研究路基不均匀沉降对于CRTS I型板式无砟轨道动力响应的影响，建立了考虑重力的车辆-板式轨道垂向耦合分析模型，提出通过路基反力变化模拟路基不均匀沉降的具体方法，并对模型和方法进行了验证.通过对行车速度、路基不均匀沉降幅值、波长进行研究，得到如下路基不均匀沉降影响板式无砟轨道动力响应的结论：

（1）针对在相同不均匀沉降波长和位置条件下的列车速度和不均匀沉降幅值对系统动力响应的研究表明，随着行车速度和路基不均匀沉降幅值的增加，系统动力响应均相应增加，路基不均匀沉降对车辆运行影响的控制性指标应以舒适性指标为主、安全性指标为辅，对于速度为200和300km·h-1的情况而言，波长20m下幅值大于20mm时相关动力参数超过既有标准.

（2）针对路基不均匀沉降波长对系统动力响应的研究表明，存在路基不均匀沉降的敏感波长，该波长与混凝土底座的长度有关，对于文中讨论的工况而言，8～10m为其不均匀沉降的敏感波长.在制定路基不均匀沉降标准时应考虑敏感波长，确保在最危险的波长条件下系统的动力响应仍能满足相关限值.

［1］ Hunt H E M.Settlement of railway track near bridge abutments［J］.Proceedings of the Institution of Civil Engineers-Transport，1997，123（1）：68.

［2］ 蔡成标，翟婉明，王开云.遂渝线路基上板式轨道动力性能计算及评估分析［J］.中国铁道科学，2006，27（4）：17.CAI Chengbiao，ZHAI Wanming，WANG Kaiyun.Calculation and assessment analysis of the dynamic performance for slab track on Sui-Yu Railway［J］.China Railway Science，2006，27（4）：17.

［3］ 周萌，宫全美，王炳龙，等.路基不均匀沉降值对板式轨道动力响应的影响［J］.铁道标准设计，2010（10）：1.ZHOU Meng，GONG Quanmei，WANG Binglong，etal.Effect of differential settlement of subgrade on dynamic response of ballastless track［J］.Railway Standard Design，2010（10）：1.

［4］ 韩义涛，姚力.基础沉降对土路基上板式轨道动力性能影响分析 ［J］.中国铁道科学，2006，27（4）：17.HAN Yitao，YAO Li.Analysis of the dynamic performance for slab track settlement on embankment ［J］.Journal of Railway Engineering Society，2006，27（4）：17.

［5］ 徐庆元，李斌，范浩.路基不均匀沉降对列车-路基上无砟轨道耦合系统动力特性的影响［J］.铁道科学与工程学报，2012，9（3）：13.XU Qingyuan，LI Bin，FAN Hao.Influence of uneven settlement of subgrade on dynamic characteristic of train-ballastless track on subgrade coupling system ［J］.Journal of Railway Science and Engineering，2012，9（3）：13.

［6］ 徐庆元，李斌，周智辉.CRTS-Ⅰ型板式无砟轨道线路路基不均匀沉降限值研究［J］.中国铁道科学，2012，33（2）：1.XU Qingyuan，LI Bin，ZHOU Zhihui.Study on the limited value for the uneven settlement of subgrade under CRTS-I type slab track［J］.China Railway Science，2012，33（2）：1.

［7］ 翟婉明.车辆-轨道耦合动力学［M］.3版.北京：科学出版社，2007.ZHAI Wanming.Vehicle-track coupling dynamics［M］.3rd ed.Beijing：Science Press，2007.

［8］ ZHAI Wanming.Two simple fast integration methods for largescale dynamic problems in engineering［J］.International Journal for Numerical Methods in Engineering，1996，39（24）：4199.

［9］ 曹志远.板壳振动理论［M］.北京：中国铁道出版社，1989.CAO Zhiyuan.Vibration theory of plate and shell［M］.Beijing：China Railway Publishing House，1989.