紧急避让路径跟踪自抗扰控制

赵又群，王 健，季学武，李 波

（1.南京航空航天大学 能源与动力学院，江苏 南京210016；2.清华大学 汽车安全与节能国家重点实验室，北京100084）

随着世界汽车技术和车辆控制技术的发展，车辆向着自动化、智能化方向发展.自动紧急避让系统能够利用毫米波雷达、激光雷达监测自车与前车以及障碍物之间的相对距离、速度和加速度，自动规划出避让路径，通过控制车辆前轮转角完成转向避让动作.自动紧急避让系统是一个集环境感知、规划决策、自动控制多等级和多功能于一体的综合系统［1-2］.车辆在紧急避让过程中，车速较高，存在较强的非线性和不确定性，高速车辆路径跟踪是车辆智能化发展进程中亟待解决的关键技术问题.

自动紧急避让通过自动控制前轮转向完成避让过程.国内外学者采用PID（proportion integration differentiation）控制、最优控制、鲁棒控制等方法控制车辆前轮完成自动转向过程［3-4］.虽然PID控制简单，但是对车辆特性变化鲁棒性不强；最优控制和鲁棒控制算法复杂，不利于工程应用，且算法的控制效果很大程度上依赖于被控对象模型的精度.

本文独创性地采用自抗扰方法进行车辆紧急避让路径跟踪控制研究，自抗扰控制在传统PID控制基础上进行二次开发，将现代控制理论与经典控制理论相结合，能够观测和补偿外界干扰和模型不确定性，满足鲁棒性要求［5-8］.自抗扰控制能够保证不同车型车辆很好地跟踪规划的避让路径，自抗扰控制现在已经成功应用于飞行器控制、风力发电机控制和导弹控制领域［9-12］.

1 车辆动力学模型及路径规划

1.1 车辆动力学模型

车辆二自由度动力学方程能够较为准确地反映车辆的横向动力学特性［13］.为了使设计的控制器便于工程应用，本文以二自由度车辆模型为基础，设计路径跟踪控制器.忽略转向系统的影响，直接以前轮转角作为输入；忽略悬架的作用，忽略路面不平和空气阻力影响.其中，二自由度车辆模型如图1所示.图中：lf，lr分别为车辆质心到前、后轴之间的距离；FY1，FY2分别为前、后轮所受到的侧向力；α1，α2分别为前、后轮侧偏角；u1，u2分别为车辆前、后车轮行驶速度大小；δf为前轮转角；β为车辆质心侧偏角；u为车辆质心处纵向速度；v为车辆质心处侧向速度；V为车辆质心速度.

图1 车辆二自由度模型Fig.1 Vehicle model of 2-degree-freedom

车辆二自由度动力学状态方程可以表示为

式中

其中：m为车辆质量；Iz为车辆横摆转动惯量；cf，cr分别为前、后轮侧偏刚度；γ为车辆质心横摆角速度.

对车辆二自由度车辆模型状态方程进行拉普拉斯变化，得到横摆角速度与前轮转角之间的传递函数公式为

1.2 路径规划

紧急避让过程车速较高（＞80km·h-1），规划的避让路径要求被执行机构能够执行，并且保证车辆转向过程车辆的稳定性.避让路径需要满足避障约束、侧向加速度约束、转向速度约束、曲率连续约束［14］.考虑避让路径最短，设计两段相切圆弧避让路径，并且采用三次B样条进行曲线拟合，同时保证规划的路径满足上述约束条件.以汽车质心为参考点，避让过程如图2所示.图中：R1为车辆质心转弯半径；R2为车辆右前方转弯半径；dy为质心侧向位移；dx为车辆纵向位移；Ssteer为最小避让距离；θ为车辆质心转过的角度；Hy为障碍物左侧宽度.

图2 避让过程图Fig.2 Collision avoidance

由图2可以得到如下关系式：

式中：V为车辆质心处纵向速度；μm为路面附着系数；g为重力加速度.此处限制极限工况下，仅有67%侧向加速度被利用.

当车速V=30m·s-1，μm=0.8，Hy=1.5m工况下，路径规划结果如图3所示.其中，图3a为规划的避让路径，图3b为路径曲率变化.

2 自抗扰控制器设计

对式（2）进行拉普拉斯反变换得

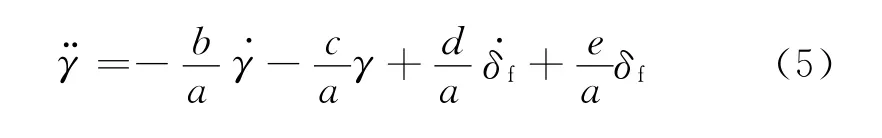
图3 路径规划图Fig.3 Path planning

令

方程（5）可以化成积分器串联型系统，即如下标准形式：

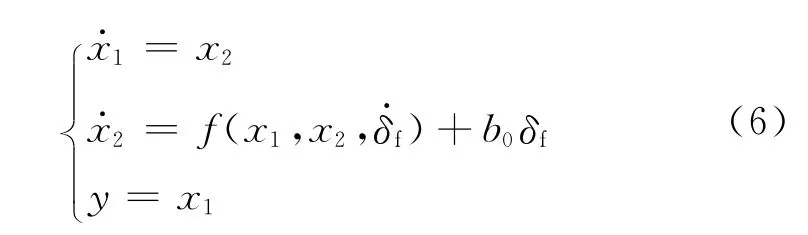
设计二阶自抗扰路径跟踪控制器如图4所示.图中：γd为理想横摆角速度；γ为实际横摆角速度；v1，v2为跟踪微分器输出；z1，z2和z3均为扩张状态观测器输出；e1，e2为非线性组合的输入误差；u0为非线性组合输出；u为被控对象实际输入；w为外界干扰；b0为设计参数.

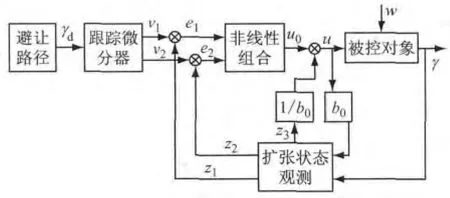
图4 二阶自抗扰控制器Fig.4 Second order active disturbance rejection controller

由图4可以看出自抗扰控制器由3部分组成：跟踪微分器、非线性组合、扩张状态观测器.其中跟踪微分器能够提取理想输入的一阶导数，并对输入信号进行滤波处理；扩张状态观测器能够将外界干扰和模型不确定性部分观测出来补偿掉.每一部分离散化表达形式如下.

（1）跟踪微分器

fhan可以表示为

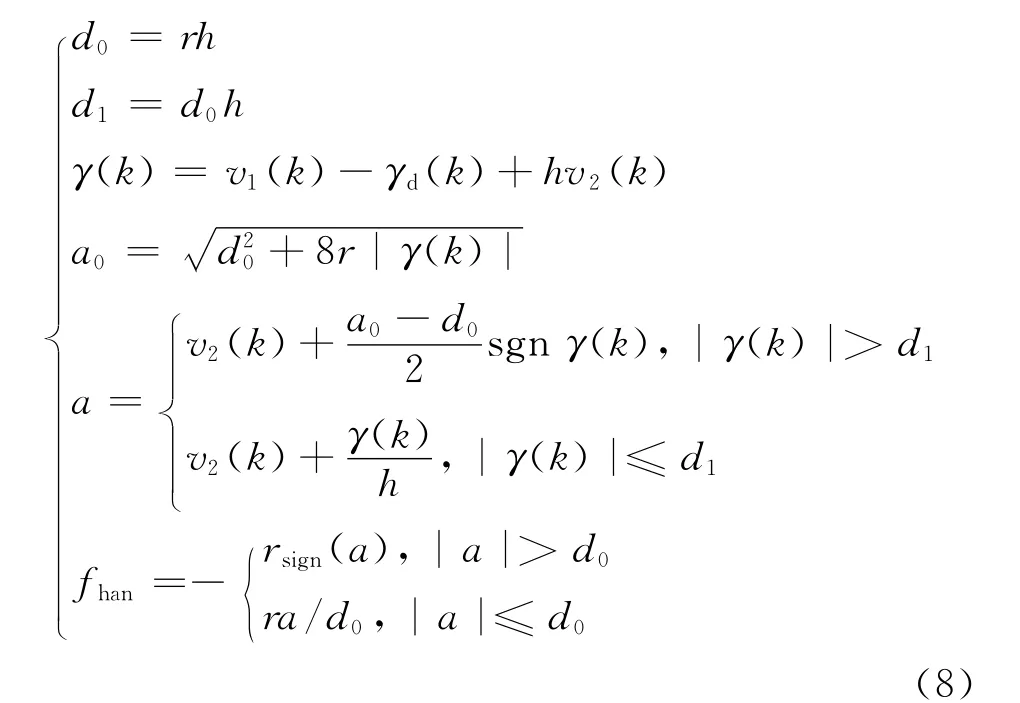
其中：γd（k）为理想横摆角速度；r和h分别为速度因子和仿真步长；v1（k）和v2（k）分别为跟踪微分器输出.

（2）扩张状态观测器

其中：z1（k），z2（k）和z3（k）均为扩张状态观测器输出.

非线性函数fal（e（k），a，δ）可以描述为

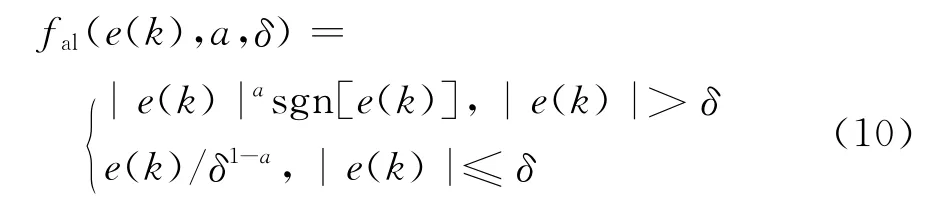
式中：a1，a2，δ和b0均为设计参数；β01，β02和β03为扩张状态观测器增益，可以表示为［15］

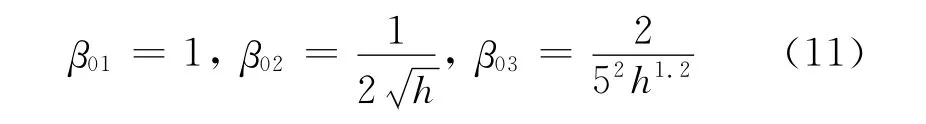
（3）非线性组合

其中：β1，β2，α01，α02和δ0均为设计参数.

3 联合仿真试验

为了验证自抗扰路径跟踪控制器的控制效果，进行软件Carsim和Simulink联合仿真验证.车辆动力学仿真软件Carsim提供了3种不同质量参数、不同轴距的车辆模型：C-Class，Hatchback；E-Class，Sedan；D-Class，Minivan.设定仿真环境：车辆纵向速度为30m·s-1，路面附着系数为0.8，Carsim输入为左右前轮转角，输出为车辆当前时刻位姿信息，路径输入为第一部分规划的理想避让路径曲线.自抗扰控制器参数经过不断调整试验得到：r=120，h=0.001，β01=600，β02=120 000，β03=8 000 000，a1=0.5，a2=0.5，δ=0.5，b0=464，β1=1.5，β2=2，α01=0.25，α02=1，δ0=0.01.不同车型跟踪理想规划路径结果如图5所示.

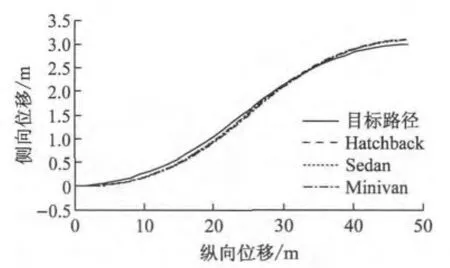
图5 路径跟踪曲线Fig.5 Path tracking

从图5可以看出，自抗扰路径跟踪控制器能够控制不同轴距、不同质量参数车辆很好地跟踪目标规划轨迹.

侧向位移误差变化曲线如图6所示.从图6可以看出，路径跟踪控制器能够控制不同车型车辆跟踪理想目标路径，且最大侧向位移偏差最大值仅为0.12m.

图6 路径跟踪侧向位移误差Fig.6 Lateral displacement error of path tracking

避让过程不同车型车辆前轮转角变化如图7所示.图8为不同车辆实际横摆角速度与理想横摆角速度变化曲线图.从图中可以看出实际路径跟踪控制器能够控制不同车型车辆快速无超调地跟踪理想横摆角速度.

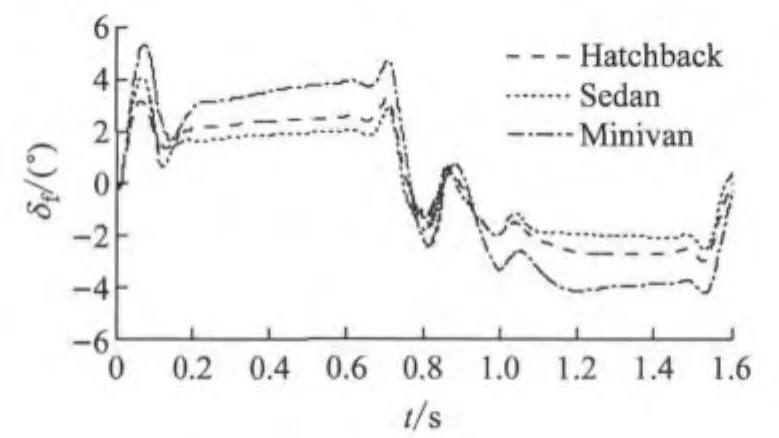
图7 不同车辆前轮转角输入Fig.7 Front wheel angle input of different vehicles

图8 横摆角速度变化Fig.8 Variation in yaw velocity

自抗扰控制器能够将外界干扰和模型不确定性观测出来，观测器观测出的干扰量变化情况如图9所示.

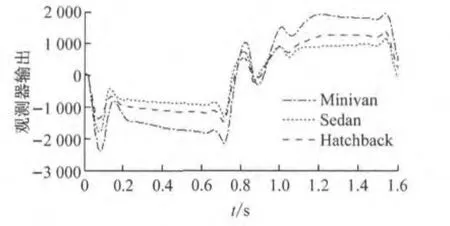
图9 扩张状态观测器输出Fig.9 Output of extended state observer

为了更加真实地显示整个避让过程，可以通过软件Carsim进行实时仿真演示，如图10所示.汽车能够安全无碰撞地避让前方车辆及其障碍物.

图10 车辆紧急避让过程演示Fig.10 Demonstration of vehicle emergency collision avoidance

4 结论

（1）联合仿真表明二阶自抗扰控制器能够保证不同轴距、不同质量参数的车辆跟踪目标路径，自抗扰控制器算法简单，便于工程应用.

（2）基于二自由度车辆模型，通过控制车辆横摆角度，设计二阶自抗扰控制器，方法简单可行.

（3）外界干扰和模型不确定性（总扰动量）可以通过扩张状态观测器观测出来加以补偿，以保证系统鲁棒性.

［1］ 徐友春，王荣本，李兵，等.世界智能车辆近况综述［J］.汽车工程，2011，23（5）：289.XU Youchun，WANG Rongben，LI Bing，etal.A summary of worldwide intelligent vehicle ［J］.Automotive Engineering，2001，23（5）：289.

［2］ 李玮，高德芝，段建民.智能车辆自由换道模型研究［J］.公路交通科技，2010，27（2）：119.LI Wei，GAO Dezhi，DUAN Jianmin.Research on lane change model for intelligent vehicles ［J］.Journal of Highway and Transportation Research and Development，2010，27（2）：119.

［3］ ZHENG Bing，Pahngroc O，Bany L.Active steering control with front wheel steering［C］∥Proceeding of the 2004 American Control Conference.Boston：IEEE，2004：1475-1480.

［4］ Tilman B，Dirk O，Bilin A G，etal.Robust vehicle steering control design based on the disturbance observer ［J］.Annual Reviews in Control，2002，26：139.

［5］ 韩京清.从PID技术到“自抗扰控制”技术 ［J］.控制工程，2002，9（3）：13.HAN Jingqing.From PID technique to active disturbances rejection control techique ［J］.Control Engineering of China，2002，9（3）：13.

［6］ GAO Qiang，SUN Zhan，YANG Guolai，etal.A novel active disturbance rejection-based control strategy for a gun control system［J］.Journal of Mechanical Science and Technology，2012，26（12）：4141.

［7］ 韩京清.扩张状态观测器参数与菲波纳奇数列［J］.控制工程，2008，15（增1）：1.HAN Jingqing.Parameters of the extended state observer and fibonacci sequence［J］.Control Engineering of China，2008，15（Suppl.1）：1.

［8］ 李一染，陈慧，高博麟.自抗扰控制在前轮主动转向控制中的应用［J］.汽车工程，2011，33（5）：388.LI Yiran，CHEN Hui，GAO Bolin.Application of active disturbance rejection control to active front steering control［J］.Automotive Engineering，2011，33（5）：388.

［9］ 陈新龙，杨涤，耿斌斌.自抗扰控制技术在某型导弹上的应用［J］.飞行力学，2006，24（1）：81.CHEN Xinlong，YANG Di，GENG Binbin.Application of autodisturbance-rejection-controller to a missile ［J］.Flight Dynamics，2006，24（1）：81.

［10］ 齐乃明，秦昌茂，宋志国.高超声速飞行器改进自抗扰串级解耦控制器设计［J］.哈尔滨工业大学学报，2011，43（11）：34.QI Naiming，QIN Changmao，SONG Zhiguo.Improved ADRC cascade decoupling controller design of hypersonic vehicle ［J］.Journal of Harbin Institute of Technology，2011，43（11）：34.

［11］ 张先勇，吴捷，杨金明.基于自抗扰解耦的变速恒频风力发电功率控制系统［J］.电气传动，2007，37（2）：8.ZHANG Xianyong，WU Jie，YANG Jinming.Power control strategy based on auto disturbance rejection decoupling for a variable speed constant frequency generation system ［J］.Electric Drive，2007，37（2）：8.

［12］ 杨苹，周少雄，胡斌，等.双馈风力发电机系统的自抗扰神经网络的励磁控制［J］.控制理论与应用，2012，29（2）：251.YANG Ping，ZHOU Shaoxiong， HU Bin，etal.Active disturbance rejection neural networks excitation control of doublefed induction generator ［J］.Control Theory &Applications，2012，29（2）：251.

［13］ 余志生，赵六奇，夏群生，等.汽车理论［M］.3版.北京：机械工业出版社，2000.YU Zhisheng，ZHAO Liuqi，XIA Qunsheng，etal.Automobile theory［M］.3rd ed.Beijing：China Machine Press，2000.

［14］ Gómez-Bravo F，Cuesta F，Ollero A，etal.Continuous curvature path generation based onβspline curves for parking manoeuvres［J］.Robotics and Autonomous Systems，2008，56：360.

［15］ 陈增强，孙明玮，杨瑞光.线性自抗扰控制器的稳定性研究［J］.自动化学报，2013，39（5）：574.CHEN Zengqiang，SUN Mingwei，YANG Ruiguang.On the stability of linear active disturbance rejection control［J］.Acta Automatica Sinica，2013，39（5）：574.