高斯Copula 的一点注记①

甘胜进，游文杰，涂开仁

(1，2.福建师范大学福清分校电子与信息工程学院 福建 福清350300;3.福建师范大学福清分校经济与管理学院，福建 福清350300)

0 引 言

p 维连续型随机变量X=(X1，X2，…，Xp)T的联合分布函数为F(x1，x2，…，xp)，边缘分布函数分别为F1(x1)，F2(x2)，…，Fp(xp)，则有:

其中诸Fi(Xi)～U［0，1］，Fi(xi)=ui，(u1，u2，…，up)∈［0，1］p.由此可见Copula 函数把联合分布函数与其边缘分布函数连接起来，是［0，1］上均匀分布随机变量的联合分布函数，能够有效研究变量间相依性，其在经济金融、风险管理等方面有着这广泛的应用.高斯Copula 函数是多元正态分布的Copula 形式，由于随机变量的单调递增变换不会改变其Copula 函数形式，故不妨设X ～Np(0，R)，其中R(＞0)为相关系数矩阵，φ(x)，φ(x)分别表示标准正态分布的分布函数和密度函数，则高斯Copula 函数为:

其Copula 密度为:

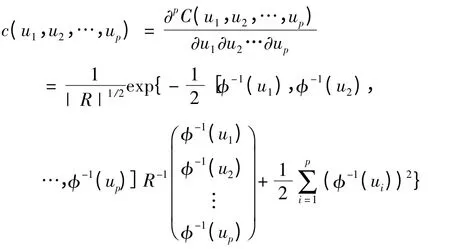
X 的联合密度函数:

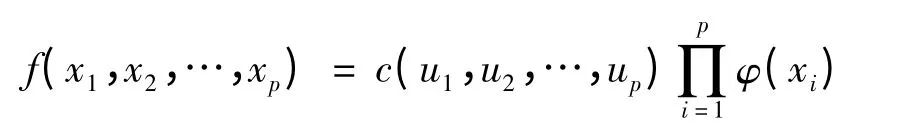
1 利用高斯Copula 函数研究二元正态变量之间的相关性

为计算方便，不妨对二元高斯Copula 进行探讨，类似的方法可以推广到多元，即

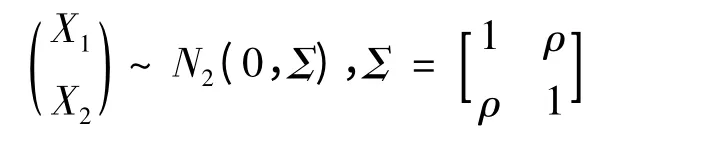
1.1 尾相依系数

称p(X2≤x|X1≤x)为度量在随机变量X1实现条件下X2实现的概率大小，当x →－∞称此时极限为极下尾相依系数(TDC)，记λL为，为了便于利用Copula 函数计算，假设X1，X2具有相同的边缘分布为F(x)，则:

性质1:λL=0.证明:

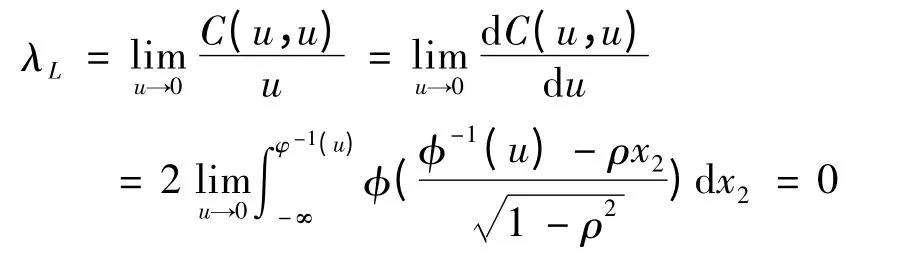
说明两正态分布在尾部是渐进独立的.

性质2: 当－1 ≤ρ1≤ρ2≤1，Cρ1(u，v)≤Cρ2(u，v)，并且C－1(u，v)=max(u+v－1，0)，C1(u，v)=min(u，v)，进而当ρ ≥0，uv ≤Cρ(u，v)≤min(u，v).

此性质的证明需要用到以下引理:

引 理［2］:(X1，X2，…，Xp)T， (X1′，X2′，…，Xp′)T分别服从Np(0，Σ)，Np(0，Σ′)多元正态分布，若Σ ≥Σ′(≥表示对应元素大小关系)，则对于任意的实数t1，t2，…，tp，有

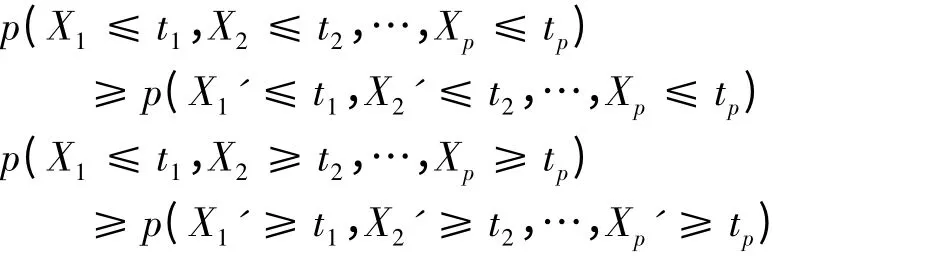
下图是使用R 软件绘出u=v 时，C(u，u)对ρ=0.5，0，－0.5 图像

1.2 尾Copula 函数.

另外一种描述尾部相依特征的是尾相依Copula 函数，下尾Copula 函数定义如下:

其中

图1 Cρ(u，u)分别对ρ=0.5，0，－0.5 图像

类似地可以定义上尾Copula 函数，在此不再赘述.当u →0 时，称)为极下尾Copula函数，而这往往是诸多学者研究的重点［3～4］.关于极尾Copula 计算，最初由文献［5］给出相关计算定理，文献［6］在此基础上稍加改动，更加一般化，定理如下:

定理1［6］:C(u，v)为［0，1］2连续函数，并且对于任意的u ＞0，v ＞0，有C(u，v)＞0，若下列极限存在:

则

其中

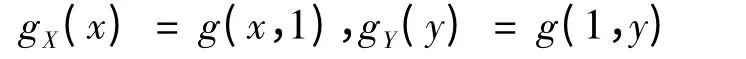
事实上，依据条件可得

故

关于高斯分布的极下尾Copula 函数计算参照文献［5］方法，可得，故y)=xy，恰好渐进独立.与下极尾相关系数得到的结论相同.

2 高斯分布的极值copula 函数.

二维高斯CopulaC(u，v)的极值Copula 函数为，为计算极值Copula 函数，作以下定义:称b(w1，w2，…，wp)=为X=(X1，X2，…，XP)T尾相依函数，显然当p =1 时，b(w1)=w1，并且b(w1，w2，…，wp)为阶数为1 的齐次函数，即b(tw1，tw2，…，twp)=tb(w1，w2，…，wp)，两边关于t 求导，然后令t=1 代入得到:

由尾相依函数定义可知:

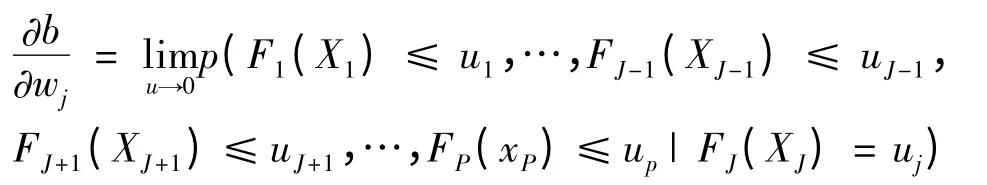
令

wI表示由wi，i ∈I 构成的集合.文献［8］证明了C(u1，u2，…，up)的极值Copula 函数:

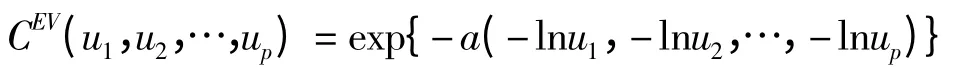
性质3: 二元正态分布的极值Copula 函数CEV(u1，u2)=u1u2

证明:

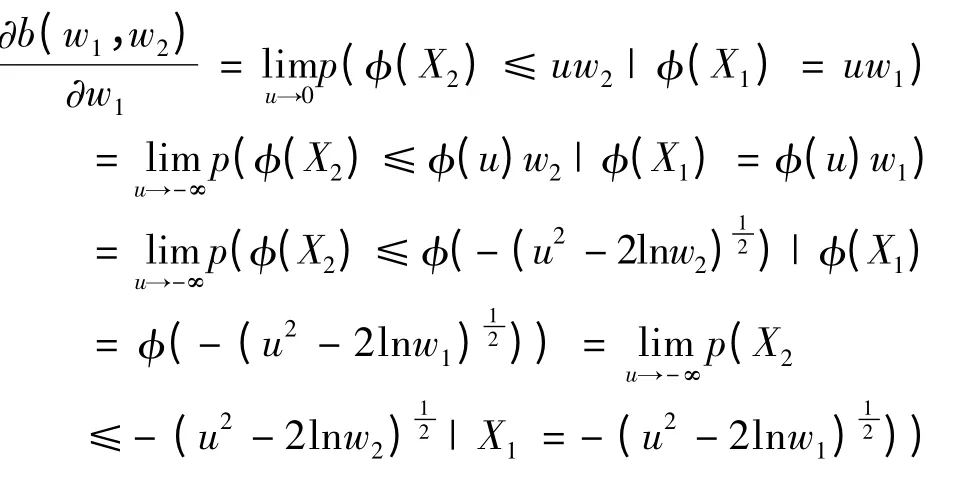
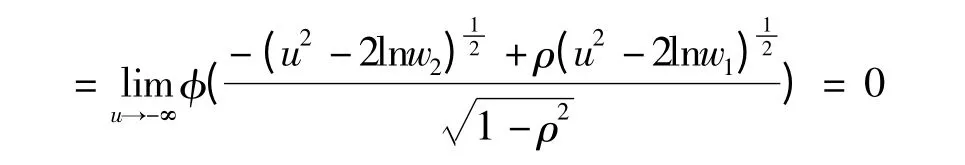
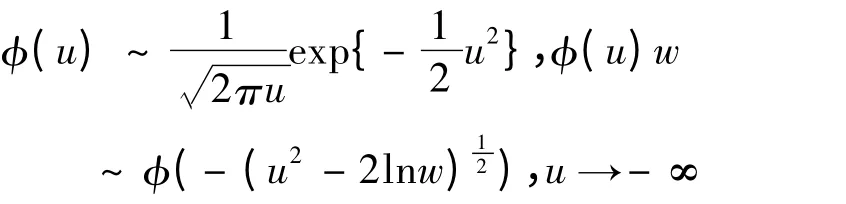
极值Copula 函数CEV(u1，u2)=u1u2，表明极值变量间也是相互独立的.

［1］ Gabriel Frahm.On the Extremal Dependence Coefficient of Multivariate［J］.Statistics＆Probability Letters，2006，76:1470–1481.

［2］ Yin Chan and Haijun Li.Tail Dependence for Multivariate T －Copulas and Its Monotonicity［J］.Insurance:Mathematics and Economics，2008，42(2):763–770.

［3］ Demarta S，McNeil A J.The t Copula and Related Copulas［J］.International statistical review，2005，73(1):111－129.

［4］ Bortot P.Tail Dependence in Bivariate Skew－Normal and Skew－t Distributions［J］.Available Online:www2.stat.unibo.it/bortot/ricerca/paper－sn－2.pdf，2010.

［5］ Alessandro Juri and Mario V.Wüthrich.Tail Dependence from a Distributional Point of View［J］.Extremes，2003，6(3):213－246.

［6］ Elena Di Bernardino and V_eronique Maume－Deschamps.Estimating Bivariate Tail:a Copula Based Approach［J］.Journal of Multivariate Analysis，2013，119:81–100.

［7］ Roger B.Nelsen.An Introduction to Copulas［M］.Second Edition.New York:Springer Science Business Media，2006.

［8］ Aristidis K.Nikoloulopoulos and Harry Joe.Extreme Value Properties of Multivariate t Copulas［J］.Extremes，2009，12(2):129－148.