嫦娥三号软着陆轨道设计与控制策略①

2015-04-14李祥宇宋艺旋袁宏俊

佳木斯大学学报（自然科学版） 2015年1期

李祥宇，宋艺旋，吕晨，袁宏俊

(安徽财经大学1.会计学院;2.统计与应用数学学院，安徽蚌埠233030)

0 引言

由于月球上没有大气，嫦娥三号无法依靠降落伞着陆，只能靠姿态调整发动机和主减速发动机，才能完成中途修正、近月制动、动力下降、悬停段等软着陆任务，本文对嫦娥三号软着陆轨道设计与控制策略进行初步研究，运用模糊C 均值聚类的方法交叉确定出粗避障和精避障的优选着陆区，并对结果进行了初步检验.同时结合动力学和运筹学的知识建立模型对燃料和时间的耗用进行计算和优化.此外还对关键指标进行敏感性分析(详见2014年全国大学生数学建模竞赛A 题［8］).

1 确定着陆器所需开普勒轨道两个关键点的参数

1.1 建模分析

首先通过研究嫦娥三号探测器软着陆的过程，了解其大致的飞行轨迹.接着根据开普勒第二定律以及机械能守恒定律求出近月点以及远月点的速度，我们假设着陆轨道与环绕轨道经度相同，最后由牛顿第二定律建立平面月球二维动力学模型，计算出近地点的纬度，最终确定近地点与远地点的位置与运行方向.

1.2 模型的建立与求解

模型一:开普勒轨道动力学模型

在此开普勒轨道上不考虑燃料消耗等重量影响因素，所以探测器的机械能守恒，结合开普勒第二定律，可以得到如下公式:

式中:v1为近月点的速度;v2为远月点的速度;r1，r2分别是开普勒轨道近月点与远月点到月球中心的距离.

由附件1 可知，月球赤道平均半径r0=1737.646km，近月点到月球中心的距离r1=15km+r0;同理，远月点到月球中心的距离r2=100km+r0，带入(1)式可求出:v1=1.7047×103m/s，v2=1.6347×103m/s.

模型二:着陆准备轨道微分方程模型［1］

为了确定近地点及远地点的具体位置，根据牛顿第二定律可知:

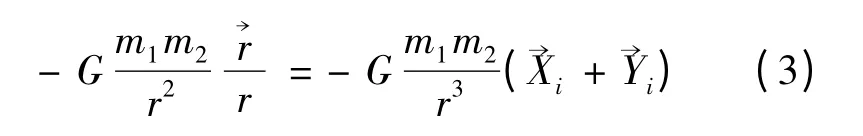
令Gm1m2=μ，化简得到探测器运动的方程组:

根据探测器运行轨道面与月球赤道平面夹角为90°的假设［3］，我们可以知道环月圆轨道与椭圆轨道在同一平面上，经度都为19.51°，以月球圆心为原点，南北极方向为轴，垂直南北极方向为轴建立着陆准备轨道与环绕轨道所在平面的极坐标系，见图1(单位:米):

图1 轨道和月球切面极坐标系

图2 月球平面直角坐标系

当近月点在A 点时，该点的纬度为θ0，而当近月点在B 点时，该点的纬度为θ0=180°－α.因此(4)式满足初值条件则该极坐标系下的近月点坐标为(1752.646，α)，远月点的坐标为(1837.646，α－180°).

2 确定软着陆六个阶段的最优控制策略

2.1 建模分析

对轨道着陆过程6 个阶段分别进行分析，以燃料消耗最少为最优控制条件对各阶段轨道进行设计控制.由于主减速段、粗避障段及精避障段三个阶段对嫦娥三号的成功着陆起着至关重要的作用，因此对着三个阶段进行主要分析;在形成大致轨道的基础上满足着落准备轨道、快速调整、缓速下降三个阶段所要求的控制条件，通过分别建立模型，采用定性和定量相结合的方法，最终得出6 个阶段的最优控制策略.

图3 粗避障优先着陆区域分析结果

2.2 模型的建立与求解

阶段一:着陆准备轨道

可将100km 轨道高度的变轨考虑为一个速度脉冲，通过齐奥尔科夫斯基公式计算飞行器的燃料消耗，即:

式中:m0为施加速度脉冲之前飞行器的质量;Δm 为产生Δv0速度脉冲所需要的燃料质量;c=veg0;ve为发动机的比冲;g0为月球引力加速度;Δv0=v1－v2.

由m0= 2400kg，Δv0== 0.07km/s，ve=2940m/s，g0=9.80665m/s2，可计算得到m =5.81988kg，又由飞行器在这一阶段消耗的燃料质量与其重质量之比小于5%，因此可忽略飞行器在这一阶段质量的缺失.

图4 精避障优先着陆区域分析结果

阶段二:主减速

模型三:平面月球二维动力学模型［2］

此时可将月球视为平面来建立月球平面直角坐标系，见上图2(单位:米):

由于嫦娥三号在距月面15km 的着陆准备轨道近月点处很小;且嫦娥三号在距月面3km 的地点处很大.因此可得在主减速阶段平均加速度水平和竖直方向的分量分别为:

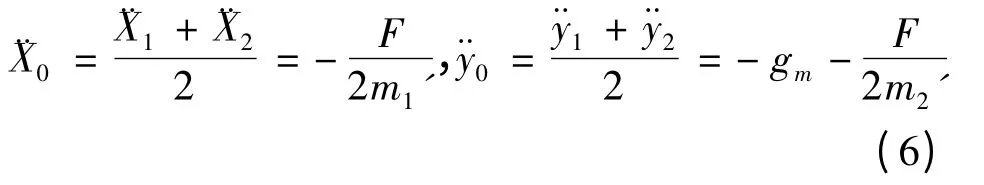
(6)式中:m1′为嫦娥三号在距月面15km 时的质量，m2′为嫦娥三号在距月面3km 时的质量，¨X1和分别表示着陆器沿水平和竖直方向的分量.

模型四:多元非线性规划模型［7］

以燃料最优为设计目标，建立此阶段燃料消耗最少的多元非线性规划模型:

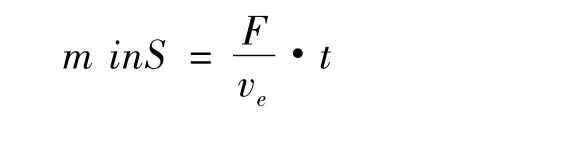
其中:根据题意和嫦娥三号实际运行轨迹，假定角γ 的余角为0°至20°的角，并且不超过20°.

阶段三:快速调整

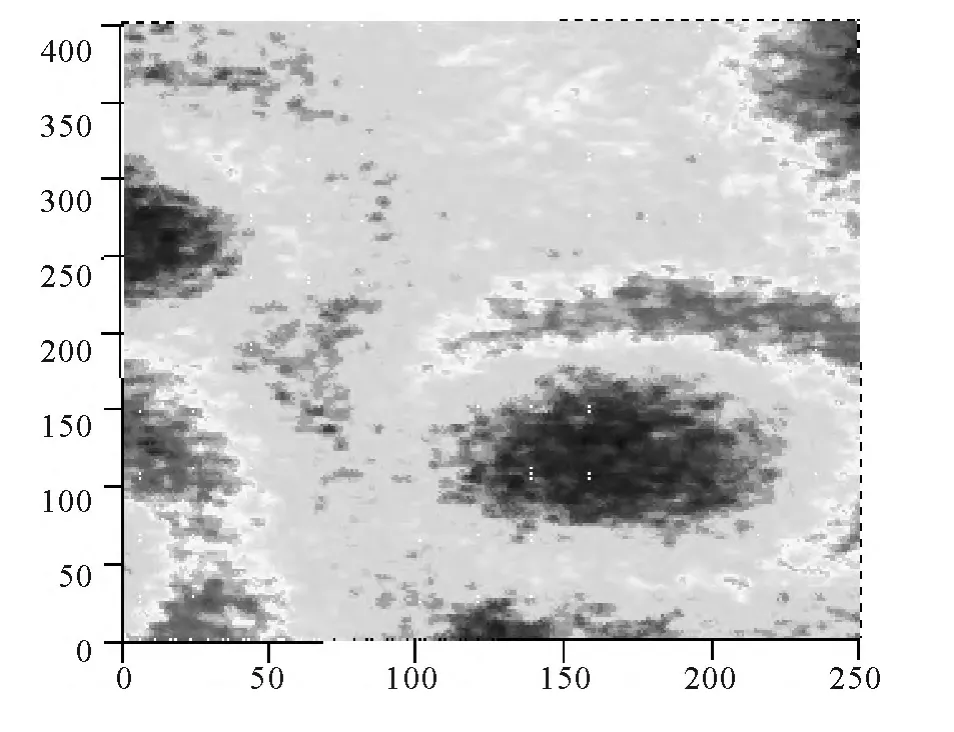
图5 粗避障优化区域

图6 精避障优化区域

在快速调整阶段中，假定探测器的推力大小是不变的，但由于其姿态在不断变化，因此发动器产生的沿着与速度方向相反的推力与水平方向的夹角在逐渐增大.且阶段所进行的时间非常短，调整的角度变化也较小，因此此阶段的燃料消耗较少，只需控制角度使其在距月面2400m 的位置水平速度变为零即可.

阶段四——粗避障和阶段五——精避障

模型五:模糊C 均值聚类模型

设X={x1，x2，…，xN}⊂Rp，Rp表示p 维实数向量空间，令uik表示第k 个样本属于第i 类的隶属度，，记vi表示第i 类的聚类中心，则X 的一个模糊C 均值聚类的就是求在上述条件下目标函数的最小值:

其中dik=‖xk－vi‖为第k 个序列到第类中心的欧几里得距离.

由拉格朗日乘数法构造新的辅助函数:

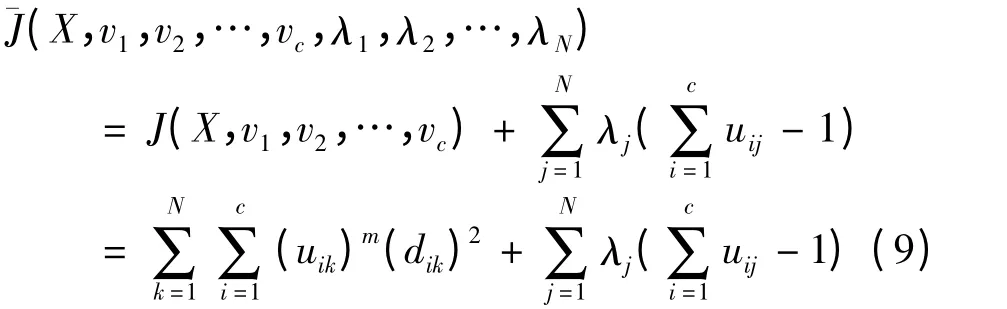
当J(X，v1，v2，…，vc)取得最小值的必要条件是(i = 1，2，…，c)，(1 ＜m)和

运用模糊C 均值聚类方法对应MATLAB 命令求解可得如下结果，见图3 和图4:

据此筛选出连续的点，大致确定粗避障优选着陆区为第801 到1200 行及第1001 到1250 列交叉部分，精避障优选着陆区行第1 到250 行与第501 到700 列交叉部分，再用MATLAB 画出相应的优化区域，见图5 和图6(单位:米):

接着对聚类结果进行标准差检验，在此条件下粗避障优选区域高度标准差c1=5.6981，精避障优选区域高度标准差的检验中，c1=7.2140，确定了安全降落的位置.

模型六:粗避障动力学模型和精避障动力学规划模型:

假定粗避障阶段着陆器做匀加速运动，则动力学模型如下:

模型②求解得:min=0.000096kg，a1=a2=1.63m/s2，t1=7.3s，t2=2.7s

说明:此两阶段是在燃料最省的情况下，做匀速运动最好，且整体纵向通过时间为10s，F推=(m0－m2－m4)gm=1708.32N.

阶段六:缓速下降

在此阶段我们可以看作飞行器以一定的速度做匀减速运动垂直下落，无水平方向速度，在距月面4m 处速度减为0.过程中速度变化较小且高度变化也较小，故反作用力做功较小，因此燃料消耗量可忽略不计.最优控制在于及时在距月面4m 处将速度减为0，为最后自由落体着陆到精确着陆点做准备.

最后把模型三、模型四和模型六合并计算得出主减速发动机推力随运行时间的最优控制策略，见图7:

图7 发动机推力随时间变化关系

图8 末段速度方向与主减速阶段燃料消耗趋势关系图

最优控制策略:在近月点瞬间开启主减速发动机使得着陆器由着陆准备轨道进入着陆轨道，并同时开启姿态发动机实时调整姿态使得主减速发动机中心始终在轨迹线上;在主减速阶段，保持主减速发动机推力7500 牛大小不变，开启501.83 秒，消耗燃料约1280.183 千克;在快速调整阶段，迅速调整姿态，使得水平速度大小为0，调整推力为1825.3 牛，开启52 秒，燃料消耗约30 千克;在粗避障阶段，调整推力为2616.66 牛，开启80.7 秒，燃料消耗约70 千克;在精避障和缓速下降阶段，调整主减速发动机推力为1708.23 牛，保持时间约为20s，燃料消耗不计.

3 敏感性分析与误差分析

3.1 敏感性分析

对主减速阶段末端着陆器速度方向与竖直方向的夹角以5 度为间隔取值，研究嫦娥三号探测器在此阶段所使用的燃料量，运用软件LINGO 求出对应不同夹角的使用燃料量，同时利用MATLAB软件做出主减速阶段所消耗的燃料随角度变化的图形，见图8:

由图8 可知，随着速度方向与竖直方向夹角的增大，在主减速阶段嫦娥三号所消耗的燃料量在逐渐减少，与之间假定较小时燃料消耗控制最优有出入，不能简单推断总体节省燃料，需要考虑各个细节.

3.2 误差分析

(1)在所确定的着陆轨道上，没有考虑着陆轨道在粗避障和精避障可能产生的水平方向上位置移动，因此会产生一定的误差.(2)在着陆轨道的6个阶段上较多考虑主减速发动机推力为大小不变方向可变的情况，没有考虑其可随时间和速度而改变的情况，对各阶段燃料消耗量的结果产生了一定的误差.(3)在建立精避障到着陆点上空4m 处的规划模型时，给出的对缓速中速度大小和运动时间的限制会产生误差.