* －素环* －Jordan 理想上广义导子的结果①

乔美玉

(吉林师范大学研究生院，吉林 长春130000)

0 引 言

一个可加映射F:R →R 被称为广义导子，如果存在一个导子d:R →R 满足F(xy)=F(x)y+xd(y)对所有x，y ∈R.设R 是一个带对合(R，*)的环，如果对aRb=aRb*=0 有a=0 或b=0，则称R 是* －素环.设R 是环，如果对所有x，y ∈R，可加映射d:R →R 满足d(xy)=d(x)y+xd(y)则称d 为导子.一个满足J*=J 的Jordan 理想J 被称为* －Jordan 理想.Ashraf 研究了满足条件的带有结合导子d 的广义导子的素环R 的交换性［1］.1981 年Bergen 研究了素环上导子和Lie 理想的关系，并得到一些结论［2］.2005 年黄述亮将Ashraf 的结论推广到了素环的Lie 理想上［3］.根据黄述亮的结果Mahmmoud EL－SOUFI 又得出一些结论.本文则是将Mahmmoud EL－SOUFI 的结论推广到*－素环上.

1 主要结果

引理1［［5］引理2］: 设R 是特征不为2 的* －素环，且J 是R 的非零* －Jordan 理想，如果aJb=a*Jb=0 则a=0 或b=0

引理2［［5］引理3］: 设R 是特征不为2 的* －素环，J 是R 的非零* －Jordan 理想，如果［J，J］=0 则J ⊆Z(R).

引理3［［5］引理4］: 设R 是特征不为2 的* －素环，J 是R 的非零* －Jordan 理想，如果d 是R 的导子，满足d(J)=0，则d=0 或J ⊆Z(R)

定理1: 设R 是特征不为2 的* －素环，J 是R 的一个非零* －Jordan 理想.设R 中有一个带有非零结合导子d 的广义导子F，且d 可与* 交换，如果满足F(u)u=ud(u)，u ∈J 则J ⊆Z(R).

证明: 由已知，

由线性变换可得F(u)v+F(v)u=ud(v)+vd(u)，对所有

在(2)中vu 换v 则有

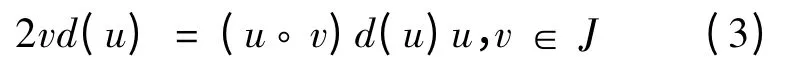
在(3)中用wv 换v 并应用(3)式可得［u，w］vd(u)= 0，对 所 有u，v，w ∈J，所 以［u，w］Jd(u)=0，由于d 与* 可交换，且J 是* －Jordan 理想

则

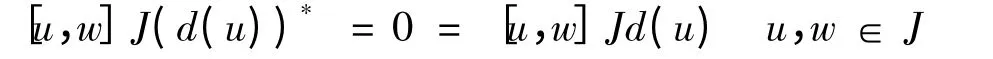
所以由引理1 有［u，w］=0 或d(u)=0，u，w ∈J

设

J1={u ∈J|d(u)=0} J2={u ∈J|［u，w］=0，对所有w ∈J}

由于J1和J2是J 的两个加法子群，并且J=J1∪J2

又由于一个群不可以写成它的两个真子群的并，则有J=J1或J=J2

若J=J1则有d(u)=0，u ∈J，由引理3 可得J ⊆Z(R)

若J=J2则有［w，u］=0，u，w ∈J，由引理2可得J ⊆Z(R)

综上所述J ⊆Z(R)

［1］ M.Ashraf，A.Ali，and R.Rani.On Generalized Derivations of Prime Rings.Southeast Asian BulletinofMathematics，vol.29，no.4，pp.669–675，2005.

［2］ J.Bergen，I.N.Herstein，and J.W.Kerr.Lie Ideals and Derivations of Prime Rings.Journal of Algebra，vol.71，no.1，pp.259–267，1981.

［3］ Huang，S.:Generalized Derivations of Prime Rings.International Journal of Mathematics and Mathematical Sciences，Article ID 85612，6 pages，Volume 2007.

［4］ Mahmmoud EL－SOUFI，Ahmed ABOUBAKR.:Generalized Derivations on Jordan Ideals in Prime Rings.Turk J Mathe 38，233–239(2014).

［5］ Oukhtite，L.:On Jordan Ideals and Derivations in Rings with Involution.Comment.Math.Univ.Carolin.51，389 –395(2010).