地下室侧向刚度对多高层框架结构的影响①

孙 洋，巢 斯

(1.同济大学土木工程学院，上海200092;2.同济大学建筑设计研究院，上海200092)

0 引 言

现在越来越多的多高层建筑结构中都带有地下室，对结构功能而言，设置地下室能使结构的基础埋置更深，同时增强其整体稳定性和抗倾覆能力.这样对于带地下室多高层结构在结构分析计算之前，必须先确定嵌固端的所在位置，若处理不恰当，可能会对结构计算带来影响.

我国结构设计规范中，对地下室顶板作为上部结构的嵌固端和相关刚度比的大小也有明确规定.《高层建筑混凝土结构技术规程》(JGJ 3－2010)［1］和《建筑抗震设计规范》(GB50011－2010)［2］中要求，当多高层建筑结构的地下室顶板作为上部结构嵌固部位时，地下一层与首层侧向刚度比不宜小于2;上海市工程建设规范《建筑抗震设计规程》(DGJ08－9－2013)［3］对这一刚度比的要求为不小于1.5.

根据规范的相关规定，当地下一层的侧向刚度与相邻上部楼层侧向刚度比大于2 时，可以选取地下室顶板作为结构嵌固端.那么刚度比的大小以及地下室顶板是否嵌固对结构性能究竟有什么样的影响值得我们思考和研究.

1 计算模型的分析与建立

工程概况:本文所选建筑是上海地区一栋10层的钢筋混凝土框架结构，地上部分九层，标准层层高3m，地下室层高6m;场地类别IV 类，特征周期为0.9s，结构抗震等级为二级，设防烈度为7 度第一组，设计基本地震加速度0.1g.简化的标准层平面图如图1 所示.

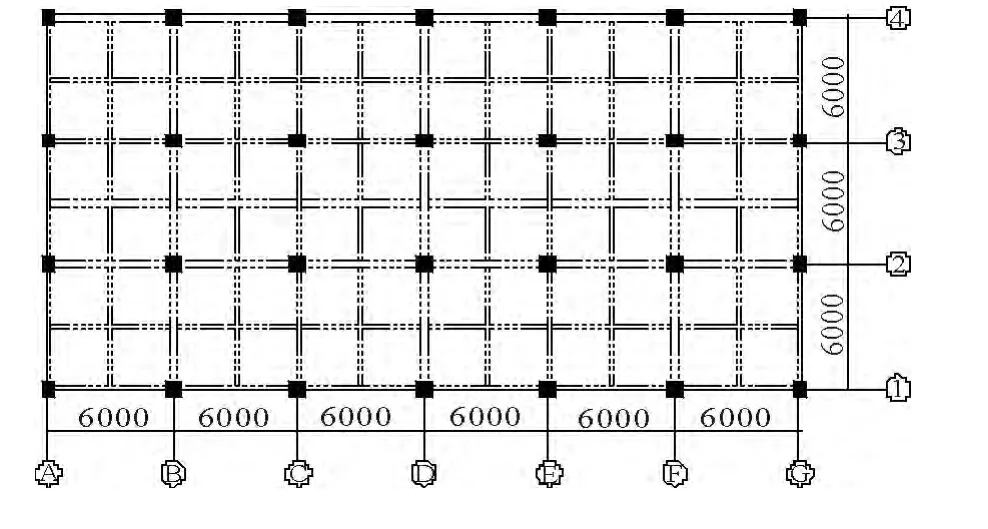
图1 标准层平面图

本文选择SATWE 软件进行分析研究.

模型的建立:柱截面为700×700，周围主梁截面为300×700，其余主梁为300×600，次梁为250×550，混凝土等级为C30;地下室顶板厚度为180mm，其余标准层板厚为120mm.

为了不改变上部结构，本文通过添加和调整地下室墙体的厚度和长度来改变地下室结构层的侧向刚度［4］，进而来对比研究地下室侧向刚度对多高层框架结构性能的影响［5］，同时考虑地下室顶板嵌固时的情况来做补充对比分析.

2 结构分析及结果

本文将取刚度比为0.5 ～5.0 等不同的几组数据，分别对结构地下室顶板嵌固和非嵌固两种计算模型进行对比分析，查看在不同情况下对结构周期、位移及内力等的影响.

2.1 刚度比对结构周期影响

本文建立了在不同刚度比情况下的分析模型，通过软件计算可以得到结构自振周期T1，如图2 所示.

为了更好研究对比自振周期随刚度比的变化规律，我们定义周期相差率u=(Ta－Tb)/Tb，其中Ta表示地下室非嵌固时结构的自振周期值，Tb表示地下室嵌固时结构的自振周期值，这样可以得到图3 的变化曲线.

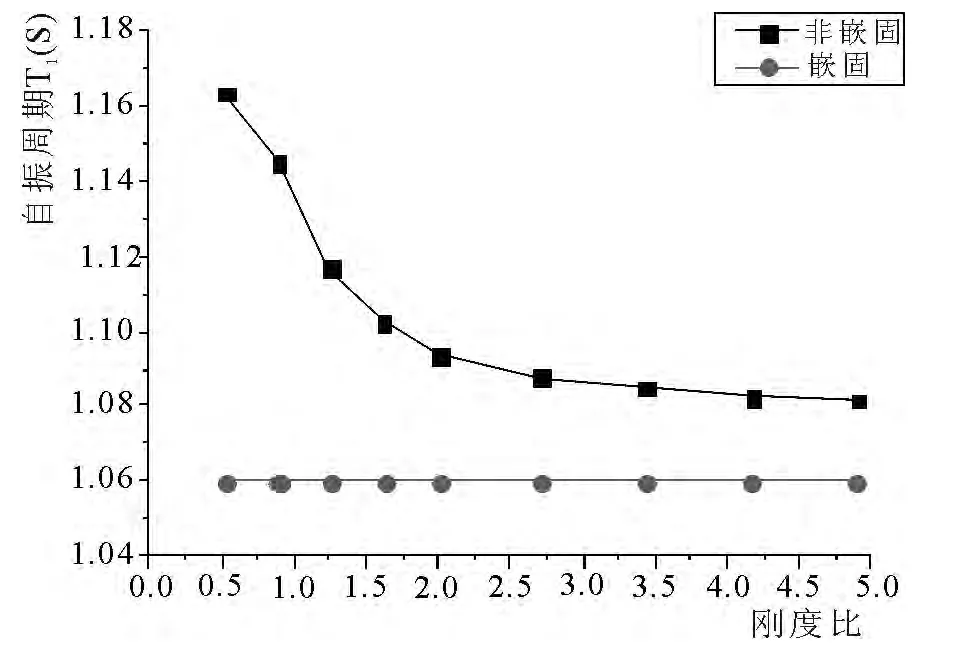
图2 不同刚度比下自振周期变化

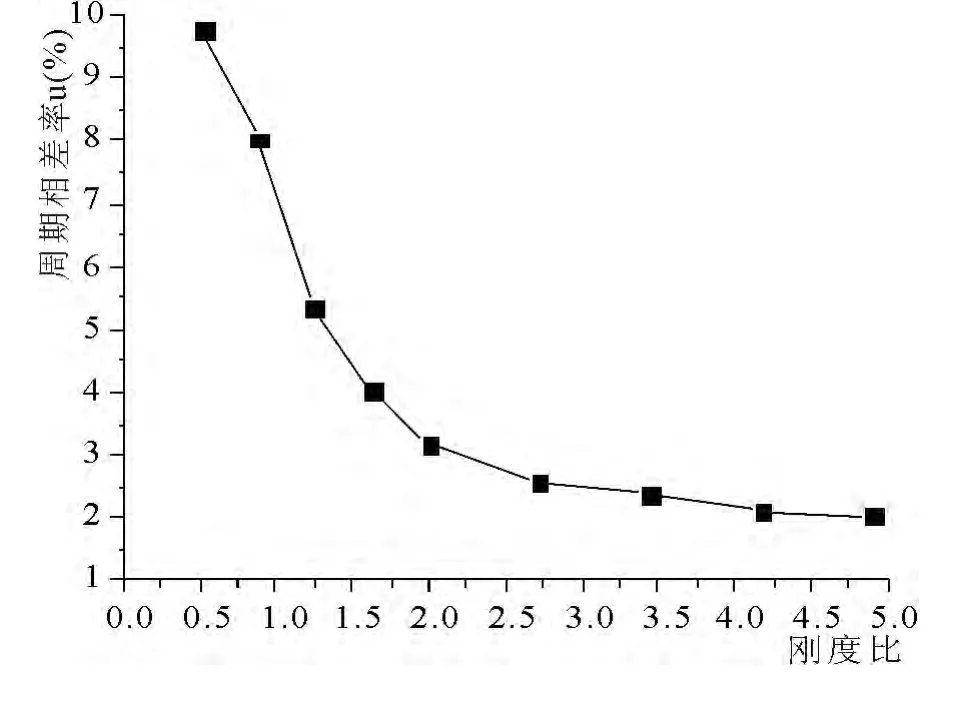
图3 不同刚度比下周期相差率变化

从图2 地下室顶板嵌固和非嵌固所得的自振周期变化趋势可以看出，随着刚度比的增加，地下室顶板非嵌固模型的自振周期不断变小，并且变化趋势越来越平缓;对于地下室嵌固模型，由于地下室刚度的变化不影响上部结构周期，故其周期变化为一水平直线.

从图3 中我们可以看到，当刚度比增加到1.5时，结构周期相差率由10%减小到5%，继续增加到2.0 时，周期相差率减小到3%左右;当大于2.0时，周期相差率变得更小，趋于一条直线.

2.2 刚度比对结构变形影响

本文通过考察结构顶点最大位移和最大层间位移角来分析刚度比变化对结构变形的影响，同时建立地下室顶板嵌固时的分析模型来予以对比.

图4 为不同刚度比下结构顶点最大位移变化情况.定义位移相差率u=(Sa－Sb)/Sb，其中Sa表示地下室非嵌固时结构的顶点位移值，Sb表示地下室嵌固时结构的顶点位移值.随着刚度比的增加，可以得到图5 的变化曲线.

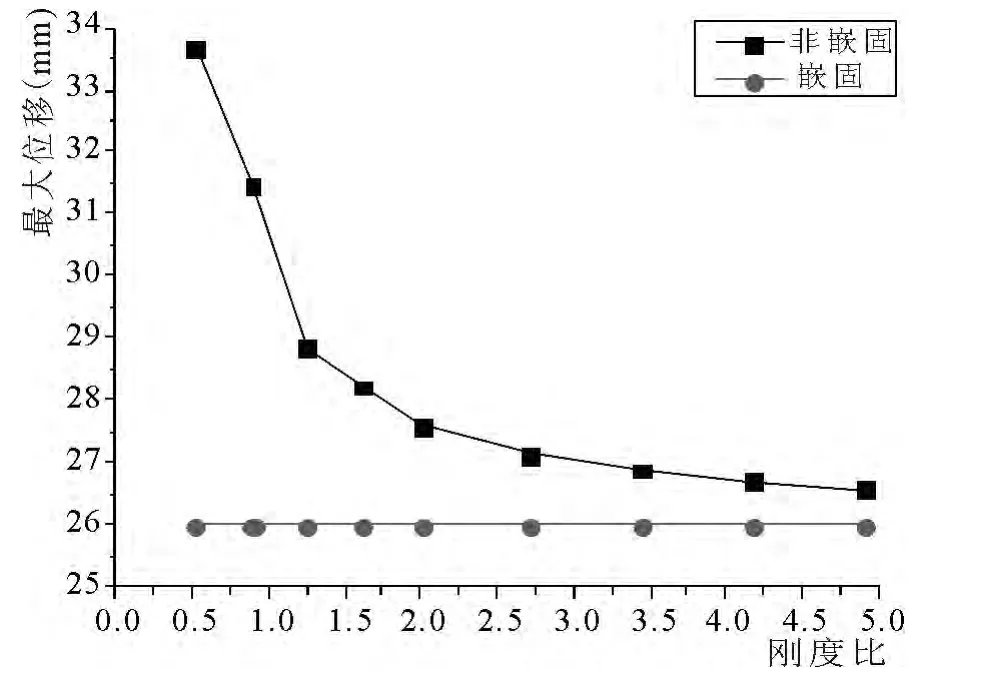
图4 不同刚度比下顶点最大位移变化

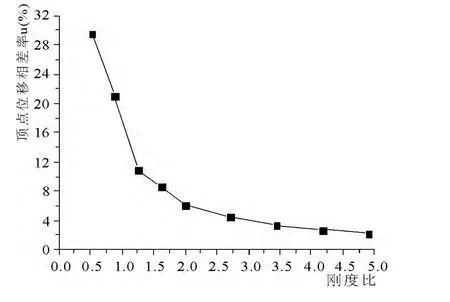
图5 不同刚度比下顶点位移相差率变化

从图4 中可以看出，对于地下室非嵌固模型，随着刚度比的增加，顶点位移从34mm 减少到27mm，当刚度比大于2.0 时，顶点位移基本不变;随着刚度比的变大，结构非嵌固的顶点位移越来越接近嵌固时的顶点位移.

从图5 中的曲线可以看出，随着刚度比的变大，位移相差率由30%减少到4%左右，当刚度比大于2.0，相差率变化很小.

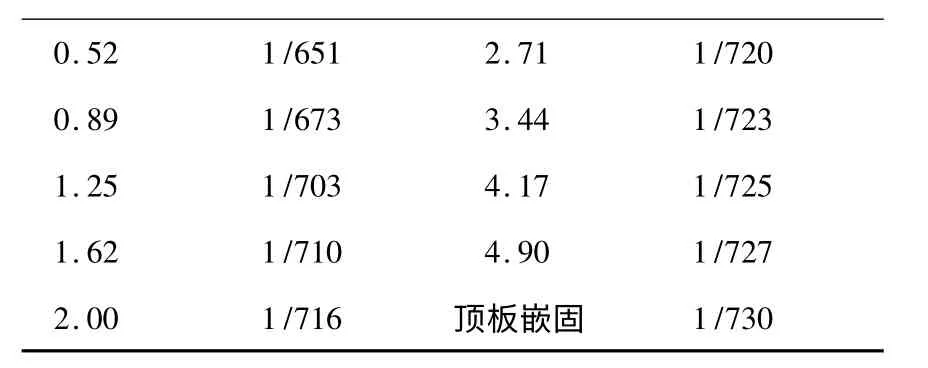
结构的最大层间位移角(均在第四层)如下表1 所示.对比在地下室顶板嵌固时结构最大层间位移角1/735，得到层间位移角相差率u 的变化曲线，如图6 所示.其中u=(θa－θb)/θb，θa表示非嵌固时结构最大层间位移角，θb表示嵌固时结构最大层间位移角.

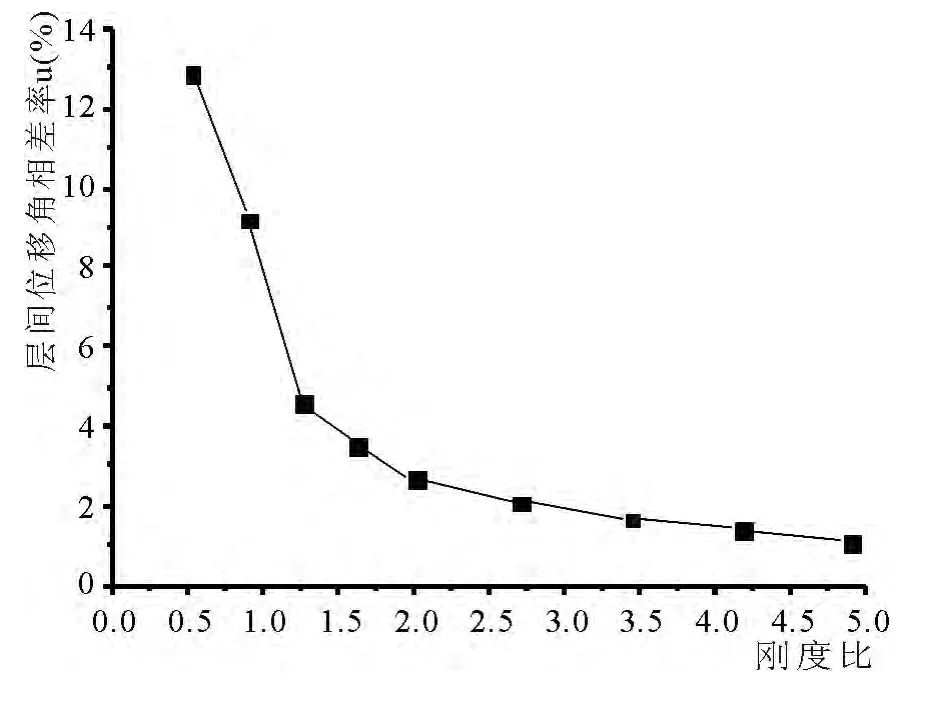
图6 不同刚度比最大层间位移角相差率变化

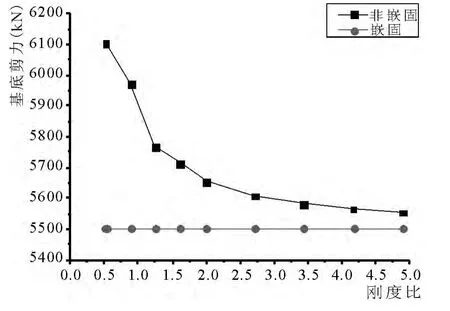
图7 不同刚度比下基底剪力变化

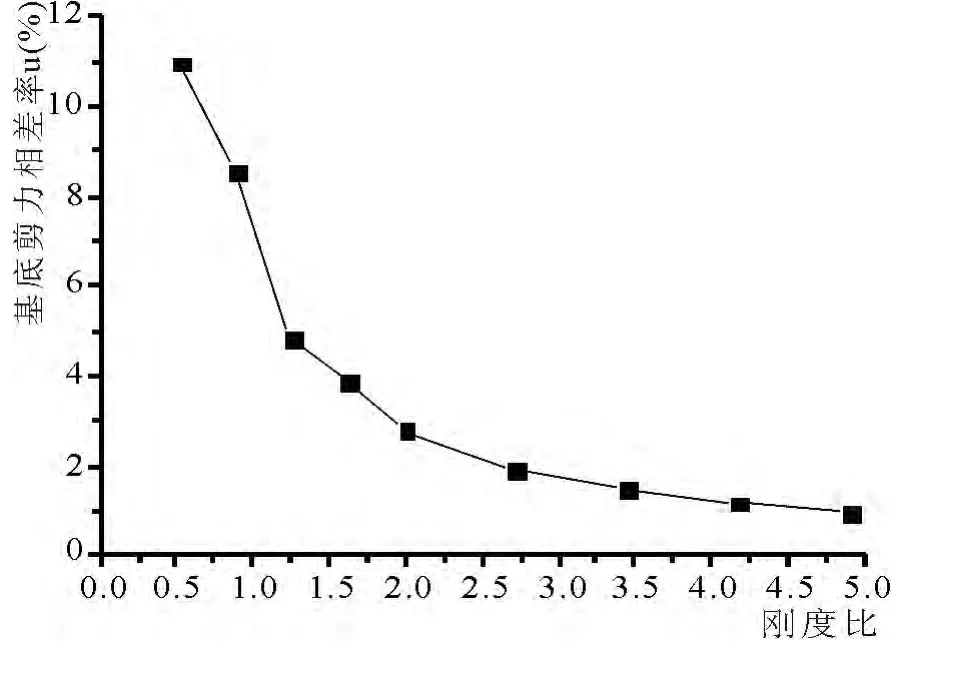
图8 不同刚度比下基底剪力相差率变化

表1 不同刚度比最大层间位移角

0.52 1/651 2.71 1/720 0.89 1/673 3.44 1/723 1.25 1/703 4.17 1/725 1.62 1/710 4.90 1/727 2.00 1/716 顶板嵌固1/730

通过分析对比表中数据和曲线变化趋势，可以得到，当刚度比不断增大时，结构的最大层间位移角在不断减小;随着刚度比的增加，结构的最大层间位移角变化越来越小，且越来越接近地下室嵌固时结构的最大层间位移角.

2.3 刚度比对结构内力影响

通过结构基底剪力和倾覆力矩的变化来说明结构刚度比的变化对结构内力的影响.定义内力相差率u=(Va－Vb)/Vb，其中Va表示地下室顶板非嵌固时结构内力值，Vb表示地下室顶板嵌固时结构内力值，我们可以得到如下图7 ～10.(注:由于要与地下室顶板板嵌固时做对比，基底剪力和底层倾覆力矩取地上一层底部的数值.)

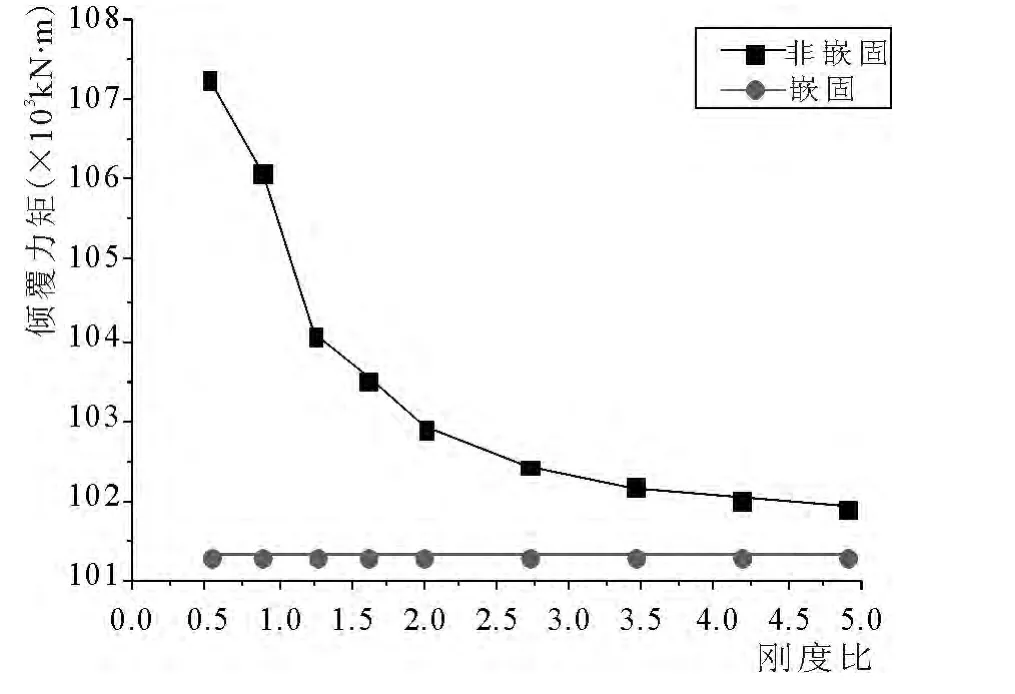
图9 不同刚度比下结构倾覆力矩变化

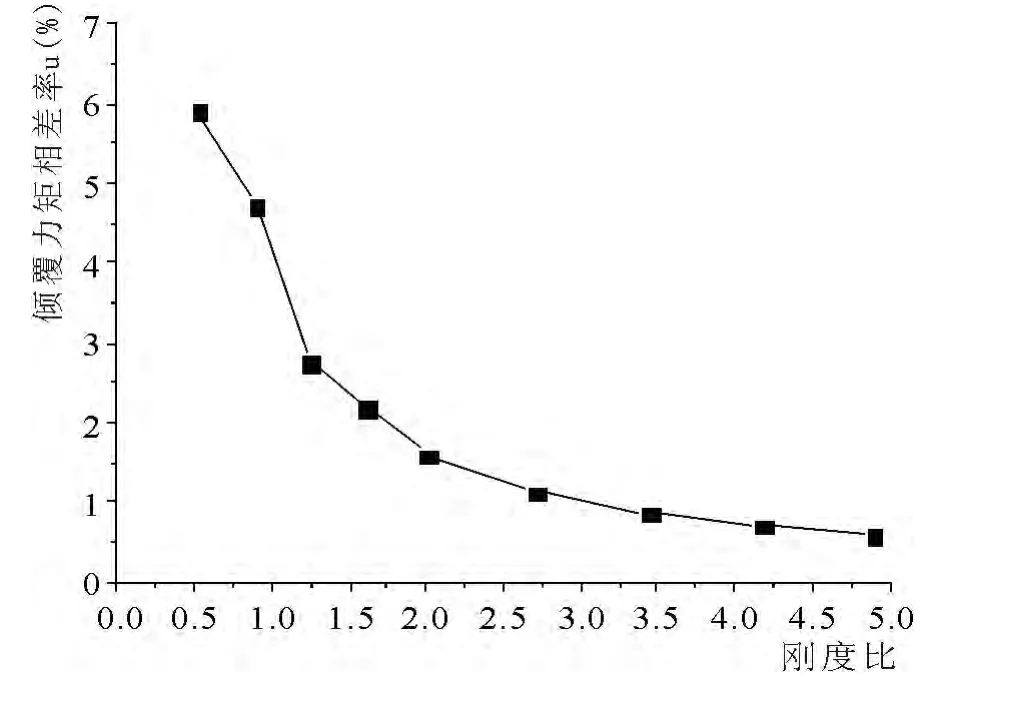
图10 不同刚度比下倾覆力矩相差率变化

从图中曲线的变化情况，可知结构底层倾覆力矩的变化情况同基底剪力变化情况非常相似，当刚度比在0.5 ～2.0 变化时，结构的基底剪力和底层倾覆力矩都慢慢变小，并且变化率越来越小，当刚度比大于2.0 时，曲线变得非常平缓;当刚度比在0.5 ～2.0 变化时，结构内力的相差率由6%减小到1%，当刚度比大于2.0 时，相差率趋于0，结构基底剪力和倾覆力矩接近地下室顶板嵌固时的情况.

根据理论分析［2］，随着地下室侧向刚度的增加，结构自振周期会减小，相应于结构基本自振周期的水平地震影响系数会增加，这样地下室基底剪力会增大，但由于地下室与上层结构的刚度比越来越大，这样就可能会导致地上一层的基底剪力越来越小，这也是图7 中显示的结果.

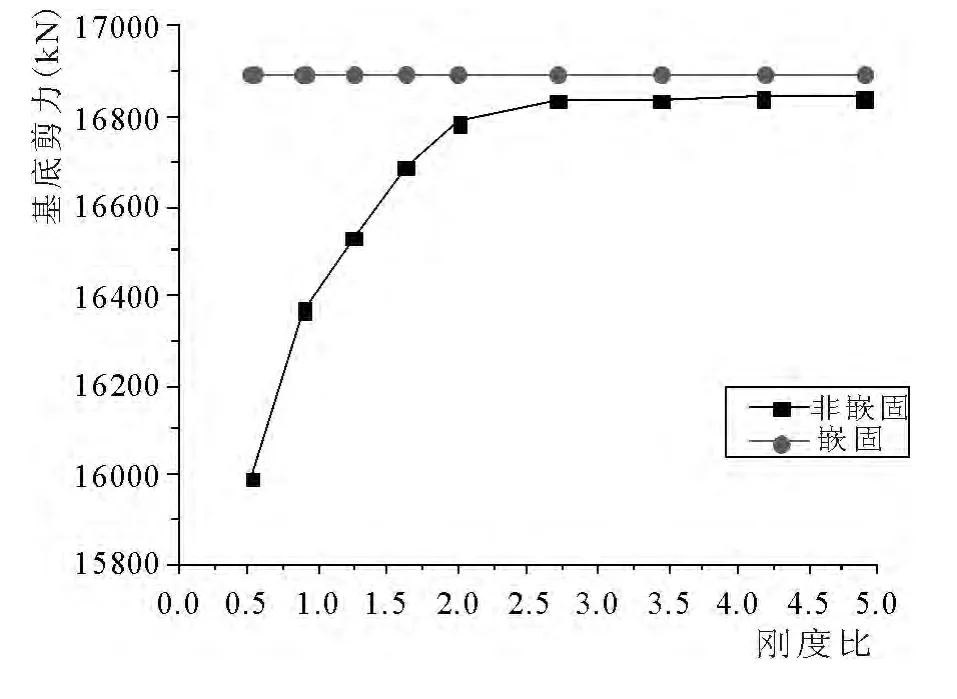
图11 大震下不同刚度比时基底剪力变化

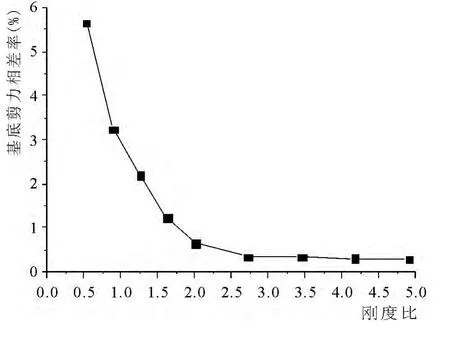
图12 大震下不同刚度比时基底剪力相差率变化

2.4 在大震作用下刚度比对结构影响

为了分析在大震下刚度比的变化对结构性能的影响，本文利用EPDA 软件对结构进行Pushover分析，同时与地下室顶板嵌固时的分析结果进行对比，分析得到结果如下:

(1)随着刚度比不断变化，在相应大震下性能点处的最大弹塑性层间位移角如下表所示:

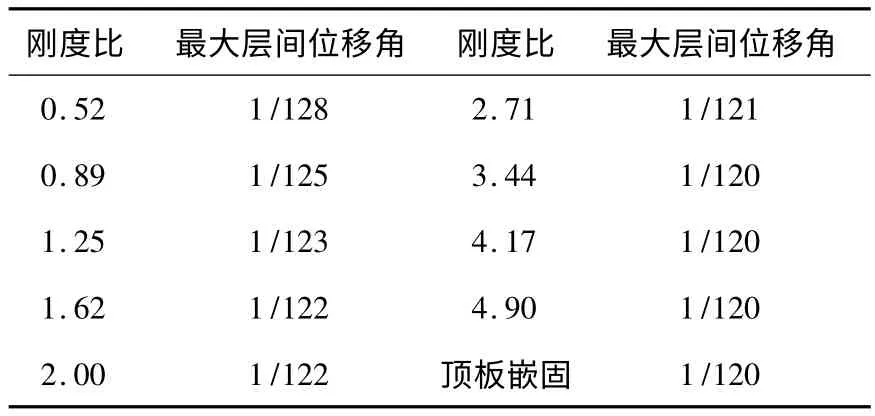
表2 大震下不同刚度比的最大弹塑性层间位移角

从上表可以看到，随着刚度比的增加，结构在大震性能点处的最大层间位移角都小于1/50，满足规范要求，且变化都很小，与地下室顶板作为嵌固的假定条件基本无影响.

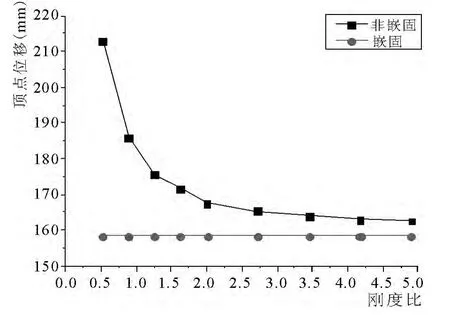
图13 大震下不同刚度比时顶点位移变化

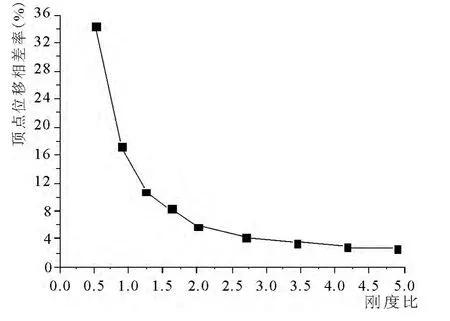
图14 大震下不同刚度比时顶点位移相差率变化

(2)随着刚度比的变化，结构在大震性能点处的基底剪力及其相差率变化如下图11，12 所示:

从上图中可以看出，随着刚度比的增加，结构在大震性能点处的基底剪力在不断增加;当结构刚度比大于2.0 时，基底剪力变化趋于平缓，且接近顶板嵌固时结构的基底剪力.

(3)随着刚度比的变化，结构在大震性能点处对应顶点位移及其相差率的变化如下图13，14 所示:

从上图可以得到，当刚度比从0.5 增大到2.0时，结构在大震性能点处对应顶点位移从215mm减小到165mm;当刚度比大于2.0 时，顶点位移基本保持不变，相差率也减小到2%左右，说明此时结构的顶点位移接近地下室顶板嵌固时的顶点位移.

3 结 论

通过以上的分析和研究，我们可以明确地下室侧向刚度的变化会对多高层框架结构的性能产生影响，正确选取嵌固端及计算模型对结果有密切联系.经过计算分析，可以得到以下结论:

(1)对于带地下室的多高层框架结构，随着刚度比的不断增加，结构的自振周期、顶点位移、层间位移角、基底剪力(地上一层)和倾覆力矩都在不断减小，且变化率越来越小［7］.

(2)分析对比框架结构地下室顶板嵌固与非嵌固时的结果，可以得到当刚度比不断变大时，结构的自振周期、位移及内力的相差率都不断减小，并且当刚度比超过2.0 时，相差率变得很小(小于4%)，在实际工程许可的范围内，这说明此时地下室顶板能满足实际嵌固的相关要求，可以作为嵌固端，与规范相符.

(3)随着刚度比的变化，结构在相应大震性能点处所对应的最大弹塑性层间位移角影响很小，且都慢慢接近地下室顶板嵌固时的情况.

(4)在大震作用下，结构在性能点处的基底剪力随着刚度比的增加而不断增加，在性能点处对应顶点位移随着刚度比的增加而不断减小;当结构刚度比大于2.0 时，基底剪力和顶点位移变化趋于平缓，且接近地下室顶板嵌固时的情况.说明在大震作用下，当刚度比大于2 时，是否对结构地下室顶板进行嵌固对结构性能影响不明显.

［1］ 高层建筑混凝土结构技术规程(JGJ 3—2010)［S］.北京:中国建筑工业出版社，2011.

［2］ 建筑抗震设计规范(GB50011—2010)［S］.北京:中国建筑工业出版社，2011.

［3］ 建筑抗震设计规程(DGJ08－9－2013)［S］.上海.

［4］ 陈春梅.地下室嵌固作用对不规则结构下的侧向刚度的影响［J］.工业建筑，2014，04:167－170+166.

［5］ 程志辉，张俊胜.带地下室高层结构的动力计算模型［J］.华南理工大学学报(自然科学版)，2005，06:89－93.

［6］ 钱光亮.高层建筑嵌固端合理选取的判定条件与研究分析［D］.合肥:合肥工业大学，2012.

［7］ 张朝云.带地下室高层建筑结构嵌固端的选择及相关问题研究［D］.重庆:重庆大学，2008.