无人机光电侦察平台的动目标测速方法研究①
2015-04-14周春祎黄大庆
周春祎,韩 伟,黄大庆
(1.南京航空航天大学电子信息工程学院,江苏 南京210016;2.南京航空航天大学无人机研究院,江苏 南京210016)
0 引 言
近年来,无人机的迅速发展促进了其相关领域的科学研究.在无人机的军事侦察过程中,运动目标的即时速度是很重要的一项侦测数据,已经引起了学术界的高度重视.对运动目标的打击能力主要体现在打击的快速性以及准确性,需要武器系统在较短的时间内实现瞄准、定位和测速,对目标的快速发现和跟踪测量以及飞行器的高精度定位是实现对运动目标实时测速的基础和前提.在现代战争中,无人侦察机具有独特的优越性和灵活性,常负担战场侦察和目标监视的重要任务[1].多年来,无人机研究机构主要致力于基于光电侦查平台针对目标的定位的研究并取得一定的成果,但对无人机基于光电侦查平台针对运动目标测速的研究则相对滞后,不能完全满足作战需求.
以往的运动目标测速方法大都是借助基于多普勒效应的雷达测速.相比雷达测速,基于光电侦察平台的测速具有简单易行,方便灵活,可接应用于无人机的地面侦查任务.而本文就是利用无人机机载光电侦察平台来实现对运动目标的速度测量.此外,对于影响无人机测速精度的各种误差影响因素进行了初步的研究和分析.通过机载侦察设备,通常可以得到目标相对载机的距离、方位角和俯仰角等信息[2].在此基础上建立计算测量模型,极大降低了运算的复杂程度.
1 测速系统构成
本文探讨的动目标测速方法是以目前无人装备的光电侦察平台、惯性导航系统等设备为基础的.惯性导航系统是一种自主式导航系统,利用惯性仪表测量载机在惯性空间中的角运动和线运动,精确计算运动载体的位置、速度和姿态角等载机的运动信息.
光电侦察平台目前主要采用吊舱式或转塔式结构倒挂安装在无人机上.它能够利用其稳定的跟踪功能,保证获取清晰的图像,不受载机位置和姿态变化以及其他干扰力矩所造成的光轴在惯性空间内的抖动[4],并保持目标目标图像始终位于摄像机视场中心,实现对目标的稳定跟踪,并提供目标测速时光电侦查平台的光轴指向角.同时,系统配置的激光测距仪可以测量无人机与被测目标的即时距离.
由此可知,当对运动目标测速时,光电侦察平台摄像角、无人机与目标的距离以及无人机的位置和姿态信息均可通过测量获取.
2 运动目标测速的数学模型
2.1 动目标测速原理
动目标测速的主要工作原理是在光电侦察平台能够对运动目标实时跟踪的基础上,根据稳定平台/激光测距模型提供的俯仰角、方位角和距离测量目标的距离[5],并结合无人机的三维姿态,经过转换计算,应用到本文所建的数学模型中,实现对运动目标的测速.
在相邻采样过程中,T1时刻与T2时刻间可认为无人机是保持相对地面高度不变的匀速直线飞行,所检测的运动目标为匀速直线运动.测得T1时刻到T2时刻间运动目标的运动距离ΔS,再除以采样时间间隔ΔT,就可以获得此运动目标的瞬时速度标量同理,速度的方向可结合运动目标的方向和载机的航向进一步获得.
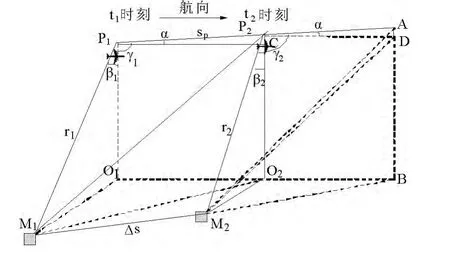
图1 动目标测速原理图
2.2 建立数学模型
如图1 所示,在采样时段内设定无人机由P1点向A 点方向飞行,分别在采样t1,t2时刻于P1,P2点对运动目标进行观测.同时,在t1时刻,运动目标位置在M1点;在t2时刻,目标运动到M2点.O1,O2点分别为P1,P2点对地面的垂直投影.
在本数学模型中,令采样时间间隔为ΔT,间隔内目标运动距离即M1点到M2点的距离为Δs;令P1点到M1点的距离为r1,P2点到M2点的距离为r2,均由激光测距仪测得;令P1点到P2点间的距离为sP,可由载机即时速度和时间Δt 获得;令图中∠AP1C=∠AP2D=α,可由GPS/INS 系统可获得无人机在T1和T2时刻的大地直角坐标,并在大地直角坐标系中结合向量得 知α;令图中,均可由光电侦察平台摄像角(包括摄像方位角、摄像高度角)结合惯导给出的载机姿态角(包括载机的俯仰角,偏航角和横滚角),结合坐标系间的转换(包括基座坐标系,载机坐标系,载机地理坐标系和大地直角坐标系),可以得到∠β1,∠β2,∠γ1和∠γ2.
首先,由图1 中的数学关系可以求出以下变量:

由(2)式可计算求出:
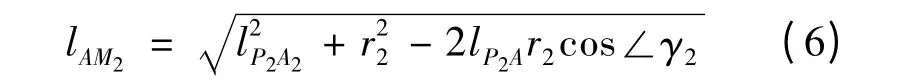
(6)由(1)、(3)式可计算求出:

根据反余弦定理,结合(7)可求出:

由(4)、(5)可求出
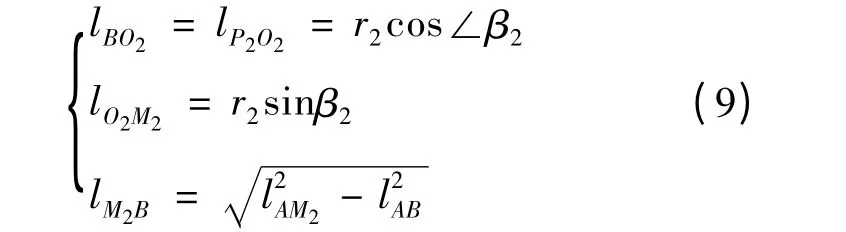
根据反余弦定理,结合(9)可得到:

最后,由(5),(7),(8),(9),(10)的结果可计算得出:

由以上公式推导可获得运动目标在抽样间隔内的距离S,进而获得运动目标的瞬时速度标量v.速度的方向可结合运动目标的方向和载机的航向进一步获得,即取得的夹角θ 即可.综上所述,可以有此数学模型进行无人机实现对运动目标测速的初步探索.
3 测速误差分析
由推导出的数学模型可知,测得的运动目标速度都是激光测距仪测出的载机与运动目标距离r1,r2,采样时间内载机的飞行距离sP,以及惯导测出的载机姿态角结合光电侦察平台摄像、测距角度所决定的α,β1,β2,γ1,γ2这几个变量组成的函数.由此可以得知本测速模型的误差分量有:1、激光测距仪的测距误差δr;2、惯性导航系统引入的载机速度的误差δsp;3、飞机姿态角及平台摄像角度共同引入的系统测量角度的误差δα,δβ,δγ.
3.1 误差来源
(1)激光测距仪引入的误差δr
在测速过程中,载机与运动目标的距离由光电侦察平台中的激光测距仪直接测量获得.激光测距仪是利用发射的激光信号经目标表面反射后被接收系统接收,实现对目标的距离测量及成像跟踪的主动式传感器系统.其分辨率高、抗干扰能力强,不仅可以精确测距,能协助实现对目标的精确测速和精确跟踪.
激光测距机在其他变量(大气和目标特征变量)确定的条件下,对目标测距误差的大小主要取决于系统内部脉冲形成电路所选用的晶振频率f1的高低,闸门电路计数误差为±1E 个脉冲.整个有效测量范围内的任何位置的测距误差的绝对值为(C 为光速).
(2)飞机的速度引入的误差δsp
本数学模型中单个采样时间内飞机的飞行速度直接由惯性导航系统给出的载机即时速度获得,即sp=vp·Δt.因此,飞机的速度引入的误差δsp=δv·Δt.
(3)系统测量角度的误差δα,δβ,δγ
本数学模型中,α,β1,β2,γ1,γ2这几个角度都是通过惯性导航系统载机姿态角(横滚角φ1、俯仰角φ2、偏航角φ3)结合光电侦察平台摄像角(方位角Ψ1、高低角Ψ2)通过坐标转换计算得出.因此,系统测量角度的误差δα,δβ,δγ 均由惯性导航系统和光电侦察平台中伺服系统的角度测量误差δθ 引入.
伺服系统采通过反馈光电编码器输出的脉冲数目用闭环控制方式来控制探测终端水平、俯仰等各个方向的转角,系统控制误差为±1 个脉冲.这个误差分量不随转角的变化而改变定值为δθ=±为光电编码器旋转一周输出的脉冲数)[6].
3.2 误差计算分析
为了便于计算,将式(1)至式(11)的公式模型这样表示:

综合上述误差来源分析可知本模型的速度误差分量有:激光测距仪的测距误差δL,载机速度的误差δSp,系统测量角度的误差δα,δβ,δγ,测速误差可以按照式(14)求得:

4 结 论
本文基于无人机的光电侦察平台,研究并提出了一种用于地面侦察的运动目标测速方法.首先分析了光电侦察平台及惯性导行系统可提供的可靠信息,然后阐述了本测速方法的原理并推导出数学模型,最后对于影响本测速模型精度的各个误差分量来源进行了简单的分析,推导出了误差计算的公式.由于目前无人机侦察领域对于运动目标光电测速的研究较少较浅,本文提出的测速方法也还不够成熟,需要进一步的完善.随着对光电测速技术的进一步研究探索,将会有更加科学有效、精度更高的测速方法模型得到开发.
[1] 王正林.无人机光电载荷及其应用[J].电讯技术,光电技术应用,2013,28(1):16-17.
[2] 柏青青,许建新,邵 慧,熊 智.无人机动态目标高精度定位方法研究[J].航空计算技术,2014,44(1):73-74.
[3] 樊邦奎,段连飞,赵炳爱等.无人机侦察目标定位技术[M].北京:国防工业出版社,2014.
[4] 孙明超,刘晶红,张葆.高帧频图像融合光学测量吊舱的设计[J].光学精密工程,2013,21(1):94-100.
[5] 毛昭军,汪的虎.姿态测量/激光测距的无人机目标定位模型[J].火力与指挥控制,2003,28(5):14-17.
[6] 张菊艳,吴桂林.激光测距的目标单点探测定位系统及定位误差分析[J].火力与指挥控制,2008,33(4):84-86.
