基于小波树和二维主元分析的人脸识别①

刘悦婷

(兰州文理学院电子信息工程学院，甘肃 兰州730000)

0 引 言

人脸识别是基于生物特征识别技术的身份认证中最主要的方法之一，对人脸识别方法的研究已成为当前模式识别和人工智能领域的一个热点［1］.人脸图像的维数非常高，且在高维空间中分布很不紧凑，不利于分类，计算的复杂度也很大.为获取人脸图像较紧凑分布，Kirby 和Turk 等首次把主元分析的子空间思想引入到人脸识别中，获得了较大成功.子空间分析的思想是根据一定性能目标来寻找一个线性或非线性的空间变换，将原始数据压缩到一个低维子空间，使数据在子空间中的分布更紧凑，使计算复杂度大大降低.因此本文将子空间分析中的二维主元分析法结合小波树进行人脸识别，ORL 和CAS－PEAL－R1 人脸库的实验结果表明，该算法对光照条件、脸部表情变化具有很好的鲁棒性，且能很好的重构人脸图像.

1 低频小波树

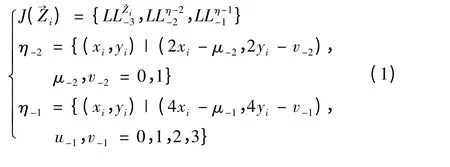
2 基于小波树和二维主元分析的人脸识别(WTMPCA)

2.1 二维主元分析

二维主元分析法以主元分析法(principal component analysis，PCA)为基础，不用把人脸图像矩阵转换成向量，而是直接用它求协方差矩阵，加快了特征提取速度.

训练集的协方差矩阵Gt的r 个最大特征值{λi|i=1，2，…，r}所对应的标准正交特征向量，即为训练集的最佳投影矩阵.若有图像样本，二维主元分析的最佳投影特征向量表示如式(4)所示，为图像样本量的主元(向量)，量→A 的特征矩阵量

2.2 分类器

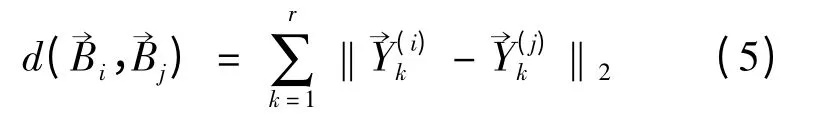
2.3 WTMPCA 算法

Step1:参数初始化，训练图像样本个数为M;

Step2:对人脸图像进行3 级小波分解后，形成低频小波树，如式(1)所示;

Step3:用式(2)将3 级小波系数进行线性变换;

Step4:用式(3)计算训练集的协方差矩阵，获得训练集的最佳投影矩阵;

Step5:用式(4)求取训练样本的特征矩阵;

Step6:用式(5)计算每个主元向量的欧式距离，若满足关系式(6)，则训练样本与测试样本是同一个人，否则不是;

Step7:判断训练样本个数是否完成，若完成，算法结束，否则返回Step5.

图1 人脸测试图像

图2 WTMPCA 与2D－PCA 识别性能比较

图3 WTMPCA 与2D－PCA 的Rank－N 识别性能比较

3 仿真实验

3.1 ORL 人脸库测试

为测试本文算法的有效性，选测试图像［6］如图1 所示，并与2D－PCA 方法比较.4 种测试模式(对每个人):(1)Subse1:前5 幅训练、后5 幅测试;(2)Subse2:后5 幅训练、前5 幅测试;(3)Subse3:在类中图像名编号为偶数的5 幅训练、剩余5幅测试;(4)Subse4:在类中图像名编号为奇数的5幅训练、剩余5 幅测试.

图4 WTMPCA 的识别性能

图6 人脸测试图像

从图2 可知，WTMPCA 人脸识别性能比2DPCA 方法好，尤其是在主元向量维数为1 时，WTMPCA 的识别率达到96%.图3 显示了WTMPCA和2D－PCA 的Rank－N 识别性能比较，选Subset1组测试，从图知随着“Rank”的增大，WTMPCA 和2D－PCA 方法的识别率都提高了，但WTMPCA 的识别率要比2D－PCA 方法高4%～5%，表明WTMPCA 能更好地聚类，改善算法的人脸识别性能.图4 和图5 显示了在不同ORL 训练组中的人脸识别性能，从图可知，只使用小波近似分量方法的识别性能大体上等效于使用了小波近似分量和小波细节分量的方法.这证明只使用小波近似分量的方法是合理的.因此，WTMPCA 只用了小波近似分量，而忽略了小波细节分量，节省了大量的计算时间.

图7 WTMPCA 与2D－PCA 受脸部表情影响比较

图8 样本不足WTMPCA 与2D－PCA 识别率比较

3.2 CAS－PEAL－R1 人脸库测试

选测试图像［7］如图6 所示，使用每个人任意三幅人脸图像做训练，剩余三幅做测试.从图7 可知，随着主元向量维数的增加，WTMPCA 人脸识别率保持不变，当主元向量维数为1 时，WTMPCA 的识别率为96%，而2D－PCA 最高人脸识别率为89.5%.因此WTMPCA 优于2D－PCA，对脸部表情变化具有很好的鲁棒性.图8 显示了在样本不足时两种方法识别率比较，图中“2”表示每个人有2 幅图像作训练样本，剩余4 幅图像作测试样本.当训练样本个数为1 时，WTMPCA 达到84%的识别率，当训练样本个数为4 时，WTMPCA 识别率达到97%.因此在样本个数不足时，WTMPCA 有很好的鲁棒性.

4 结 语

本文介绍了基于WTMPCA 的人脸识别算法，该算法应用小波多分辨率分解特性，分层次重组小波近似分量，最后使用二维主元分析进行人脸识别.由实验结果可知，该算法对光照条件、脸部表情变化具有很好的鲁棒性.实验测试中当主元向量维数为1 时，WTMPCA 方法的人脸识别率为96%.实验结果表明该算法对人脸的表情、光照及人眼睁闭具有良好的适应性，能很好的重构人脸图像.

［1］ ZHAO W，CHELLAPPA R，PHILIPS P J，etal.Face Recognition:a Literature Survey［J］.ACM Computing Surveys，2003，35(4):399－458.

［2］ 杨福生.小波变换的工程分析与应用［M］.北京:科学出版社，2000.

［3］ 朱希安，曹林.小波分析及其在数字图像处理中的应用［M］.北京:电子工业出版社，2012.

［4］ 曹林，陈登熠.基于小波近似分量非参数鉴别分析人脸识别算法［J］.北京信息科技大学学报(自然科学版)，2011，26(3):125－128.

［5］ 杨杰，黄朝兵.数字图像处理及MATLAB 实现(第2 版)［M］.北京:电子工业出版社，2013.

［6］ 杨军，袁红照.结合小波变换和图像主元分析的人脸识别［J］.计算机工程与应用，2010，46(4):1－3.

［7］ 杨军，张秀琼，高志升，等.用于人脸识别的两类主成分分析融合［J］.计算机工程与应用，2010，46(1):194－195，199.