高层结构等效线性化方法研究①

2015-04-13赖勤

佳木斯大学学报（自然科学版） 2015年1期

赖勤

(同济大学土木工程学院，上海200092)

0 引言

性能化抗震设计要求结构工程师对结构的弹性响应和弹塑性响应都能准确把握.目前，弹塑性时程分析是预测结构非线性响应的主要手段，但是弹塑性时程分析需要结构工程师具有较高的专业知识和软件应用能力，并且需要消耗较多的时间，因此在广大设计人员中不够普及.为了让设计人员易于得到结构的非线性响应，等效线性化方法应运而生，它通过将弹塑性结构的周期和滞回耗能进行等效，转化成线性分析，从而方便结构工程师的分析和设计.

以往对等效线性化方法的研究多集中于多层结构中［1～2］，其结果也表明等效线性化方法对多层结构的非线性响应的预测足够精确，可以满足工程需要.但是等效线性化方法在高层结构中的应用的相关研究较少，对以弯曲变形为主的高层结构，等效线性化方法能否准确预测其非线性响应，还需进一步研究.本文通过几个算例，对这方面进行了探讨.

1 分析方法

割线刚度法最先由Rosenblueth 和Herrera［3］在1964 年提出，它作为一种实用方法迅速推广开来，等效刚度由结构的最大响应确定，割线刚度就是等效刚度，从而可以确定等效周期:

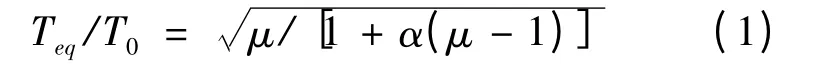
根据能量原则确定等效阻尼比:

式中:Teq为等效周期，T0为初始周期，μ 为延性系数，α 为屈服后刚度系数，ΔW 表示滞回耗能，即图1 中滞回环ABCD 的面积，W 为系统势能.

图1 双线性模型

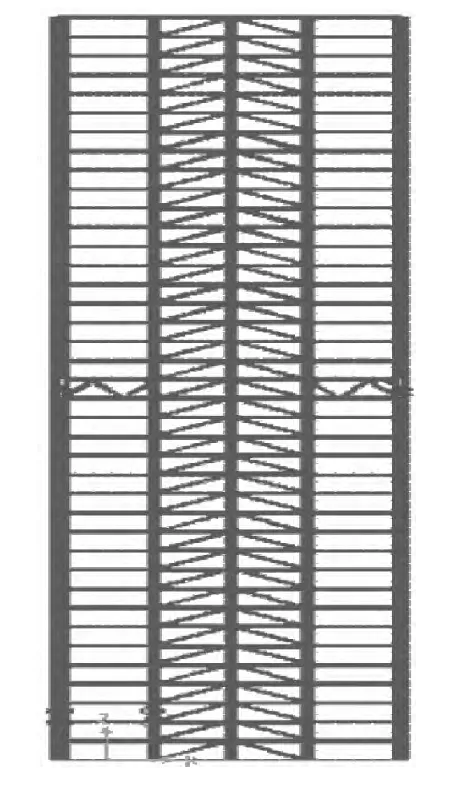
图2 BRCC－COS 结构模型

本文比较分析了2 种等效线性化方法(分别是我国规范建议的方法和采用割线刚度法的等代结构法)，为方便表达，本文分别将这两种方法称为规范法、等代SS 法.

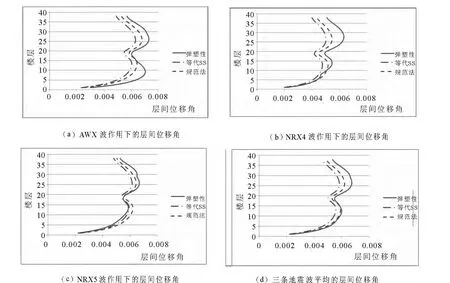
图3 BRCC－COS 结构层间位移角

图4 天津某实际工程模型

规范法的步骤［1］是:(1)用反应谱方法对结构响应进行预测，从而可以计算出阻尼器的响应、各层的弹性位移和水平地震力;(2)利用等效线性化方法确定阻尼器的等效刚度，进而得到结构的等效周期;(3)由1 的结果计算结构的应变能和滞回耗能，并利用能量关系得到结构的等效阻尼比;(4)用振型分解反应谱分析等效结构，从而计算出阻尼器的响应、各层的弹性位移和水平地震力;(5))重复(2)～(4)步，直至结构响应收敛，认为收敛的结果就是结构的弹塑性分析结果.

图5 天津某工程三条波的平均层间位移角

等代SS 法的步骤［4］是:(1)用反应谱方法对结构响应进行预测，从而可以计算出阻尼器的响应、各层的弹性位移和水平地震力;(2)阻尼器的等效刚度和等效阻尼比由割线刚度法确定;(3)有2 的结果集合得到整体结构的等效刚度矩阵和等效阻尼比;(4)用振型分解反应谱分析等效结构，从而计算出阻尼器的响应、各层的弹性位移和水平地震力;(5)重复(2)～(4)步，直至结构响应收敛，认为收敛的结果就是结构的弹塑性分析结果.

本文以弹塑性时程分析方法为依据，采用两个典型算例分析比较了上述2 种等效线性化方法在高层结构中的实际运用情况.

2 算例分析

2.1 BRCC－COS 算例

孙飞飞，邓忠良［5］等根据芯筒－刚臂结构的变形模式，将BRB(屈曲约束支撑)设置于刚臂和外柱处，提出新的芯筒－刚臂结构减震结构体系(简称BRCC－COS)，如图2 所示，39 层的芯筒—刚臂结构在19 层设有一道伸臂，在伸臂和外柱处设置BRB，在地震作用下，防屈曲支撑是预期的损伤耗能构件，屈服位移是4mm，屈服力是1200kN，结构构件尺寸如表1 所示.选用上海规程中建议的一条人工波和两条天然波，编号AWX，NRX4，NRX5，调幅至220gal，分别采用2 种等效线性化方法和动力弹塑性分析计算结构的地震峰值响应，结果如图3 所示:

表1 结构构件尺寸

2.2 天津某实际工程算例

天津于家堡某实际工程共63 层，291.6m，设有2 道伸臂，将伸臂处的斜撑替换为BRB(屈曲约束支撑)，共16 根，如图4 所示，BRB 屈服位移是5mm.选用上个算例同样的地震波，编号AWX，NRX4，NRX5，调幅至220gal，分别采用2 种等效线性化方法和动力弹塑性分析计算结构的地震峰值响应，结果如图5 所示:

从以上两个算例可以看到，在各条地震波作用下，等代SS 法和规范法二者精度相当，2 种等效线性化方法均能较为准确地预测结构的非线性峰值响应.与单条地震波的结果相比，多条地震波的等效线性化方法的平均结果误差更小，可以满足工程需要.