发动机排气歧管热模态分析及试验研究*

刘志恩，胡雅倩，颜伏伍，李党育

(1.武汉理工大学汽车工程学院，武汉 430070； 2.现代汽车零部件技术湖北省重点实验室，武汉 430070；3.西峡县内燃机进排气管有限责任公司，西峡 474550)



2015063

发动机排气歧管热模态分析及试验研究*

刘志恩1,2，胡雅倩1,2，颜伏伍1,2，李党育3

(1.武汉理工大学汽车工程学院，武汉 430070； 2.现代汽车零部件技术湖北省重点实验室，武汉 430070；3.西峡县内燃机进排气管有限责任公司，西峡 474550)

本文旨在探讨发动机的热负荷对排气歧管模态的影响。首先，在阐述模态分析理论的基础上，建立了排气歧管有限元模型，分别进行自由状态和承受螺栓预紧力的约束状态下的冷-热模态分析；接着构建模态试验系统，分别在自由状态和约束状态下进行排气歧管冷-热模态试验。最后，有限元模态分析和模态试验的结果对比表明，有限元模态分析的结果与试验结果基本吻合；螺栓预紧力的约束和热负荷都对排气歧管的模态产生影响，螺栓预紧力的约束使其固有频率显著提高，而温度升高则使固有频率稍有降低。

排气歧管；温度；热模态分析；模态试验

前言

随着工程中非线性问题的日益突出，理论模态和试验模态都是由线性向非线性的方向发展，由单纯的结构力学计算向多物理场耦合发展[1]。人们对模拟复杂工况下的结构模态进行深入的试验研究，以期提高模态分析的精度，扩大其应用范围。其中研究较深入的是与温度场耦合的热模态试验技术，它在航空领域也有较多应用。如20世纪50年代，美国的X-15验证机在大气层内以马赫数7飞行时，在高空中工作条件恶劣，由于结构表面受到强烈的瞬态气动加热作用，改变了其结构的固有特性而导致垂尾震颤。因而在实际工程设计阶段，须对在高温这类恶劣条件工况下的结构进行热模态的分析[2-4]。

发动机升功率的提高使关键零部件的热负荷不断增大。在汽车的排气系统中，排气歧管通过螺栓与缸体连接，它在工作过程中与高温废气直接接触，承受着从常温到近千摄氏度高温的冷热交变热负荷作用，在交变热负荷及排气的冲击下产生振动。因而研究螺栓预紧力和温度效应对排气歧管的振动特性的影响非常必要，对其结构的设计具有重要意义。

试验模态分析是为得到被测结构的模态参数，来对被测结构进行振动方面的评估，如结构的固有频率、阻尼比及模态振型等。热模态试验技术随着理论研究的深入而产生，并且受到一些与热相关领域的重视，但是真正实现模拟实际过程中热环境时，则受到一些试验手段等技术层面上的束缚。为此，美国的NASA Dryden飞行载荷试验室(DFRC)、俄罗斯的国家空气动力研究院等国家级的研究中心，国内的北京航空航天大学、北京强度环境研究所等研究中心，都针对热模态的试验技术及方法进行不断的探索与改进，目前已对一些简单并且可行的试验进行了分析，并证明了相关理论方法的正确性[5]。

本文中主要对排气歧管的热模态进行基础的试验研究。使用LMS数据采集设备对排气歧管的样件进行热模态试验，设计符合现有试验条件的合理热模态试验方案，并通过LMS Test.Lab软件对排气歧管的冷热模态进行动态测试及应用软件中模态参数的识别方法对测试数据进行后处理得到模态相关参数。通过与试验模态对比来对仿真分析的合理性和准确性进行分析。

1 模态分析理论

1.1 模态分析基本理论

假定结构的自由度为N，结构的动力微分方程[6]为

(1)

式中：[M]为质量矩阵(∈RN×N)；[C]为阻尼矩阵(∈RN×N)；[K]为刚度矩阵(∈RN×N)；{x}为N维的广义向量；{(f(t))}为节点载荷矩阵。结构系统的固有特性可由一组振动特征参数来进行定量描述，主要是固有频率及振型。

在忽略阻尼影响的情况下，其自由振动运动微分方程变为

(2)

自由振动可视为一系列的简谐振动的叠加，则令方程的解为简谐振动形式，即{x}={X}ejωt，其中{x}代表结构的主振型向量；ω代表圆频率，代入式(2)可得

([K]-ω2[M]){X}={0}

(3)

要使该方程具有非零解，唯一的条件是其位移的阻抗矩阵[Z]=[K]-ω2[M]的行列式为零，即

|[K]-ω2[M]|=0

(4)

ω1<ω2<ω3<…<ωN

(5)

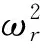
([K]-ω2[M]){φ}r={0}

(6)

该特征向量就是结构系统的模态向量，即振型向量。

1.2 最小二乘复指数法理论

试验模态分析的核心是模态参数辨识技术，辨识方法分为频域和时域两种。频域是以频响函数(传递函数)为基础的参数识别；时域是以时域信号(脉冲响应函数或自由振动响应)为基础的参数识别。本文中试验所用的是LMS Test.Lab 软件，采用最小二乘复指数法(LSCE)及最小二乘复频域法(LSCF)对模态各种参数进行识别。

最小二乘复指数法是一种多参考点的时域方法。它是目前一种常用的模态参数识别方法。设系统自由度的响应[7-8]为

(7)

(8)

式中：E为单位矩阵，维数为Ni×Ni，Ni为输入自由度数。设有2Nm个特征解(或极点)，则阶数p须满足：

p≥2Nm/Ni

(9)

[h(nΔt)]sE+[h((n-1)Δt)]sW1+…+

[h((n-p)Δt)]sWp=0

(10)

通过同时对所有的响应点考虑式(10)，便能够对矩阵系数W1,…,Wp进行整体的最小二乘法估计，通过得到的矩阵系数,即可将式(8)写为一般的特征值方程，求得pNi个特征值Zr，最后对极点λr和模态向量进行估计而得到所需的结果。

2 冷-热模态试验系统的建立

2.1 模态试验系统的组成

本试验中所用的模态振动测试设备如表1所示， 使用LMS Test-Lab 10软件中的Structures Analysis分析模块作为模态分析软件，试验台架布置如图1所示。

表1 热模态试验系统所用设备

如图1所示，模态试验的测试分析系统一般由3部分组成[9-10]。

(1)激励系统 施加动态激励信号，本试验中选用铝制缓冲头力锤，以激起高镍铸铁排气歧管的高阶频率。激励时应尽量使敲击力均匀，并使每次冲击位置和方向相对一致，避免缓冲头发生多次冲击或反跳现象而造成较大误差，根据监控图可对敲击的质量进行控制，以获得较精确的结果，便于进行信号的后处理[7]。

(2)同步数据采集系统(简称数采系统) 主要任务是将传感器采集到的位移、速度或加速度信号转换为数字信号，以便计算频响函数或功率谱等。本文中采用SISO(单输入单输出)法，通过对激励点和响应点信号同时进行高速采集，移动力锤的锤击点来获取数据。

(3)分析与后处理系统 模态分析软件及计算机工作站硬件等，用于进行模态参数识别，对信号进行分析和频响函数估计，最后得到如共振频率、阻尼比和模态振型向量等模态参数。

图2为现场试验台架图。试验中的测点应选择能准确全面体现结构整体轮廓，又方便测试的位置。激励点选在与振动模态节点位置有一定距离的地方，避免丢失模态。通过对有限元仿真结果的振型进行研究，选取高镍铸铁排气歧管样件的11个测点如图3所示，确保关键部位的节点能显示出振型，以便与有限元的仿真结果进行比较。由于结构较小，应考虑响应点安装传感器的方便性，并使其与结构连接紧密，以保证响应数据的准确性。热模态试验系统所用设备如表1所示。

2.2 试验方案的确定

为了与仿真数据进行对比，测试系统须与仿真分析尽量保持相同的边界条件。由于排气歧管在实车上的尾气排放温度可达800℃以上，而在试验中过高的温度会导致ICP传感器失效，为保证传感器的使用并达到使样件产生温度梯度的目的，模拟一定温度梯度的热环境，整体模拟温度较低[11-12]。表2为冷-热模态试验方案，图4和图5为冷模态自由及约束状态试验台架装置。

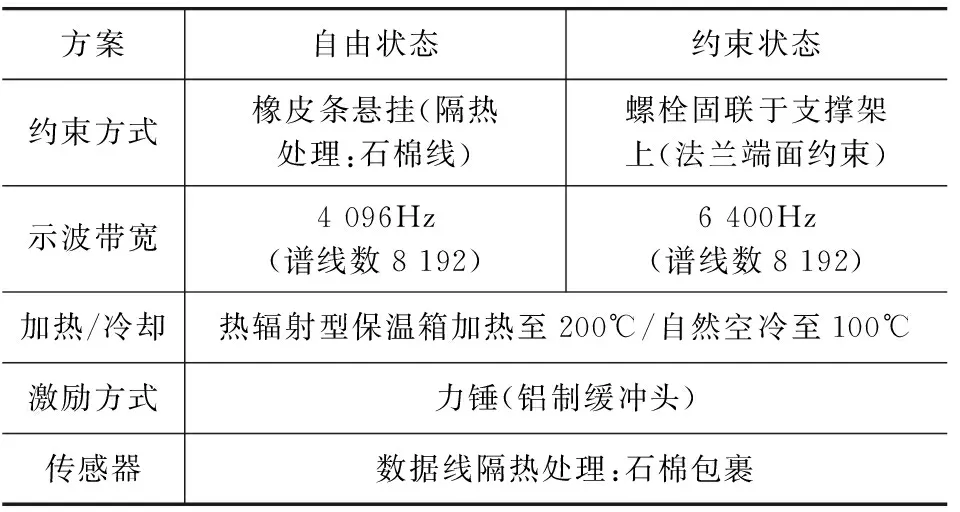
表2 冷-热模态试验方案

3 冷-热模态有限元分析

对汽油机的排气歧管进行常温状态下(即冷模态)的自由及约束状态振动特性分析，约束状态考虑螺栓预紧力的影响。然后对在温度效应作用下的排气歧管振动特性进行分析，即在加载螺栓预紧力的基础上进行热模态分析。

3.1 冷模态有限元分析

排气歧管的几何模型如图6所示，通过HYPERMESH软件划分网格，有限元网格单元数为548 863，局部加密。主要单元类型为四面体单元C3D4，得到有限元模型如图7所示。

冷模态即在常温作用下的恒定材料性能参数的模态分析。其中螺栓预紧力的大小为17kN，方向取Y轴负向。对于该排气歧管，选取材料为D5S(NiSiCr3552)，泊松比为0.283，密度为7 450kg/m3，常温下的弹性模量为125GPa，线胀系数为1.332×10-5K-1。冷模态有限元分析频率如表3所示，冷模态自由状态及约束状态振型分别如图8和图9所示。

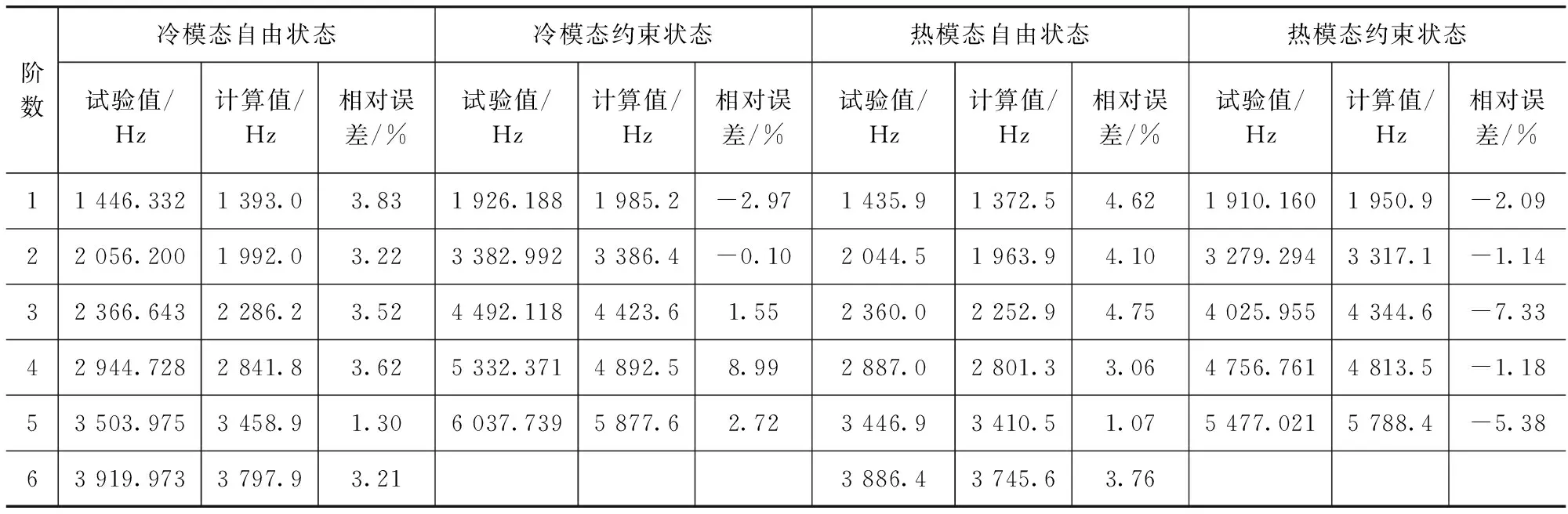
表3 冷-热模态试验值与计算值对比

约束模态在有螺栓预紧力作用下的第1阶固有频率为1 985.2Hz，主要变形是Z向的弯曲；第2阶的固有频率为3 386.4Hz，主要变形是X及Z向的弯曲；第3阶与第4阶的固有频率相近；第6阶与第7阶的固有频率相近；自由模态前10阶的振型都主要以弯曲为主。

3.2 热模态有限元分析

热模态即在不均匀温度作用下的加载随温度变化材料性能参数的模态分析。排气歧管材料基本参数与冷模态材料参数相同。在ABAQUS软件中建立随温度变化的非线性材料场作为材料属性，图10和图11分别为随温度变化的材料弹性模量和线胀系数参数。

考虑温度场和应力场影响的热模态有限元分析是以热分析和结构分析为基础，其基本流程如图12所示[13-14]。

(1)将温度边界作为分析的条件，在ABAQUS中进行热传导分析。

(2)以热传导分析的温度场为载荷，确定结构的热边界条件，结合随温度变化的材料物理性能和力学性能参数求解热应力。

(3)以热应力为初始应力条件，并考虑螺栓预紧力的加载及温度场的非均匀性，结合随温度变化的非线性材料物理性能和力学性能(密度、弹性模量、线膨胀系数和泊松比)，求解结构的热模态。

按照试验中的热环境温度，对排气歧管进行热模态有限元分析。首先在ABAQUS软件中进行热传导分析，设置内壁面的场温度为473K，外壁面的场温度为373K，壁面与空气的对流换热系数为13.5，单元类型为传热单元DC3D4。分析得到稳态的温度分布图如图13所示。由图可以看出，排气歧管温度范围在338.3～369K之间，最高温度出现在内壁面的出口处，与试验中的温度梯度大致符合。

通过ABAQUS得到试验状态下的热模态固有频率见表3。取自由状态及约束状态下前两阶的振型如图14和图15所示。

4 冷-热模态试验分析

4.1 冷模态试验结果

在排气歧管样件冷模态的试验过程中，经红外测温仪测得排气歧管温度为290K。通过测试和后处理，可以得到频率及振型结果。通过Modal Analysis模块进行后处理，将各极点的FRF(频率响应函数)进行sum，使用LSCE最小二乘复指数法来估计频率、阻尼、参与因子。得到自由状态及约束状态的频率稳态图如图16所示。

稳态图是通过LSCE法对极点频率、模态参与因子向量以及阻尼比进行一定公差范围内的对比得到。按照稳定性s>v>d>f>o进行模态的频率提取，得到前5阶的频率值见表3，将冷模态的试验频率结果与仿真结果进行对比，其中相对误差η可由公式：η=(ft-fA)/fA得到，式中ft指测量频率值，fA指计算频率值。

通过计算可以得到各阶频率的振型，冷模态试验的自由状态和约束状态1阶振型如图17和图18所示，其中实线代表未变形模型，虚线代表变形后的模型。

通过观察发现，由频率结果可以看出，误差大部分都在5%以内，具有较好的有效性。测得自由模态频率整体上比计算值大，约束状态的相对误差值有一定的上下浮动，这是由于约束状态测量结果中部分点的响应并不理想，在数据后处理中剔除部分由于二次锤击等造成的拟合稳定性不好的FRF数据，在通过LSCE法得到的集总频率有个别奇点，总体在误差的允许范围内。可以看出，冷模态有限元仿真与试验结果误差较小，说明排气歧管的有限元分析能够比较精准、合理地反映其实际动态特性。

通过冷模态试验振型可以看出，自由状态第1阶表现为Y/Z向的弯曲以及X向的扭转。约束状态第1阶表现为Y/Z向弯曲及X向扭转，与有限元分析结果中振型基本符合。

4.2 热模态试验分析

在排气歧管样件热模态的试验过程中，主要为保证传感器的使用，试验样件初始温度为473K，按照试验方案将样件冷却到内壁温度约为373K时开始进行试验。

根据测量数据得到稳态图，得到该排气歧管样件的前5阶测试频率和测量误差如表3所示，稳态图如图19所示。

冷-热模态的试验值对比图如图20所示。

通过软件后处理计算得到热模态试验的1阶振型图如图21和图22所示。

本文中对一定范围温度梯度的热模态进行了试验分析，并进行了相同热环境状态下的有限元分析，通过表3对比可以看出，自由状态下误差在5%以内，试验值整体上比计算值大，约束状态下的误差绝对值大多在5%以内，试验值整体上比计算值小。由于热环境下测量的不稳定性造成部分测点响应的不稳定，导致最后数据后处理得到的个别值吻合性不好，但总体上在误差允许范围内。

通过热模态试验振型可以看出，自由状态第1阶表现为Z向的弯曲和Y/Z向的扭转，约束状态第1阶表现为Z向弯曲和X向扭转，与相同条件下有限元分析的振型差别不大。对比冷-热模态的前两阶振型可以看出，不论是自由状态还是约束状态，两者的振型有部分变化，总体上温度对于扭转刚度的影响比弯曲刚度的大。

通过冷-热模态试验对比可以看出，热模态试验得到的自由状态下的频率整体比冷模态的有所降低，但降低的幅度不大；约束状态下的频率比冷模态的也有所降低，温度对于约束模态的影响比较大，并且温度对各阶的影响不同，其对高阶的影响较低阶的大。试验验证了有限元模型的精度及分析的准确性，对结构的有限元建模、分析具有指导意义。

热模态试验中产生误差的可能原因如下。

(1)仿真分析与测量方法的误差 仿真分析中没有考虑阻尼的影响，而试验中考虑了系统的阻尼等情况。

(2)锤击操作误差 在锤击激发过程中，由于样件的表面结构不规则，敲击点的位置不一定精确，以及二次锤击的产生，会对结果产生一定的误差。

(3)约束条件误差 试验中橡皮绳悬挂进行近似自由状态的模拟，而计算中歧管处于理想自由状态，造成边界条件的偏差；试验采用螺栓将排气歧管端面进行全约束，与仿真相比约束并不理想。

(4)热模态试验测量误差 热模态试验中存在热量散失，造成热环境的不稳定现象，会导致数据存在一定的误差；传感器的信号传递不稳定，部分点的响应并不理想，在数据后处理时，会导致集总平均后的频率及振型不太协调。

(5)环境因素 在测试过程中一定程度上受到环境中噪声等的影响。

由于设备以及试验条件的限制，对于较大温度梯度的热模态试验还不能进行模拟，只是将对应试验条件下的冷-热模态的试验结果进行对比分析，对于仿真结果具有一定的参考价值。

通过仿真与试验的验证可知，当结构实际应用中存在一定的温度梯度时，应考虑温度效应产生的材料非线性及预应力等对结构模态参数的影响。

5 结论

(1)在有限元分析中，考虑了温度及螺栓预紧力对排气歧管模态的影响，两者的综合因素使结构模型在受热后固有频率呈下降趋势，且对各阶的影响不同，随着阶数的增大影响增大，综合因素对排气歧管振型的扭转刚度比弯曲刚度影响大。

(2)排气歧管冷-热模态试验分析与有限元分析结果的对比可以看出，试验误差大多在5%以内，个别奇点除外，振型基本吻合，验证了有限元分析的准确性。由试验结果可见，一定的温度梯度对样件的模态产生影响，使其频率随升温而呈降低趋势。

在以后的排气歧管设计及评价中，应考虑螺栓预紧力、温度效应产生的材料性能变化及温度预应力等问题对结构动态性能的影响。

[1] 龙英，滕召金，赵福水．有限元模态分析现状与发展趋势[J]．湖南农机，2009,36(4):27-29．

[2] 程昊，李海波，靳荣华，等．高超声速飞行器结构热模态试验国外进展[J]．强度与环境，2012,32(3):52-59.

[3]SookYingHo,AllanPaull．CoupledThermal,StructuralandVibrationalAnalysisofaHypersonicEngineforFlightTest[J]．AerospaceScienceandTechnology, 2006,10: 420-426．

[4]ZhaoXiaoli，SunZhenxu，etal．CoupledFlow-thermal-structuralAnalysisofHypersonicAerodynamicallyHeatedCylindricalLeadingEdge[J]．EngineeringApplicationsofComputationalFluidMechanics2011,5(2):170-179.

[5] 任青梅．热/结构试验技术研究进展[J]．飞航导弹，2012(2):91-96.

[6] 张锴．预应力钢筋混凝土桁架梁动力实测及模态分析[D]．武汉：武汉理工大学，2010．

[7] 王卫华，杨转运，刘会．利用LSCE方法识别桥梁气动导数研究[J]．实验流体力学，2009,23(1):85-88．

[8]VerbovenP,CaubergheB,GuillaulneP.ImprovedTotalLeastSquaresEstimatorsforModalAnalysis[J].ComputersandStructures,2005,83(25-26):2077-2085.

[9] 陈林.基于试验模态分析的动车组动态设计研究[D].四川：西南交通大学，2009,6.

[10]EwinsDJ.ModalTesting:TheoryandPractice[M]. 2nd.NewYork:ResearchStudiesPressLtd，2000.

[11] 袁兰.模态分析技术及其软件的研发[D].杭州：浙江大学，2011,1.

[12]Hoon，MarkDzwonczyk,ErikGStraser,etal.AnExperimentalStudyofTemperatureEffectonModalParametersoftheAlamosaCanyonBridge[J].EarthquakeEngineeringandStructuralDynamics,1999(28):879-897.

[13] 纪科星，宋宏伟，黄晨光．温度场与应力场对主动冷却发动机振动模态的影响[C]．第三届高超声速科技学术会议．江苏无锡，2010，CSTAM-2010-0039．

[14] 李龙超，许涛．某柴油机排气歧管的热固耦合分析[J]．汽车工程师，2011(3):55-57．

Thermal Modal Analysis and Modal Tests of Engine Exhaust Manifold

Liu Zhi’en1,2，Hu Yaqian1,2，Yan Fuwu1,2& Li Dangyu3

1.SchoolofAutomotiveEngineering,WuhanUniversityofTechnology,Wuhan430070; 2.HubeiKeyLaboratoryofAdvancedTechnologyofAutomobileParts,Wuhan430070; 3.XixiaInternalCombustionEngineExhaustPipeCo.,Ltd.,Xixia474550

This paper aims at investigating the effects of the thermal load of engine on the vibration modes of exhaust manifold. Firstly after the theory of modal analysis is expounded, a finite element model for exhaust manifold is built and modal analyses in both normal and raised temperature conditions are conducted in free state and constraint state of bolt pre-tightening force respectively. Then modal test system is constructed and modal tests in both normal and raised temperature conditions are also performed in free state and bolt pre-tightening constraint state respectively. Finally the comparison between the results of finite element modal analysis and modal tests indicate that the results of finite element modal analysis are well agree with that of modal tests; both the thermal load of engine and the constraint of bolt pre-tightening force have obvious effects on the vibration modes of exhaust manifold: the natural frequencies of exhaust manifold significantly rise with the constraint of bolt pre-tightening applied, but they slightly fall with the increase in temperature.

exhaust manifold; temperature; thermal modal analysis; modal test

*中央高校基本科研业务费专项资金(2013-IV-024)资助。

原稿收到日期为2013年6月11日，修改稿收到日期为2013年8月19日。