0～3岁儿童颅骨轮廓统计分析*

葛 昊,李志刚,刘卫国，张金换

(1.清华大学，汽车安全与节能国家重点实验室，北京 100084； 2.浙江省汽车安全技术重点实验室，杭州 311228)



2015051

0～3岁儿童颅骨轮廓统计分析*

葛 昊1,李志刚1,刘卫国2，张金换1

(1.清华大学，汽车安全与节能国家重点实验室，北京 100084； 2.浙江省汽车安全技术重点实验室，杭州 311228)

本文提出了一种能够半自动地从医学CT图像中获取颅骨轮廓标志点的方法，快速准确地从54组儿童头部CT扫描数据中提取标志点，并通过主成分分析和回归分析，建立了儿童颅骨轮廓点集与儿童宏观参数(年龄和头部周长)之间的回归关系模型，并据之得出了6个月、18个月、36个月儿童头部轮廓形态的统计结果。结果表明，该模型可较好地预测给定宏观参数的儿童颅骨轮廓。

儿童颅骨轮廓；CT图像；主成分分析；回归分析

前言

对儿童造成致命和致残的损伤中，头部损伤是首要因素[1-2]。由于儿童的尸体实验较为稀缺，建立基于解剖学的有限元模型和开发高生物逼真度的假人是最为通用的研究手段；其中获取儿童头部形态的统计信息是上述工作的基础。

随着计算机断层成像技术(CT)和核磁共振技术(MRI)的成熟，人们对头部外形及其内部结构的形态研究越来越深入。国外已有一些研究机构对儿童大脑几何模型、儿童头部和颅骨形态特征等进行了研究，并得出了一定的统计规律[3-4]。

在儿童头部形态统计研究的过程中，一个必要的环节是从医学图像中提取出能够表征形态的标志点集合。区别于效率较低、精度较差的手工获取标志点的方法，本文中提出了一种能够半自动地从医学CT图像中获取标志点的方法和完整流程，使用该方法从54组儿童头部的CT扫描数据中分别提取出能够描述儿童颅骨轮廓的空间坐标点集，并进行了主成分分析和回归分析，建立了儿童颅骨轮廓点集与儿童宏观参数(年龄和头部周长)之间的回归模型。运用该模型生成了不同年龄、不同百分位的统计意义下的儿童颅骨轮廓，并与已有数据进行了对比验证，发现该模型比较准确。

1 儿童头部轮廓形态点集的建立

获取儿童头部CT扫描数据之后，依据图1所示的流程，从CT图像中提取出描述儿童头部轮廓形态的标志点。

1.1 儿童颅骨三维重现

从密歇根大学附属医院获取了60多个0～3岁年龄段且年龄接近均匀分布的儿童头部CT数据，去除有形态异常以及CT质量较差的几个，最终得到54个质量较好、儿童头部形态正常的CT数据。在样本进行CT扫描的过程中，由于机架倾斜角度的影响，每个样本CT数据的不同切片之间会有一定的角度偏移，直接进行三维重建后，样本会有严重的倾斜变形。所以，需对每一个头部CT进行机架倾斜矫正[5]，然后使用颅骨对应的阈值进行图像分割，并提取出骨骼组织；最后重建颅骨的三维模型并离散化为点云。上述机架倾斜校正和儿童颅骨的三维重现过程是在医学图像处理软件Mimics中完成的，重现过程如图2所示。

儿童颅骨的三维模型以离散点云的形式导出，但是导出的颅骨形态离散点分布是密集且无序的，数量也不确定，不能直接用于多个样本的统计分析。为获取可以进行统计分析的颅骨轮廓坐标点集，需要对上述离散点云进行规整处理。要求：(1)处理后的离散坐标点集中的坐标点数量和分布情况要能够比较准确地复现出儿童颅骨的轮廓形态；(2)不同的CT样本中提取出的坐标点集中的坐标点数量要一致，并且不同CT样本之间的坐标点要能够一一对应。

1.2 头部姿态校正

CT扫描过程中，每个儿童的头部姿态都不一样，生成的三维模型的姿态也各不相同，因此须要通过旋转和平移等操作符合统一的坐标系方向，以进行头部姿态的校正。

将上一步得到的儿童颅骨三维模型离散点云导入Geomagic Studio软件中进行处理。旋转头部模型使矢状缝平面平行于坐标系的y-o-z平面。通过头部解剖学形态点定义一个平面为基准平面，该平面由两个眼眶的最上沿和枕骨大孔[6]的上沿3个点组成；旋转模型使该平面平行于x-o-y平面，见图3。

1.3 分层获取头部轮廓

将上文提到的基准平面作为最低平面，将与基准平面平行且通过模型在z轴方向最高点的平面作为最高平面；在最高和最低平面之间等间距插入与其平行的48个平面，得到50个等间距且相互平行的平面。手工删除颅骨的内部轮廓，保留颅骨的外部轮廓曲面。用这50个平面去与模型做交集，其中z轴方向高度较低的49个平面将颅骨外廓面截成49条曲线，最高平面与模型相交得到一个点，记为点A。对49条曲线进行处理。

从Geomagic Studio中获取的外部轮廓曲线尚不能进行数学描述。为得到参数明确、便于处理的曲线，将每层颅骨外轮廓曲线离散为坐标点，并重新拟合成参数曲线。在常用的参数曲线中，三次样条曲线[7]便于计算，且能保证曲线上各点切线的斜率连续变化；同时三次样条曲线一定经过控制点(即上一步中离散得到的点)。故将其分段拟合为三次样条曲线，在Matlab软件中通过编写程序完成。

1.4 标志点的获取与对应

将上一步中得出的三次样条曲线重新离散，获取描述头部轮廓形态的标志点，统一各个样本的标志点个数，并建立一一对应的关系：在每层平面上，以通过最高点A为中心，从x轴正方向开始，以6°为间隔辐射状做射线，计算每条射线与上一步拟合出的三次样条曲线的交点，将每层平面上的60个交点添加到颅骨轮廓的坐标点集；将最高点A点添加到坐标点集；之后，统一各个样本坐标点集的原点。

在第1.2节中，已经对模型的姿态进行了校正，即规定了坐标系相对于模型的方向；在这一步中，要规定模型的基准位置，即规定坐标系的原点。对模型进行平移，将基准平面作为x-o-y平面，将每个样本坐标点集的几何中心点在基准平面的投影点作为坐标原点。这样所有的模型都具备相同的姿态和相同的基准位置。上述过程在Matlab软件中通过编写程序完成。

通过上述方法和对应流程的处理，从每个样本中提取出了2 941(60×49+1)个点作为表征该样本颅骨轮廓的坐标点集，这些点的坐标能够描述轮廓的形状。处理后的某个样本的结果如图4所示。

依次对每个样本都进行处理，得到54组表征颅骨轮廓的坐标点集；每个样本提取出的坐标点的个数都一致，且能根据层数和角度的二维索引建立一一对应的关系。

2 儿童头部轮廓统计回归模型的建立

2.1 主成分分析和回归方法

在本次研究中，样本个数n=54；每个样本由2 941个空间坐标点来描述，则每个样本的数据向量长度为l=2 941×3=8 823。所有样本点集构成的原始数据矩阵维数为54×8 823。如果对54个样本直接进行统计分析建立回归模型，计算量较大。为降低矩阵的维数，采用主成分分析的方法。

经过主成分分析，较少维数的数据就能够涵盖原始数据的绝大部分信息，即进行了降维处理。主成分分析之后，用降维后的数据可以近似还原原始数据。主成分分析的具体方法如下[8]。

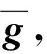
通过计算G的协方差矩阵的特征值和特征向量，G一定可以分解为

G=SPT

(1)

式中：S为主成分得分矩阵，其维数为n×l；P为矩阵G的协方差矩阵的特征向量构成的矩阵(特征值由大到小排列)，它是一个正交矩阵，维数为l×l，于是有

S=GP

(2)

矩阵G的协方差矩阵的前k个特征值之和与所有特征值之和的比值为前k个主成分的累积贡献率，表示前k个主成分包含原始数据信息的比例。当前k个主成分的累积贡献率足够大时，认为前k个主成分包含了原始数据的绝大部分信息，此时可以通过前k个主成分来近似矩阵G，近似的矩阵记为G*。

(3)

式中：Sk为矩阵S的前k列组成的矩阵，称为k主成分得分矩阵；Pk为矩阵P的前k列组成的矩阵。

(4)

式中：Ski为矩阵Sk的第i行构成的向量。

通过对式(4)分析发现，引起各个样本之间差异的因素只存在于Ski，即k主成分得分矩阵的第i行构成的向量。通过建立k主成分得分矩阵(因变量)与引起样本差异的宏观参数(自变量)之间的回归关系，即可通过宏观参数得到k主成分得分矩阵，进而得到对应个体的形态信息。

建立回归关系的方法如下[8]。

(5)

其中F=[f1,f2,…,fi,…,1]T

式中：C为待求的回归系数矩阵；F为所有样本的宏观特征参数(年龄和头部周长)构成的矩阵；fi为所有样本的第i个宏观特征参数构成的向量。

系数矩阵C可以用最小二乘法(LS)来求解：

(6)

求解出系数矩阵C后，给定一组宏观特征参数，可以基于式(5)求解出Ski，然后根据式(4)，与此宏观特征参数相对应的个体数据gi*也就确定。

2.2 儿童头部轮廓统计回归模型的建立和验证

上述主成分分析后，其累积贡献率随主成分个数的变化情况如图5所示。可以看出取前4个主成分就已经能代表原始数据90%以上的信息。

取k=1,4,12,50重构原始数据，对累积贡献率和重构误差(重构点到对应原始点距离的平均值)进行定量计算，结果如表1所示。

表1 不同主成分的累积贡献率和重构误差对比

式(6)，求解出系数矩阵C，建立50主成分得分矩阵与样本宏观参数之间的回归关系。根据此回归关系，给定一组儿童年龄和头部周长数据，利用式(5)和式(4)即可得到对应的儿童颅骨轮廓形态。这样儿童颅骨轮廓的统计回归模型就建立完成。以上过程通过编写程序在Matlab软件中自动实现。

为评价所建回归模型的准确程度，根据美国密歇根大学交通运输研究所(UMTRI)的研究报告[9]，从中选取了几组儿童年龄和头部周长的数据，利用该模型生成了对应儿童头部的轮廓，分别测量生成的头部轮廓的宽度，即头部最左点和最右点之间沿x方向的距离，再与UMTRI的测量数据进行对比。由于头部姿态校正方式的不同，模型头部宽度的测量方式是与UMTRI最为接近的，所以通过宽度来进行对比，结果如图6所示。从图中可以看出，本文的测量结果与UMTRI的测量结果比较相近，说明建立的模型较为准确，能够基本反映头部的生长特征。

3 儿童颅骨轮廓统计模型的应用

通过利用已建立的统计回归模型，在已知儿童的宏观参数(年龄和头部周长)的条件下来预测儿童颅骨三维轮廓形态。其中，儿童典型年龄段对应的50百分位的儿童头部周长是从美国疾病控制中心(CDC)公布的人体头部增长曲线[10]中获取，具体结果如表2所示。按照同样的方法，获取18月龄5百分位、50百分位和95百分位的儿童头部周长，结果见表3。

表2 特定年龄50百分位儿童头部周长

表3 18月龄不同百分位儿童头部周长

生成与表2和表3对应的儿童颅骨轮廓形态如图7和图8所示。可以看出，该模型不仅能够预测不同年龄儿童50百分位头部周长时的儿童颅骨三维轮廓形态，同时还能预测相同年龄时不同儿童头部周长的颅骨轮廓三维形态。

4 结论

提出一种从CT图像中半自动提取形态点集的方法。在对从CT中提取出的多组点集进行主成分分析和回归分析的基础上，建立了儿童颅骨轮廓形态与儿童年龄和头部周长的回归模型，从而可以通过儿童的宏观参数(年龄和头部周长)来预测对应的颅骨轮廓形态。方法和建立的儿童颅骨轮廓形态统计模型对于从医学图像中提取大量标志点、儿童头部有限元模型的建立和儿童假人头部的改进等有指导意义，为儿童头部的损伤研究提供形态基础。该方法还可拓展到人体的其它部位，如颈部和胸部等，可为更广泛的人体损伤研究提供依据。

[1] Li Z G, Hu J W, Reed M P, et al. Development, Validation, and Application of a Parametric Pediatric Head Finite Element Model for Impact Simulations[J]. Annals of Biomedical Engineering,2011,39(12):2984-2997.

[2] Li Z G, Hu J W, Reed M P, et al. Erratum to:Development, Validation, and Application of a Parametric Pediatric Head Finite Element Model for Impact Simulations[J]. Annals of Biomedical Engineering,2013,41(1):215-220.

[3] Danelson K A, Geer C P, Stitzel J D, et al. Age and Gender Based Biomechanical Shape and Size Analysis of the Pediatric Brain[J]. Stapp Car Crash J,2008,52:59-81.

[4] Loyd A M, Nightingale R, Bass C R, et al. Pediatric Head Contours and Inertial Properties for ATD Design[J]. Stapp Car Crash J,2010,54:167-196.

[5] Hu H. Tilted Gantry Image Correction for a Multislice Computed Tomography System: U.S. Patent 6,229,869[P].2001.

[6] 李瑞祥,周德明,张林,等.简明人体解剖彩色图谱[M].北京:人民卫生出版社,2001:10-13.

[7] 魏海涛.计算机图形学[M].北京:电子工业出版社,2007.

[8] Reed M P, Parkinson M B. Modeling Variability in Torso Shape for Chair and Seat Design[J]. ASME Conference Proceedings,2008:561-569.

[9] Schneider L W, Lehman R J, Pflueg M A, et al. Size and Shape of the Head and Neck from Birth to Four Years[R]. The University of Michigan Transportation Research Institute,1986.

[10] Centers for Disease Control and Prevention. 2000 CDC Growth Charts for the United States: Methods and Development[R]. Centers for Disease Control and Prevention,2002.

Statistical Analysis of 0～3-Year-Old Children Skull Contours

Ge Hao1, Li Zhigang1, Liu Weiguo2& Zhang Jinhuan1

1.TsinghuaUniversity，StateKeyLaboratoryofAutomotiveSafetyandEnergy,Beijing100084;2.ZhejiangKeyLaboratoryofAutomotiveSafetyTechnology,Hangzhou311228

A technique is proposed to semi-automatically acquire the marking points of skull contour from medical CT images, and with which marking points are quickly and accurately extracted from 54 sets of CT scanned data of children heads. Then by using principal component analysis and regression analysis, a regression relationship model between the skull contour point set and the macro-parameters of a child (e.g. age and head circumference) is established, and based on which the statistical results of 6-, 18-, and 36-month-old children head skull contours are obtained. It is shown that the model established can better predict the skull contours of children with given macro-parameters.

children skull contours; CT images; principal component analysis; regression analysis

*浙江省汽车安全控制技术重点实验室开放基金(LHY1307J00304)和中国博士后科学基金面上项目(2012M520252)资助。

原稿收到日期为2013年4月26日，修改稿收到日期为2013年9月28日。