基于ANSYS/LS-DYNA 的高强度钢丝缩径旋压过程应力应变分析
2015-04-09卢秀春
张 玮,卢秀春,刘 金
(燕山大学 机械工程学院,河北 秦皇岛 066004)
0 前言
高强度钢丝是一种技术含量很高的预应力钢材,在国内外已被广泛应用于凝土离心管桩、高架桥墩、高速铁路轨枕板等预应力构件中[1]。目前对钢丝两端外圆的加工所采用的方法是滚锻加工或切削加工,这种方法消耗人力和资源,噪声大,加工过程中的振动对人体有一定损伤。旋压技术作为一种先进的塑性成形工艺,适用于高强度、难变形的材料的加工[2-3],但其在小直径实心轴类件上的研究较少,本文采用计算机数值模拟的方法,结合旋压工艺对钢丝外圆缩径过程进行研究,描述成形过程中应力、应变分布规律,分析缩径成形的变形机理,为钢丝外圆旋压加工提供了新的方法和参考依据。
1 有限元模型的建立
为了简化计算和提高计算效率,只对钢丝长度的一部分进行建模,针对实际工况的复杂性和有限元模拟的局限性,做出如下假设:
1)钢丝采用光圆钢丝模型,且材质均匀,各向同性且不可压缩。
2)模拟计算时,忽略惯性力的影响和摩擦引起的温度的影响。
钢丝的主要材料参数如表1 所示。
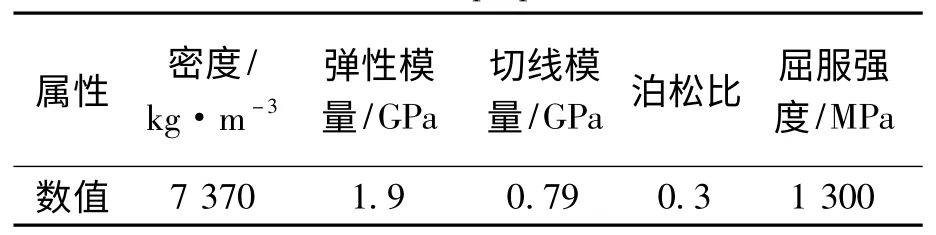
表1 钢丝的主要材料参数Tab.1 Main material properties of steel wire
钢丝直径为10.5 mm,转速为240 r/min,大旋轮直径为140 mm,小旋轮直径为40 mm,大旋轮与小旋轮的圆角半径都为8 mm,成形角都为25 ℃,进给比为0.5 mm/r,三旋轮中心相对钢丝中心呈122°和116°分布方式,三维模型如图1 所示。
钢丝将采用双线性强化模型,并用solid 164单元进行网格划分,端面网格尺寸设置为0.5 mm,轴向网格尺寸设置为0.3 mm,旋轮采用刚体模型,并用shell163 单元进行网格划分,网格尺寸设置为1 mm;接触设置将采用自动单面接触,设定旋轮为目标面,钢丝表面为接触面[4];模拟时钢丝设定为固定,旋轮绕钢丝的中心轴转动的同时沿着轴向进给运动,旋轮与钢丝之间摩擦采用常摩擦系数法,设定库伦摩擦系数均为0.1,为了避免模拟时产生振荡,导致计算终止,设置阻尼系数为20。
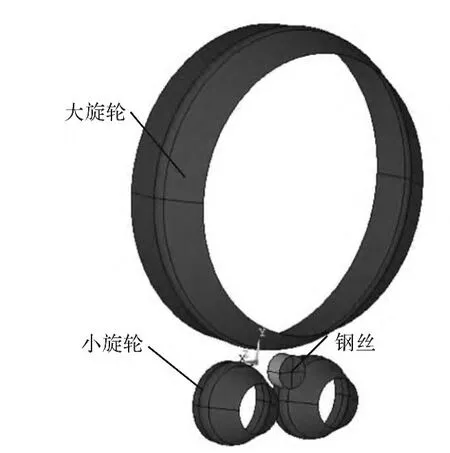
图1 实体模型Fig.1 Solid model
2 应力应变分析
图2为旋轮轴向进给4 mm 时钢丝的三向主应力分布图,由应力值和分布情况可以看出:旋轮与钢丝接触区的金属三向应力状态都为压应力状态,且接触区域金属所受到的压应力数值最大;第一主应力方向上,旋轮进给方向未接触的金属区域表面受到拉应力,进给方向相反的未接触金属区域表面受到压应力;第三主应力方向上,旋轮进给方向未接触的金属区域表面受到拉应力,其余的金属区域表面受到压应力作用;第二主应力方向上的分布情况与第一主应力方向分布相同。

图2 三向主应力分布Fig.2 Distribution of the three principal stress
图3 是旋轮轴向进给4 mm 时,钢丝在三维笛卡尔直角坐标系下三个方向上的应变分布,由图可以看出旋轮与钢丝接触区的金属在径向与切向方向上受到压应变,处于压缩变形,轴向受到拉应变处于伸长变形。在非接触区旋轮进给方向金属径向和切向受拉应变处于伸长变形,轴向受压应变,随着缩径过程的进行会造成旋轮前方金属的堆积隆起,后方金属受拉应变,拉应变的数值大于压应变,导致缩径过程中轴向伸长变形。
图4为旋轮与钢丝接触区横截面的三向应力分布图,从图中可以看出变形区域不仅限于钢丝的表面,钢丝的内部也有应力变化。x、y 方向上,旋轮压下形成的压应力区域越往钢丝内部值越小,钢丝内其他区域受到拉应力;轴向应力分布比较规则,其中旋轮之间区域表面受到拉应力作用,旋轮压下区域轴向受压,紧接着有一个压应力环状区域,与旋轮压下形成的压应力区域联通,再往钢丝内部有一层拉应力环状区域,在钢丝中心处有一小片区域受到压应力,形成了四个层次分布均匀的环状区域。
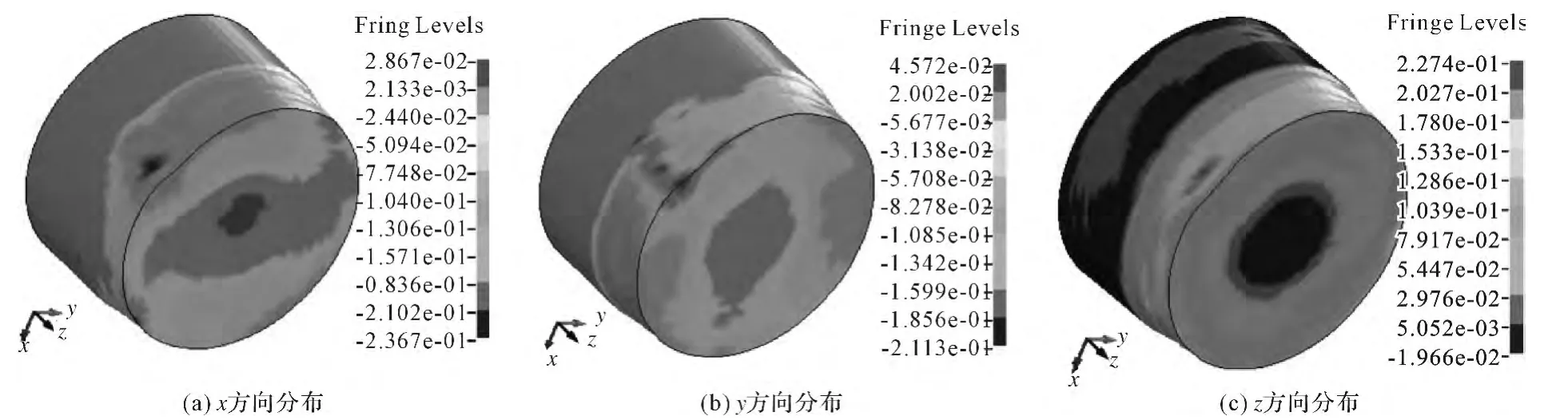
图3 三向应变分布Fig.3 Distribution of strain in three directions

图4 接触区横截面的应力分布Fig.4 Distribution of the cross section stress in contact zone
图5为旋轮与钢丝接触区横截面的轴向应变分布图,由图中可以看到,轴向应变为拉应变,钢丝轴向处于伸长变形,旋轮压下区域的拉应变值较大,越靠近钢丝中心部,其值越小,不同应变值形成了相应的环状区域,轴向应变分布跟轴向应力分布相似,比较规律,呈四个环状区域分布。

图5 接触区横截面轴向应变分布Fig.5 Distribution of the cross section strain along Z direction in contact zone
3 钢丝表面一单元应力应变分析
截取钢丝表面距离轴端2 mm 处一单元,查看其在缩径过程中的等效应力和等效应变分布情况,来反映出成形过程中钢丝的等效应力应变分布规律,更深入的研究缩径过程的变形机理。
图6 是缩径过程中该单元的等效应力与等效应变随时间的变化曲线,从图6a 可以看出,该单元在缩径过程中等效应力变化范围比较大,在0.5 s~1 s 内出现了周期性变化,等效应力峰值时刻说明该单元正处在旋轮与钢丝的接触区域,应力极小值时刻说明该单元没有与旋轮接触。1 s之后等效应力存在,说明旋轮继续轴向进给,钢丝轴向伸长,金属材料轴向流动,单元之间相互挤压产生应力变化,随着与旋轮距离的增大,所受到的等效应力值变化较小;从图6b 中可以看出该单元的等效应变随时间呈递增趋势,从刚开始到1.4 s 金属的等效应变增大,增长较快,主要由于受旋轮的挤压变形,1.4 s 之后随着缩径过程的进行,等效应变继续增大,材料流动变形量大,但变化速率逐渐减小,等效应变值趋于不变,成形较为稳定。
4 模型结果可靠性验证
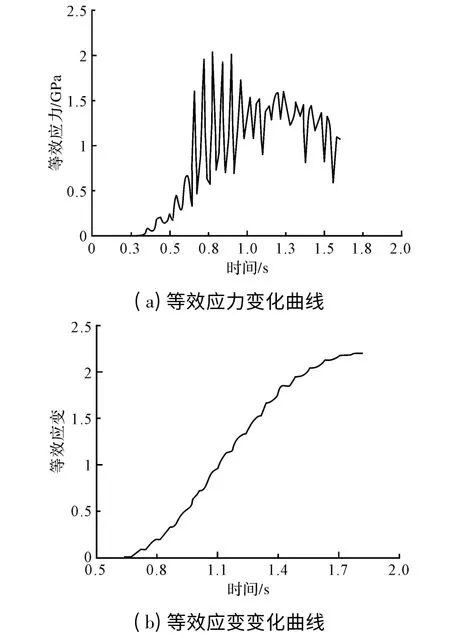
图6 钢丝表面一单元的应力应变变化曲线Fig.6 The stress and strain curve of a unit of outer surface
模拟计算过程中采用质量缩放技术可以有效的减少计算时间,但是缩放太大,容易影响计算的精度和收敛性[5]。图7为钢丝动能与内能的比值随时间的变化曲线,从图中可以看出,动能与内能的比值一直控制在0.025%之内;
另外模拟计算过程中采用Solid 164 单元划分网格时,容易激起“沙漏”模式,导致计算结果数值的震荡或者完全失真,图8 所示为沙漏能与内能的比值随时间的变化曲线,从图中可以看出,沙漏能与内能的比值一直控制在2.5% 之内,一般认为在模拟计算过程中钢丝动能与势能的比值较小,不超过10%,沙漏能不超过内能的5%~10%,计算结果是有效的[6]。因此本次仿真计算所建立的有限元模型是可靠的,结果是可信的。
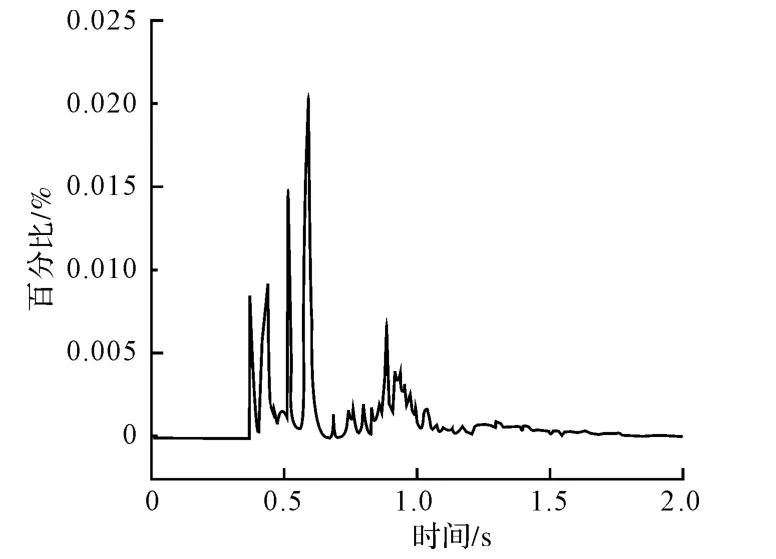
图7 动能与内能的比值变化曲线Fig.7 Ratio curve of kinetic energy and internal energy

图8 沙漏能与内能的比值变化曲线Fig.8 Ratio curve of hourglass energy and internal energy
5 结论
(1)应力分布规律。钢丝与旋轮的接触区三向应力状态为压应力状态;非接触区旋轮进给方向反向金属区域表面受压应力,进给方向金属表面区域受拉应力;接触区横截面轴向应力分布呈层次分布的环状,在径向和切向上,旋轮压下区域形成压应力,并越往钢丝内部值越小,其他区域受到拉应力。
(2)应变分布规律。旋轮与钢丝接触区的金属在径向与切向方向上受到压应变,轴向受到拉应变,在非接触区旋轮进给方向金属径向和切向受拉应变,轴向受压应变,进给方向反向金属受拉应变;接触区横截面轴向受拉应变,并呈分布层次规律的应变环,越往轴中心应变值越小。
(3)钢丝缩径成形的变形机理为钢丝与旋轮接触区金属径向与切向被压缩,沿轴向流动,随着旋轮轴向进给,轴向方向离旋轮距离越远的金属区域变形量越大,但变形速率越低,成形过程是钢丝整体参加塑性变形且连续变化的过程。
(4)钢丝外圆表面所形成的应力状态符合工程使用要求,对应用旋压工艺加工小直径轴类件方面提供了理论参考,同时对钢丝外圆旋压加工具有一定的参考价值。
[1]周和敏,左铁镛,易长森,等.高强度预应力螺旋肋、螺旋槽钢丝的研制[J].北京工业大学学报,2000,26(2):30-34.
[2]赵云豪,李彦利.旋压技术与应用[M].北京:机械工业出版社,2008.
[3]张涛 旋压成形工艺[M].北京:化学工业出版社,2009.
[4]梅瑛,李瑞琴,张晨爱,等.筒形件强力反旋的数值模拟及旋压力分析[J].机械设计与研究,2007,23(4):65-68.
[5]祖汪明,束学道,彭文飞.质量缩放技术在楔横轧有限元模拟中的应用[J].冶金设备,2008(3).
