一道预赛题的“简解”与“反思”

●盛耀建(湖州中学浙江湖州313000)

一道预赛题的“简解”与“反思”

●盛耀建(湖州中学浙江湖州313000)

笔者最近在研究2013年全国高中数学联赛山西省预赛试题时发现:试卷中的第11题(最后一题)有2种更为简单的求解方法，由此引发对此题的进一步深入探究，现将思考过程展示如下:

1 题目

例1盒中装有红色和蓝色纸牌各100张，每色纸牌都含标数为1，3，32，……，399的牌各1张，2色纸牌的标数总和记为S.对于给定的正整数n，若能从盒中取出若干张牌，使其标数之和恰为n，便称为一种取牌n－方案，不同的n－方案种数记为f(n).试求f(1)+f(2)+…+f(S)之值.

2 简解

结合文献［1］中的2种求解方法，笔者经过研究得出以下2种更为简单的解法.

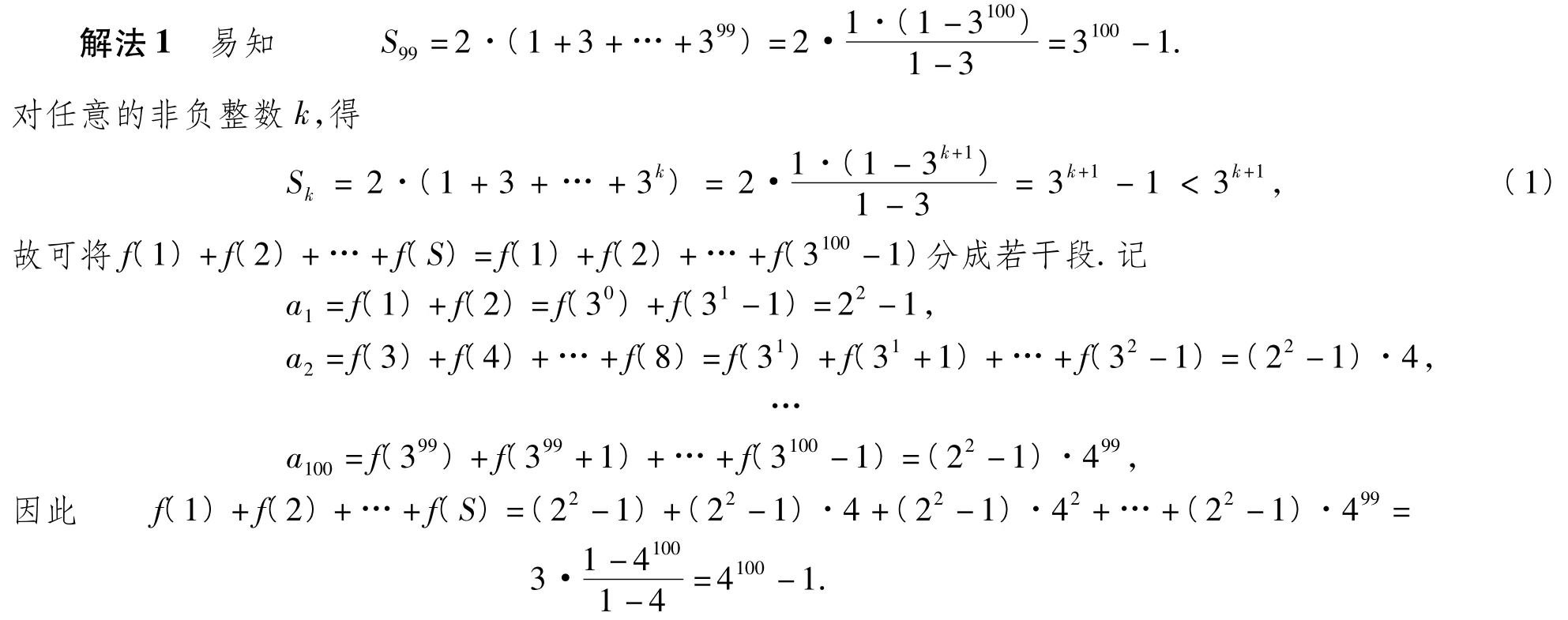
说明此解法以构成m(其中m=1，2，…，S)的1，3，32，…，399中次数最高项为标准进行分类，即:由式(1)可知，若能从盒子中取出若干张纸牌，使其标数之和为3k－1，3k－1+1，…，3k－1等，则取出的纸牌中最大的标数必为3k－1(其中取法有22－1=3种)，而标数小于3k－1的纸牌可任意(其中取法共4k－1种)，故由分步乘法计数原理得

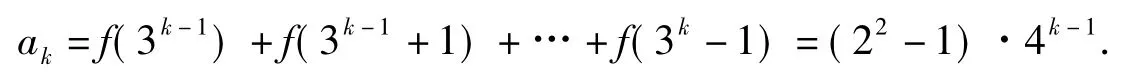
解法2因为无论取多少纸牌、取哪些纸牌，这些纸牌的标数和都不会超过S且每张纸牌不同，所以无需考虑f(m)(其中m=1，2，…，S)的具体值，而只需要关注从2n张纸牌中取出若干(大于0)张纸牌有几种取法即可，注意到标数为3k(其中k=0，1，…，S)的这类纸牌的取牌种类有4种，故f(1)+f(2)+…+ f(S)=4100－1(其中1表示取0张纸牌的取牌种类).

说明“解法2”在深刻分析了题意后，准确地把握了问题的本质，由分步乘法计数原理迅速得出正确答案，堪称“秒杀”，大大降低了试题的压轴性.

3 反思

题目在“解法2”的映衬下，变得过于简单，失去了其作为竞赛题的“高大上”，也不符合编题者的编题意图，不免让人感到有点可惜.因此，笔者作了进一步的研究，发现不改变题设条件，仅适当改变问题形式，即可挽回题目的价值，达到增强压轴效果，“改编”过程如下:

改编题例1中题设条件不变，问题改为“试求f(1)+f(2)+…+f(1 000)之值.”

解由1 000=36+35+33+1，知

评注将“S”改为“1 000”，在问题的设计上作了小的改动，因其不可再直接用“解法2”的方法求解，看似数据减小，实则试题难度不降反升.需利用“解法1”中“以构成m的1，3，32，…，399中次数最高项为标准进行分类”的思想将1 000改写为36+35+33+1，及结合“解法2”的巧妙计算方法即可求出答案，改编后的试题在解题思路的布局上有了“延伸”，更具回味性.

4 结论

笔者对1 000这一数据进行了进一步的探究，得出了更一般的结论:

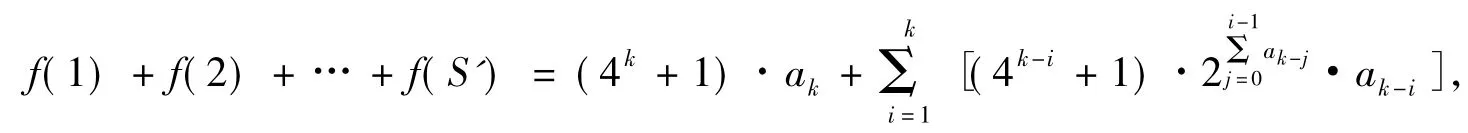
其中S'=a0·1+a1·3+a2·32+…+ak·3k，ai∈{0，1}，i=0，1，2，…，k.

当S'=a0·1+a1·3+a2·32+…+ak·3k中某些ai=2时，可以通过逐步调整系数2的位置降低计算量，但情况还是比较复杂，在此不再展开赘述.有兴趣的读者可以尝试求f(1)+f(2)+…+f(65)之值(注:65=2·33+32+2).

［1］中国数学会普及工作委员会组编.2014年高中数学联赛备考手册(预赛试题集锦)［M］.上海:华东师范大学出版社，2014.