一类数列与导数压轴试题命题手法揭秘
2015-04-05杨苍洲泉州市第五中学福建泉州362000
●杨苍洲(泉州市第五中学福建泉州362000)
一类数列与导数压轴试题命题手法揭秘
●杨苍洲(泉州市第五中学福建泉州362000)
再次研究2011年湖南省数学高考理科压轴试题,解完该试题,一直感觉意犹未尽.笔者思考:此类试题是如何命制的呢?洞悉命题手法是否有助于解题呢?借助此命题手法,是否可以依法炮制出相同类型的试题呢?
1 命题手法探究
例1已知函数f(x)=x3,
1)求函数h(x)=f(x)-g(x)的零点个数,并说明理由;
2)设数列{an}(其中n∈N*)满足a1=a(其中a>0),f(an+1)=g(an),证明:存在常数M,使得对于任意的n∈N*,都有an≤M.
(2011年湖南省数学高考理科试题)
让我们结合函数的图像来探究问题的本原.
首先作出函数f(x)=x3,的图像(如图1所示).从图1我们可以看出,当x≥0时,函数f(x)与g(x)有2个交点,其中一个横坐标为0,另一个记为x0.因此,h(x)=f(x)-g(x)的零点有2个,其中一个为0,另一个为x0.
问题1)的编制正是基于上述事实.

图1

图2
如图2,当a1=a∈(0,x0),过点A1(a1,g(a1))作y轴的垂线,交函数f(x)的图像于点B1(a2,f(a2)),显然g(a1)=f(a2);过点B1作x轴的垂线,交函数g(x)的图像于点A2(a2,g(a2)),再过点A2作y轴的垂线,交函数f(x)的图像于点B2(a3,f(a3)),显然g(a2)=f(a3)……按照此规律依次作图,从图2可以看出,满足条件f(an+1)=g(an)的数列{an}单调递增,且an∈(0,x0).同理,当a1=a∈[x0,+∞)时,可结合图像构造出满足条件f(an+1)=g(an)的数列{an},且{an}单调递减,an∈(x0,a].因此,存在常数M= max{x0,a},使得对于任意的n∈N*,都有an≤M.
问题2)的编制源于上述图像所呈现的数列规律.
2 命题手法对解题的启示
在问题1)的求解过程中,大部分解题者采用了下述方法:

当x∈(0,+∞)时,h″(x)>0,因此h'(x)在(0,+∞)上单调递增,则h'(x)在(0,+∞)内至多只有1个零点.又因为h'(1)>0,,则内有零点,所以h'(x)在(0,+∞)内有且只有1个零点.记此零点为x1,则当x∈(0,x1)时,h'(x)<0,h(x)单调递减,而h(0)=0,从而h(x)在(0,x1]内无零点;当x∈(x1,+∞)时,h(x)单调递增,又因为

所以h(x)在(x1,+∞)内有且只有1个零点.
综上所述,h(x)有且只有2个零点.
上述解法相对繁琐.其实,在问题1)的探究过程中,若能结合函数图像,则能观察出:函数h(x)的零点有2个,其中一个为0,另一个为x0>0.因为,记,所以只需证明φ(x)有且只有1个零点.又因为,当x∈(0,+∞)时,φ'(x)> 0,所以φ(x)在(0,+∞)上单调递增.由
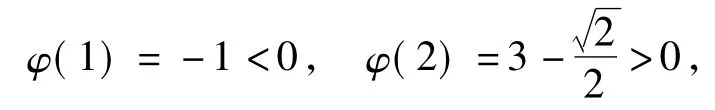
知φ(x)在(0,+∞)内有且只有1个零点.
综上所述,h(x)有且只有2个零点.
由于问题2)的抽象性与交汇性,使得试题的难度陡然增大,大部分学生的探究活动无法继续.实际上,若能洞悉命题者的命题手法,居高临下地审视试题,则能预知所求数列{an}应满足:当a1= a∈(0,x0)时,{an}单调递增,且an∈(0,x0);当a1=a∈[x0,+∞)时,{an}单调递减,且an∈(x0, a](其中x0为函数h(x)的正零点,即.因此,问题2)的求解需分2类情况进行讨论.
由此猜测:当a<x0时,an<x0.下面用数学归纳法证明:
①当n=1时,a1<x0显然成立.
②假设当n=k(其中k≥1)时,有ak<x0成立,则当n=k+1时,

从而ak+1<x0.故对任意的n∈N*,an<x0成立.
同理可猜测:当a≥x0时,an≤a.下面用数学归纳法进行证明:
①当n=1时,a1≤a显然成立.
②假设当n=k(其中k≥1)时,有ak≤a成立,则当n=k+1时,
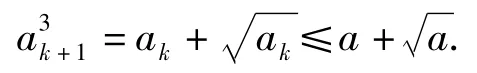
由第1)小题知,h(x)在(x0,+∞)上单调递增,得

得ak+1≤a.故对任意的n∈N*,an≤a成立.
综上所述,存在常数M=max{x0,a},使得对于任意的n∈N*,都有an≤M成立.
3 基于此手法的试题命制
学习了上述命题手法,笔者尝试进行试题命制,经过努力,得题如下:
例2已知函数f(x)=ln(x+1).
1)求函数f(x)在x=0处的切线方程;
2)设数列{an}(其中n∈N*)满足an+1= f(an),证明:数列{|an|}(其中n∈N*)单调递减.
分析1)略;
2)若a1>0,下用数学归纳法证:an>0.
①当n=1时,a1>0.
②设当n=k时,ak>0.又因为ak+1=f(ak)= ln(ak+1),所以ak+1>0.
由①②可得,对于任意n∈N*,an>0.此时|an|=an,于是
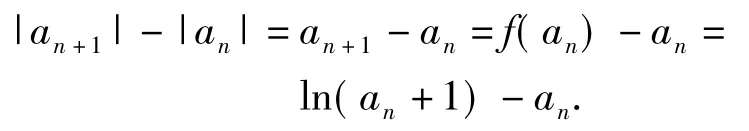
令g(x)=ln(x+1)-x(其中x>0),则

从而g(x)在(0,+∞)上单调递减,于是
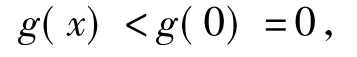
即当x>0时,ln(x+1)<x.又an>0,因此

从而数列{|an|}(其中n∈N*)单调递减.同理可证,当a1<0时,数列{|an|}(其中n∈N*)单调递减.
综上所述,数列{|an|}(其中n∈N*)单调递减.
例3已知函数f(x)=ex,g(x)=cx+1.
1)若函数f(x)的图像恒在函数g(x)的图像的上方,求k的值.
2)当c=2,设数列{an}(其中n∈N*)满足f(an+1)=g(an).试问是否存在常数M∈(1,2),当a1∈(0,M)时,恒有an∈(0,M)(其中n∈N*).若存在,请写出M满足的关系式;若不存在,请说明理由.
分析1)略;
2)存在满足题意的实数M,实数M应满足

先证方程(1)有且仅有1个解.令h(x)=ex-(2x+1),则
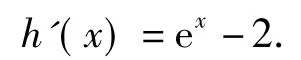
当x∈(1,2)时,h'(x)>0,h(x)单调递增.又因为h(1)=e-3<0,h(2)=e2-5>0,所以h(x)在(1,2)有且只有1个零点,即存在唯一实数M∈(1,2)使得方程(1)成立.
下用数学归纳法证明:当eM=2M+1,a1∈(0,M)时,恒有an∈(0,M)(其中n∈N*).
①当n=1时,a1∈(0,M).
②设当n=k时,ak∈(0,M).因为f(ak+1)= g(ak),所以eak+1=2ak+1.又ak∈(0,M),从而

即eak+1∈(1,eM),因此ak+1∈(0,M).
由①②可得,当a1∈(0,M)时,恒有an∈(0,M)(其中n∈N*).
