判断法向量的方向准确求解二面角
2015-04-05裘春风鄞江中学浙江宁波315151
●裘春风(鄞江中学浙江宁波315151)
判断法向量的方向准确求解二面角
●裘春风(鄞江中学浙江宁波315151)
利用空间向量法求证空间位置关系及空间角已为大家所熟知.利用法向量公式求出余弦值后,仅仅通过观察和凭直觉来判断,有时不能确定究竟是钝二面角还是锐二面角(二面角的余弦值是正的还是负的).事实上,笔者在课堂上也陷入了同样尴尬的局面.对于学生提出来的“怎样正确判断是钝二面角还是锐二面角”这一问题,也没有提供完美的答案.课后,笔者对这一问题作了思考,查阅了相关的文献,并对文献中提供的各种方法和途径作了分析、比较.笔者认为,可以通过确定法向量的方向来准确求解二面角的大小.

图2
首先,认识法向量的夹角和二面角的关系.法向量的方向指向二面角的内部,称之为“进”入半平面;法向量的方向指向二面角的外部,称之为穿“出”半平面.如图1,当法向量n1,n2“一进一出”时,n1,n2的夹角就是二面角的大小.如图2,当法向量n1,n2“同进同出”时,n1,n2的夹角就是二面角的补角.因此,可简单地归纳成“法向量同进同出,角互补;法向量一进一出,角相等”.
其次,如何正确判断法向量是“进”入半平面还是穿“出”半平面呢?下面笔者举例说明.
例1已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是平行四边形,∠BAD=120°,PA=AD=1,AB=2,M,N分别是PD,CD的中点.
1)求证:MN⊥AD;
2)求二面角A-MN-C的平面角的余弦值.
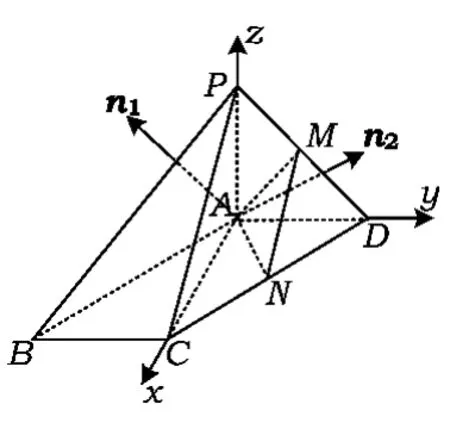
图3
分析1)略.
2)以A为坐标原点、AC,AD,AP所在直线为坐标轴,建立如图3所示的空间直角坐标系,则A(0, 0,0),,D(0,1,0),P(0,0,1),,从而

点评此时凭直觉很难确定二面角A-MN-C的平面角是钝二面角还是锐二面角.其实,可以通过判断法向量的方向,如平面AMN的法向量的方向是“进”入半平面AMN,平面CMN的法向量的方向是穿“出”半平面CMN.因此,根据“法向量一进一出,角相等”原则,可以确定二面角A-MN-C的平面角的余弦值为.
例2在三棱柱ABC-A1B1C1中,已知,BC=4,BC的中点为O,A1O⊥底面ABC.
1)证明:在侧棱AA1上存在一点E,使得OE⊥平面BB1C1C,并求出AE的长;
2)求二面角A1-B1C-B的平面角的余弦值.
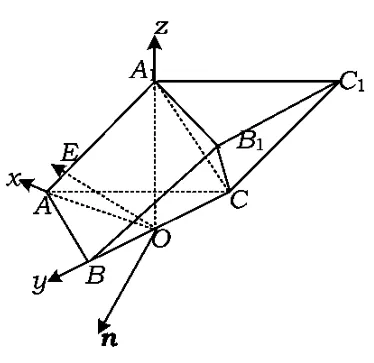
图4
分析1)略.
2)如图4所示,分别以OA,OB,OA1所在的直线为x,y,z轴建立空间直角坐标系,则A(1,0,0),C(0,-2,0),A1(0,0,2), B(0,2,0).由第1)小题可知,则点E的坐标为,从而平面BB1C1C的法向量是.
设平面A1B1C的法向量为n=(x,y,z),由得
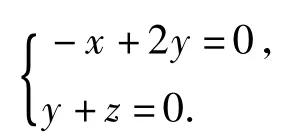
令z=-1,得x=2,y=1,即n=(2,1,-1),从而

点评可以判断“进”入半平面BB1C1C,法向量n也是“进”入半平面A1B1C,根据“法向量同进同出,角互补”原则,可以确定二面角A1-B1C-B的平面角的余弦值为
一般地,一个平面的法向量总有一个明显的方向,先求出法向量,根据法向量的值在图形中标出法向量大致的方向;然后通过判断法向量是“进”入或者穿“出”某个半平面;再根据“法向量同进同出,角互补;法向量一进一出,角相等”的原则,从而准确求解二面角的大小.
有了上面的理论和实践,笔者给学生上了一堂专题课“判断法向量的方向,准确求解二面角”.终于,较完美地回答了学生的问题,解决了学生的困惑.
[1]齐相国.法向量求二面角时法向量的方向的判断方法[J].数学通讯,2009(4):22-23.
[2]李伟.再谈用法向量求二面角之难点——兼与《利用法向量求二面角的一个难点》一文的商榷[J].中小学数学:高中版,2009(5): 20-22.
[3]黄辉.选择法向量的方向,准确求解二面角[J].中学数学研究,2010(7):41-42.
