一道高考题的解法探究*
2020-02-12佘军仁陈巧红
■佘军仁 陈巧红
例题(2016年全国Ⅲ卷)定义“规范01数列”{an}如下:{an}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,ak中0 的个数不少于1 的个数。若m=4,则不同的“规范01数列”共有( )。
A.18个 B.16个
C.14个 D.12个
答案:C
探究一、用分步计数原理
解:由题意,{an}中共有8项,4项为0,4项为1,且第一项为0,第八项为1,且要符合对任意k≤2m,a1,a2,…,ak中0 的个数不少于1的个数。如图1 所示,此时可按项数从小到大分步作答,但关键是只要前面出现3个0,即结束讨论,分步如下。

图1
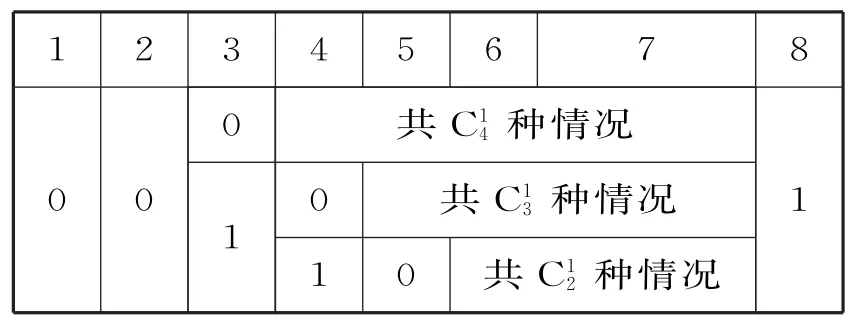
图2
(2)当第二项为1时,第三项只能为0,当第四项为0 时,共种情况;当第四项为1时,第五项只能为0时,共种情况。如图3。
探究二、用分类计数原理
解:由题意,{an}中共有8项,4项为0,4项为1,且第一项为0,第八项为1,且要符合对任意k≤2m,a1,a2,…,ak中0 的个数不少于1的个数,分为以下几种情况:
(1)前4项均为0,后4项均为1——共1种情况;
(3)前4项2个0,2个1,后4项2个0,2个1——共2×2种情况。
所以,共有1+9+4=14(种)情况。
探究三、构造路径问题,通过标数法解题
解:在直角坐标系下,若向右走1个单位代表0,向上走1个单位代表1,该题可转化为在4×4方格y≤x的区域内,从O点走到A点的最短路径的条数。如图4 所示,给经过的每一个格点(i,j)[数学上把在平面直角坐标系中横纵坐标均为整数的点称为格点(latticepoint)或整点]标数,数字为从O点到点(i,j)的最短路径条数,除y=x上格点(i,i)标的数字和格点(i,i-1)相同外,其余y<x的区域内格点(i,j)上标的数字为格点(i-1,j)与格点(i,j-1)上标的数字之和,可得最后到达A点最短路径的条数为14种。
注:图4 中标在y=x上格点的数字又称为“卡特兰数”。
进一步归纳:
定义“规范01数列”{an}如下:{an}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,ak中0的个数不少于1的个数,则不同的“规范01数列”共有个。
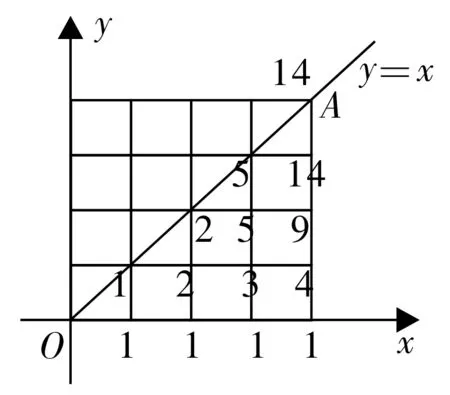
图4
