定向图弧连通度的下界

王晓丽，张国志

（晋中学院数学学院，山西晋中030619）

（编辑 郭继荣）

0 引言

本文讨论有限无环无重弧的有向图.用V＝V（D）和A＝A（D）分别表示有向图D的顶点集和弧集，且n用分别表示D的顶点数（或阶）和弧数.如果xy∈A（D ），称x控制y，并称x为这条弧的尾，y为这条弧的头.设X和Y是V（D）的两个不相交的顶点子集，用（X，Y）表示尾在X中，头在Y中的所有弧组成的集合.由x控制的所有顶点组成的集合称为顶点x的外邻域，记为N+（x）；由控制x的所有顶点组成的集合称为x的内邻域，记为分别是x的外度和内度.顶点x的度d.用 δ+和 δ-分别表示D的最小外度和最小内度，D的最小度 δ＝min.D的度序列定义为顶点度的不增序列

如果D的任意两个不同的顶点u、ν，在D中都存在（u，ν ）-路，则称D为强连通的.对于强连通有向图D，若弧集S⊆A（D），D-S不是强连通的，则称S是D的一个弧割．弧数最少的弧割称为最小弧割.D的最小弧割中弧的条数称为D的弧连通度，记为 λ（D）.由定义显然 λ（D）≤δ（D）.当 λ（D）＜δ（D ）时，称有向图D是非极大弧连通的.本文未给出的术语和记号请参见文[1]．

1 主要结论

定义1 设D是一个有t个强连通分支的有向图.令D1，D2，…，Dt是D的t个强连通分支排成的序列.若对于任意的uν∈A（D），u∈A（ Di），ν∈A（ Dj），总有i＜j，则称上面的序列为D的一个强连通分支无圈序.

定义2 对于有向图D，去掉D中弧的方向，再去掉产生的重边得到的简单图称为有向图的基础图，记为UG（D）．

定义3 如果有向图D的基础图不含p+1阶的完全子图，称D的团数ω（D ）≤p．

定义4 没有2-圈的有向图称为定向图．

引理1[2]设（X，Y）为定向图D中任意一个满足的弧割，则

定理1 设D是一个n阶强连通定向图，D的度序列为d1≥d2≥…dn．若λ＜δ，则λ

将X中的顶点按度的不增序进行排列，取前2δ+1个顶点组成的集合记为U.将Y中的顶点也按度的不增序排列，取前2δ+1个顶点组成的集合记为W.则有

即

引理2[2]设（X，Y ）是定向二部图D＝ （V ′∪ V″，A）中的任意一个满足的弧割，则，其中X′＝X∩V′，Y′＝Y∩V′，X″＝X∩V″，Y″＝Y∩V″．

定理2 设D＝ （V ′∪ V″，A ）是强连通定向二部图，D的度序列为d1≥d2≥…dn.若 λ＜δ，则

将X′中的顶点按度的不增序进行排列，取前δ+1个顶点组成的集合记为U′．将X″中的顶点按度的不增序排列，取前δ+1个顶点组成的集合记为U″．将Y′中的顶点按度的不增序排列，取前δ+1个顶点组成的集合记为W′．将Y″中的顶点按度的不增序排列，取前δ+1个顶点组成的集合记为W″．则有

引理3[3]若图G的团数 ω（G ）≤p，则2m（G

引理4 设D是一个团数ω（D）≤p的定向图，若D[X]是由D的顶点子集X导出的子图，则2m（ D [ X ]）

引理5[2]设定向图D的团数ω（D）≤p，则对D中任意一个满足的弧割（X，Y），有[X]

定理3 设D是一个团数ω（）D ≤p的n阶强连通定向图，D的度序列为d1≥d2≥…dn.记a＝max．若 λ＜δ，则

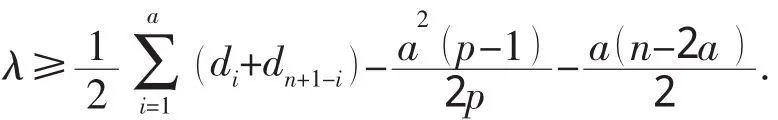
证明 设S是定向图D的最小弧割，则[S]＝λ.由弧割的定义知D-S至少包含两个强连通分支.设DS的强连通分支无圈序为D1，D2，…，Dk（ k≥2）.令X＝V（ Dk），Y＝V（D） V（ Dk），则（X，Y ）＝S．

因为 λ＜δ，所以由引理1可知[X ]≥2δ++1≥2δ-+1 故≥2δ+1.由引理

将X中的顶点按度的不增序进行排列，取前a个顶点组成的集合记为U.将Y中的顶点也按度的不增序排列，取前a个顶点组成的集合记为W．因为由引理4可得

所以

故

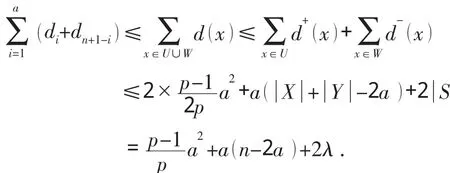
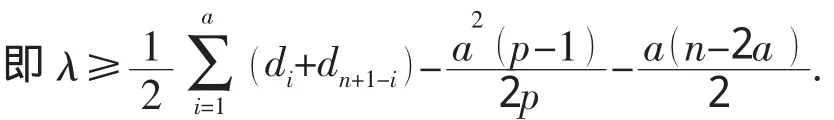
［1］Bang-Jensen JØ Jrgen，Gutin Gregory.Digraphs:theory,algorithmsand applications［M］.London：Springer-Verlag，2001.

［2］高敬振.有向图的边割（X，Y）中和的下界与有向图的极大性和超级性［J］.系统科学与数学，2011，12（5）：1603~1611.

［3］Turán P.An extremal problemin graph theory［J］.Matematikaiés Fizikai Lapok，1941，48：436~452.