两次求导圆梦参数分离法

含有自然对数函数的不等式恒成立，求参数取值范围问题，若用参数分离法将参数分离后，不等式的另外一边是一个超越函数，对该函数求导后往往仍然为一个超越函数，求其根常常难度很大.因此，命题人提供的参考答案通常是用分类讨论法来回避对超越函数的研究.而同学们往往不愿意分类讨论，却对参数分离法情有独钟，选择了参数分离法又因为超越函数难以处理而苦恼.实际上，实施参数分离后，对所得超越函数求导后的其中一部分函数，再求一次导数，问题常常可以解决，从而圆学生参数分离法之梦.

例 （北京市东城区2013—2014学年度一模（理科）（18）题）已知函数f（x）=ax2-4ln（x-1），a∈R.

（Ⅰ）当a=1时，求f（x）的单调区间;

（Ⅱ）已知点P（1，1）和函数f（x）图象上动点M（m，f（m）），对任意m∈[2，e+1]，直线PM倾斜角都是钝角，求a的取值范围.

1 参考答案给出的分类讨论法

解 （Ⅰ）当a=1时，f（x）=x2-4ln（x-1），定义域为（1，+∞），

f′（x）=2x-4x-1=2x2-2x-4x-1=

2（x+1）（x-2）x-1

所以当a=1时，f（x）的单调递增区间为（2，+∞），单调递减区间为（1，2）.

（Ⅱ）因为对任意m∈[2，e+1]，直线PM倾斜角都是钝角，

所以对任意m∈[2，e+1]，直线PM的斜率小于0，

即f（m）-1m-1<0，f（m）<1，

即f（x）在区间[2，e+1]上的最大值小于1.

令g（x）=ax2-ax-2

（1）当a=0时，f（x）=-4ln（x-1）在[2，e+1]上单调递减，

f（x）max=f（2）=0<1，显然成立，所以a=0.

（2）当a<0时，二次函数g（x）的图象开口向下，

且g（0）=-2，g（1）=-2，

x∈（1，+∞），g（x）<0，

故f′（x）<0，f（x）在（1，+∞）上单调递减，

故f（x）在[2，e+1]上单调递减，f（x）max=f（2）=4a<1，显然成立，所以a<0.

（3）当a>0时，二次函数g（x）的图象开口向上，

且g（0）=-2，g（1）=-2，

所以x0∈（1，+∞），g（x0）≤0.

当x∈（1，x0）时，g（x）<0，

当x∈（x0，+∞）时，g（x）>0.

所以f（x）在区间（1，+∞）内先递减再递增，

故f（x）在[2，e+1]上的最大值只能是f（2）或f（e+1）.

所以f（2）<1，

f（e+1）<1，即4a<1，

a（e+1）2-4<1，

所以0<a<14.综上a<14.

2 参数分离法

解法1 （Ⅰ）略.

（Ⅱ）因为对任意m∈[2，e+1]，直线PM倾斜角都是钝角，

所以对任意m∈[2，e+1]，直线PM的斜率小于0，

即f（m）-1m-1<0，f（m）<1，

又f（x）=ax2-4ln（x-1），

所以am2-4ln（m-1）<1对任意m∈[2，e+1]恒成立，

所以a<1+4ln（m-1）m2对任意m∈[2，e+1]恒成立.

设g（x）=1+4ln（x-1）x2（x>1），

则a小于g（x）在区间[2，e+1]上的最小值.

可求得g′（x）=2x3（x-1）[x-4（x-1）ln（x-1）+1]， ②

当x>1时，2x3（x-1）>0，则g′（x）的符号与x-4（x-1）ln（x-1）+1的符号一致.

令h（x）=x-4（x-1）ln（x-1）+1（x>1），

则h′（x）=-3-4ln（x-1）.

令h′（x）=0，则x=1+e-34，

令h′（x）>0，则1<x<1+e-34，

令h′（x）<0，则x>1+e-34.

故函数h（x）在（1，1+e-34）递增，在（1+e-34，+∞）递减，在x=1+e-34取最大值，即

h（x）max=h（1+e-34）=2+4e-34>0.

又h（2）=3>0，h（e+1）=2-3e<0，且函数h（x）图象在[2，e+1]连续不间断，

所以在[2，e+1]上存在x0，使得h（x0）=0.

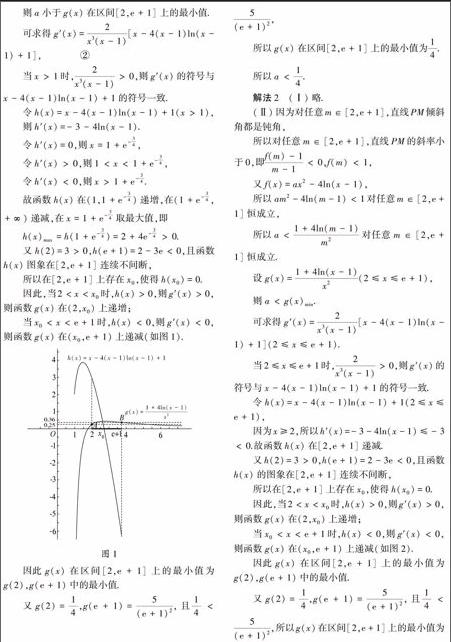
因此，当2<x<x0时，h（x）>0，则g′（x）>0，则函数g（x）在（2，x0）上递增;

当x0<x<e+1时，h（x）<0，则g′（x）<0，则函数g（x）在（x0，e+1）上递减（如图1）.

图1

因此g（x）在区间[2，e+1]上的最小值为g（2），g（e+1）中的最小值.

又g（2）=14，g（e+1）=5（e+1）2，且14<5（e+1）2，

所以g（x）在区间[2，e+1]上的最小值为14.

所以a<14.

解法2 （Ⅰ）略.

（Ⅱ）因为对任意m∈[2，e+1]，直线PM倾斜角都是钝角，

所以对任意m∈[2，e+1]，直线PM的斜率小于0，

即f（m）-1m-1<0，f（m）<1，

又f（x）=ax2-4ln（x-1），

所以am2-4ln（m-1）<1对任意m∈[2，e+1]恒成立，

所以a<1+4ln（m-1）m2对任意m∈[2，e+1]恒成立.

设g（x）=1+4ln（x-1）x2（2≤x≤e+1），

则a<g（x）min.

可求得g′（x）=2x3（x-1）[x-4（x-1）ln（x-1）+1]（2≤x≤e+1）.

当2≤x≤e+1时，2x3（x-1）>0，则g′（x）的符号与x-4（x-1）ln（x-1）+1的符号一致.

令h（x）=x-4（x-1）ln（x-1）+1（2≤x≤e+1），

因为x≥2，所以h′（x）=-3-4ln（x-1）≤-3<0.

故函数h（x）在[2，e+1]递减.

又h（2）=3>0，h（e+1）=2-3e<0，且函数h（x）的图象在[2，e+1]连续不间断，

所以在[2，e+1]上存在x0，使得h（x0）=0.

因此，当2<x<x0时，h（x）>0，则g′（x）>0，则函数g（x）在（2，x0）上递增;

当x0<x<e+1时，h（x）<0，则g′（x）<0，则函数g（x）在（x0，e+1）上递减（如图2）.

因此g（x）在区间[2，e+1]上的最小值为g（2），g（e+1）中的最小值.

又g（2）=14，g（e+1）=5（e+1）2，且14<5（e+1）2，

所以g（x）在区间[2，e+1]上的最小值为14.

所以a<14.

图2

解法3 （Ⅰ）略.

（Ⅱ）因为对任意m∈[2，e+1]，直线PM倾斜角都是钝角，

所以对任意m∈[2，e+1]，直线PM的斜率小于0，

即f（m）-1m-1<0，f（m）<1，

又f（x）=ax2-4ln（x-1），

所以am2-4ln（m-1）<1对任意m∈[2，e+1]恒成立，

所以a<1+4ln（m-1）m2对任意m∈[2，e+1]恒成立.

设g（x）=1+4ln（x-1）x2（2≤x≤e+1），

则a<g（x）min.

可求得g′（x）=2x3[1+2x-1-4ln（x-1）].

当2≤x≤e+1时，2x3>0，则g′（x）的符号与1+2x-1-4ln（x-1）的符号一致.

令h（x）=1+2x-1-4ln（x-1）（2≤x≤e+1），

易观察出函数h（x）在[2，e+1]递减.

又h（2）=3>0，h（e+1）=-3+2e<0，且函数h（x）图象在[2，e+1]连续不间断，

所以在[2，e+1]上存在x0，使得h（x0）=0.

因此，当2<x<x0时，h（x）>0，则g′（x）>0，则函数g（x）在（2，x0）上递增;

当x0<x<e+1时，h（x）<0，则g′（x）<0，则函数g（x）在（x0，e+1）上递减（如图3）.

因此g（x）在区间[2，e+1]上的最小值为g（2），g（e+1）中的最小值.

又g（2）=14，g（e+1）=5（e+1）2，且14<5（e+1）2，所以g（x）在区间[2，e+1]上的最小值为14.所以a<14.

图33 两类解法的比较

参考答案给出的①式f′（x）=2（ax2-ax-2）x-1的分子不再含有自然对数，但需要关于a分类讨论.

本文给出的解法1实施参数分离后得到a<1+4ln（m-1）m2，设g（x）=1+4ln（x-1）x2（x>1），对其求导后得到的②式g′（x）=2x3（x-1）[x-4（x-1）ln（x-1）+1]中的“x-4（x-1）ln（x-1）+1”部分仍然含有ln（x-1），又很难求其根，解题到此往往搁浅.而事实上只要对函数h（x）=x-4（x-1）ln（x-1）+1再求一次导数后，便可以见到胜利的曙光了.

本文给出的解法2注意到函数1+4ln（x-1）x2是一个确定的函数，因此只须研究它在题目给定区间[2，e+1]上的情况即可，因此引入的新函数为g（x）=1+4ln（x-1）x2（2≤x≤e+1），引入的另外一个新函数为h（x）=x-4（x-1）ln（x-1）+1（2≤x≤e+1），解题长度比方法1要短.

本文给出的解法3选择研究的函数h（x）=1+2x-1-4ln（x-1）（2≤x≤e+1）甚至不求导也能够判断出h（x）的单调性，可以使参数分离法更容易完成.

作者简介 李春雷，男，1967年10月生，河北香河人，中学高级教师，北京市骨干教师，全国初等数学研究会第二届、第三届理事会常务理事，北京师范大学研究生院2013级在读教育博士.主要研究高中数学教师教育创新途径、中学数学教育理论、解题教学、高考命题等.

曾获首届丘成桐中学数学奖、全国“紫金杯”数学创新奖、全国初等数学青年研究奖、北京市第三届基础教育教学成果奖、全国教师教育学会综合实践活动先进个人等荣誉称号，在省级、国家级刊物上公开发表数学论文100余篇，多篇文章被中国人民大学报刊资料复印中心全文转载.