关于积分型Cauchy中值定理的一个结论

李冬辉

(河南教育学院 数学与统计学院，河南 郑州 450046)

关于积分型Cauchy中值定理的一个结论

李冬辉

(河南教育学院 数学与统计学院，河南 郑州 450046)

研究当积分区间长度趋于无穷时，积分型Cauchy中值定理中间点的渐近性质，同时得到Lagrange中值定理中间点的渐近性质.

积分型Cauchy中值定理；Lagrange中值定理；中间点；渐近性

0 引言

当区间长度趋于零时，对于中值定理中间点的渐近性质，有学者进行了研究并得出了一些有意义的结论[1-4].文献[1]和文献[2]研究了在积分区间长度趋零时，积分型Cauchy中值定理中间点的渐近性.本文用另一种方法讨论当积分区间长度趋于无穷时，积分型Cauchy中值定理中间点的渐近性质，在弱于文献[1]定理3的条件下，得出了具有一般形式的结果.作为此结果的一个特例，又得出当区间长度趋于无穷时，Lagrange中值定理中间点渐近性具有的一般形式的结果.

首先引述积分型Cauchy中值定理和Lagrange中值定理.

积分型Cauchy中值定理 若①f(t),g(t)在[a,x]上连续；②g(t)≠0,t∈[a,x]，则在(a,x)内至少存在一点ξ,使得

(1)

其中ξ称为积分型Cauchy中值定理的中间点.

Lagrange中值定理 设函数F(t)在[a,x]上连续，在(a,x)内可导，则在(a,x)内至少存在一点ξ,使得

F(x)-F(a)=F′(ξ)·(x-a)，

(2)

其中ξ称为Lagrange中值定理的中间点.

1 主要定理

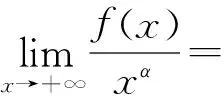
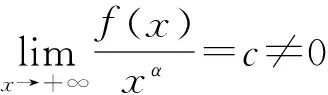
进而有

所以

(3)

同理

(4)

由(1)，(3)，(4)式得

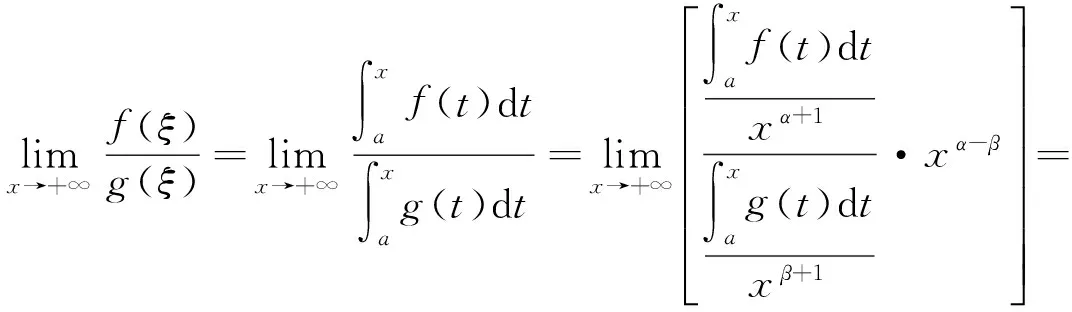
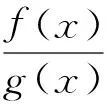
一方面，由(3)，(4)式得

(5)

另一方面，由(1)式得

由定理1条件及L’Hospital法则，得

(6)

从而，由(5)，(6)式得

即有

所以

推论1 设F′(x)在[a,+∞)内连续，若存在α>0，使

则对于Lagrange中值定理确定的中间点ξ，有

(7)

证明在(1)式中，取f(t)=F′(t),g(t)=1，得

即

F(x)-F(a)=F′(ξ)·(x-a).

从而，(1)式中的积分型Cauchy中值定理确定的中间点ξ，即为(2)式中的Lagrange中值定理确定的中间点ξ.再取β=0，根据推论的条件，由定理1知(7)式成立.

[1] 刘文武，严忠权．积分型Cauchy中值定理中间点的渐近性[J]．数学的实践与认识，2010，40(11)：228-231．

[2] 戴立辉，刘龙章．积分型Cauchy中值定理中间点的渐近性[J]．大学数学，2009，25(3)：168-172.

[3] 高国成.微分中值定理“中间点”的渐近性[J].工科数学，2001,17(5):102-104.

[4] 张广梵.关于微分中值定理的一个注记[J].数学的实践与认识，1988，18(1)：87-89.

A Conclusion on Integral Type of Cauchy Mean Value Theorem

LI Dong-hui

(SchoolofMathematicsandStatistics,HenanInstituteofEducation,Zhengzhou450046,China)

The asymptotic properties for median point of integral Cauchy mean-value theorem with infinite integration interval were studied, and a conclusion about the asymptotic property for median point of Lagrange mean-value theorem is given.

integral Cauchy mean-value theorem; Lagrange mean-value theorem; median point; asymptotic property

2014-09-28

河南省教育厅科学技术研究重点项目(13A140224)

李冬辉(1963—)，男，河南许昌人，河南教育学院数学与统计学院副教授，主要研究方向：基础数学.

10.3969/j.issn.1007-0834.2015.01.006

O172.2

1007-0834(2015)01-0018-03