立体几何四解套
2015-03-26胡建军
胡建军


数学教学很大程度上归结为数学解题,立体几何特别利用几何法对于训练学生的空间位置和数量关系的,在初中平面几何的基础上有了更高的思维。所谓几何法:就是从条件出发,以定义、公理、定理为依据,通过辅助构图和推理,计算解决。它需要一定的空间想象力和逻辑思维能力。当然平面几何的知识是离不开的基础。说是立体几何,研究是空间的,但始终要转化为平面的。能否添加合适的辅助线和进行有效的转化是解决该题的关键。
如何有效、高效地突破和搞定立几这个高考必考的大题?当然一方面需要学生能对这个空间几何体的直观认识看到位,另一方面笔者从大量的题解中总结出以下四点经验。相信对读者解决立体几何的困惑受益匪浅。
一、立体几何的解题策略
1.底面平面化(研究的图形,如三角形、四边形,拎出来平面化)
根据立体图形的直观图斜二测画法,水平放置的平面图形跟实际有较大差异,要认识几何体,首先要认清底面的平面图,所以在认识该几何体之前,先画出底面的原形(底面俯视图),在有关数量(长度)和位置(角度)的计算时亦如此,否则很多时候学生会看“走眼”。
例1.如图1,PO⊥平行四边形ABCD,AC,BD交于点O,∠ADC=45°,AD=AC=1,PO=2,M为PD的中点。
(1)求MA与面ABCD所成角的正切值;
(2)求二面角P-AD-C的平面角的余弦值。
2.有中点用好中位线、有等腰三角形用好三线合一
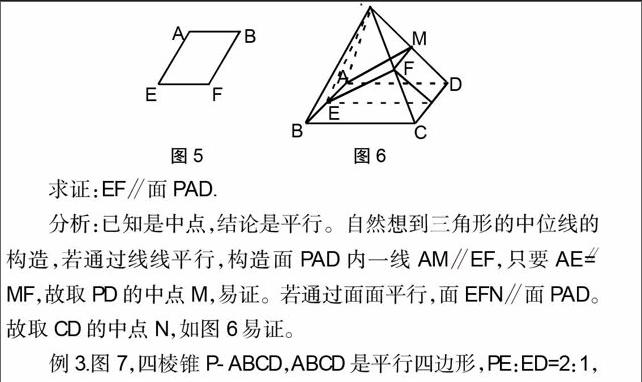
例3.图7,四棱锥P-ABCD,ABCD是平行四边形,PE:ED=2:1,在棱PC上确定一点F,使得BF∥面AEC。
分析:我们常用线线平行来判定线面平行,怎样在面ACE内找一条与BF平行?若过BF的面交面ACE与OM(图7),则应有OM∥BF,由三角形的中位线知M为DF的中点,由策略1把研究的平面PCD拎出来(图8),由平面几何及三角形中位线不难可得F为PC的中点;当然我们也常用面面平行得到线面平行,若过BF的面BFN∥面ACE,则应有BN∥OE,FN∥CE同样可得F为PC的中点。
点评:立体几何中的研究关系,归根结底转化为线线关系,而在有关平行的问题当中,充分利用三角形的中位线及平行线分线段成比例,往往可使有关图形一线牵。
3.若有面面垂直,务必作出线面垂直
立体几何中最重要的位置关系是线面垂直,可以说无(垂)线不成题,几何体中必定会有面的垂线,或已知、或隐藏、或推证、或求作。而面面垂直的性质定理:若两面垂直,则在一个平面内垂直于交线的直线垂直于另外一个平面。给了我们如何显现面的垂线的一个方法!若两相交平面垂直于第三个平面,求证两相交平面的交线垂直于第三个平面。必须把面面垂直转化为线面垂直(在证明时在一面内作交线的垂线),从而通过线线之间的垂直关系解决相关问题。
例4.见例2,如图3,(2)求PB和面PAC所成的角的余弦值;(3)求二面角A-PD-C的平面角的余弦值。
(1)求证:PC⊥面BDE;
(2)若A-PB-C为90°,求PD与面PBC所成的角。
分析:(1)由策略1拎出来△PAC,(图11)平面几何知识可得OE⊥PC,而BD⊥面PAC,∴PC⊥BD,∴PC⊥面BDE。
点评:存在面面垂直,点向面作垂线转化为点向两面的交线作垂线,原则上必须给出。
4.问题总是空间的、研究总是平面的
(1)求异面直线PD与BC所成角的余弦值;
(2)求二面角P-AB-C的大小;
点评:通过庖丁解牛,把平面图看透,把空间中的问题转化为相应的平面中去,而后无非是初中的三角形或四边形的平面几何知识或解三角形等问题。
二、用好四解套,考题做着笑
(1)求证:MN∥面ABCD;
(2)过点A作AQ⊥PC于Q,求二面角A-MN-Q的平面角的余弦值。
(1)求证:PQ∥BCD;
(2)若二面角C-BM-D的大小为60°,求C-BM-D的大小。
分析:(1)利用线线平行证线面平行,如图利用中位线等易证 为平行四边形;(2)由垂线法求作C-BM-D的二面角,作CO⊥BD,OH⊥BM,连接CH,则∠BDC=60°就是C-BM-D的二面角;
(1)求证:DE⊥面ACD;
(2)求二面角B-AD-E的大小.
(2)由垂线法,由B向面ADE作垂线,直观感知,垂足落在 外面了,但垂足一定在某条特定的线上,图24把该几何体“补完整”(把△ACD平移至外面),则作BO⊥A1E,OH⊥AD,连接BH,θ=∠BHO是二面角B-AD-E的平面角,由图26及解套4不难求得θ=∠BHO=30°.
三、一点感悟
数学教育家波利亚说过,掌握数学就意味着要善于解题。当我们碰到一个新的内容时,总想到用熟悉的题型、知识点去“套”,这应该是基于解出来的基本要求,也正是基于这基本的要求,才能提出新看法,不断利用旧有的东西解决新问题。充分利用数学学科的逻辑思维优势,让学生在解决问题中逐步体会某一数学内容的思维方式,慢慢揭开学科内容的本质,挖掘这一内容蕴含的思想价值和处理方式,真正关注对问题本质的透视,希望这样的教育教学研究能成为师生数学学习的一种常态。
编辑 薛直艳
