复合高斯杂波下的3种目标检测算法研究*

付克兰,詹 旭

(1.成都农业科技职业学院 信息技术分院，四川 成都 611130；2.四川理工学院，四川 自贡 643000)

复合高斯杂波下的3种目标检测算法研究*

付克兰1,詹 旭2

(1.成都农业科技职业学院 信息技术分院，四川 成都 611130；2.四川理工学院，四川 自贡 643000)

针对复合高斯分布背景下的慢速目标检测问题，从贝叶斯统计检测理论出发，系统分析了最优的GLRT检测算法、次优的基于AR模型的目标检测算法和传统的自适应MTI检测算法。结合这3种算法的特点阐述了它们的检测性能和工程可实现性。并在最后通过IPIX雷达实测海杂波数据对上述结论进行了验证，实验结果表明在性能损失不大时，基于AR模型的目标检测算法易于工程实现。

GLTR；AR模型；自适应MTI；MTD

0 引 言

在海杂波背景下检测微弱慢速目标是目前大部分舰载或岸基雷达所面临的急需解决的重大问题。而其中的关键技术是对复杂海杂波背景的抑制。由于海面环境比较复杂，海杂波受浪高、风速、持续时间、极化、波束入射角、频率等参数的影响，海杂波模型不再服从经典的瑞利分布，因此基于瑞利分布的经典海杂波背景下的目标检测方法很难处理这种情况。大量的研究结果表明复合高斯分布能较好地描述海杂波统计模型[1-2]。本文就复合高斯分布的海杂波背景下的目标检测问题，从经典的贝叶斯检测理论[3]出发，即理论推导该理论下最优的GLRT检测算法[3-9]。该检测性能最优，但需要大量参考数据估计杂波协方差矩阵，而且计算量较大，很难工程实现。在此基础上分析最优GLRT检测器的一种低阶近似实现方法—基于AR(自回归)模型的检测技术[10-13]。这种方法只需要少数参考信号，且计算量大幅减小，且能较好地模拟低阶复合高斯杂波。同时我们还介绍了MTI(运动目标显示)级联MTD(运动目标检测)常用的目标检测算法[14-15]。

本研究从经典的广义似然比检测理论出发，给出了理论上最优的海杂波背景下的目标检测算法，并分析了实现该方法的关键是海杂波协方差矩阵和目标多普勒频率的估计；同时，在分析了AR模型与海杂波谱的特点后，给出了基于AR模型的海杂波抑制级联目标检测算法；然后，自适应的MTI海杂波抑制算法也被应用到海杂波的抑制中，将抑制杂波后的回波做MTD处理实现目标能量的积累。另外，结合上述各种算法的特点以及雷达可能面临着的问题，给出各种算法的具体实现步骤。最后，为了对上述算法进行性能验证和横向性能比较，本研究还分别给出了加拿大IPIX雷达海杂波实测数据和仿真数据下这几种算法的目标检测结果。

1 回波模型

假设待检测单元回波数据是传感器接收的N个相干回波采样，并且表示为：z=[z(0),z(1),…,z(N-1)]T。则二元假设检验可以表示成：

(1)

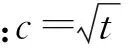
根据贝叶斯检测理论的奈曼-皮尔逊准则[9]，最优检测器是似然比检测统计量。但是由于复合高斯杂波统计分布复杂，不能得到假设模型下的最优检测器LRT形式。因此，有必要对回波模型(1)下的各种次优检测器进行研究。

2 海杂波背景下的目标检测算法研究

2.1 基于广义似然比检测(GLRT)的检测算法

假设将回波杂波中的纹理τ建模成一确定的未知参量，可以根据广义似然比检测(GLRT)理论，推导基于GLRT的检测统计量[3-7]

(2)

式中，p为目标驱动向量，z为待检测距离单元的回波数据，N是z的样本个数，M为海杂波协方差矩阵。要实现式(2)表示的最优检测器，需要解决两个关键的技术：协方差矩阵M的估计，目标驱动向量p的确定。

海杂波协方差矩阵的估计通常是利用辅助海杂波数据来获得的。辅助海杂波数据是指与待检测距离单元数据服从相同分布的时间或空间上相邻距离单元的海杂波数据。利用这些辅助数据，我们可以采用归一化的样本协方差矩阵估计算法：

其中，zt为第t个距离单元的回波数据，N是zt的样本个数，K为距离单元个数(K≥2N)。值得注意的是，为了估计的协方差矩阵在式(1)中求逆时不奇异，辅助数据要足够多，即K需要满足。

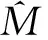
(3)

该算法的具体步骤为：

2)按式(3)对回波进行杂波抑制；

3)对抑制后的回波进行脉间积累(FFT变换)；

4)距离维CFAR。

2.2 基于AR模型的检测算法

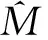
其具体步骤：

(1)利用静态杂波估计杂波AR模型阶数；

(2)利用时间和空间临近杂波回波估计杂波AR模型系数；

(3)对回波进行基于AR模型的海杂波抑制算法；

(4)对滤波后回波脉间FFT实现相干积累；

(5)对处理后的数据进行距离维的CFAR并判决结果输出。

该算法的特点是算法简单，易于实现，对辅助数据的数量要求也相对较低，在海杂波阶数较低时还能获得趋近最优检测算法的性能；但是当海杂波AR模型阶数较大时，对海杂波模型的估计不够准确，性能损失较大。此时需要实时估计AR模型阶数，并且阶数增大后该算法的计算量也会相应增大。

2.3 自适应MTI+MTD

海杂波谱通常不在零频，需要估计杂波谱中心，再对谱中心补偿，然后进行杂波抑制，这种方法称为运动杂波谱中心补偿抑制法[10]。对抑制后的滤波数据进行脉间积累及距离维CFAR。但是，当目标刚好落在海杂波谱区间时，这种方法会造成目标丢失。其算法流程如图2所示。

该算法的具体步骤为：

(1)估计杂波中心谱fd；

(2)中心频率为fd的MTI操作；

(3)对MTI操作后的回波进行脉间相干积累，再作CFAR检测。

该算法的特点是传统操作，易于实现，但是当目标多普勒与海杂波谱中心相同或相邻时，会丢失目标。此时需要参数化的海杂波估计方法才能有效地区分目标与杂波的特点，即基于GLR的估计方法及其低阶近似—基于AR模型的估计算法。

3 数值结果

数值结果分实测数据和仿真数据两部分进行，其中实测数据主要验证上述算法的海杂波抑制性能，而检测性能是通过MonteCarlo实验获得的，受限于实测数据的样本个数，我们借助于仿真数据获取上述算法的检测性能。

所用的实测海杂波数据为IPIX雷达的1993年采集数据。IPIX雷达的系统参数：雷达工作频率：9.39 GHz；脉冲宽度：200 ns；脉冲重复频率：1 000 Hz。

最大不模糊速度：7.987 2 m/s；波束宽度：0.9°；天线增益：45.7 dB；PRF样本个数：6 000；距离单元：14。仿真数据是由MATLAB随机产生服从K分布的海杂波数据

仿真结果分3个部分：海杂波功率谱与AR模型的拟合、海杂波抑制结果、及海杂波背景下的目标检测结果。需要说明的是：前两部分所用数据为一个距离单元的4 000个样本的慢时间历程。另外，由于基于GLRT检测算法中协方差矩阵的维数与脉冲个数相同，难以实现全慢时间历程的所有样本的杂波抑制，因此在实测数据数值结果部分没有给出这种方法的杂波抑制结果。

3.1 IPIX海杂波功率谱与AR模型的拟合情况

图3是IPIX雷达实测海杂波的功率谱与3阶、6阶和12阶AR模型的对比。

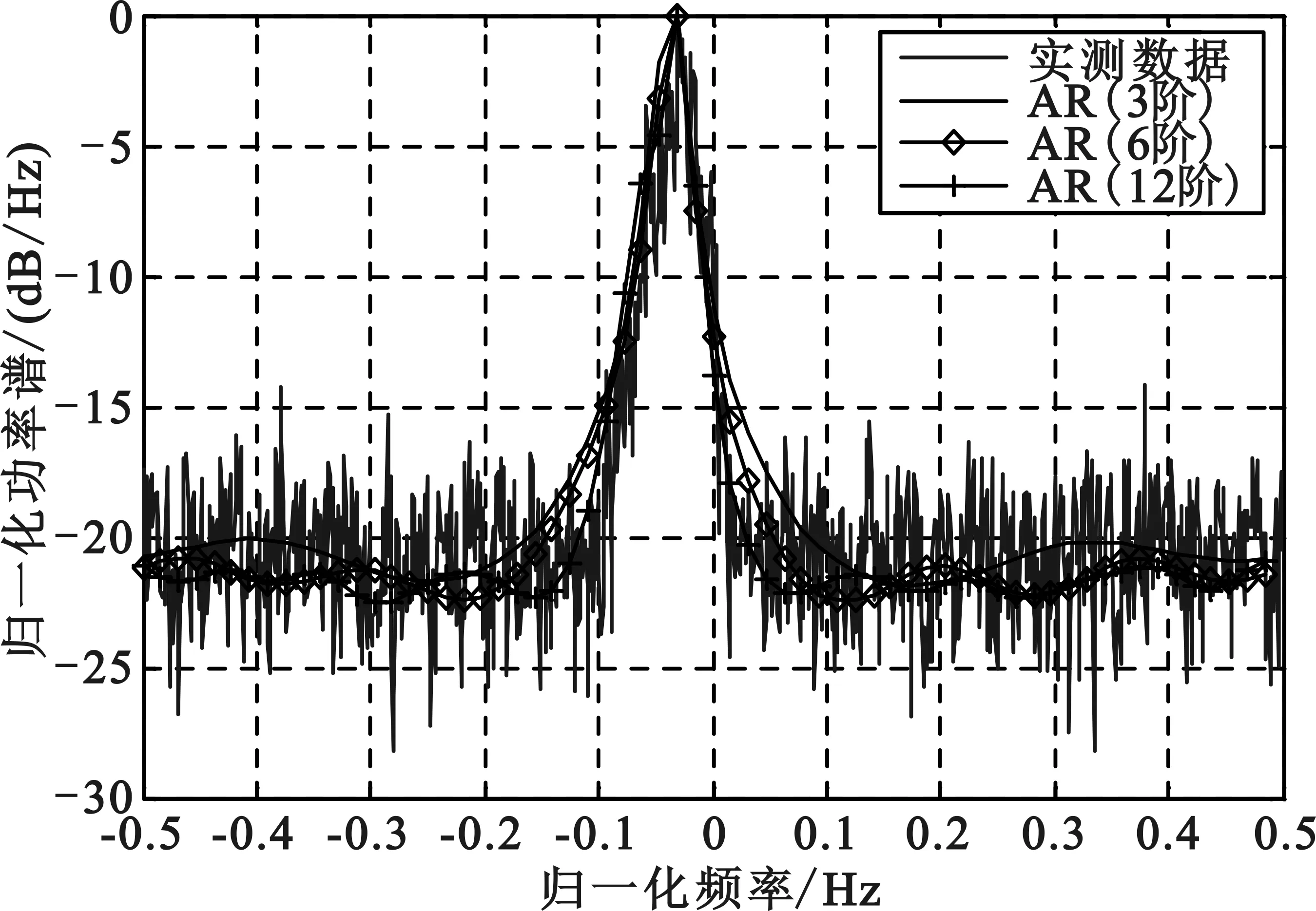
图3 海杂波功率谱与AR模型的拟合情况

从图3可以看出，AR模型能较好的拟合实际海杂波功率谱。上述3种不同阶数的AR模型都能较好的拟合海杂波。并且阶数越大，在过渡带等细节部分拟合效果更好。不过随着阶数增大，计算量会变大。在实际工程中，需要根据具体情况折中考虑。

3.2 IPIX海杂波的抑情况制

在这一部分的数值结果中，我们选择AR模型的阶数为6。对IPIX海杂波进行AR模型杂波抑制和自适应MTI(图4选取的阶数为3阶)的结果如图4所示。

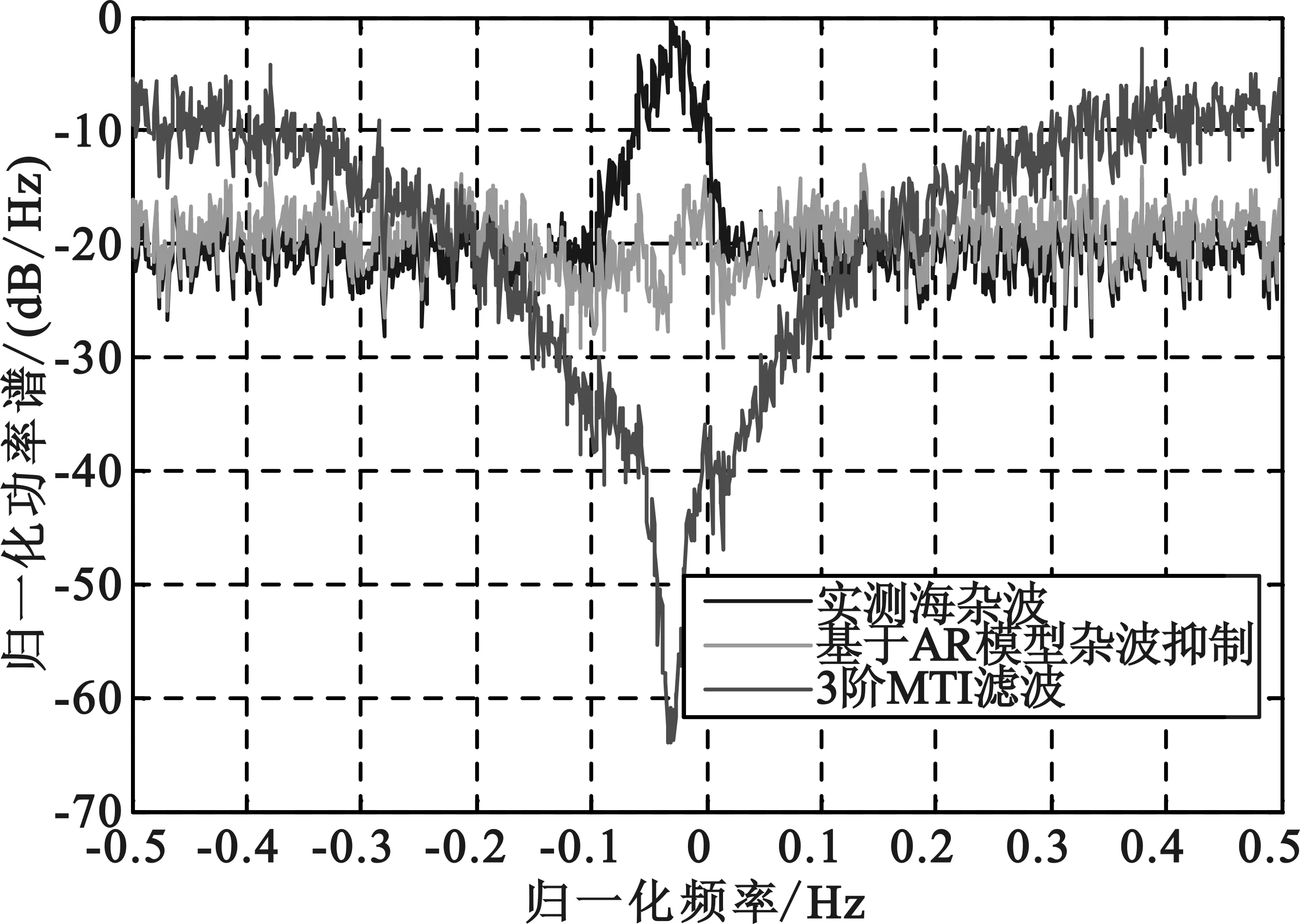
图4 海杂波抑制输出

图4是海杂波源功率谱、基于AR模型的海杂波抑制后结果和3阶MTI滤波输出。可以看出AR模型能很好的将海杂波白化，便于后面的检测。而自适应3阶MTI滤波能在海杂波多普勒频带内较好的抑制海杂波。

图5所出来的回波为IPIX雷达所测海杂波中加目标信号。由于通过估计得海杂波的运动谱中心为30 Hz，我们将目标多普勒也设定为30 Hz。

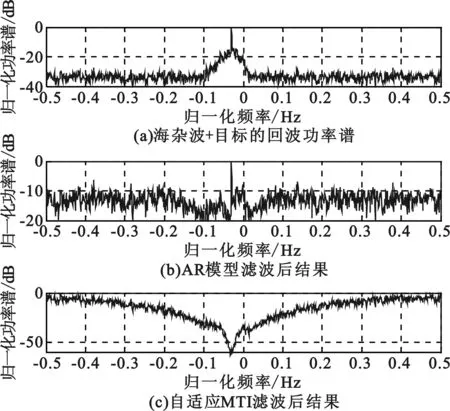
图5 海杂波+目标信号后的海杂波抑制结果对比

图5的处理结果可以看出，由于目标刚好落在了海杂波的频带内，常规的MTI将目标当成杂波滤除掉了(如图5(c)所示)。而基于AR模型的海杂波抑制算法却能在抑制海杂波的同时保留目标信息(如图5(b)所示)。这是因为AR模型的滤波器学习了海杂波的相关性，能对海杂波进行针对性的抑制，而MTI滤波器只是对频带窗内的信号进行抑制，但对目标和杂波不具备选择性，在抑制杂波的同时将落入频带内的目标也滤掉了。当然，如果目标信号不在海杂波的频带内，自适应MTI滤波器也能取得较好的目标检测结果。

由图5的结果表明，自适应MTI+MTD目标检测算法适用于信噪比较高的情况下，并且最好是具有一定的目标多普勒的信息，当目标多普勒落在海杂波谱区间时，直接进行MTD；当目标多普勒频率落在非杂波区时就可以利用上述的自适应MTI+MTD。

3.3 海杂波背景下的目标检测技术性能

在这一部分，我们采用k分布的仿真数据，k分布表达式为：

(4)

式中，Γ(·)是伽马(gamma)函数，Kv-1(·)是(v-1)阶第二类修正的贝塞尔(Bessel)函数。v和u分别是K分布的形状参数和尺度参数，v越小表示杂波越尖锐。在下面仿真结果中，我们分别设杂波的形状参数v=1.5和尺度参数u=1，而杂波的脉间相关性是按照IPIX雷达实测数据估计值设定的。

仿真结果分两部分，分别给出设定信杂比(SCR)下目标多普勒频率在海杂波谱区间和非海杂波谱区间时，3种算法的距离维检测统计量曲线。其中，SCR定义为：

SCR=|α|2pHM-1p

1)当目标多普勒频率在海杂波谱区间时

在图6中选用的参数分别为：目标多普勒频率为-28 Hz，目标在第100个距离单元，AR模型阶数为4，SCR为32 dB。图6中的检测结果表明，基于GLRT的检测算法性能最优，基于AR模型的杂波抑制+MTD检测算法要优于直接MTD的检测结果。图中线1表明：由于目标多普勒在海杂波谱区间内，目标被强杂波淹没，而在其他距离单元出现了虚假目标。

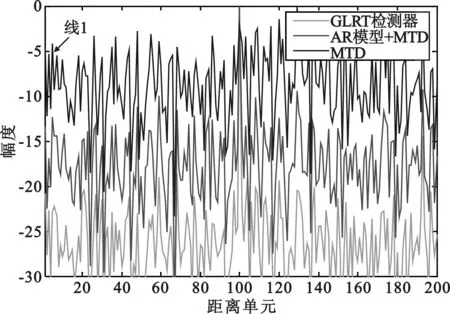
图6 门限检测基于GLRT,基于AR模型和

2)当目标多普勒频率不在海杂波谱区间时

图7中将目标多普勒设为-200 dB， MTI是中心频率为-30 Hz的两脉冲对消，其它参数与图6相同。

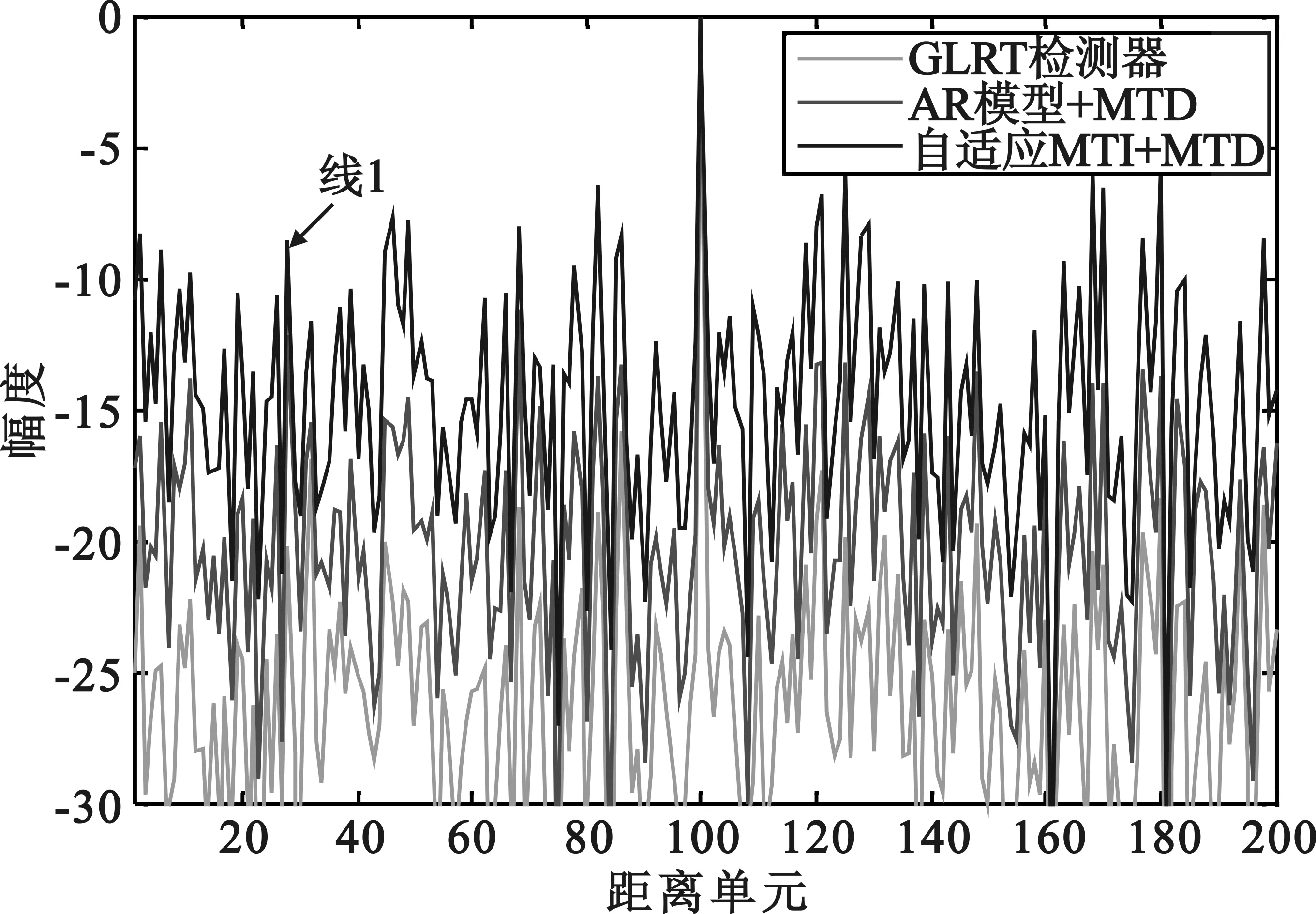
图7 门限检测基于GLRT,基于AR和

图7的结果显示基于GLRT和AR模型的检测器性能与图6中的相同，只是AMTI+MTD的检测算法性能得到了改善，线1表明该方法能正确地发现目标了。

4 结 语

本文主要针对强海杂波背景下的弱目标检测问题，系统地分析了3种不同海杂波抑制及目标检测算法。基于海杂波服从复合高斯模型以及经典的统计理论，推导了海杂波背景下GLRT检测器，给出其算法的理论推导、具体实现步骤、算法性能及其特点；然后我们根据AR模型理论提出了基于AR模型的海杂波抑制算法，并给出了该算法的基本思想及其结合MTD实现目标检测的具体步骤；同时，我们也给出了传统的自适应MTI级联MTD的实现方法。

本文还结合IPIX雷达实测海杂波数据对上述3种算法的特点及性能进行了进一步的验证和比较。综合上述3种海杂波抑制及目标检测算法的特点及仿真结果，我们给出以下结论：

(1)基于GLRT的检测器具有最好的检测性能，但是该方法需要足够多的辅助数据，并且计算量最大；

(2)基于自适应MTI级联FFT脉间相干积累的算法最简单，并且最易于实现，但是对信杂比的需求较高，并且容易丢失目标多普勒与海杂波频谱相近的目标；

(3)基于AR模型杂波抑制技术结合FFT的脉间相干积累算法其性能和计算量都介于两种方法之间。在大部分海情下能较好地描述海杂波特性，易于工程实现。

如何进一步提高复杂海杂波背景下的低速目标检测性能，并且具有高可工程实现性的检测算法将是我们接下来的研究内容。

[1] 姜斌.地、海杂波建模及目标检测技术研究[D],博士毕业论文.国防科技大学 .2006. JIANG Bing. Earth, the Sea Clutter Modeling and Target Detection Technology Research[D]. National University of Defense Technology Doctoral Dissertation. 2006.

[2] Conte E,Maio A D,Ricci G. Covariance Matrix Estimation for Adaptive CFAR Detection in Compound-Gaussian Clutter. IEEE Trans. on Aeros. and Electr. Syst[J] 2002, 38(2): 415-426.

[3] Kay S M. Fundamentals of Statistical Signal Processing, Volume I, Estimation Theory; VolumeⅡ[D], Detection Theory. Electronic Industry Press,2006.

[4] LI Na, CUI Guo-long, et al. Knowledge-Aided Bayesian Detection for MIMO Radar in Compound-Gaussian Clutter with Inverse Gamma Texture[J]. 2015 IEEE Radar Conference, 2015: 0777-0782.

[5] Sangston K J, et al. Adaptive Detection of Radar Targets in Compound-Gaussian Clutter[J]. 2015 IEEE Radar Conference, 2015: 0587-0592.

[6] Breloy A,Ginolhac G, et al. CFAR Property and Robustness of the Lowrank Adaptive Normalized Matched Filters Detectors in Low Rank Compound Gaussian Context[J]. 2014 IEEE 8thSensor Array and Multichannel Signal Processing Workshop (SAM). 2014: 301-304.

[7] Gini F. Performance Analysis of Two Structured Covariance Matrix Estimators in Compound-Gaussian Clutter[J]. Sign. Process. 2000, 80(2): 365-371.

[8] 邹鲲，廖桂生，等. 复合高斯杂波下的距离扩展目标的自适应检测[J].电子与信息学报,2013(07):1555-1561. ZOU Kun, LIAO Gui-sheng. Distance Extension Targets under the Complex Gaussian Clutter Adaptive Detection [J].Journal of Electronics and Information. 2013(07): 1555-1561.

[9] 简涛，苏峰，等. 基于bayes框架的复合高斯杂波下的稳健检测[J].电子学报, 2012(05): 990-994. JIAN Tao, SU Feng, et al. Robust Detection under the Compound Gaussian Clutter based on the Bayes Frame[J]. Electronic Journals, 2012(05): 990-994.

[10] SHUAI X,KONG L and YANG J, Improved AR-based GLRT Detector for Range-Spread Targets in Compound-Gaussian Clutter Without Secondary Data[J], Journal of Electronic Science and Techonology, 2010,9(2):16-23.

[11] SHUAI X, KONG L and YANG J. AR-Mode-based Adaptive Detection of Range-Spread Targets in Compound Gaussian Clutter[J], Signal Processing, 2011.91: 750-758.

[12] Alfano G, Maio A D, Farina A. Model-based Adaptive Detection of Range-Spread Targets[J]. IEE Proc.-Radar Sonar and Navig, 2004, 151(1): 2-10.

[13] Sheikhi A, Nayebi M M, Aref M R. Adaptive Detection Algorithm for Radar Signals in Autoregressive Interference[J]. IEE Proc.-Radar, Sonar Navig., 1998, 145(5): 309-314.

[14] 丁鹭飞，耿富录.雷达原理[D].西安电子科技大学出版社，2002. DING Lu-fei, GENG Fu-lu. Principles of Radar[D]. Xi’an University of Electronic Science and Technology Press,2002.

[15] 尹成斌，陈希信. MTI级联MTD的信噪比增益[J].现代雷达, 2012(05): 23-25. YIN Cheng-bing, CHEN Xi-xin. SNR Gain of Radar Signal by MTI and MTD [J]. Modern Radar, 2012 (05) : 23 -25.

付克兰 (1972—),女,硕士,讲师,主要研究方向为电子信息，图像处理；

詹 旭(1981—)，女，硕士，讲师，主要研究方向为信号与信息处理，图像处理。

Three Target Detection Algorithms in Compound-Gaussian Clutter

FU Ke-lan1,ZHAN Xu2

(1.Information Technology School, Chengdu Vocational College of Agricultural Science and Technology, Chengdu Sichuan 611130,China;2.Sichuan University of Science & Engineering, Zigong Sichuan 643000, China)

Aiming at the low-speed target detection problem in compound Gaussian clutter, and based on the theory of Bayes statistic detection, three detection algorithms are systematically analyzed,including optimal GLRT (Generalized Likelihood Ratio Test) detection algorithm, suboptimal AR-based target detection algorithm, and traditional adaptive MTI (Moving Target Indicator) detection algorithm. Detection performance and engineering implementation are described in combination with the characteristics of the mentioned three methods. Finally, the above conclusion is verified by the sea clutter data of IPIX radar actual measurement. Experimental results show that the AR -based target detection algorithm is easy for engineering implementation when the performance loss is under control.

GLTR；AR model；adaptive MTI；MTD

10.3969/j.issn.1002-0802.2015.11.009

2015-06-18；

2015-10-09 Received date:2015-06-18；Revised date：2015-10-09

TN958.6

A

1002-0802(2015)11-1251-06