一移相H桥变换器的一种新型软开关拓扑

张加胜, 徐向华, 陈 荣, 郝秀杰

(中国石油大学信息与控制工程学院,山东青岛 266580)

一移相H桥变换器的一种新型软开关拓扑

张加胜, 徐向华, 陈 荣, 郝秀杰

(中国石油大学信息与控制工程学院,山东青岛 266580)

针对目前软开关变换器拓扑结构复杂、损耗较大的问题,提出移相H桥变换器的一种新型软开关拓扑,基于原有的逆变变压器和整流、滤波元件,增设一种无源辅助箝位电路,拓扑结构简单易行,无需有源器件和附加控制,通过其换流重叠及续流、箝位作用,实现超前桥臂的零电压通断和滞后桥臂的零电流通断,有效地降低变换器损耗和提高系统效率。对新型软开关拓扑进行原理定性阐述,结合各时段波形进行理论分析,得出有关软开关条件。实验结果证实了本拓扑方案及理论分析方法的有效性。

移相H桥; 拓扑; 软开关; 无源辅助箝位

近年来,有关移相H桥变换器的软开关技术研究较多,一方面通过软开关可以降低器件的开关损耗,另一方面也使其开关频率明显增高,同时有利于减小体积和电磁干扰影响,因此在中、大功率移相H桥变换器上得到了越来越广泛的应用[1-12]。然而,尽管目前移相H桥变换器通过增设辅助电路来达到滞后桥臂开关的零电流通断已取得明显效果,但电路结构尚显复杂,有待进一步完善。现有的相关研究主要采取增设变压器、辅助箝位电路和控制电路的方法[3-6],电路拓扑结构和控制比较复杂;也有的学者采用耦合电感取代变压器,并构成辅助箝位电路,不仅耦合电感设计难度较大,而且其磁芯损耗将随频率和负载增大而加重[7-9];还有的给辅助变压器多增设副边绕组,并通过二极管为电容器充电并实现电压箝位,但存在滞后桥臂开关在负载较轻时难以达到零电流通断的问题,而且多副边绕组会增大变压器的体积与容量[10];变压器副边的箝位辅助电路也有文献报道采用多只二极管和电容器组成,使用无源器件较多,电路结构复杂[11-12];采用副边倍流整流单元结构不失为一种效果较好的选择,电路结构不很复杂,只是需要两只电感器交替工作,电感器的体积较大而利用率较低[13]。笔者利用开关电源原有的变压器和整流、滤波元件,为变压器副边输出侧专门设计一种无源辅助箝位电路,提出移相H桥变换器的一种新型软开关拓扑方案。

1 变换器拓扑及软开关作用原理

所提出的适用于移相H桥变换器的新型无源箝位式软开关电路拓扑如图1所示。与常规的ZVS移相H桥变换拓扑相比,主要加入了由CC、DC和DL构成的副边电压箝位和续流电路。为方便分析比较,仍与常规ZVS移相H桥变换器一样,将Q1、Q2称作超前桥臂,Q3、Q4称作滞后桥臂,C1和C2称作超前桥臂的谐振电容器,Llk为谐振电感器。设变压器原边与两个副边的变比均为n。Uab为两个半桥之间的输出电压,近似代表变压器一次侧电压,Uco代表变压器左侧副边的电压,Urec为副边全波整流输出电压。假设输出滤波电感Lf足够大,可近似为恒流Io。H桥逆变器无论工作于正、负半周,在变压器原侧向负载侧供能阶段,总有D5或D6导通,而DL处于反偏断态,Co上的输出电压经DC为箝位电容器CC充电。这种箝位和续流电路主要具有两种作用:①使超前桥臂Q1、Q2不仅可以实现常规的零电压导通,而且可以零电压关断。比如,在输出正半周Q1、Q4对角导通的稳态下,副边Q6处于通态,DL断态,C1上压降近似为零,原边电流ip除含很小的励磁分量之外,主要为副边负载电流Io反射到原边的负载分量Io/n。此时若令Q1关断,一方面,ip经C1、 C2与Llk谐振续流,另一方面，副边的DL即刻导通续流,而由于Llk及变压器副边等效漏感的作用,D6不会立刻关断,形成D6与DL的换流重叠过程,D6电流迅速向DL换流转移。同时,箝位电压UC=Uco作用于副边,反映到原边与Uin相平衡一大部分, C1端压近似为零,加之换流转移作用使其充电电流减小,C1端压保持为零的时间将延长,足以维持Q1的零电压关断。该过程如图2(a)等效电路所示。②可实现滞后桥臂Q3、Q4的ZCS通断。比如,在Q4开通之前,Q1、Q3导通达稳态,ip已复位到零,D5、D6均断态,Io经DL、DC续流。当Q4导通时,如图2(b)等效电路所示,Uab=Uin,同时,副边形成DL向D6换流,并且换流重叠,箝位电压Uc=Uco又作用于副边,反映到原边与Uin的部分作用相平衡,导致Llk端压较小,使得ip从零上升较缓慢,足以保持Q4为零电流导通。至于其关断过程,由于Q4关断之前与Q1同时导通已达稳态,一次侧电流ip已完全复位到零,D5、D6均断态,Io经DL、DC续流,所以Q4的关断为零电流过程。

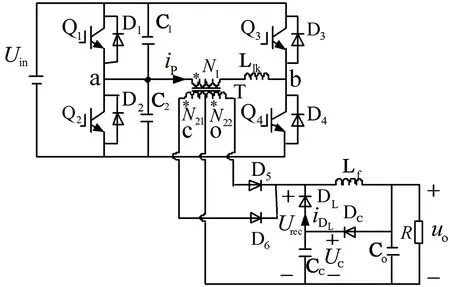
图1 软开关变换电路Fig.1 Proposed converter topology

2 软开关波形及理论分析

设输出滤波电容取值很大,输出电压Uo可近似为恒压源,将软开关H桥变换器的半周期工作过程分解为7个时段分析,有关动态波形如图2所示。

图2 软开关过程等效电路Fig.2 Equivalent circuit of soft-switching process

(1)[t0，t1]时段:在t0时刻前,左上桥臂Q1已处通态,变压器一次侧电流ip复位到零,DC和DL导通续流。当t0时刻开通Q4时,其零电流导通过程如前分析,见图2(b)所示。ip上升速率由下式决定:

ip=(Uin-nUrec)(t-t0)/Llk， t∈[t0,t1].

(1)

其间DL向D6换流发生导通重叠,有关iDL的重叠电流方程为

iDL=Io-nip.

(2)

在重叠期内,由于iDL减小和ip增大,导致UC缓升至峰值,如果CC取值足够大,UC可近似恒压Uo。而且在换流重叠期间近似满足

Uco=Urec=UC.

(3)

这正体现了CC的箝位作用。通常UC=Uo小于Uin/n,与移相角有关。

[t1,t2]时段:在t1时刻一次侧电流ip达到峰值

ip=Io/n .

(4)

iDL下降到零,DL和D6换流重叠结束,DL自然关断于零电流状态,Urec退出受UC箝位的状态,并且有

Uco=Urec=Uin/n.

(5)

本时段原、副边传递能量,同时经DC对CC充电达Uo。

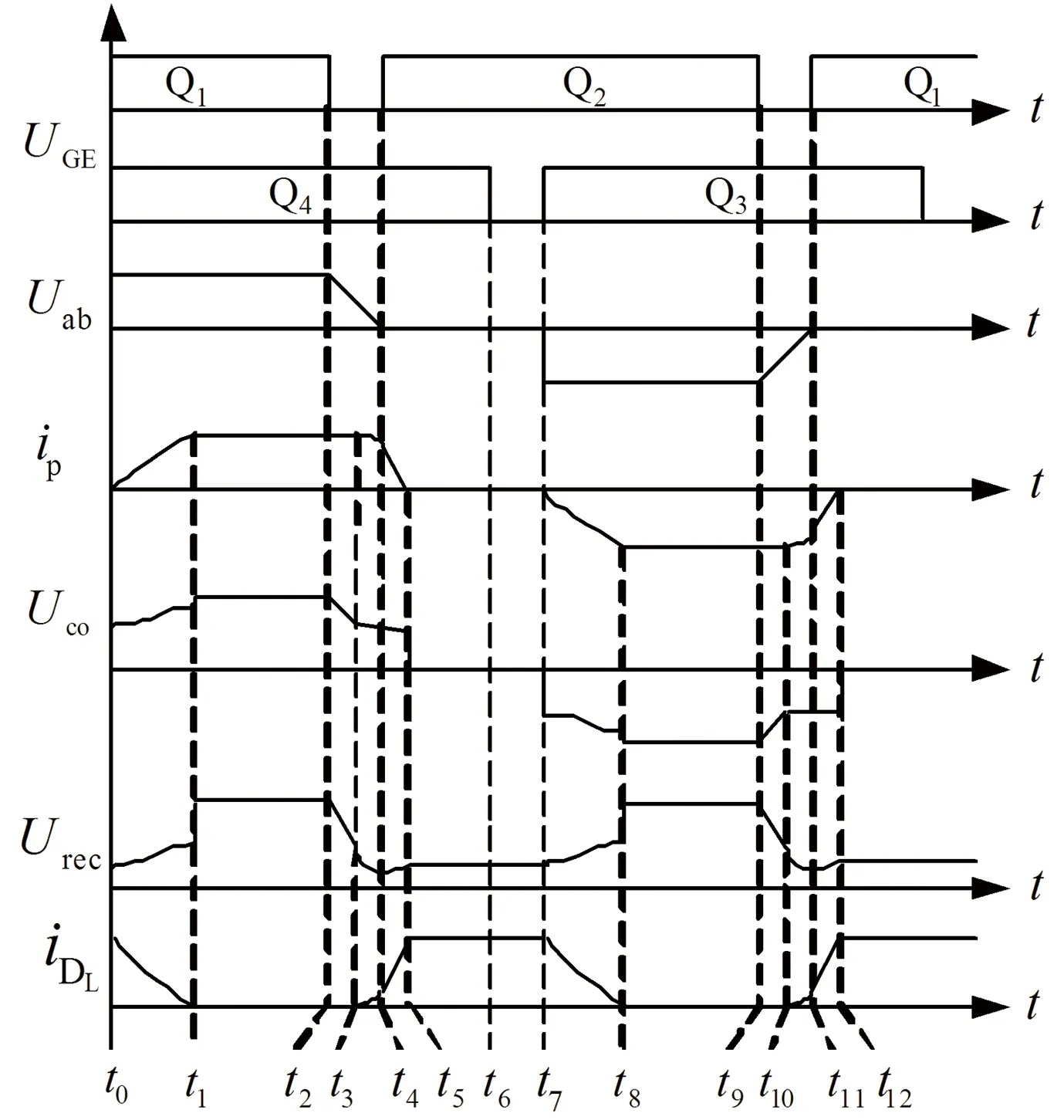
图3 变换器工作波形Fig.3 Operation waveforms of proposed converter

[t2,t3] 时段:在t2时刻令Q1关断,其零电压关断过程如前分析,见图2(a)所示。本时段很短,可认为ip=Io/n是恒值,ip从流经Q1过渡到由C1与C2两支路分流,C2放电,C1充电,其间所转移电荷量

ΔQ=ipΔt=Io(t-t2)/n .

(6)

由式(6)得Uab的变化量:

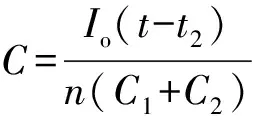
(7)

由式(7)可得

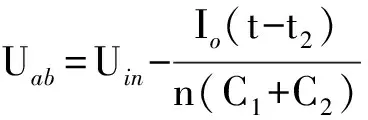
(8)

Uab的降低致使副边的电压Uco和Urec也随之下降,到t3时刻Urec降至UC。

[t3,t4]时段:在t3时刻,Urec下降到UC,DL自然导通于零电压状态,又一次形成与D6的换流重叠,使得Urec再次箝位于UC,并满足式(3)。由于原边和副边反映电压之差在Llk上的作用,ip以下式谐振续流而减小:

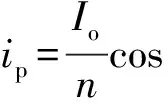
(9)

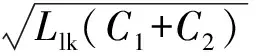
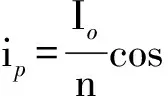
(10)

式中,t4-3表示[t3，t4]段时长。可见，由于箝位电压对原边的反映作用,会使ip下降复位加快。此阶段DC自然会零电压导通。

[t5,t6]时段:在t5时刻iDL达到峰值,ip复位到零,D6自然关断于零电流状态,换流重叠结束。本阶段原副边电压为零,由DL和CC为负载续流。

[t6,t7] 时段:在t6时刻关断Q4,其零电流关断过程如前分析。t7时刻后,H桥工作进入后半周期,其过程分析与前半周期完全对称。

3 软开关条件

3.1 零电压开关条件

鉴于通常开关管的等效结电容很小,在实现超前桥臂开关零电压导通的前提下,其等效电容应适当取大些,故需要外接并联电容器C1和C2,以便降低关断损耗。在[t2，t4]时段,负载最轻时,应使副边滤波电感器Lf折合到原侧,并与Llk共同参与谐振时具有足够能量来保证C1与C2充放电完全,而且能使得上、下桥臂开关之间的死区作用时间td大于uab下降的过渡时间t4-2。因此,由式(8)可知负载电流最小值Iomin与td应满足如下条件:

(11)

3.2 零电流开关条件

本拓扑方案给出的续流和箝位环节应用无源电路可抑制移相输出占空比的丢失[14],亦可防止变压器副侧过冲电压,提高变换效率。通常应选取电容CC足够大,以稳定箝位电压,然而由于输出端的滤波电容Co对原侧电流的复位也有贡献,并且Co一般取容量较大,加之需要限制其回路环流在较低值以内,所以CC在实际设计时不必取太大。假如取CC值足够大,副侧换流重叠使式(3)箝位关系满足,且UC≈Uo。鉴于式(10)及ip在[t4，t5]时段的变化率,为使原侧电流达到完全复位,保证紧接其后的滞后桥臂零电流通断,H桥移相输出的占空比最大值dmax应满足条件:

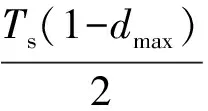
(12)

4 实验结果及分析

采用图1所示新型软开关变换电路,研发了一台实验样机。参数设计中依照式(11)和(12)给出的软开关条件作为设计准则,例如取负载最小电流Iomin=7 A,保证式(11)的两条件都能满足。所选参数如表1所示。

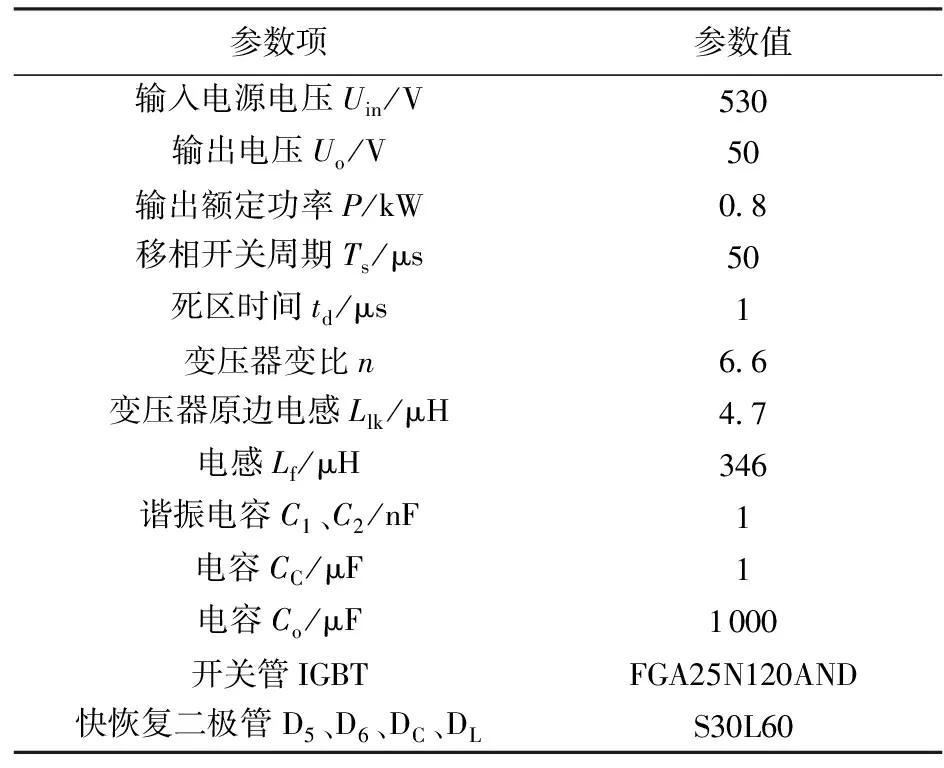
表1 样机参数

由三相二极管整流滤波器提供输入直流电压源Uin。在额定功率一半的负载下以数字存储示波器观察并记录有关软开关电压、电流波形如图4所示,其中图4(a)与(b)分别表明了Q2超前桥臂ZVS导通与ZVS关断的uCE及栅极驱动电压uGE波形;图4(c)与(d)分别表明了Q4滞后桥臂ZCS导通与ZCS关断的iQ4及uCE波形。可见两桥臂开关均工作于软开关通断状态。图5(a)、(b)和(c)分别示出有关副边箝位的uco、urec和iDL、iQ4等电压电流波形,从中可见,对应于一次侧电流的上升与下降时段,副边电压uco形成明显的电压过渡台阶,此时箝位二极管DL正处换流重叠通态,表明此时段uco被箝位于UC,此换流重叠及箝位作用对一次侧电流的加快复位起着关键作用。这也与理论分析相吻合,从而也有效地证实了本拓扑方案及理论分析与参数设计规则的正确性与可行性。

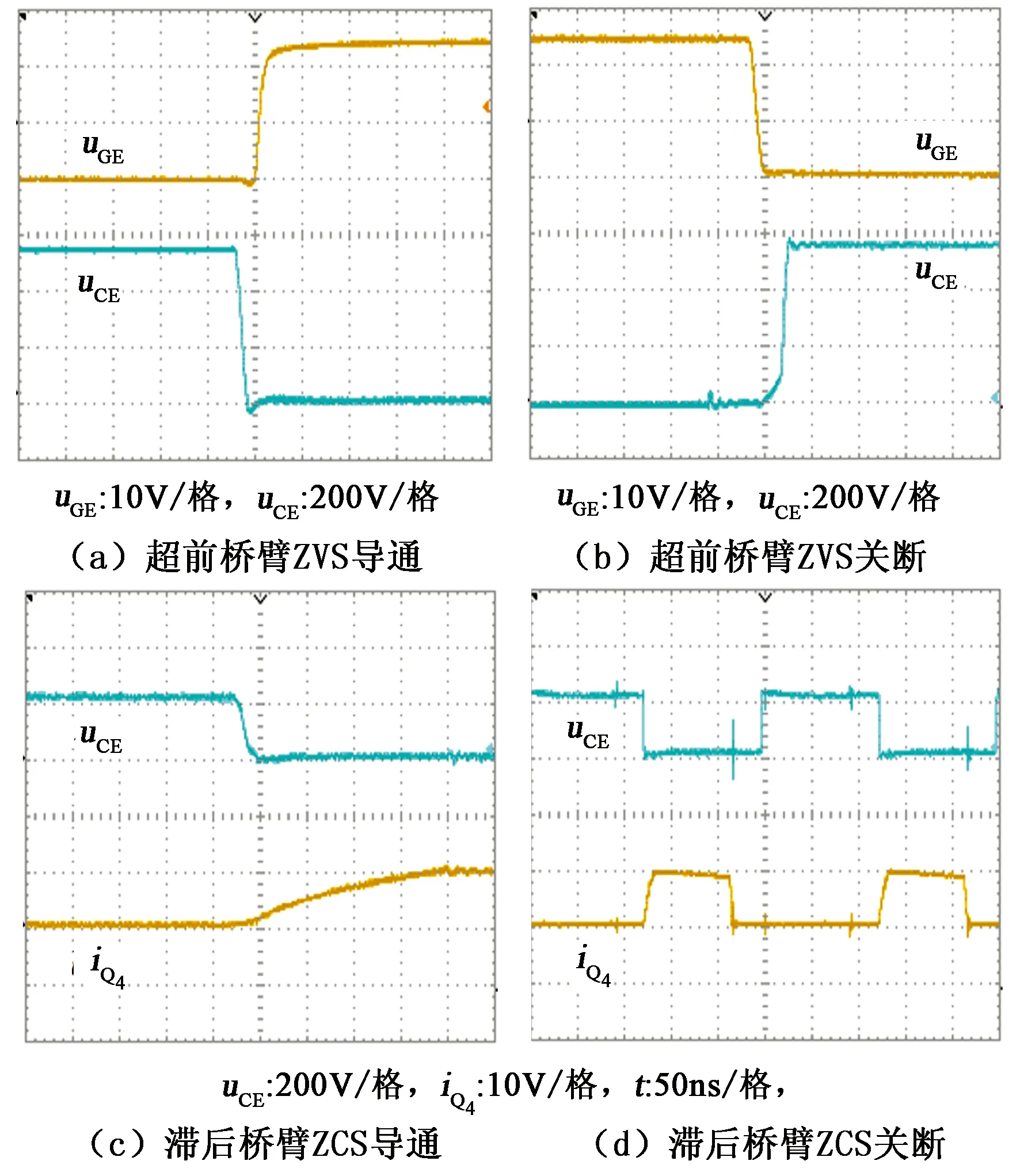
图4 软开关电压、电流波形Fig.4 Soft switching waveforms

对实验样机在不同负载下所绘出的效率曲线如图6所示,可以看到在比较宽的负载电流范围内转换效率优于85%,当负载接近额定电流(16A)的较大范围内效率可达到90%以上,这比同容量的普通H桥变换器效率增大约2%左右[15-16],表明本拓扑方案的实际应用价值比较明显。

图5 副边箝位波形Fig.5 Secondary clamp waveforms

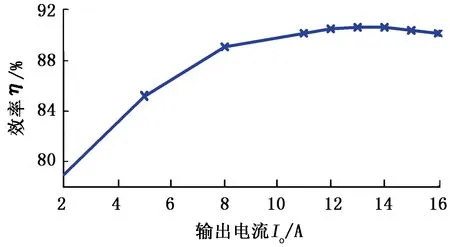
图6 效率曲线Fig.6 Efficiency curve

5 结束语

对新型软开关拓扑进行了原理定性阐述,结合各时段波形进行了理论分析,得出了有关软开关条件,并依此做参数设计,完成了样机实验及波形测试。理论与实验结果表明,所提出的无源箝位和续流拓扑可抑制副边电压过冲和移相输出占空比的丢失问题,而且电路结构简单,性能可靠。其CC箝位电容器通过利用换流重叠与充电作用,能达到工作状态的自适应切换。滞后桥臂的零电流开关效果亦正籍于此箝位作用才得以实现。所提出的移相H桥新型软开关变换拓扑、滞后桥臂开关在全负载范围内均属零电流通断,故其导通和关断过程损耗近乎为零。无源箝位与续流回路中的二极管均为自然通断,电压电流应力小,消除了硬开关存在的动态损耗,静态损耗微不足道。相比有源箝位辅助电路,无源箝位结构简单实用,而且不存在由晶体管驱动带来的有源损耗问题。超前桥臂开关在比较宽的负载范围上既属于零电压导通，又属于零电流导通,因此可视其为零导通损耗。至于其关断过程,在谐振电容并联作用下,易于达到零电压关断,同时由于副边换流转移作用使其开关电流很小,关断过程只存在微弱损耗,近似零电流关断。总之,本变换器软开关拓扑不仅电路简捷、原理清晰,而且明显具备提高效率的作用,适合应用于高性能数字式电源装置等场合。

[1] 周林泉, 阮新波. 二次侧加箝位开关管的ZCS PWM Boost型DC/DC全桥变换器[J]. 电工技术学报, 2006,21(10):81-85. ZHOU Linquan, RUAN Xinbo. A ZCS PWM boost full bridge DC-DC converter with secondary clamping switche[J]. Transactions of China Electrotechnical Society, 2006,21(10):81-85.

[2] 王强,刘岩松,陈祥雪,等. 具有对称辅助电路的谐振直流环节三电平软开关逆变器[J].中国电机工程学报, 2014,34(27):40-49. WANG Qiang, LIU Yansong, CHEN Xiangxue, et al. Resonant DC link three-level soft-switching inverter with symmetrical auxiliary circuits[J]. Proceedings of the CSEE, 2014,34(27):40-49.

[3] 成庶, 陈特放, 余明扬. 一种新型有源次级箝位全桥零电压零电流软开关PWM变换器[J]. 中国电机工程学报, 2008,28(12):44-49. CHENG Shu, CHEN Tefang, YU Mingyang. A novel FB-ZVZCS converter using improved secondary active clamping circuit[J]. Proceedings of the CSEE, 2008,28(12):44-49.

[4] 尹培培,洪峰,王成华,等.无源无损软开关双降压式全桥逆变器[J]. 电工技术学报, 2014,29(6):40-46. YIN Peipei, HONG Feng, WANG Chenghua, et al. Passive lossless soft-switching dual buck full bridge inverter[J]. Transactions of China Electrotechnical Society, 2014,29(6):40-46.

[5] 孙铁成, 郭建辉, 王宏佳, 等. 改进型具有电压箝位的全桥ZVZCS PWM DC/DC变换器[J]. 电工技术学报, 2007,22(7):47-51. SUN Tiecheng, GUO Jianhui, WANG Hongjia, et al. Improved full-bridge ZVZCS PWM DC/DC converter using voltage clamping[J]. Transactions of China Electrotechnical Society, 2007,22(7):47-51.

[6] 陈仲, 刘沙沙, 史良辰, 等. 两种加辅助网络的全桥变换器的损耗对比分析[J]. 中国电机工程学报, 2012,32(18):66-72. CHEN Zhong, LIU Shasha,SHI Liangchen, et a1. Power loss comparison of two full-bridge converters with auxiliary networks[J]. Proceedings of the CSEE, 2012,32(18):66-72.

[7] 孙铁成, 王高林, 汤平华, 等. 基于数字信号处理器控制的新型全桥移相式零电压零电流开关PWM DC-DC变换器[J]. 中国电机工程学报, 2005,25(18):46-50. SUN Tiecheng, WANG Gaolin, TANG Pinghua, et al. Novel full-bridge phase-shift ZVZCS PWM DC/DC converter based on DSP control[J]. Proceeding of the CSEE, 2005,25(18):46-50.

[8] 贺虎成.谐振极软开关逆变器工作模式分析[J].高电压技术,2013,39(3):213-220. HE Hucheng. Mode analysis of a resonant pole soft-switching inverter[J]. High Voltage Engineering, 2013,39(3):213-220.

[9] 许峰,徐殿国,柳玉秀. 一种新型的全桥零电压零电流开关PWM变换器[J]. 中国电机工程学报, 2004,24(1):147-152. XU Feng, XU Dianguo, LIU Yuxiu. A novel zero-voltage and zero-current-switching (ZVZCS) full-bridge PWM converter[J]. Proceedings of the CSEE, 2004,24(1):147-152.

[10] CHO J G, BAEK J W, JEONG C Y, et al. Novel zero-voltage and zero-current-switching full bridge PWM converter using transformer auxiliary winding[J]. IEEE Transactions on Power Electronics, 2000,15(2):250-257.

[11] 孙铁成, 王宏佳, 张学广, 等. 一种采用无源箝位电路的新型零电压零电流开关变换器[J]. 中国电机工程学报, 2006,26(17):72-76. SUN Tiecheng, WANG Hongjia, ZHANG Xueguang, et al. A novel ZVZCS converter using passive clamp circuit[J]. Proceedings of the CSEE, 2006,26(17):72-76.

[12] SONG T T, HUANG N. A novel zero-voltage and zero-current-switching full-bridge PWM converter[J]. IEEE Transactions on Power Electronics, 2005,20(2):286-291.

[13] 陈延明, 王娟, 武江峰, 等. 一种改进的零电压零电流倍流整流变换器[J]. 电工技术学报, 2009,24(12):82-87. CHEN Yanming, WANG Juan, WU Jiangfeng, et al. An improved zero-voltage zero-current switching converter with current-doubler-rectifier[J]. Transactions of China Electrotechnical Society, 2009,24(12):82-87.

[14] 石磊, 朱忠尼, 鞠志忠, 等. 一种新型能量交换式移相全桥电路[J]. 中国电机工程学报, 2008,28(12):112-118. SHI Lei, ZHU Zhongni, JU Zhizhong, et al. A novel topology of energy exchanging pattern PS-FB circuit[J]. Proceedings of the CSEE, 2007,28(12):112-118.

[15] 陈乾宏, 殷兰兰, 王健, 等. 二极管加电流互感器箝位的移相全桥DC/DC变换器[J]. 中国电机工程学报, 2008,28(15):24-31. CHEN Qianhong, YIN Lanlan, WANG Jian, et al. Diodes with current transformer clamped phase-shifted full-bridge converter[J]. Proceedings of the CSEE, 2008,28(15):23-31.

[16] KIM E S, KIM Y H. A ZVZCS PWM FB DC/DC converter using a modified energy-recovery snubber[J]. IEEE Transactions on Industrial Electronics, 2002,49(5):1120-1127.

(编辑 修荣荣)

A new soft-switching topology of phase-shift H-bridge converter

ZHANG Jiasheng, XU Xianghua, CHEN Rong, HAO Xiujie

(CollegeofInformationandControlEngineeringinChinaUniversityofPetroleum,Qingdao266580，China)

In view of the current problems in soft-switching converter with complicated topology and greater consumption, a novel soft-switching topology of phase-shift H-bridge converter was presented. Based on the original transformer, rectifier and filtering elements, a passive auxiliary clamp circuit is added. The circuit topology is simple and easy to implement, and requires no active components and additional control. Both ZVS leading-leg and ZCS lagging-leg are realized adaptively. The converter reduces the consumption and improves the system efficiency effectively. The principle of the new soft-switching topology is elaborated qualitatively. Waveforms on every time interval are analyzed theoretically. The soft-switching conditions are derived. The robustness and feasibility of the new topology and the associated theory analyzing method are verified using experimental results.

phase-shift H-bridge； topology； soft-switching； passive auxiliary clamp

2014-06-12

山东省科技发展计划项目(2013GSF11607)

张加胜(1957-)，男，教授，博士，博士生导师，主要从事电力电子与电气自动化方面的教学与科研工作。E-mail:zjsycy2003@126.com。

1673-5005(2015)01-0182-06

10.3969/j.issn.1673-5005.2015.01.027

TM 921

A

张加胜,徐向华,陈荣,等.移相H桥变换器的一种新型软开关拓扑[J].中国石油大学学报:自然科学版,2015,39(1):182-187.

ZHANG Jiasheng, XU Xianghua, CHEN Rong, et al. A new soft-switching topology of phase-shift H-bridge converter[J]. Journal of China University of Petroleum (Edition of Natural Science),2015,39(1):182-187.