*改进的最近电平调制策略在模块化多电平变换器中的应用

胡文华，董 运，张军仁

(华东交通大学 电气与电子工程学院，南昌 330013)

MMC是一种多电平变换器，最早由德国学者Lesnicar和Marquardt于2001年提出[1]。该变换器具有模块化的拓扑结构，可扩展性强，波形质量好等诸多优点[2-3]，特别适用于牵引供电系统、高压直流输电系统、大功率电机驱动系统等中高功率的应用场合[4-7]。关于MMC的调制策略一直是模块化多电平变换器的研究热点之一[8-12]。该变换器的调制策略主要有两类，即脉宽调制(PWM)和阶梯波调制。其中，脉宽调制最常用的是载波移相调制(CPSPWM)方法，具有良好的输出电压，但其开关频率高、开关损耗大，在子模块数较多时控制过程显得十分复杂[13]。阶梯波调制最常用的为最近电平调制方法，NLM方法开关频率低，控制简单，且子模块数越多输出电压THD越小，适用于大功率场合。但当子模块数较少时，阶梯波不能很好地逼近正弦波，输出电压质量差，谐波含量高[14]。为了解决这一问题，文献[15]提出了一种PWM与NLM相结合的方法(SUPWM)，能够有效提高输出电压质量，但同时会大大增加器件的开关频率。文献[8]提出通过改变NLM中round(x)函数的舍入值可以将输出电平数由N+1增加为2N+1，从而减小了谐波含量，提高了输出电压质量。但这一方法会改变子模块电容的平均电压，并因此导致输出电压幅值的变化。文献[9]提出一种方法，通过在round(x)函数中加入以二倍频正负变化的偏移量，使输出电平数变为2N+1，提高了输出电压质量的同时，保证了子模块电容器的平均电压不变，但未对上下桥臂电压平衡做出处理。

本文采用一种改进的最近电平调制方法，在不改变子模块电容平均电压的情况下，将输出电压电平数增加到2N+1，降低了输出电压的总谐波失真，并且减小了子模块电容电压的波动以及上下桥臂电压均值的差异。最后，通过仿真验证了该调制策略的有效性。

1 MMC基本结构及原理

单相MMC的拓扑结构如图1(a)所示，每一相由上下两个桥臂组成，每个桥臂包含N个相同的半桥子模块和一个桥臂电感。子模块结构如图1(b)所示，由两个IGBT及其反并联的二极管和一个稳压电容组成。在正常工作时，上下两个开关互补导通，每个子模块有投入和旁路两种状态。当VT1导通VT2关断时，电容被投入桥臂电流通路，若此时桥臂电流为正，则对电容进行充电，电容电压升高；若桥臂电流为负，则对电容电压进行放电，电容电压会降低。当VT1关断VT2导通时，电容被旁路，不论桥臂电流是正是负，电容电压都保持不变。

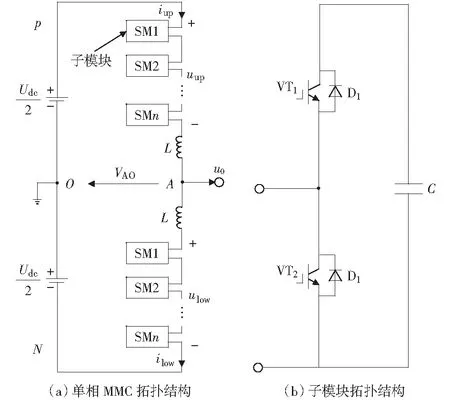
图1 MMC拓扑结构Fig.1 Topological structure of MMC

根据基尔霍夫电压定律和基尔霍夫电流定律可得：

(1)

由于电感L很小，为了方便稳态分析，一般忽略电感压降，得到：

(2)

由(2)可得：

Udc=uup+ulow.

(3)

(4)

式中：uo为交流侧输出电压；Udc为直流侧电压；uup为上桥臂电压；ulow为下桥臂电压。

(5)

式中：m为MMC输出电压调制比；ω为电网电压旋转角速度。

(6)

正常运行时，在一个开关周期内有N个子模块投入，则可得每个子模块电容电压为：

(7)

式中：ud为每个子模块电容电压有效值。

2 传统NLM调制策略

NLM调制方式的本质在于通过控制各个子模块的投切状态，生成阶梯波交流输出电压，并使该阶梯波在任意时刻都尽可能逼近正弦波参考电压。在每个开关周期内上、下桥臂需要投入的子模块数为：

(8)

图2为传统NLM调制策略原理图(以单相，每个桥臂各有8个子模块为例)，根据上下桥臂投入情况，可以得到一个近似于正弦波的阶梯波输出，且桥臂子模块数越多，阶梯波越逼近于正弦波。从图中可以看出，上下桥臂投入的子模块数最小为0，最大为N.当正弦波参考电压不断减小时，上桥臂参考电压增大，投入的子模块数增多。下桥臂参考电压减小，投入的子模块减少，但任意时刻，上下桥臂投入的子模块总数为N.根据式(4)可知输出阶梯波会跟随输出参考电压一起减小。

图2 传统NLM原理图Fig.2 Principle of the conventional NLM method

3 改进的NLM调制策略

3.1 改进的NLM输出特性分析

为了解决上述问题，这里采用一种改进的NLM调制策略。通过在上下桥臂参考电压中同时加入一个偏移量y，使得输出电平数增加。再将偏移量y以输出电压的二倍频率正负变换，来保证子模块平均电压不发生偏离。最后加入上下桥臂的均压控制，减小了上下桥臂电压均值的差异以及子模块电容电压的波动幅度。由于加入了偏移量y，每个桥臂需要投入的子模块数的表达式为：

(9)

图3为改进的NLM调制策略原理图(以单相、每个桥臂各有8个子模块，y取0.25ud为例)。

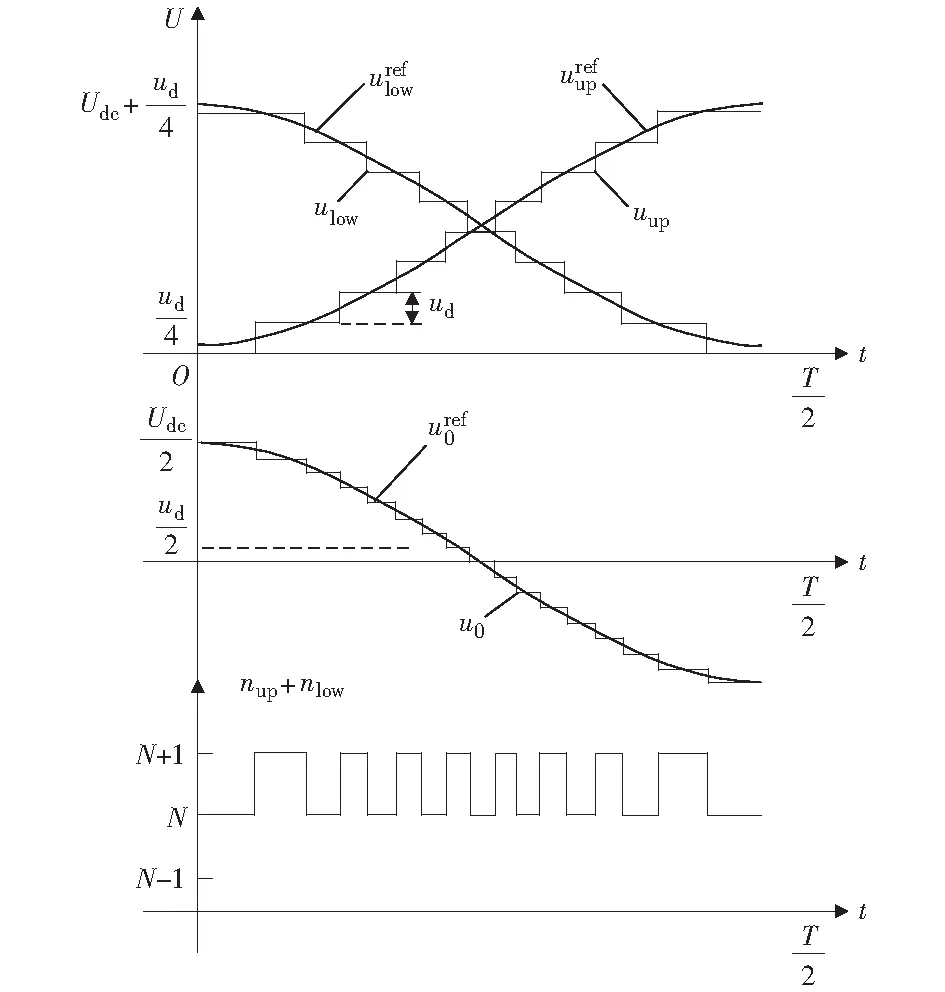
图3 改进的NLM原理图Fig.3 Principle of the modified NLM method

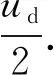
3.2 子模块电容平均电压与偏移量y的关系分析

从图3可以看出，当y>0时，上下桥臂投入的子模块数之和nup+nlow的平均值大于N.同样的，当y<0时，上下桥臂投入的子模块数之和nup+nlow的平均值会小于N.这会导致子模块平均电压发生偏离，从而进一步影响输出电压的幅值。

为了解决这个问题，可以将偏移量y以输出电压的二倍频率正负变换，并选择合适的相位。如图4所示：方波y的频率为输出电压的二倍，(a)中方波与输出电压调制波的相位差为0，(b)中方波与输出电压调制波相位差为π.在一个基本周期中，投入的子模块总数在N+1，N和N-1之间变换，投入的平均子模块数仍为N.当直流侧电压不变时，子模块电容的平均电压不会发生偏离。

图4 投入的子模块数与y的关系图Fig.4 Relation of y and number of inserted submodules

由于输出电压调制波斜率的变化，不同时刻产生的阶梯波宽度也不同。为了保证投入的子模块数平均值为N，y与输出调制波的相位差只能为图4中0或π两种情况。

3.3 桥臂均压控制

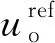
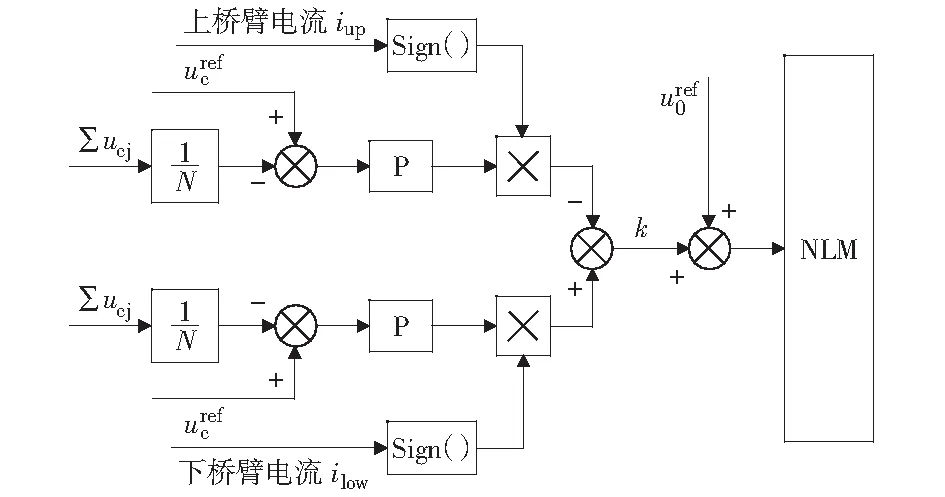
图5 桥臂均压控制策略Fig.5 Control strategy of arm voltage balancing

加入桥臂均压控制后，上下桥臂参考电压变为：

(10)

此时投入的子模块数如图6所示，由于加入偏移量k。a，d和b，c段不再对称。通过调节合适的比例参数，来达到对桥臂电压均值的控制效果，保证直流母线电压的稳定。

4 仿真分析

为了验证本文相关理论结果和所提方法的有效性，在Matlab/Simulink环境下按照图1所示主回路搭建了单相MMC系统，每个桥臂有8个子模块，具体参数见表1.

图6 加入均压控制后投入的子模块数Fig.6 Number of inserted submodules when adding the average voltage control

首先，为了验证本文所采用的改进的NLM调制方法对于提高输出电压质量的有效性。分别将传统NLM方法，文献[8]中NLM方法和改进的NLM方法的输出电压做了对比。仿真结果如图7所示。

表1 仿真参数Table 1 Parameters of the simulation system

从图中可以看出，传统NLM方法输出电平数为N+1，波形质量差。文献[8]中NLM方法和改进的NLM方法输出电平数为2N+1，波形更接近于正弦调制波，波形质量好。但是文献[8]中NLM方法会改变子模块电容的平均电压，从而使uup，ulow的幅值发生变化，由(4)可知输出电压幅值也会发生偏离。而改进的NLM方法可以很好解决这一问题，既可以得到更接近于正弦的输出波形，又保证了输出电压幅值不发生偏离。

图7 3种NLM方法输出电压波形Fig.7 Output voltage waveforms of three NLM method

其次，为了检验本文提出的桥臂均压控制对于减小子模块电容电压波动以及上下桥臂电压均值的差异的有效性。在相同条件下与文献[8]、文献[9]中NLM方法进行了对比仿真。3种控制方法下的仿真结果如图8所示。

从图中可以明显看到，在文献[9]中NLM方法和改进的NLM方法中子模块电容的平均电压保持在额定值附近且电容电压波动幅度较小，而文献[8]方法下的平均电压要大于额定值且电容电压波动幅度较大。并且由于加入了桥臂均压控制，改进的NLM可以更进一步减小子模块电容电压的波动幅度和桥臂电压之间的差异。

图8 三种NLM方法子模块电容电压及上下桥臂电压均值差异波形图Fig.8 Submodule capacitor voltage waveforms and difference between the upper and lower arms average voltage of three NLM method

5 结束语

本文首先介绍了MMC的电路特点及工作原理，在此基础上提出一种改进的NLM方法，通过在桥臂电压参考信号中加入合适的偏移量使输出电压电平数从N+1增加到2N+1，在不增加开关频率的情况下改善了输出电压质量。针对一般NLM方法没有考虑上下桥臂电压的平衡问题，加入了桥臂均压控制。与一般NLM方法相比，能够减小子模块电容电压的波动幅度以及两个桥臂均值之间的差异。最后，通过搭建Matlab/Simulink仿真模型验证了本文提出的改进调制策略的有效性。