基于k/n(G)模型的MMC系统可靠性建模与分析
2020-12-30郑文迪许启东邵振国周腾龙李怡馨曾祥勇
郑文迪,许启东,邵振国,周腾龙,李怡馨,曾祥勇
(1.福州大学电气工程与自动化学院,福建福州 350108;2.福建省电器智能化工程技术研究中心,福建福州 350108;3.中国能源建设集团湖南省电力设计院有限公司,湖南长沙 410007)
模块化多电平换流器(modular multilevel converter,MMC)自提出以来便受到了国内外学者广泛的关注[1-3],目前对MMC 的研究主要围绕子模块(submodule,SM)拓扑结构[4]、控制策略[5]和调制策略[6]及谐波抑制[7]等方面展开.此外,可靠性也是MMC 系统设计和运行时需要考虑的关键因素[8].为了提高MMC 可靠性,在实际工程中通常会进行冗余配置[9].因此,有必要对配置冗余子模块的MMC 系统进行可靠性分析.目前已有相关学者对MMC 可靠性展开相关研究.丁明等基于k/n(G)模型,建立了两电平电压源换流器的可靠性模型,计算了不同电压等级和不同冗余度下的换流阀可靠性指标,并以可靠性指标配置换流阀模块最优冗余数目[10].许建中等提出了基于经典概率理论的具有故障穿越能力的混合MMC的可靠性模型,并基于该模型对三维曲面进行一阶差分,求解出不同子模块拓扑结构的MMC 冗余配置比[11].郭静丽等建立了子模块处于寿命曲线的稳定运行期的可靠性模型,并分别从故障率、电压水平、电压偏差三个角度对MMC 进行综合性能评估[12].然而上述文献都是在各子模块、控制模块可靠性完全独立条件下进行的MMC 可靠性分析,未考虑同一桥臂中各模块间存在的相关特征.而文献[13]通过仿真实验验证了某些子模块发生故障时,同一桥臂上其余子模块的电容电压纹波幅值均受到了不同程度的影响;文献[14]进一步指出,相间环流会流经同一桥臂所有的子模块,子模块的工作状态具有一定的相关性.文献[15-16]假设各子模块间存在相关性,基于Copula 理论建立了MMC 可靠性模型,并在模型基础上计算了MMC 桥臂可靠性.但其主要存在以下两点不足:第一,该方法虽考虑了各子模块间的相关性,但未能给出子模块间的相关系数的确定方法;第二,未考虑桥臂控制模块与各个子模块之间的相关性的研究.文献[17]中明确指出,不同工况下热备用控制策略中算法时间复杂度及空间复杂度不同,导致了相间环流、子模块电容电压波动幅值减小的程度也不尽相同.此外,不同容错控制策略的算法计算量不同,也会导致相应子模块投入时间有所不同,所以,子模块出现故障时会导致其他电容电压纹波出现不同程度变化[18].总而言之,不同的控制策略会导致各个子模块的纹波电压有不同程度的变化.因此,同一桥臂各个子模块及控制模块之间并不是严格独立的,忽略MMC 各模块间相关性,一定程度上会影响实际工程MMC-HVDC 系统的可靠性分析计算结果.
针对上述不足,本文首先在MMC 拓扑结构基础上建立各元件的可靠性模型,充分考虑各个模块间的相关性,并通过极大似然估计法得到相关系数;基于k/n(G)模型建立MMC 可靠性分析模型,进一步讨论在运行年数、相关系数和子模块数量不同时MMC 可靠性变化规律;最后,通过算例分析,得到MMC 可靠性设计和优化的方案.MMC 可靠性建模与分析流程如图1 所示.
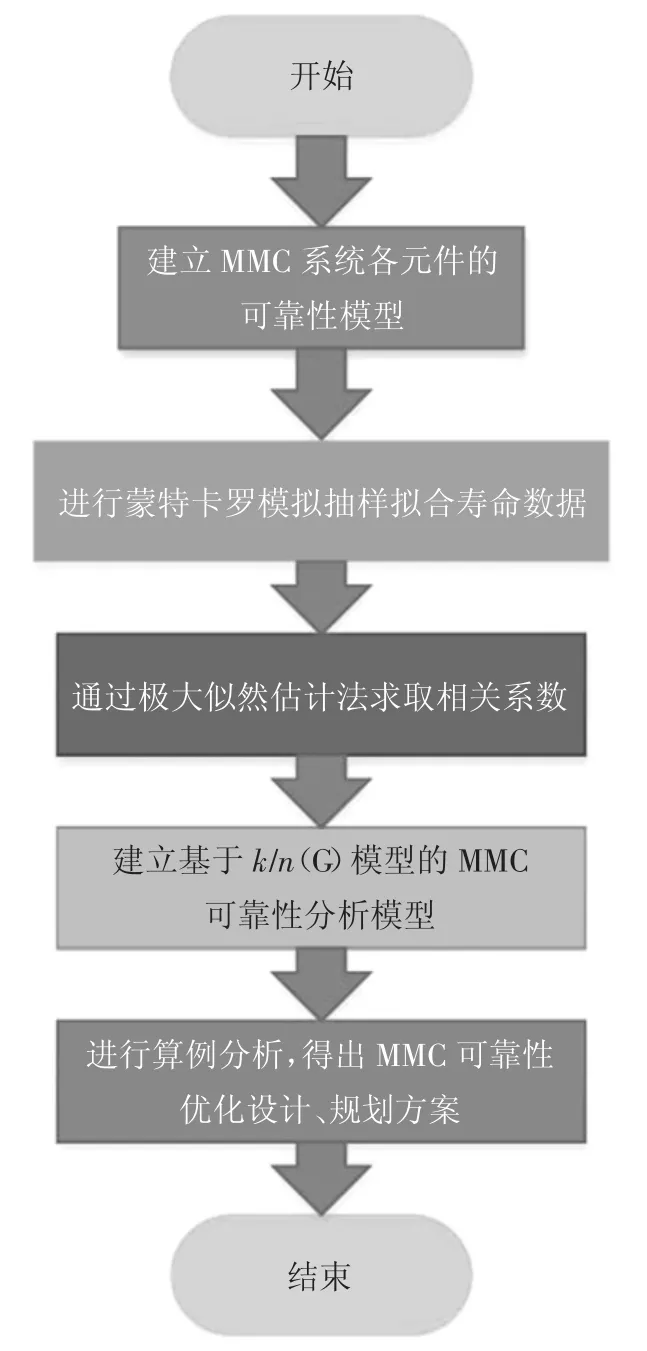
图1 可靠性建模与分析方法流程图Fig.1 Flow diagram of reliability modeling and analysis method
1 MMC 结构
1.1 MMC 拓扑结构
MMC 上、下桥臂分别由N 个必备子模块和N0个冗余子模块级联构成,如图2 所示为直流侧电压,O 为直流侧零电位参考点.目前实际工程应用中,子模块通常采用半桥结构[19],故本文选用半桥结构进行可靠性分析.
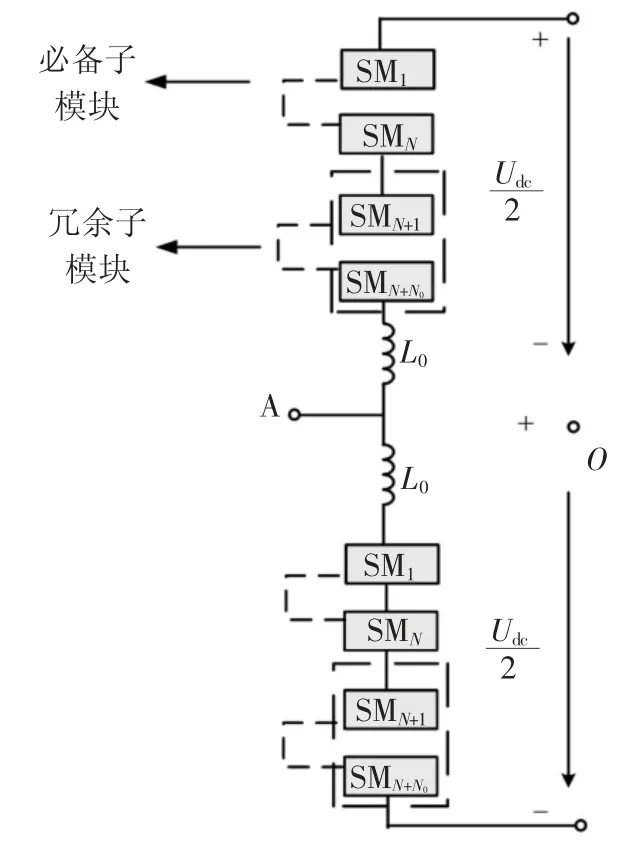
图2 MMC 拓扑结构Fig.2 Configuration of MMC
1.2 子模块结构
每个半桥子模块由2 个IGBT 模块T1 和T2、储能电容C、均压电阻RP和保护开关(旁路开关K1 和压接式封装晶闸管K2)等一次设备以及取能电路、子模块控制器(光纤通信驱动和集成电路)等二次设备组成,具体如图3 所示.
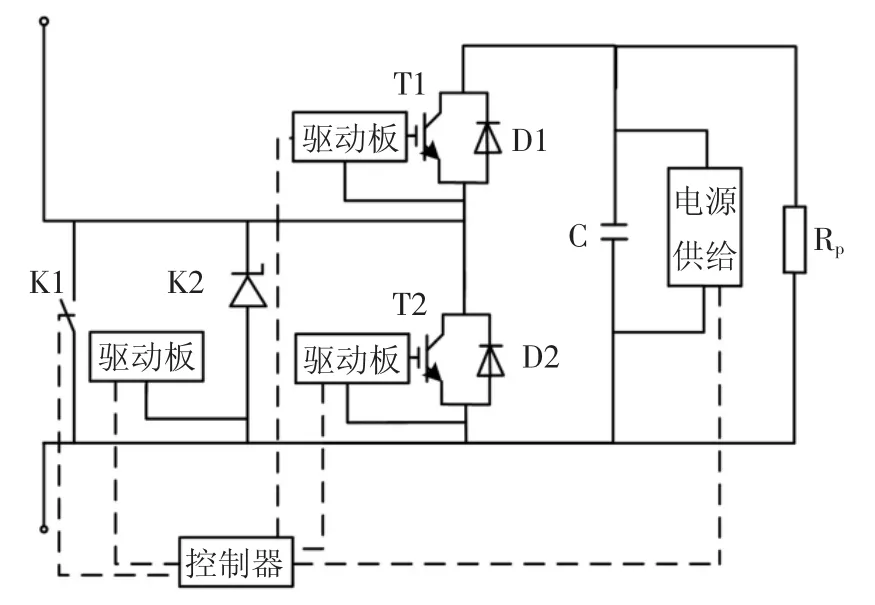
图3 半桥子模块结构示意图Fig.3 Configuration of a half-bridge submodule
2 MMC 模块可靠性分析方法
2.1 Copula 理论
随机变量的联合分布函数能反映变量间的相关特性.因此,对于分析多维变量间的相关性最直接最有效的方法就是求解多维变量的联合分布函数.但若随机变量服从非正态分布,其联合分布函数的显式表达式不易得出[20].而Copula 函数是一类可将变量的联合分布函数与它们各自的边缘分布函数连接到一起的函数,为求解联合分布函数提供了新的思路.
任何一个多维联合分布函数都可由若干个边缘分布函数以及描述相关结构的Copula 函数来表示[21].为了最大限度地反映信息量间的相关性和最简洁的结构[22-23],可以从多个候选Copula 函数中选择生成元为φ1/(1-θ)(t)=(-lnu)1/1-θ的Gumbel-Copula 函数对MMC 进行可靠性分析.二维Copula 函数定义为:
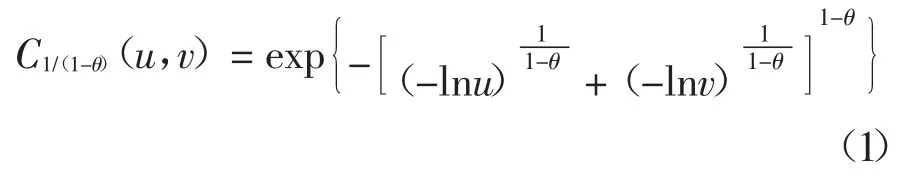
式(1)中,u、v 为随机变量;θ∈(0,1),为随机变量u和v 之间的相关系数.若描述对象为多元联合分布函数,则n 维Gumbel-Copula 函数为:
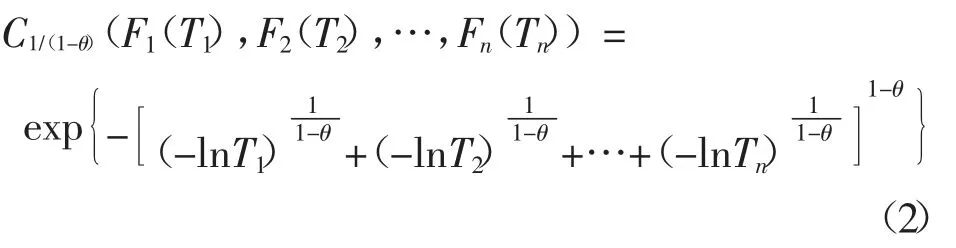
式(2)中,θ=0 表示所有MMC 模块均独立,θ=1 表示所有模块均完全相关,在实际MMC 工程中不可能发生.
Sklar 定理[24]:令F(T1,T2,…,Tn)为具有边缘分布F1(T1),F2(T2),…,Fn(Tn)的N 维联合分布函数,则存在一个Copula 函数满足:
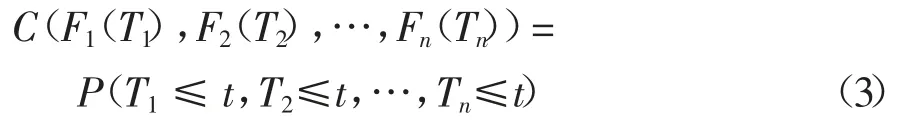
若F1(T1),F2(T2),…,Fn(Tn)是连续函数,则这个Copula 函数是唯一确定的。
2.2 子模块及桥臂控制模块可靠性模型
根据图3 所示的子模块结构以及运行原理,可建立元件的组合关系如图4 所示,子模块的可靠性由IGBT 模块、电容器、均压电阻、保护开关、子模块控制器和电源供给等共同决定.
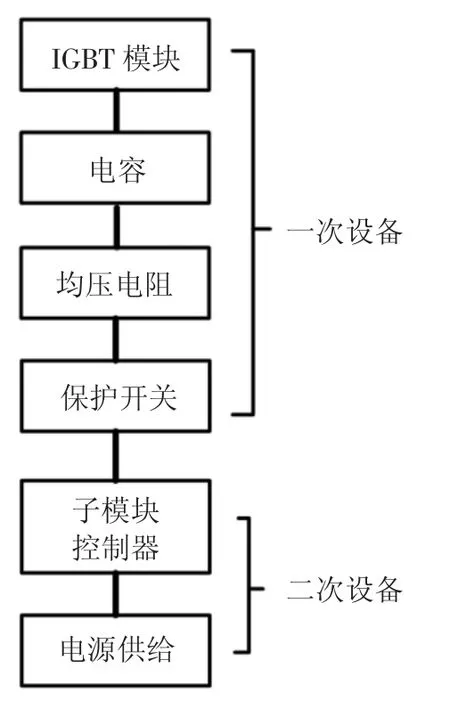
图4 子模块组合关系图Fig.4 Block diagram of submodule
本文假设MMC 元件服从指数分布[25],则子模块可靠性为

式中:RSM、R1、Rcap、RRp、RK、RSMC、RPS分别为子模块、IGBT 模块、电容、均压电阻、保护开关、子模块控制器和电源供给的可靠性函数;而λ1、λcap、λRp、λK、λSMC、λPS和λSM分别是IGBT 模块、电容、均压电阻、保护开关、子模块控制器(光纤通信驱动设备和集成电路)、电源供给和子模块的故障率.
同理,桥臂控制模块的可靠性函数可以表示如下:

MMC 中各元件故障率如表1 所示.
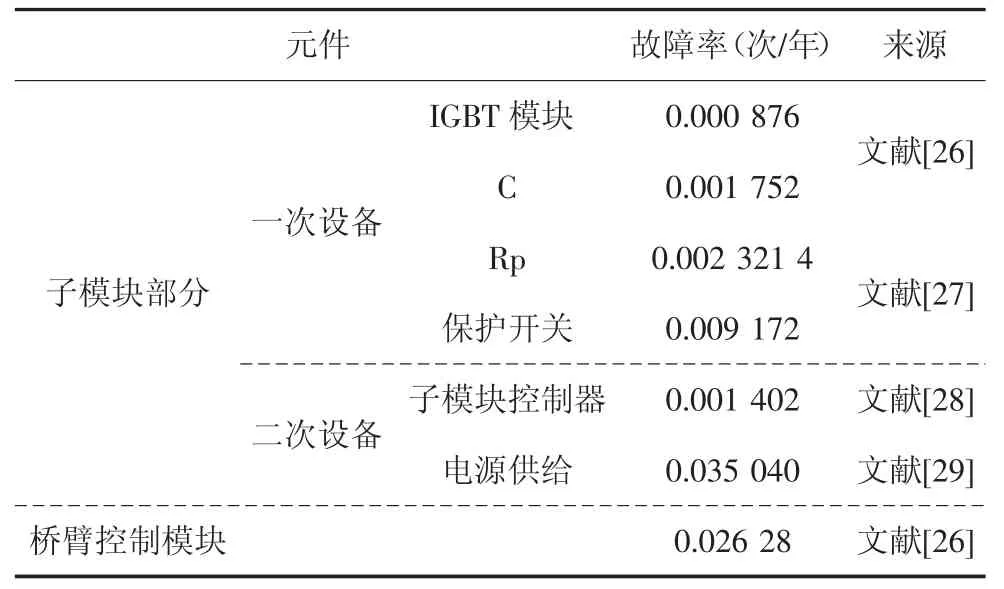
表1 元件故障率Tab.1 Component failure rate data
2.3 相关系数获取方法
假设各个模块间均有相关性,相关系数的获取通常采用极大似然估计[30](Maximum likelihood estimation,MLE).由于世界上第一个MMC-HVDC 工程——Trans Bay Cable 柔性直流输电工程从2010 年才开始投运,从原始的子模块寿命数据获取相关系数暂时无法实现,因此,为了获取模块间的模拟寿命数据,可通过生成多组符合λSM、λcp指数分布规律的MMC 系统关键元件寿命随机数据而获取.
首先利用式(4)(5)求出模块间累积分布函数为:

然后求取F(t)的反函数:

式(7)中,u 为[0,1]间的任意随机数,其服从均匀分布.对u 进行蒙特卡洛随机抽样,用指数分布拟合元件的寿命数据,因此,模块间基于Copula 理论的极大似然函数为:

式中:p 是运行年数;fi(Tit)是子模块的概率密度函数;fcp(Tcp)=是桥臂控制模块的概率密度函数;FN(TNt)=是子模块的累计分布函数;Fcp(Tcp)=1-是桥臂控制模块的累积分布函数;Tit、Tcp分别为第i 个子模块和控制模块的寿命随机变量,i=1,2,…,N.将lnL 极大化,得到L(θ)参数的极大似然估计为:

通过求解式(9)便可以得到MMC 中子模块的相关系数θ,进而确定θ 的范围.
3 基于k/n(G)模型的MMC 可靠性建模
MMC 三相完全对称,上、下桥臂也完全相同,而与子模块密切相关的换流阀基控制系统也可分为上、下桥臂部分,控制器结构也相同,其三相完全对称且具备一定的独立性.因此,本文中MMC 可靠性以一个桥臂的可靠性来表征.
3.1 表决系统可靠性基本计算模型
k/n(G)系统是容错系统冗余特性下可靠性分析领域的主流选择[31].文献[32]和[33]给出了k/n(G)系统的定义:G 系统由n 个元件组成,当k 个或k 个以上元件正常工作时,系统正常运行;当n-k+1 个元件故障时,系统故障,其可靠性示意模型如图5 所示.
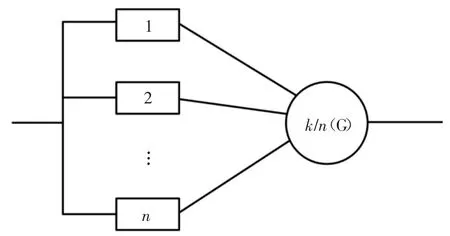
图5 表决系统可靠性框图Fig.5 Voting system reliability block diagram
3.2 计及模块间相关性的MMC 可靠性建模
桥臂模块组合关系如图6 所示.当配置冗余子模块时,由k/n(G)表决系统可得,N+N0个子模块以及桥臂控制模块组成的系统,若有N 个及以上的子模块和桥臂控制模块同时满足要求,此时桥臂正常工作;MMC 不可靠有以下两种情况:子模块故障数量大于N0,桥臂控制模块故障.

图6 桥臂模块组合关系图Fig.6 Block diagram of arm module
如图6 的桥臂模块组合关系所示,利用Copula函数的参数描述模块间的相关程度,能较好地反映桥臂各模块间的非线性相关特性,因此,本文考虑所有模块间相关性用以描述实际控制装置与子模块之间的复杂关系,重点建立计及模块间相关性的MMC可靠性分析模型.
假设初始时刻系统所有元件都处于理想状态且同时开始运行,系统寿命取决于各元件寿命的最小值.借鉴文献[31]中分析冗余配置下系统可靠性的模型,设t 时刻桥臂中有k 个子模块和桥臂控制模块都无故障运行,桥臂中其余的N+N0-k 个子模块故障,当k 大于或者等于N 时,此时桥臂是可靠的,此时定义事件Am:{子模块中有m 个正常工作,另外N+N0-m 个故障,且桥臂控制模块正常,其中m≥N},可靠性概率为RAN(t),且Am包含的基本事件个数为选择数,则配置子模块的桥臂可靠性函数为:
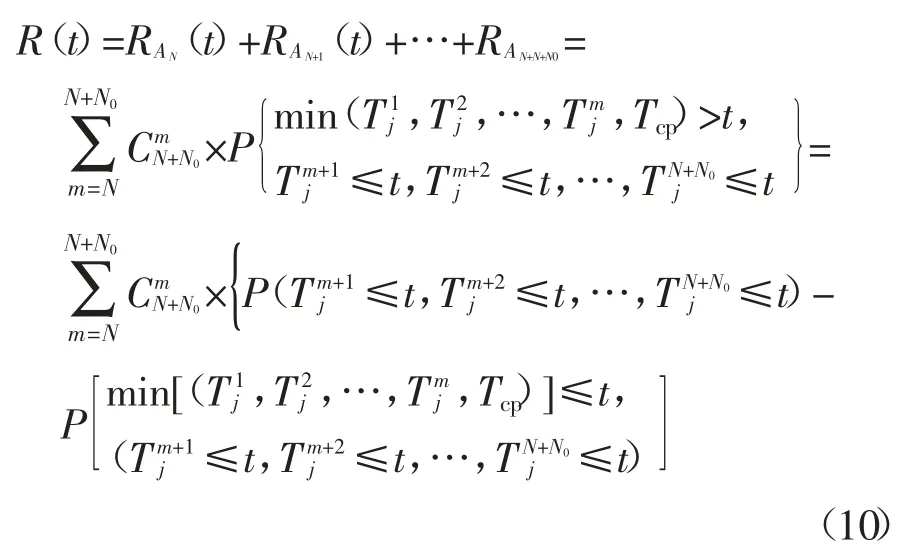
式(10)中,m 表示第j 次从所有子模块中选择的正常工作的子模块个数,且N≤m≤N+N0.

然后利用加法公式和Sklar 定理,可以得到um的表达式为:

同理,xm可以看作ym和zm复合而成的Copula函数;zm可以看成N+N0-k 维的Copula 函数.
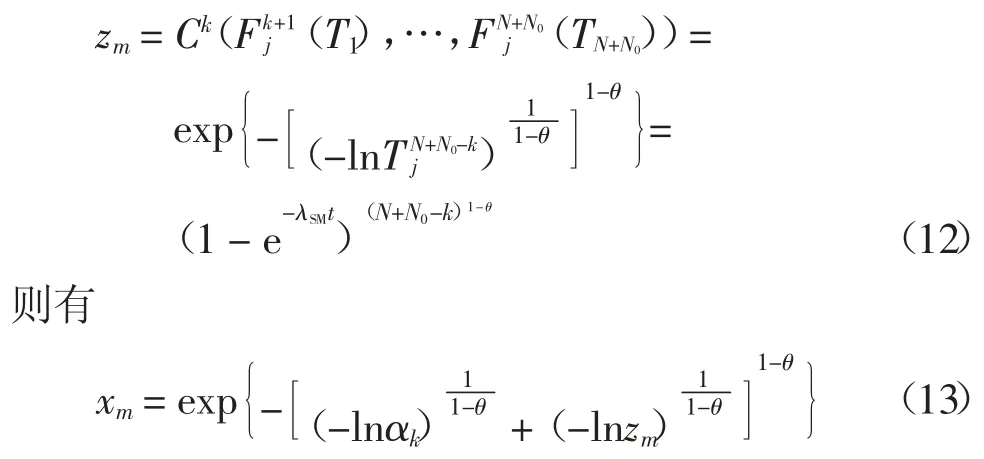
其中,αk=1-um.
因此,配置冗余子模块后的桥臂可靠性为:
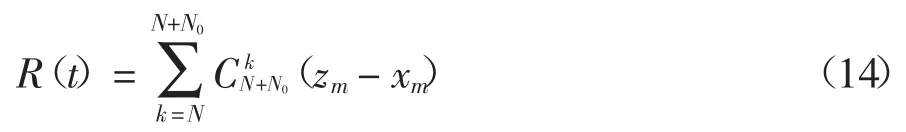
若桥臂上仅有必备的子模块,对比式(11),不难得到其可靠性函数为:
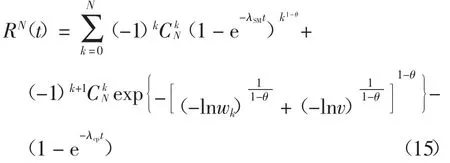
4 算例分析
以某柔性直流输电工程[34]为例进行可靠性分析.该工程每个桥臂有48 个子模块实际投入运行,另配有8 个冗余子模块.通过150 组符合指数分布规律的MMC 子模块和桥臂控制模块寿命数据,代入式(8)中,求得相关系数θ 的平均值约为0.05 且取值范围在0~0.1 之间.下面将在考虑模块间的相关性的基础上,分析MMC 可靠性变化趋势.
首先分析桥臂仅有必备子模块时的可靠性,运行年限t=20,由式(15)可计算出桥臂的可靠度并绘制曲面图,如图7 所示.
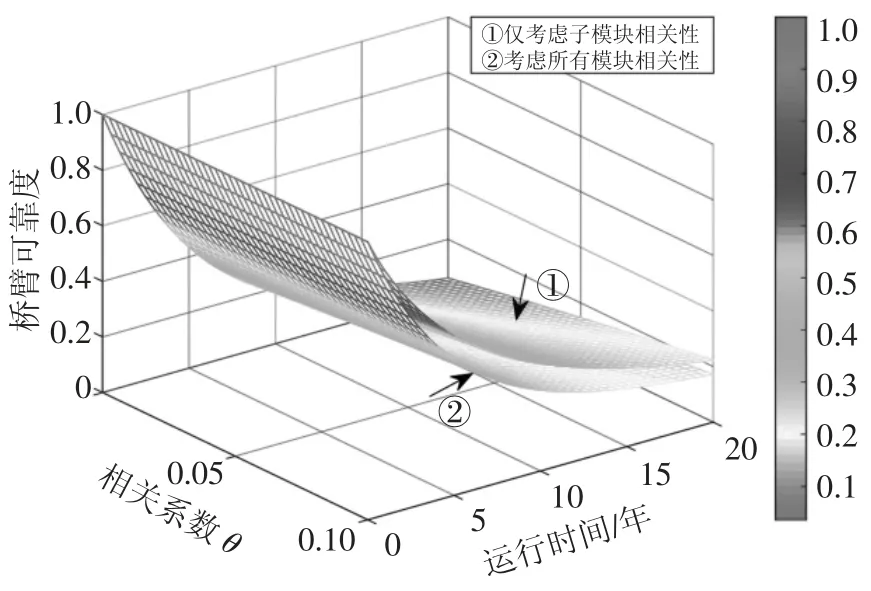
图7 桥臂可靠度曲线Fig.7 Reliability curve of the arm
定义情况①:仅考虑所有子模块相关;情况②:考虑桥臂控制模块与所有子模块间的相关.从图7可看出,随着运行年数的增加,MMC 桥臂可靠性迅速下降,当运行年数t=10 时桥臂可靠度已下降至很低水平,具有6 个桥臂的MMC 可靠性将更低,显然不能满足HVDC 系统的可靠性要求.同时,随着运行年数的增加,情况①与情况②下的桥臂可靠性计算偏差较大,两者可靠度最大差值足有0.18.因此桥臂控制模块对MMC 可靠性有较大影响,在实际工程中应注意检修与防护,延长其寿命,有利于提高系统的可靠性.
由式(15)知,模块间相关性对桥臂可靠性有影响,因此,进一步单独描述相关程度对桥臂可靠性的影响加以分析.桥臂可靠性随运行时间变化如图8所示.从图8 可看出,随着运行时间的增加桥臂可靠性迅速降低,且桥臂的可靠性随着相关系数的增大而增大;对于同一相关系数,情况②的桥臂可靠性将明显低于情况①的桥臂可靠性,并且相差越大越明显,这也证明了忽略桥臂控制模块与子模块之间的相关性将对可靠性计算造成不准确影响.在实际工程的MMC 可靠性设计中,应综合考虑各个模块间相关性的影响,避免MMC 可靠性计算结果不精确.

图8 考虑不同相关程度桥臂可靠度Fig.8 The arm reliability with different levels of relevance
下面进一步分析配置冗余子模块的桥臂可靠性,由式(14)计算得到相应的可靠性数值如表2 所示,并绘制三维曲面如图9 所示.
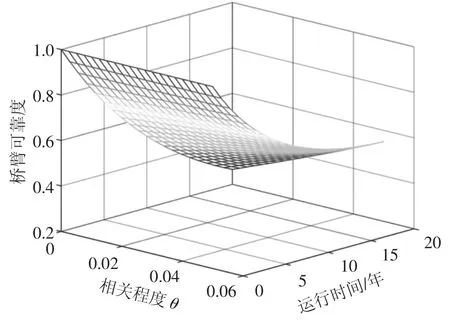
图9 配置冗余子模块的桥臂可靠性Fig.9 The arm reliability with configuring redundant SM
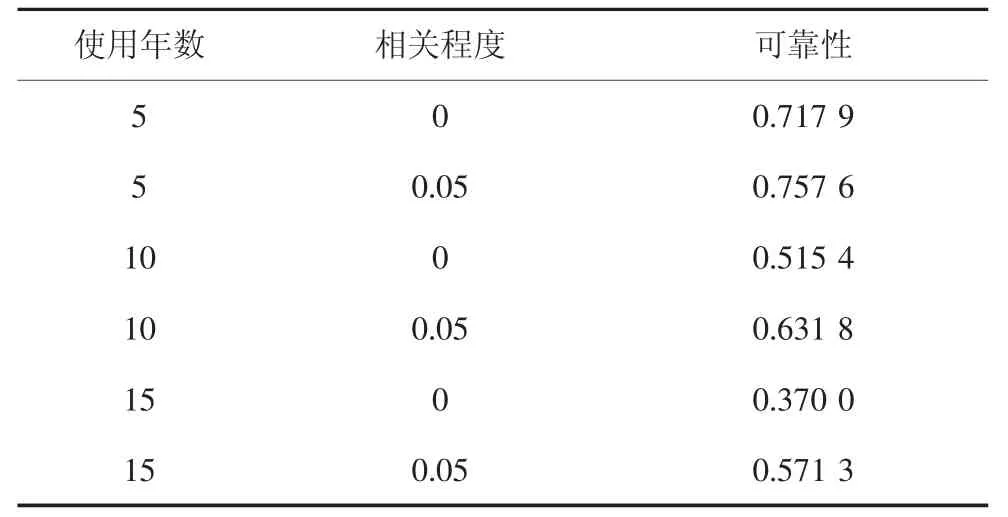
表2 桥臂可靠性Tab.2 Reliability of an arm
结合图9 和表2 分析可知,对于配置冗余子模块的桥臂而言,模块间相关系数越大,桥臂的可靠性越高;当使用时长增加时,桥臂可靠性受相关系数的影响越来越显著.
同样地,分析桥臂可靠度随模块间相关程度的变化情况,其结果如图10 所示.从图10 中可看出,桥臂可靠性随θ 的增大而增大,对于配置冗余子模块的MMC,相关系数越大即相关性越强时,桥臂可靠性越高.其物理解释为:随着模块间相关系数的增加,所有模块寿命的增加或下降的变化趋势将趋于一致,这种趋势降低了桥臂模块间的独立性,换言之,较高相关系数等价于较少数量的等效独立子模块,桥臂的整体可靠性更接近于单个子模块个体的可靠性.因此,综合考虑MMC 各模块间的相关性对设计MMC 可靠性有较大意义.
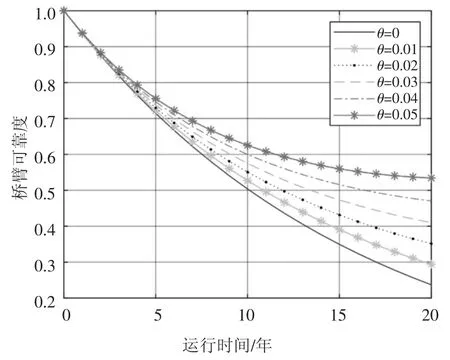
图10 考虑模块间不同相关程度的桥臂可靠度Fig.10 The arm reliability with different degrees of correlation among modules
不同的冗余子模块数目所带来的可靠性增益也不尽相同,需进一步分析不同冗余子模块对系统可靠性的影响,以便确定最佳冗余比.具体地,在表决系统的基础上,取θ=0.05,运行最大时间20 年,计算桥臂可靠度如图11 所示.为了更加直观地研究配置冗余子模块后可靠性的提高情况,选取t=10 时,绘制出配置冗余子模块个数与MMC 可靠性的关系图,如图12 所示.
从图11 中可看出,当子模块冗余度增加时,桥臂可靠度在同一运行年数也相应增加,当配置冗余数量N0=6 时,桥臂可靠度均达到0.5,且配置4 个冗余子模块之后,再增加冗余子模块,对提高可靠性的幅度不大;从图12 可以看出,当MMC 运行年限为10 年,配置4 个冗余子模块时,MMC 可靠性有大幅度提升,超出该范围后再增加冗余子模块,可靠性的改善相对较小,反而导致经济性降低.因此,在算例分析中可以确定提出的可靠性模型的最佳冗余度为8.3%,为进一步扩大可靠性增益,可采用定期维护和检修以保证MMC 系统高可靠性运行.
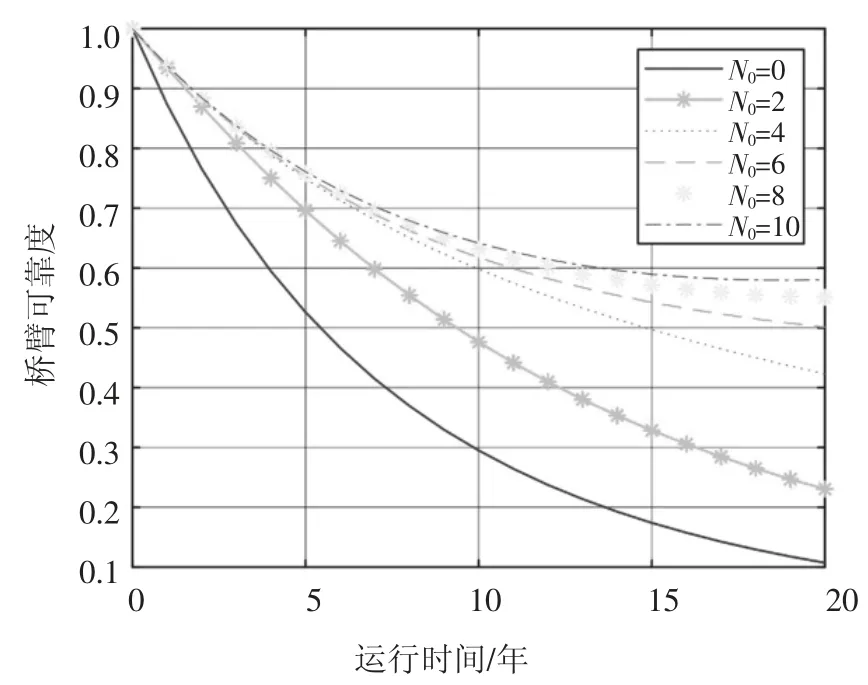
图11 考虑冗余子模块数量的桥臂可靠度Fig.11 The arm reliability changes with redundant SM count
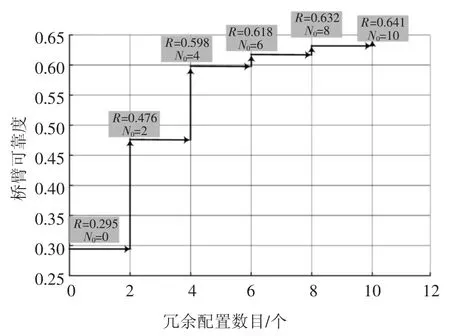
图12 冗余配置后可靠性增益(t=10)Fig.12 Reliability gain graph with redundant configuration
5 结论
本文基于Copula 理论的变量联合概率分布函数构造方法,考虑桥臂控制模块与所有子模块间相关性,建立了基于半桥结构的模块可靠性模型,进而基于k/n(G)模型建立了MMC 桥臂可靠性分析模型.最后,本文就相关程度冗余子模块数量对MMC 桥臂可靠性的影响进行了定量分析,得到如下结论:
1)通过模拟MMC 系统元件的可靠性数据,利用极大似然估计获取模块间的相关系数,解决以往分析中无法反映模块间相关程度的问题.随着实际运行的可靠性数据愈加饱满,本文方法也将为MMCHVDC 提供模拟数据的模型.
2)实际工程中综合考虑MMC 各个模块间的相关性,可进一步提升可靠性分析的精确性.
3)考虑模块间相关性时,算例反映了设置冗余比为8.3%,对MMC 系统可靠性有较大幅度提高,可在工程设计阶段为其提供参考;同时,在MMC 运行一段时间后,冗余配置对提高MMC 可靠性贡献不大,反而应注意投入人力、物力对现役设备进行维护.
