波浪作用下海底管线局部冲刷临界条件

张芝永，刘光生，曾剑

(1.浙江省水利河口研究院浙江省河口海岸重点实验室，浙江杭州310020;2.浙江大学建筑工程学院，浙江杭州310058)

海底管线作为海洋油气开发的重要组成部分，是长距离输送油气最经济的方式之一，它被称为“海上生命线”。海底管线附近的水动力条件引起的海底管线局部冲刷是造成管线事故的一个主要原因。目前，许多学者对于海底管道的局部冲刷问题做了大量详细、系统的研究，但这些研究所针对的问题主要集中在海底管道局部最大冲刷平衡深度［1-4］及局部冲刷发展历程［5-10］方面。在冲刷机理方面，Chiew［11］应用物理模型试验对发现管涌是引起管线冲刷的主要因素，Sumer等［12］根据管涌发生的临界条件，通过物理试验得到了水流、波浪作用下的管线冲刷临界条件。Zang等［13］利用数值手段对波浪、水流作用下管线冲刷的临界条件进行探讨。Zhang等［14］基于多孔介质假设，建立了海床渗流场数值模型，通过与前人试验结果对比验证了该方法的可靠性。

综上所述，虽然文献［13］基于数值模拟方法对波浪作用下冲刷临界条件进行了研究。但文献中提到的数值模拟方法需要分别求解水动力场和渗流场，整个过程较为繁琐，而且其未考虑水面变化和垂向流速的影响，与实际情况有差别。鉴于此，本文提出了一种联合求解水动力场－渗流场的新方法，该方法将海床假设为多孔介质，然后通过对控制方程N-S方程中添加源项来实现海床沙颗粒对流体的阻滞作用，这样水动力场和渗流场就可以通过求解形式大致相同的控制方程来得到。在此基础上，根据线性波理论和VOF方法，对波浪作用下海底管线周围水动力场和渗流场进行耦合求解。

1 数学模型

1.1 水动力控制方程

无论是水动力场还是渗流场，其控制方程均为雷诺平均N-S方程，包括连续性方程和动量方程。连续性方程:

动量方程:

其中:

式中:u为流体速度;i，j取值1，2;ρ是流体的密度; P是作用在流体微元上的压力;ν是流体的运动粘滞系数;是i方向速度脉动值;为雷诺应力张量;νT紊流运动粘滞系数;k为紊动能;δij是克罗内克尔符号。

1.2 湍流模型

紊流模型采用标准k-ε模型，k方程:

ε方程:

式中:ε为耗散率;Gk是由于平均速度梯度引起的湍动能k的产生项;μ是流体粘度;μt是紊动粘度; C1ε和C2ε为经验常数，取C1ε=1.44，C2ε=1.92;σk和σε分别是与湍动能k和耗散率ε对应的Prandtl数，取σk=1.0，σε=1.3。

1.3 多孔介质模型

对于海床区域内渗流场的求解，可将海床视为均匀、各向同性的多孔介质，在动量方程(2)添加1个动量阻滞源项来实现海床泥沙颗粒的阻滞作用，该动量源项公式为

式中:等式右边括号内第1项为粘性损失，α为粘滞阻力系数;等式右边括号内第2项为惯性损失。由于海床中渗流流速都是比较小的，其惯性损失也较小，因此在这里只考虑粘滞损失，忽略惯性损失。粘滞阻力系数α定义为

式中:dp为泥沙平均粒径，在这里用中值粒径d50代替;n为孔隙率。

1.4 边界造波法

对于波浪模拟，本文通过给定入口边界的流速及波高时程变化来进行造波，根据线性波理论，入射边界处的水平速度、垂向速度和水深可以表示为

式中:ω=2π/T，A、k、h、T分别为波浪波高、波数、静水深和周期。

1.5 消波边界

对于数值模拟来说，不可能把整个海域都作为计算区域，需要在计算域末端将波能消去，以避免反射回的波浪影响计算结果的准确性。在数值波浪水槽中可采用阻尼层吸收边界条件处理开边界，使波浪在阻尼层内衰减，从而消除反射波。在这里阻尼层靠近下游出口位置，阻尼层的长度约为2～3倍的波长。阻尼层内动量方程中源项和衰减系数分别取如下形式:

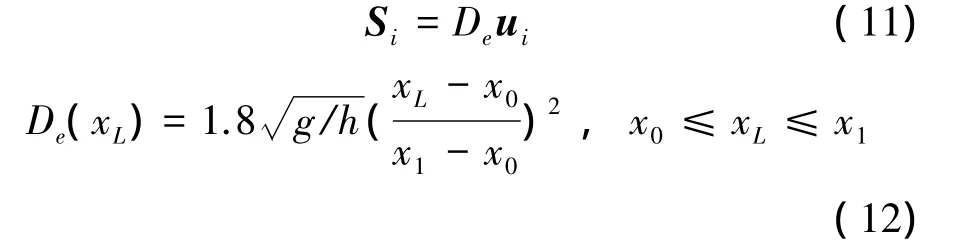
式中:x0为阻尼层的起点横坐标，x1为阻尼层的终点横坐标，xL为阻尼层内任意点的横坐标。

2 水动力场－渗流场耦合模型验证

2.1 模型验证1

本文首先对水流作用下管线周围水动力场－渗流场进行联合数值求解来验证本耦合模型的可靠性，然后在此基础上将水流条件改为波浪条件，对波浪作用下的水动力场－渗流场进行验证。

为便于对比，计算中采用无量纲的压力系数，其公式为

式中:p为计算区域内任意一点压力;p0为参考压力，在这里取初始静水压力;u0为速度入口水面位置处流速，波浪情况时将u0改为近底最大流速umax。

Chiew应用物理模型试验对海底管线冲刷机理进行了研究并对部分埋入海床的海底管线表面压分布进行了测量。在这里选取其中一个工况来对本文的水动力场－渗流场耦合模型进行验证。该工况为来流流速为 0.4 m/s，水深为 0.3 m，管线直径0.05 m，相对水深为6.0，水面变化不大，因此在这里不考虑水面的变化。其管线埋深为0.5D，试验泥沙粒径为1.7 mm，密度ρs取2 600 kg/m3，孔隙率n= 0.43，根据太沙基公式，发生管涌流土的临界水力梯度为

式中:s为泥沙比重，s=ρs/ρ。将参数代入上式得到海床的临界水力梯度ic约为0.91。

上游入口边界和下游边界到管线中心位置的距离均为20D，水流计算区域水深取6D，渗流计算区域竖直方向距离取8D，整个计算区域采用结构化网格进行离散。

控制方程采用有限体积法进行离散，压力和速度采用SIMPLE算法进行耦合求解，在水流区域内求解标准N-S控制方程的同时，海床区域内渗流场通过求解添加了阻滞源项的控制方程。

图1为管线周围海床内外流场图，以管线最上游端为0°起始位置，顺时针方向逐渐增大。这样管线最顶端位置为90°，管线最下游端位置为180°。从图中可以看出，在海床以上，水流自由流动，由于管线的阻挡发生绕流现象，在管线后方出现一较大的涡，而在管线前方根部同样出现一个较小涡体。而在海床内，由于上下游压差的存在，渗流由管道上游流向管道下游。而且由于阻滞作用速度较小，并未出现涡旋。图2为管线表面压力分布情况，可以看出计算结果与试验结果的规律较为一致，在裸露管线部分(0°～180°)内，其最大压力位于海床以上管线迎流面范围(0°～45°)，在接近90°位置，即管线最顶端位置，压力最小。在掩埋管线部分(180°～360°)内，管线表面压力分布与裸露部分压力分布完全不同，表面压力沿着360°～180°的弧线方向逐渐减小。而且从曲线上可以看出两端点位置即180°和360°位置的压力变化率要大于掩埋管线部分的其他的位置。这说明两端点处的水力梯度要大于其他位置的水力梯度，通过求解，下游端渗流出口处水力梯度为0.27，明显小于管涌发生的临界水力梯度0.91，因而在掩埋0.5D情况下，冲刷不会发生。这一结论在试验中得到了验证。

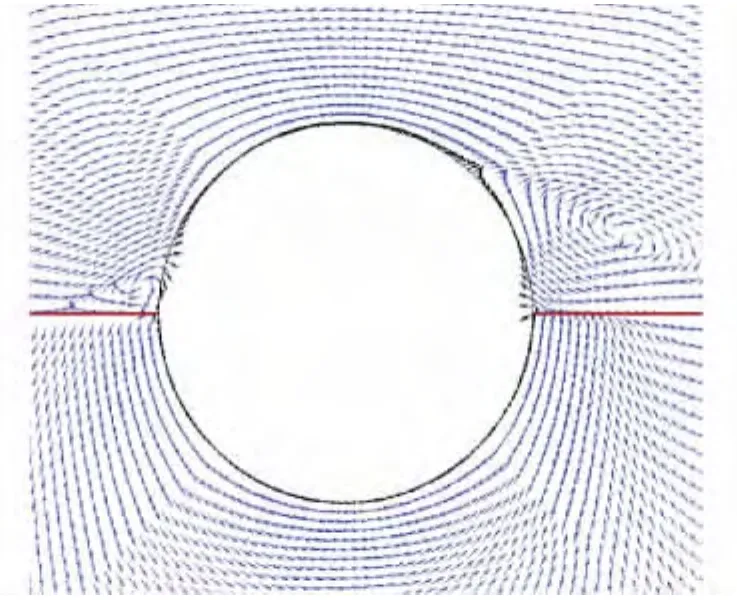
图1 管线周围流场图Fig.1 Flow vectors around pipeline

图2 管道表面压力分布情况Fig.2 Pressure distributions along the pipeline surface

2.2 模型验证2

应用Sumer的试验来进行波浪作用下的水动力场－渗流场模拟验证，具体参数:管线直径D为0.1 m，管线埋深0.064D，波高A为0.17 m，周期T为4 s，水深0.33 m，整个计算区域长度为6倍的波长，管线位于中间位置。计算区域采用结构化网格进行离散。

图3为管线上下游端的压差变化情况，可以看出数值模拟结果与试验结果基本吻合，在波浪作用下管线两端压差周期性变化，在正压差情况下，渗流由管道上游向下游流动，负压差情况下，渗流则由管道下游向上游流动，由图3发现，正压差幅值要大于负压差幅值，因此取压差为最大幅值时的管线表面压力分布，然后依据水流条件下的水力梯度求解过程即可得到该波浪工况下的最大水力梯度值。当这一水力梯度小于管涌发生的临界水力梯度时，冲刷不会发生。

图3 上下游端压差变化情况Fig.3 Pressure difference between upstream and downstream point

3 结果分析

应用上述模型对不同波浪、不同埋深情况下的管线周围水动力场－渗流场进行耦合求解。

3.1 波浪KC数对压差影响

对于波浪来说，常常用无量纲KC(Keulegan Carpenter)数来表示其特征要素，其定义为

式中:umax为近底最大流速，其雷诺数Re=umaxD/ν，范围在16 699～45 058，属于紊流范围。

图4 压差系数随KC变化情况Fig.4 Variations of pressure difference coefficient with KC

3.2 相对埋深e/D对压差影响

埋深不同的管线两端压差系数大小也有所不同。图5为不同埋深情况下压差系数的变化规律。可以看出，相同KC下，随着管道埋深的加大，裸露在水流中的管道高度越来越小，其对水体的阻流作用也越来越小，因此其压差系数随着埋深的加大而逐渐减小。而且呈现近似线性递减关系。

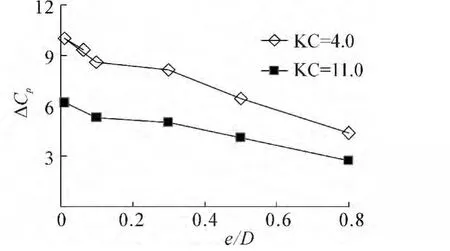
图5 压差系数随相对埋深e/D变化情况Fig.5 Variations of pressure difference coefficient with relative buried depth e/D

3.3 水力梯度分析

当管线两端压差达到最大时，依照恒定水流条件下渗流出口处水力梯度求解方法，对管线表面压力沿着弧长进行求导，然后通过换算即可得到各工况下渗流出口处最大水力梯度，图6列出了KC=11时，不同埋深情况下渗流出口处最大水力梯度的变化情况。从图6中可以看出，随着埋深的加大，由于两端压差的减小和渗流路径的加长，其水力梯度急剧减小。图6中虚线为管涌渗透破坏临界水力梯度曲线，该曲线与水力梯度－埋深关系曲线交于一点，在该点处，其最大水力梯度正好等于渗透破坏临界水力梯度，因而此点即为管涌乃至冲刷的临界点，在该点左侧，其水力梯度大于临界水力梯度，因而冲刷均发生，而在右侧则小于临界水力梯度，冲刷并未发生。这样通过画出不同KC情况下的最大水力梯度随埋深变化曲线，并结合管涌临界水力梯度值，即可通过这种图解方法得到其临界条件。

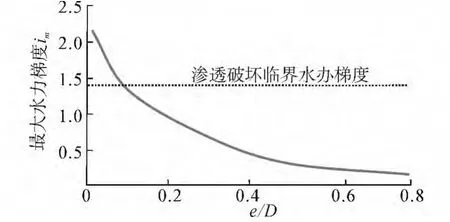
图6 渗流出口处水力梯度随埋深e/D变化情况Fig.6 Variations of hydraulic gradient with e/D

3.4 冲刷临界条件

利用3.3节中方法对不同KC时的管线冲刷的临界条件进行了研究。临界条件不仅与埋深e/D、KC有关还与泥沙性质有关。Sumer等定义了与泥沙性质相关的一个无量纲临界流速:

在这里同样采用该无量纲临界流速来进行分析，图7中列出了不同情况下无量纲临界流速随KC和埋深的变化情况。可以看出数值计算结果与Sumer等［12］的试验结果基本吻合。由前述分析可知，管线埋深越深，管线对流体的阻碍作用越弱，管线两端压差越小，进而导致渗流出口处水力梯度较小，在这种情况下要引起冲刷就必然增大水动力条件。因此，随着管线埋深的加大，其无量纲临界流速也在逐渐增大。对于固定埋深的情况，随着KC的增大，压差逐渐减小，因而其临界无量纲流速也是需要逐渐增大，Sumer指出当KC趋向很大时，其冲刷临界流速趋于恒定流条件下的冲刷临界流速。对于恒定流条件下的临界流速，其经验公式为

而图7中不同KC情况下的临界流速随KC近似线性变化，因此在这里利用KC对式(17)进行拟合修正得到波浪作用下无量纲临界流速的近似计算公式:

通过图7可以看出拟合公式的计算结果与数值计算结果比较接近，而且反映出了无量纲临界流速随KC和埋深的变化规律。这说明可以应用此公式来进行波浪作用下冲刷临界条件的计算。

4 结论

基于多孔介质假设和边界造波法，建立了波浪作用下海底管线周围水动力场－渗流场耦合数值模型。通过与前人试验结果对比验证了耦合模型的可靠性。在此基础上，应用该模型波浪作用下海底管线冲刷临界条件进行了研究，结果表明:

1)当KC＜20时，随着KC的增大，管线两端压差系数急剧减小，而在KC≥20后，压差随KC的变化幅度越来越小并逐渐趋于稳定;

2)相同KC情况下，随着埋深的加大，压差系数近似线性递减，而渗流出口处水力梯度则明显减小。

3)波浪作用下管线冲刷无量纲临界流速随着KC和埋深的增加而均增大，其值可通过式(18)近似求得，这为实际工程中海底管线防护决策提供了技术支持。

［1］SUMER B M，JENSEN H R，FREDSE J.Effect of lee-wake on scour below pipelines in current［J］.Journal of Waterway，Port，Coastal，and Ocean Engineering，1988，114 (5):599-614.

［2］MONCADA-M A T，AGUIRRE-PE J.Scour below pipeline in river crossings［J］.Journal of Hydraulic Engineering，1999，125(9):953-958.

［3］DEY S，SINGH N P.Clear-water scour depth below underwater pipelines［J］.Journal of Hydro-environment Research，2007，1(2):157-162.

［4］李宁，谷凡.海底管线局部冲刷平衡深度Chao解析法的改进［J］.大连海事大学学报，2012，38(1):77-80.

LI Ning，GU Fan.Improvement of Chao-Hennesy analytical method for estimating the equilibrium depth of local scour around submarine pipeline［J］.Journal of Dalian Maritime University，2012，38(1):77-80.

［5］BRRS B.Numerical modeling of flow and scour at pipelines［J］.Journal of Hydraulic Engineering，1999，125(5): 511-523.

［6］LI Fangjun，CHENG Liang.Numerical model for local scour under offshore pipelines［J］.Journal of Hydraulic Engineering，1999，125(4):400-406.

［7］LIANG Dongfang，CHENG Liang，LI Fangjun.Numerical modeling of scour below a pipeline in currents:partⅡ.Scour simulation［J］.Coastal Engineering，2004，52(1): 43-62.

［8］GAO Fuping，YANG Bing，WU Yingxiang，et al.Steady current induced seabed scour around a vibrating pipeline［J］.Applied Ocean Research，2006，28(5):291-298.

［9］文君锋，勾莹，宋伟华，等.海流作用下海底管道局部冲刷数值分析［J］.海洋工程，2012，30(1):75-82.

WEN Junfeng，GOU Ying，SONG Weihua，et al.Numerical examination of steady current-induced local scour around submarine pipeline［J］.The Ocean Engineering，2012，30 (1):75-82.

［10］张芝永，拾兵.泥沙局部冲淤二维数值模拟仿真［J］.哈尔滨工程大学学报，2013，34(2):145-150.

ZHANG Zhiyong，SHI Bing.Two-dimensional numerical simulation on local mud＆sand erosion and deposition［J］.Journal of Harbin Engineering University，2013，34(2): 145-150.

［11］CHIEW Y M.Mechanics of local scour around submarine pipelines［J］.Journal of Hydraulic Engineering，1990，116 (4):515-529.

［12］SUMER B M，TRUELSEN C，SICHMANN T，et al.Onset of scour below pipelines and self-burial［J］.Coastal Engineering，2001，42(4):313-335.

［13］ZANG Zhiping，CHENG Liang，ZHAO Ming，et al.A numerical model for onset of scour below offshore pipelines［J］.Coastal Engineering，2009，56(4):458-466.

［14］ZHANG Zhiyong，SHI Bing，GUO Yakun，et al.Numerical investigation on critical length of impermeable plate below underwater pipeline under steady current［J］.Science China(Technological Sciences)，2013，56(5):1232-1240.

［15］刘莎莎，顾煜炯，惠万馨，等.基于边界造波法的波浪数值模拟［J］.可再生能源，2013，31(2):100-103.

LIU Shasha，GU Yujiong，HUI Wanxin，et al.Wave numerical simulation based on wave-generation method of defining inlet boundary conditions［J］.Renewable Energy Resources，2013，31(2):100-103.