自适应GM⁃PHD滤波器在多目标追踪的应用

苍岩，陈迪，毕晓君

（哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001）

自适应GM⁃PHD滤波器在多目标追踪的应用

苍岩，陈迪，毕晓君

（哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001）

针对PHD滤波器中先验概率初始化时，新生目标出现的位置不确定，且目标强度计算区域必须为整个监测区域，造成算法低效率等问题，将原始算法通过PHD滤波的扩展项在预测步骤与更新步骤对新生目标与存活目标进行区分，再通过每一次扫描得到的量测自适应更新得到目标新生强度，依据量测的驱动来避免对先验概率初始化假设的问题。利用OSPA函数作为算法性能监测标准，利用仿真数据和实测数据对改进的算法进行了验证。结果显示，利用量测来驱动新生目标强度函数，对新生目标与存活目标先进性判断，目标数目估计正确率达到97%，OSPA距离较GM⁃PHD算法下降50%。

概率密度函数；高斯滤波器；多目标；跟踪算法；自适应估计

多目标跟踪技术已经发展了50多年，相继在防卫系统、监视系统等领域得到了广泛应用。该技术可分为传统多目标跟踪方法和新兴的多目标跟踪方法。新兴算法是一种基于随机有限集的概率假设密度滤波方法，其主要代表为粒子概率假设密度滤波［1］和高斯混合概率假设密度滤波［2］。通过将新生目标的概率密度函数设为均匀分布，可以提高近似高斯新生模型下的滤波性能，同时避免对高斯新生组件数目和位置参数的设置［3］；在利用量测驱动生成新生概率密度方面也有很多学者做了尝试，并将其应用到序贯蒙特卡洛概率假设密度滤波器中，减少新生目标的粒子数目，且能较准确地估计目标状态［5］；除了量测信息遗爱，利用似然信息来生成新生目标强度函数，能得到更好的跟踪效果［5］。本文基于上述文献的研究，将自适应新生目标概率密度函数应用到高斯混合框架下，从而提高目标跟踪精度和滤波器性能，并将原始算法和改进算法应用到海豚哨音信号追踪。

1 GM⁃PHD的改进

1.1 算法介绍

本算法引入基于量测的新生强度函数，该思想在文献［6⁃7］中被用于PHD粒子滤波实现的框架下。因高斯混合概率假设密度滤波无需聚类、粒子采样等步骤，在计算和状态估计方面比粒子滤波更具优势，然而在标准的高斯混合概率假设密度滤波器中，新生目标的强度函数被视为先验概率，该假设限制了实际工程中的应用，因此本文将该思想应用于高斯混合概率假设密度框架下进行实现，称为自适应高斯混合概率假设密度滤波器。该方法可通过每次扫描得到的量测值自适应地生成新生目标强度函数。

在PHD中，若将衍生目标忽略，预测方程可表达为

式中：〈g，f〉＝∫f（x）g（x）dx。状态向量x包含了两个部分，一部分是动力学的特征成分，如位置、速度，用s表示；另一部分是一个逻辑值，用l表示，用来区分新生目标和存活目标。l＝0代表存活目标，l＝1代表新生目标，于是状态向量x可表示为x＝（s，l）。这样新生目标强度函数可表示为

新生目标可以在下一时刻变为存活目标，但一个存活目标不能转变为新生目标，所以逻辑标记l仅能由1变为0，反之不成立。

转移密度函数为

其中

存活概率独立于l，因此

检测概率写为

则GM⁃PHD滤波预测方程式可被写为

将式（2）、（3）分别代入预测和更新方程，则预测方程可被重新写为

量测也不依赖于l，所以似然函数可表达为

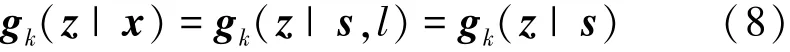
因此新的更新方程，对于新生目标与存活目标的显示表达分别为

1.2 算法步骤

改进算法将2种类型目标的预测和更新步骤分别计算，具体步骤如下：

步骤1：初始化

假设当k＝0时，新生目标和存活目标的初始强度函数分别为v0｜0（s，0）＝0和v0｜0（s，1）＝0。在k-1时刻，二者的强度函数分别表示为vk-1｜k-1（s，0）和vk-1｜k-1（s，1），并用高斯组件集

分别近似表示。所以k-1刻新生目标和存活目标强度函数的高斯形式可表示为

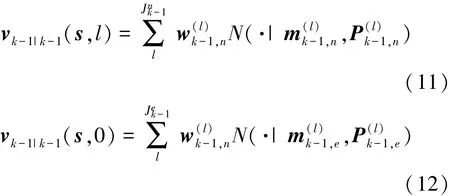
步骤2：联合

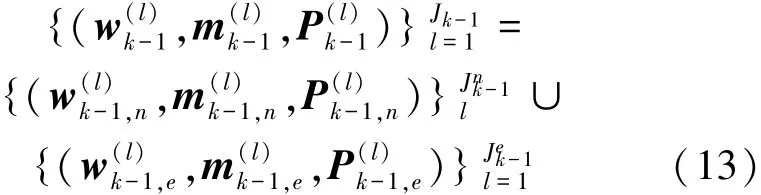
该集合代表了表达式vk-1｜k-1（s，0）+vk-1｜k-1（s，1）。

步骤3：预测

2种目标分别预测。

1）存活目标预测。

AGM⁃PHD滤波器拥有和GM⁃PHD滤波器相同的预测方程表达式：

值得注意的是，在k-1时刻，用来预测的高斯组件是步骤2中合并后的并集集合，这点不同于传统的GM⁃PHD滤波器。

存活目标的预测强度函数vk｜k-1（s，0）可用高斯形式表示：

2）新生目标预测。

中金公司的数据表明：以中美之间贸易量占全球的比例来看，中美之间集装箱贸易占全球4.7%，粮食贸易占全球7.8%，是占比最高的两个子类。从双方的依赖度而言，中国从美国进口占比高的主要为粮食（包括大豆），占中国粮食进口量的34.4%；美国从中国进口占比高的主要为集装箱，占美国集装箱进口量的37.4%。

对新生目标的数据处理不同于原始的方式，令量测方程为z＝h（）+q，其中h是个可逆函数，代表被检测到的目标状态矢量，q是量测噪声，且协方差为R。新生目标的信息可以通过当前量测集合得到，均值表示为＝h-1（zk，j），其中h-1函数式h的逆。协方差表示为＝HRHT，权值可用等式方程／Nnk计算得到，其中是k时刻对应的量测数目是预先设定的新生目标的数目。

步骤4：更新

1）存活目标更新。

更新方程表示为

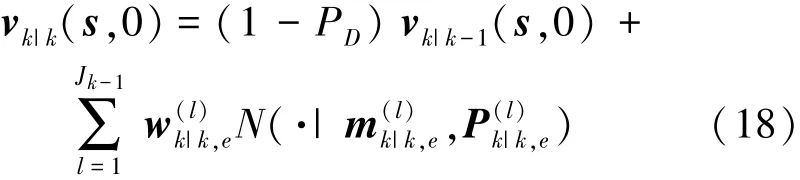
式中：ηk｜k-1，e、Sk｜k-1，e、Kk是更新高斯组件，与GM⁃PHD滤波器中的更新高斯组件相同。

2）新生目标更新。

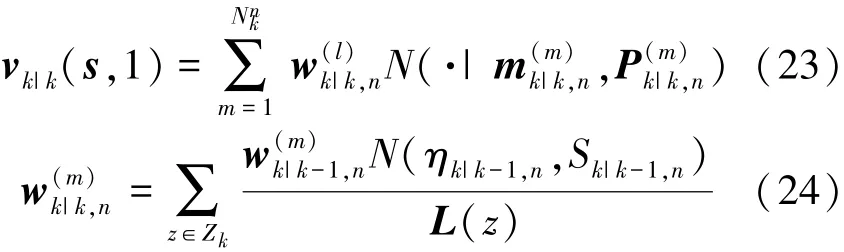
该算法的剩余部分与GM⁃PHD相同，此处不再重复讲述。

2 算法验证

2.1 仿真实验结果

本文给出了AGM⁃PHD算法和GM⁃PHD算法的对比仿真结果。在这个实验里，一共有4个目标，其中3个一直存在，另1个在第55 s生成。该仿真共运行100 s。每个目标k时刻的状态向量表示为。杂波随机有限集的强度函数为，其中u（·）在整个监视区域［-1 000，1 000］服从均匀分布。线性高斯模型为

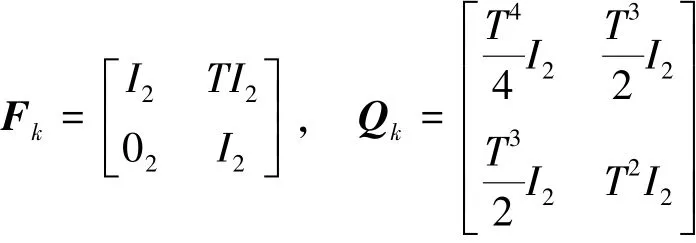
式中：T＝1 s是采样周期，σv＝2是过程噪声的标准方差，In、0n代表了n×n单位矩阵和零矩阵。存活概率和检测概率为Ps＝0.99和PD＝0.99，其他参数Tr＝10-5，U＝4，wTh＝0.5，Jmax＝100分别为剪枝阈值、合并阈值、权值阈值、高斯组件最大数。

图1 目标的真实轨迹Fig.1 The true targets trajectories

图1 表示具有目标的真实轨迹和具有杂波的量测，有3个目标一直存在，剩下的一个目标在55 s时生成；图2表示了GM⁃PHD和AGM⁃PHD的追踪性能，从估计的位置可以看出，AGM⁃PHD相对GM⁃PHD产生了较少的异常估计，具有更准确的跟踪性能。图3是由2种算法对真实目标追踪产生的估计目标数目，图4是2种算法的一个性能指标OS⁃PA［9］，OSPA是在点过程理论中被提出，其基于目标数目和位置的估计误差算出相应值，是用来衡量集合间差异程度的误差距离，其表达式如下

式中：参数p表示阶数，其值决定对异常值的敏感性；c代表截取距离，其决定了对于势误差的处罚程度，在该仿真实验中，分别设为1和100。该性能指标表明了算法在追踪目标准确性的好坏，可以看出，AGM⁃PHD的表现优于GM⁃PHD，且更稳定。

图2 GM⁃PHD和AGM⁃PHD估计性能对比Fig.2 The comparison of GM⁃PHD and AGM⁃PHD stimation

图3 估计数目对比Fig.3 Comparison of number of targets

图4 OSPA距离的对比Fig.4 Comparison of OSPA distance

2.2 海豚哨声信号追踪验证

2.2.1 海豚哨声信号的动态模型

海豚可以产生一系列哨音信号来表达特殊的信息，将不同的哨音信号视为不同的目标，所以对于哨音信号的追踪问题可当作多目标追踪的问题来处理。在哨音信号追踪时，其状态向量由频率f和调频斜率α［10］构成：xk＝［f，α］T。此时在多目标追踪中的线性高斯模型表示为其中vk是零均值高斯噪声，T是采样频率，对应的采样频率为fs＝1／T。在量测模型中，只有频率信息有用，量测方程表示为zk＝Hxk+wk，其中量测矩阵H为H＝10[]，wk是零均值高斯噪声，其协方差为Pw。状态转移密度fk｜k-1（x｜x'）服从N（xk；mfk｜k-1，Pfk｜k-1）分布，其中mfk｜k-1＝01×2，Pfk｜k-1＝为量测噪声的频率标准方差，是调频斜率噪声的标准方差。似然函数gk｜k-1（z｜x）服从N（x；mg，Pg），其中mg＝0，Pg＝Pw。

2.2.2 滤波器初始化

哨音信号频率的初始数目是一个随机值，高斯组件的均值在2～30 kHz范围内均匀分布，因为大部分哨音基频的范围是2～30 kHz。每个高斯组件的协方差矩阵是

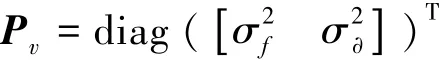
式中：σf和σ∂一般设为10和100。合并阈值U＝4，剪枝阈值Tr＝1×10-5，采样周期T＝1 s，权值阈值wTh＝0.5和最大允许高斯组件数Jmax＝100。

2.2.3 数据实验结果

在该实验中，将GM⁃PHD和AGM⁃PHD滤波器用于短喙真海豚和条纹原海豚的哨音追踪中，杂波强度函数Kk是常数。γ均匀分布在0～25 kHz范围内，因此扫描杂波平均数目值γ设为5。调协频率概率分布，频率初始频率概率分布，存活概率Ps＝0.99，检测概率PD＝0.95，新生目标强度函数设定为κ＝5／25 000。

图5是分别利用AGM⁃PHD和GM⁃PHD算法对短喙真海豚哨音信号进行追踪。图6是分别利用AGM⁃PHD和GM⁃PHD算法对条纹原海豚哨音信号进行追踪，实验数据被延长到了500次扫描。从图中可以看出AGM⁃PHD滤波算法不仅可以有效地抑制杂波，还可以得到较完整的目标轨迹，而GM⁃PHD的抑制杂波的能力仍不如前者，且对于目标轨迹的追踪出现漏追现象，得到的目标轨迹较稀疏。AGM⁃PHD在抑制大量杂波的同时，亦得到了清晰的跟踪轨迹。

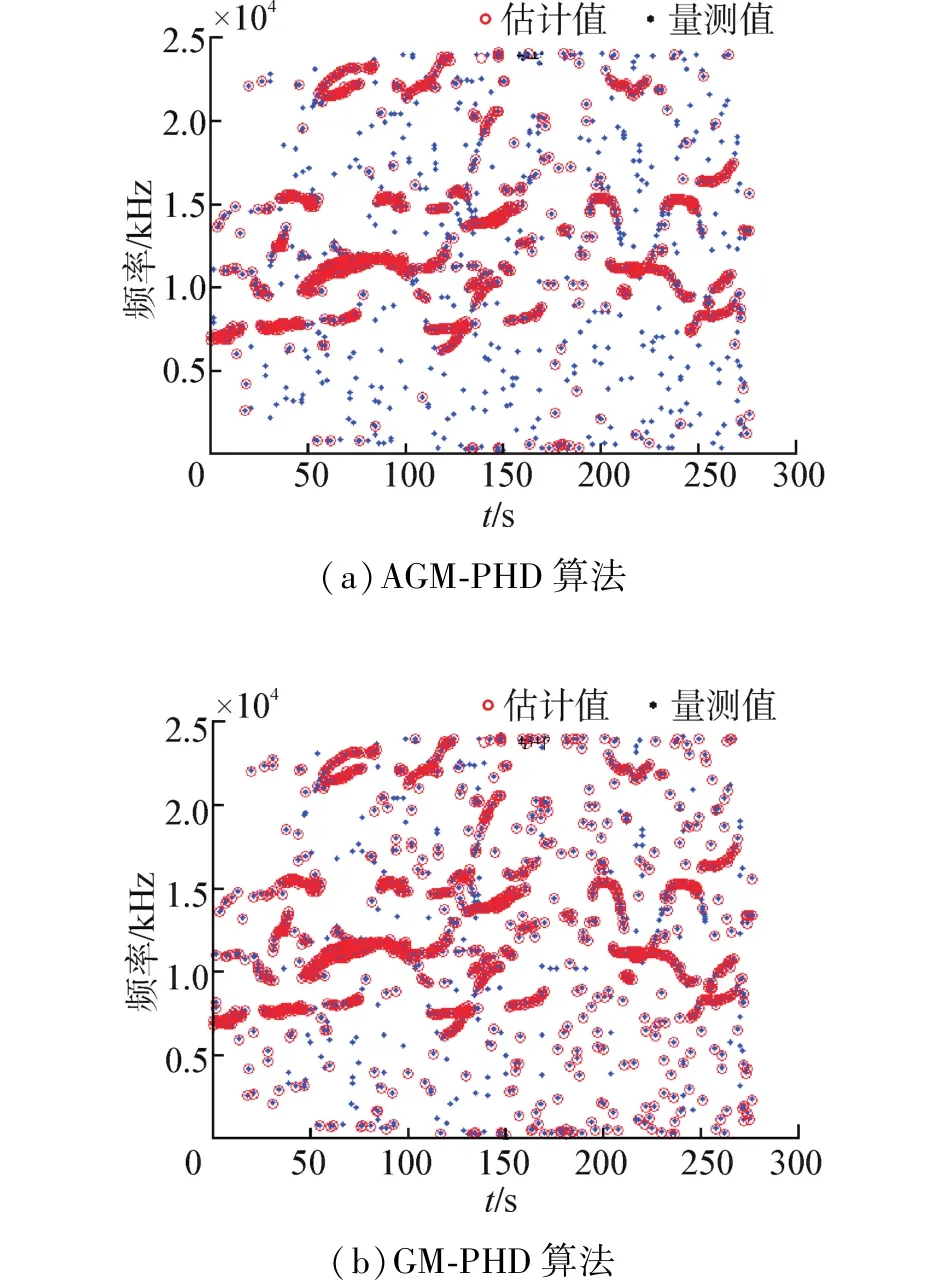
图5 对短喙真海豚哨音信号追踪Fig.5 Estimated whistle tracks for delphinus dolphins

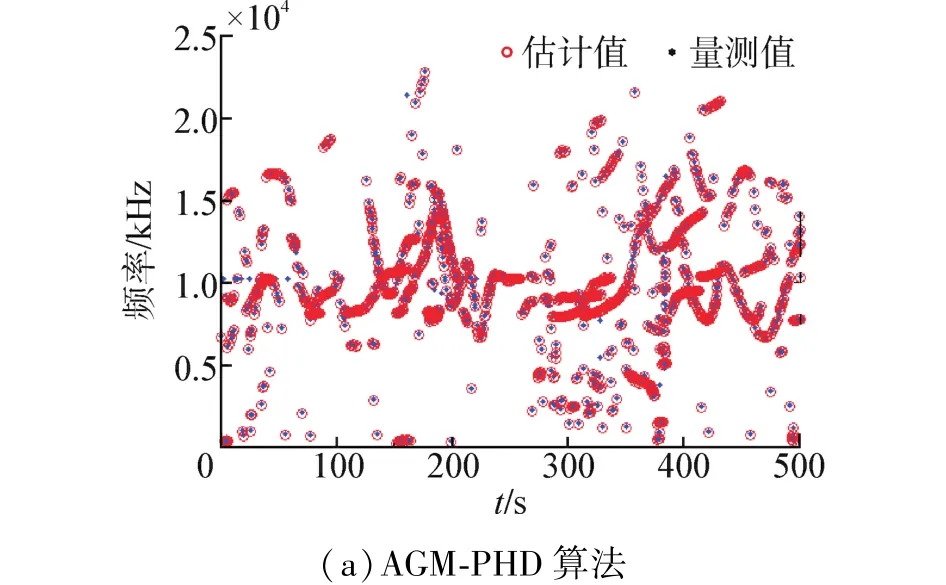
图6 对条纹原海豚哨音信号追踪Fig.6 Estimated whistle tracks for stenella coeruleolba

3 结论

因传统的PHD滤波器将新生目标强度函数设为已知，造成程序运算效率低，且不适用于实际应用，本文提出了自适应高斯混合概率假设密度（AGM⁃PHD）滤波算法来解决该问题，文中介绍了该算法的实现步骤，最后通过仿真，将改进算法与原始算法进行对比来验证其跟踪性能。得到如下结论：

1）该算法可以利用量测来驱动新生目标强度函数，因此相对原始高斯混合概率假设密度滤波算法能够更为准确地估计目标数目，其估计误差减小，此外，改进算法对新生目标与存活目标先进行判断，再进行相应步骤的预测与更新，从而减少程序的运行时间也计算复杂度。

2）本文对2种海豚的哨音进行追踪，两组实验利用了相同的方法与参数，尽管哨音信号的波形不同，杂波数不同，但得到的实验结果类似。对比结果可知，AGM⁃PHD滤波算法相对于原始算法在抑制杂波方面与对哨音信号的跟踪效果方面均优于GM⁃PHD滤波算法，该实验结果证明了AGM⁃PHD滤波算法跟踪性能的有效性。综上，即使当有大量的噪声存在以及信号分量之间存在着彼此交叉时，AGM⁃PHD算法在追踪精度和准确性方面仍然优于GM⁃PHD算法。

［1］戴丁樟.粒子滤波算法研究及其在目标跟踪中的应用［D］.哈尔滨：哈尔滨工业大学，2006：1⁃67.DAI Dingzhang.Research of particle filter and its application in target tracking［D］.Harbin：Harbin Institute of Technolo⁃gy，2006：1⁃67.

［2］VO B N，MA W K.The Gaussian mixture probability hy⁃pothesis density filter［J］.IEEE Transactions on Signal Pro⁃cessing，2006，54（11）：4091⁃4104.

［3］BEARD M，VO B T，VO B N，et al.A partially uniform target birth model for gaussian mixture PHD／CPHD filtering［J］.IEEE Transactions on Aerospace and Electronic Sys⁃tems，2013，49（4）：2835⁃2844.

［4］RISTIC B，CLARK D，VO B N.Improved SMC implementa⁃tion of the PHD filter［C］／／Proceedings of the 13th Interna⁃tional Conference on Information Fusion.Edinburgh：IEEE，2010：1⁃8.

［5］RISTIC B，CLARK D，VO B N，et al.Adaptive target birth intensity for PHD and CPHD filters［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48（2）：1656⁃1668.

［6］ERDINC O，WILLETT P，BAR⁃SHALOM Y.Probability hypothesis density filter for multitarget multisensor tracking［C］／／Proceedings of the 8th International Conference on Information Fusion.Philadelphia：IEEE，2005：1.

［7］朱孟凯.基于随机集理论的多目标跟踪算法研究［D］.长春：吉林大学，2013：1⁃66. ZHU Mengkai.Research of multi⁃targets tracking algorithm based on random set theory［D］.Changchun：Jilin Universi⁃ty，2013：1⁃66.

［8］TOBIAS M，LANTERMAN A D.Techniques for birth⁃parti⁃cle placement in the probability hypothesis density particle filter applied to passive radar［J］.IET Radar，Sonar＆Navi⁃gation，2008，2（5）：351⁃365.

［9］HOFFMAN J，MAHLER R P S.Multitarget miss distance via optimal assignment［J］.IEEE Transactions on Systems，Man and Cybernetics，Part A：Systems and Humans，2004，34（3）：327⁃336.

［10］AHMED I.Multiple track estimation using Gaussian mix⁃ture probability hypothesis density filter［J］.IOSA Journals of VLSI and Signal Processing，2013，2（4）：37⁃42.

Application of adaptive GM⁃PHD filters to multi⁃target tracking

CANG Yan，CHEN Di，BI Xiaojun

（College of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China）

The problem is that when initializing prior probability in a probability hypothesis density（PHD）filter，the position of newborn targets is indefinite，and the targeting computations must search the whole monitoring do⁃main，noticably decreasing efficiency.This paper expands on the original PHD filter，to adaptively distinguish new⁃born targets from surviving targets in the prediction and updating steps.It then measures again，updating newborn target strength after each scan，thus avoiding the problem of prior probability parameter initialization.The optimal sub pattern assignment（OSPA）function was used to benchmark the performance of the algorithm，plus both simu⁃lated and tested data were used for validation.Using such measurements greatly enhances discrimination between newborn targets and surviving targets.The results show that estimation accuracy for the number of targets has in⁃creased to 97%，while the OSPA distance has decreased 50%than the original GM⁃PHD algorithm.

probability density function；Gaussian filter；multiple targets；tracking algorithm；adaptive estimation

10.11990／jheu.201409014

TN911.7

：A

：1006⁃7043（2015）11⁃1526⁃06

http：／／www.cnki.net／kcms／detail／23.1390.u.20151109.1526.002.html

2014⁃09⁃04.网络出版日期：2015⁃11⁃09.

国家自然科学基金资助项目（61175126，61371175）；中央高校基本科研业务费专项资金资助项目（HEUCFZ1209）；教育部博士点基金资助项目（20112304110009）.

苍岩（1978⁃），女，讲师，博士；毕晓君（1964⁃），女，教授，博士生导师.

苍岩，E⁃mail：cangyan＠hrbeu.edu.cn.