电子碰撞激发氢原子和氦离子散射微分截面的计算

赖卓劲，陈德锋，潘霖庆，蒋晓涵，徐永亮，陈长进

(汕头大学理学院，汕头 515063)

电子碰撞激发氢原子和氦离子散射微分截面的计算

赖卓劲，陈德锋，潘霖庆，蒋晓涵，徐永亮，陈长进

(汕头大学理学院，汕头 515063)

本文详细介绍计算电子碰撞激发散射截面的扭曲波玻恩近似(DWBA)理论模型，并对低能DWBA模型进行修正.利用修正的DWBA模型计算了电子碰撞激发氢原子和氦离子1s-2s 和1s-2p的散射微分截面.将关于氢原子由基态到n=2态的电子碰撞激发散射微分截面与绝对实验测量数据比较，发现二者符合得很好，这验证了我们对DWBA修正的正确性.本文工作为拟合强场诱导的氦原子非序列双电离关联电子动量谱提供了有效的理论方法.

电子碰撞激发; 散射微分截面; 扭曲波玻恩近似

1 Introduction

The process of electron impact excitation of atoms and ions is one of the most basic and important processes in atomic physics. Theoretical investigations of such problems are of not only practical interest but also more fundamental interest. Numerous theoretical methods have been proposed for calculations of differential cross sections (DCSs) for electron impact excitation, including the distorted wave Born approximation (DWBA)[1,2], the second-order distorted wave model[3], the convergent close-coupling (CCC) calculations[4], and theR-matrix method[5], among which the DWBA is the simplest. The sophisticated theoretical models, such as the CCC and theR-matrix method, are supposed to be able to reproduce accurate DCS in angular distribution and absolute magnitude as well at low incident energies. On the other hand, for high energies, both the total cross sections (TCSs) and the DCSs predicted by DWBA are in fairly good agreement with the absolute measurements. However, it has been well recognized that, at low energies, the TCS predicted by the DWBA substantially overestimates the experimental values. "Ideally, one could use theR-matrix approach for low energies, the DWBA for high energies, and the two theories would yield the same results for intermediate energies. Unfortunately, we do not live in an ideal world."[6]

The purpose of this work is to calibrate the DWBA for electron impact excitation of H and He+at low energies by employing the empirical formula proposed by Tongetal.[7]. This calibration procedure has been previously applied to correct the overestimate of DWBA on the DCS for electron impact excitation of Ne and Ar[8].

Our ultimate objective is to apply the calibrated DWBA to simulate the correlated momentum distributions in nonsequential double ionization (NSDI) of He in strong laser fields[9,10].

The process of NSDI is one of the laser-induced rescattering processes, which still remains one of the most interesting and challenging topics in strong field physics. Both electron impact ionization and electron impact excitation of ions could be involved in NSDI. In the last two decades a lot of experimental measurements have been performed, particularly noteworthy are the correlated momentum distributions of the two outgoing electrons which were measured at the turn of this century[11]. In the meantime, a number of theoretical efforts have been devoted to this problem as well. In one of the theoretical models, which was developed by Chenetal.[12,13], the correlated two-electron momentum spectra can be treated as a product of the wave packet for laser-induced returning electrons and the differential cross sections for the laser-free electron impact excitation and/or ionization of the parent ion. In the practical simulations of the correlated electron momentum distributions for NSDI, one needs to evaluate the DCS for electron impact excitation of the parent ion to all possible excited states at all incident energies from threshold to the maximum returning electron energy which is usually less than 200 eV. Due to the heavy computational demand, relatively simple and efficient theoretical approaches are highly desired. Since the shape of the DCS predicted by DWBA is typically in fairly good agreement with the experimental measurements, once the overestimate of DWBA on the DCS is corrected, the calibrated DWBA can serve as a good candidate for such required theoretical tools.

The organization of this paper is as follows: In section 2, the theory of DWBA for electron impact excitation is presented in detail and the method to calibrate DWBA is proposed. In section 3, the normalization factors for DWBA at incident energies below 1000 eV are given for electron impact excitation of H and He+from 1s to 2s and 2p, and the calibrated DCSs of DWBA for H at 50 eV and 100 eV are compared with the experimental measurements. Furthermore, some calibrated DCSs of DWBA for H and He+at four different incident energies below 100 eV are analyzed. And finally some conclusions are drawn in section 4.

Atomic units are used in this paper unless otherwise specified.

2 Theory

In this section, we present the general form for DWBA theory in detail on electron impact excitation of atoms which can be easily applied to electron impact excitation of ions. A method used to calibrate the DWBA at energies below 1000 eV is also given.

2.1 Basic equations

The problem to be considered here is inelastic electron-atom (e-A) scattering. The Hamiltonian for such a process is given by

(1)

wherer1andr2are the position vectors for the projectile and the bound state electron with respect to the nucleus, respectively. In Eq. (1),VA+is the effective potential based on single active electron approximation, which takes the form as

(2)

where the parametersai, as given explicitly in Table 1 in Tong and Lin[14], were obtained by fitting the calculated binding energies of the ground state and the first few excited states of the target atom using this potential to the experimental data. Both the exact initial state wave functionΨi(r1,r2) and the final state wave functionΨf(r1,r2) of the system satisfy the Schrödinger equation

HΨj(r1,r2)=EΨj(r1,r2) (j=i,f),

(3)

whereEis the total energy.

Since Eq. (3) cannot be solved analytically, one has to employ approximate Hamiltonians, which can be expressed as

+VA+(r2) (j=i,f),

(4)

whereUi(Uf) is the distorting potential used to calculate the wave functionχki(χkf) for the projectile in the incident (exit) channel with momentum ki(kf). With this approximation, the initial (final) state wave function can be expressed as a product of the initial (final) state wave function for the projectile and the wave function for the bound electron in the ground (excited) state.

The initial and final state wave functions for the projectile satisfy the differential equation

(5)

and the bound state wave functions are eigenfunctions of the equation

(6)

whereεj(j=i,f) are the corresponding eigenenergies of the initial and final states. Due to energy conservation,

εf.

(7)

In the distorted wave Born approximation, the direct transition amplitude for excitation from an initial stateΦito a final stateΦfis given by

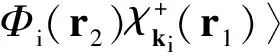
(8)

whereViis the perturbation interaction,

(9)

And the exchange scattering amplitude is given by

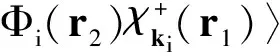
(10)

2.2 Partial wave expansions

To evaluate the scattering amplitude, we perform standard partial wave expansions. The distorted wave for the incident electron with outgoing (+) boundary condition is expanded as

(11)

(12)

In this work, all continuum waves are normalized toδ(k-k′). For a plane wave, the radial componentχl(k,r)/krin Eqs. (11) and (12) is a standard spherical Bessel functionjl(kr) .

The initial and final bound states can be expressed as

, f ).

(13)

Inthescatteringamplitude(8),theperturbationpotentialisthelastremainingquantitywhichneedstobeexpanded.Thefirsttermintheperturbationpotential(9)canbeexpandedas

(14)

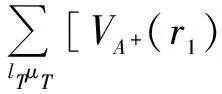
(15)

Theexpansions(14)and(15)thenyield

(16)

wheretheradialfactorAlT(r1,r2) is given by

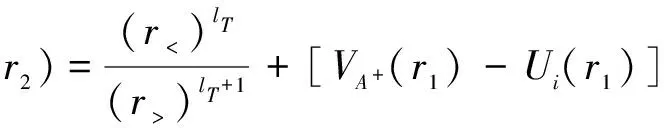
(17)

2.3Calculationofthedifferentialcrosssections

Thedifferentialcrosssectionforelectronimpactexcitationofatomsisgivenby

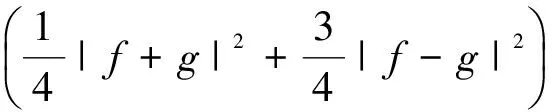
(18)

wheretheprefactorNdenotes the number of electrons in the subshell from which one electron is excited.

With the expansions given in the above subsection, the direct scattering amplitude is given by

×

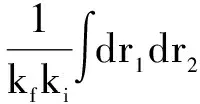
AlT(r1,r2)φNiLi(r2)χli(ki,r1)×F1F2

(19)

whereF1andF2are given by

(20)

and

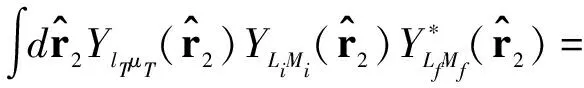
(21)

ToperformtheintegralsoverpolaranglesinEqs. (20)and(21),wehaveusedtherelations

(22)

and

(23)

whereC(l1l2l3;m1m2m3) is a Clebsch-Gordan coefficient.

The product ofF1andF2can be further simplified as

;000)C(lTLiLf;000)×

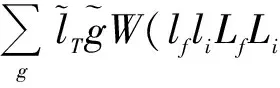
C(lfgLf;μfμgMf),

(24)

whereW(l1l2l3l4;l5l6) is a Racah coefficient, and we have used

C(l1l2l3;m1m2m3)C(l3l4l5;m3m4m5)=

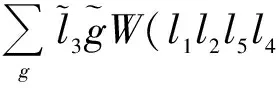
C(l1gl5;m1μgm5).

(25)

Furthermore,byusing

C(l1l2l3;m1m2m3)=

(26)

wecanrewriteC(lfgLf;μfμgMf) in Eq. (24) as

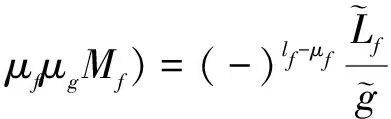
C(lfLfg;μf,-Mf,-μg).

(27)

Consequently,

;000)C(lTLiLf;000)

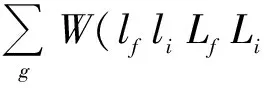
×C(lfLfg;μf,-Mf,μf-Mf)δμi+Mi,Mf-μf.

(28)

SubstitutingEq. (28)intoEq. (19),wefinallyobtain

;μi,Mi,μi+

Mi)×C(lfLfg;μf,-Mf,μf-Mf)C(lflilT;000)

AlT(r1,r2)φNiLi(r2)χli(ki,r1).

(29)

Similarly,theexchangescatteringamplitudeisgivenby

C(liLig;μi,Mi,μi+Mi)×C(Lflfg;-Mf,-μf,-Mf-μf)C(LflilT;000)C(lTLilf;000)×W(LflilfLi;lTg)

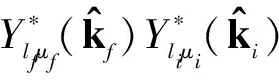
χlf(kf,r2)AlT(r1,r2)φNiLi(r2)χli(ki,r1).

(30)

2.4Distortingpotentials

IntheDWBAmodel,thedistortingpotentialsUiandUfwhich are used in Eq. (5) to evaluate the wave functions for the projectile in the initial and final states respectively play an important role in the numerical calculations, since the calculated DCSs are sensitive to the distorted wave functions describing the projectile. Unfortunately, neitherUinorUfis determined directly by the formalism. Here, we use static potentials which take the form as

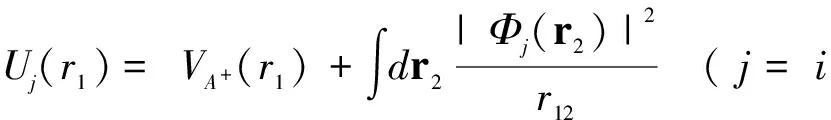
(31)

Asshownpreviously,VA+(r) in Eq. (31) is the atomic potential used to evaluate eigenstate wave functionsΦiandΦffor the bound electron in the initial and final states, respectively. Obviously, the distorting potentials given by Eq.(31) for electron impact excitation of atoms are neutral asymptotically.

2.5 Calibration of DWBA

To evaluate the total cross sections for electron impact excitation, Tongetal.[7]employed an empirical formula

(32)

where

(33)

with △Eis the excitation energy for a given transition andεis the eigenenergy of the corresponding excited state in atomic hydrogen. The parametersβ,γandδin Eq. (33) have been obtained initially by fitting the TCS to the convergent-close coupling (CCC) results for hydrogen from 1s to 2p and further tested fore+He+(1s) →e+He+(2p). However, it has been found that, with the parameters given in Ref. [7], the formula Eq. (32) fails to predict the correct values of the TCS for excitation of other atoms and ions. Even for H and He+, the TCS for excitation to other excited states reproduced by Eq. (32) are much higher than the CCC data and the shape of the TCS as a function of incident energy does not agree with the CCC very well, either.

To adjust the overall difference in magnitude, we introduce a prefactor to modify the empirical formula, which is given by

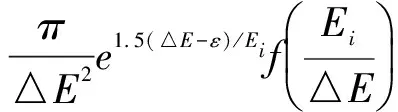
(34)

Itshouldbenotedthat,inEq. (34),εdenotes the eigenenergy of the corresponding excited state in target atoms or ions. In the present work, we apply the same fitting procedure as in Ref. [7] to obtain the parameters. For excitations of H and He+from 1s to 2s, the parameters we obtained areβ= 0.7638,γ= 1.1759, andδ= 0.6706, which are different from those in Ref. [7]. It has been found that with this set of parameters, the TCS reproduced by Eq. (34) are in better agreement with CCC in shape. These parameters are further tested by comparing the predicted excitation cross section with CCC for excitations of H and He+from 1s to 3s and 4s. For excitations of H and He+from 1s tonp (n=2, 3 and 4), the parameters areβ= 1.32,γ= -1.08, andδ= -0.04. The prefactor α is then determined by matching the TCS from Eq. (34) with the CCC data at high energies.

It should also be noted that the TCS of CCC are not available for most atoms or ions. Hence, the applicability of the above fitting procedure to excitation of other atoms and ions is quite limited. Fortunately, both the DCS and the TCS of DWBA are reliable at high energies. Therefore, the prefactorαcan be obtained by matching the TCS from Eq. (34) with the DWBA results at high energies, say 1000 eV, provided that the parametersβ,γand δ remain the same for all target atoms and ions.

(35)

TocalibratetheDWBAatlowenergies,wedefineanormalizationfactor

C(Ei)=σM-Tong(Ei)/σDWBA(Ei).

(36)

BymultiplyingtheDCSofDWBAbythenormalizationfactorateachincidentenergy,oneobtainsthecalibratedDWBAas

.

(37)

3 Results and discussion

ToobtainthenormalizationfactorstocalibratetheDCSofDWBA,wecalculatetheTCSfromtheempiricalformulaofEq. (34)andtheTCSofDWBA.TheresultsareshowninFigs. 1and2forexcitationsofHandHe+,respectively.ThecorrespondingCCCresults[15]arealsoplottedforcomparison.ItcanbeseenthattheCCCdataforexcitationfrom1sto2sarereproducedverywellforbothHandHe+whileforexcitationfrom1sto2pslightdifferencesexist.Whereas,theagreementbetweentheTCSofTongandCCCcanbeimprovediftheTCSofTongat1000eVisfittedtoCCCratherthanDWBA.ThereasonthatwefittheTCSofTongat1000eVtoDWBAinsteadofCCCisthatDWBAresultsarealwaysavailable.

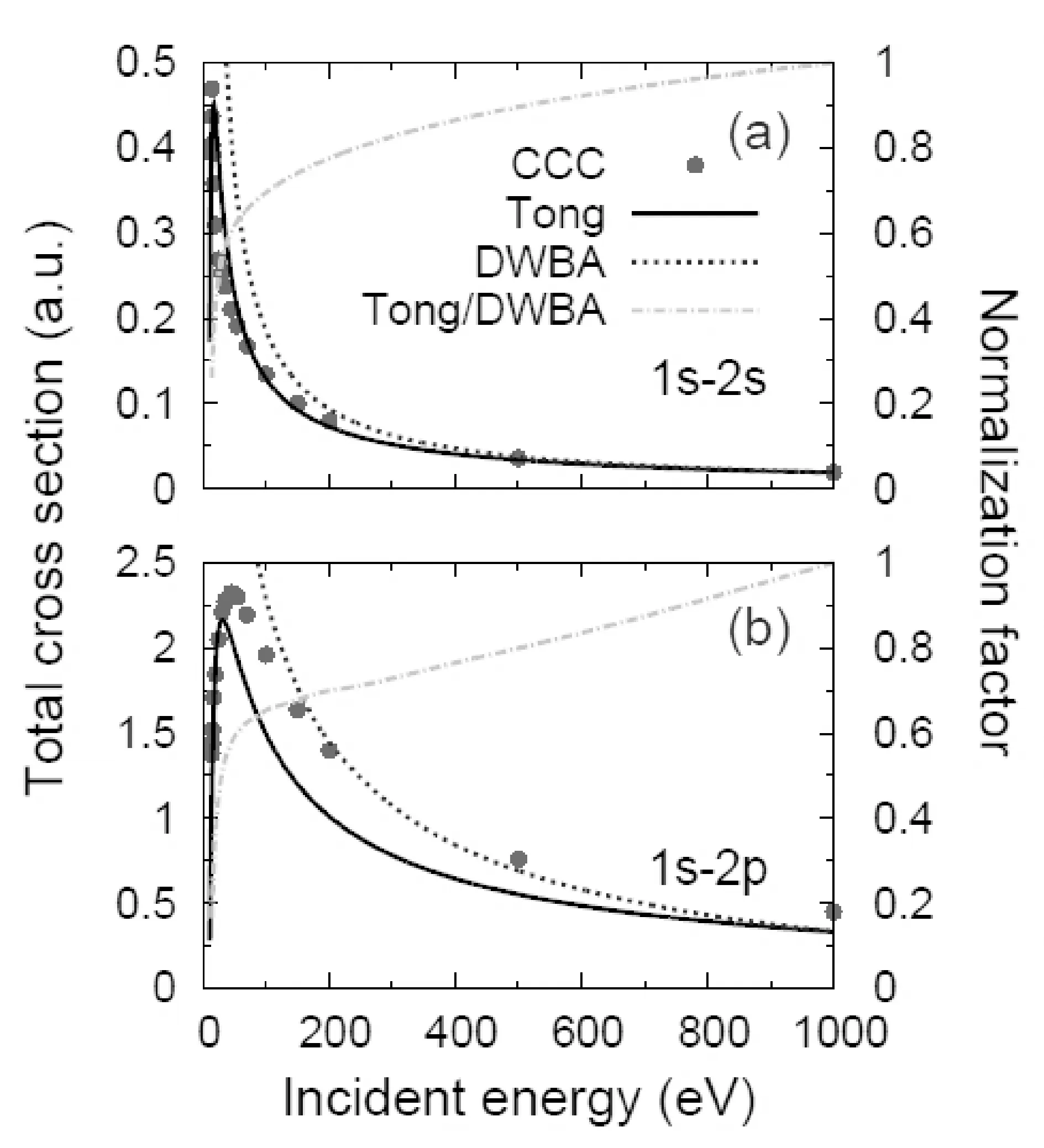
Fig.1 TCSs (left vertical axis) and normalization factors of DWBA (right vertical axis) for excitation of H from (a) 1s to 2s and (b) 1s to 2p at incident energies from the excitation energy of 10.2 eV to 1000 eV. Dotted curve, total cross sections of DWBA; Solid curve, total cross sections calculated using the empirical formula Eq. (34); Chain curve, normalization factor given by Tong/DWBA; Solid circles, CCC data[15]

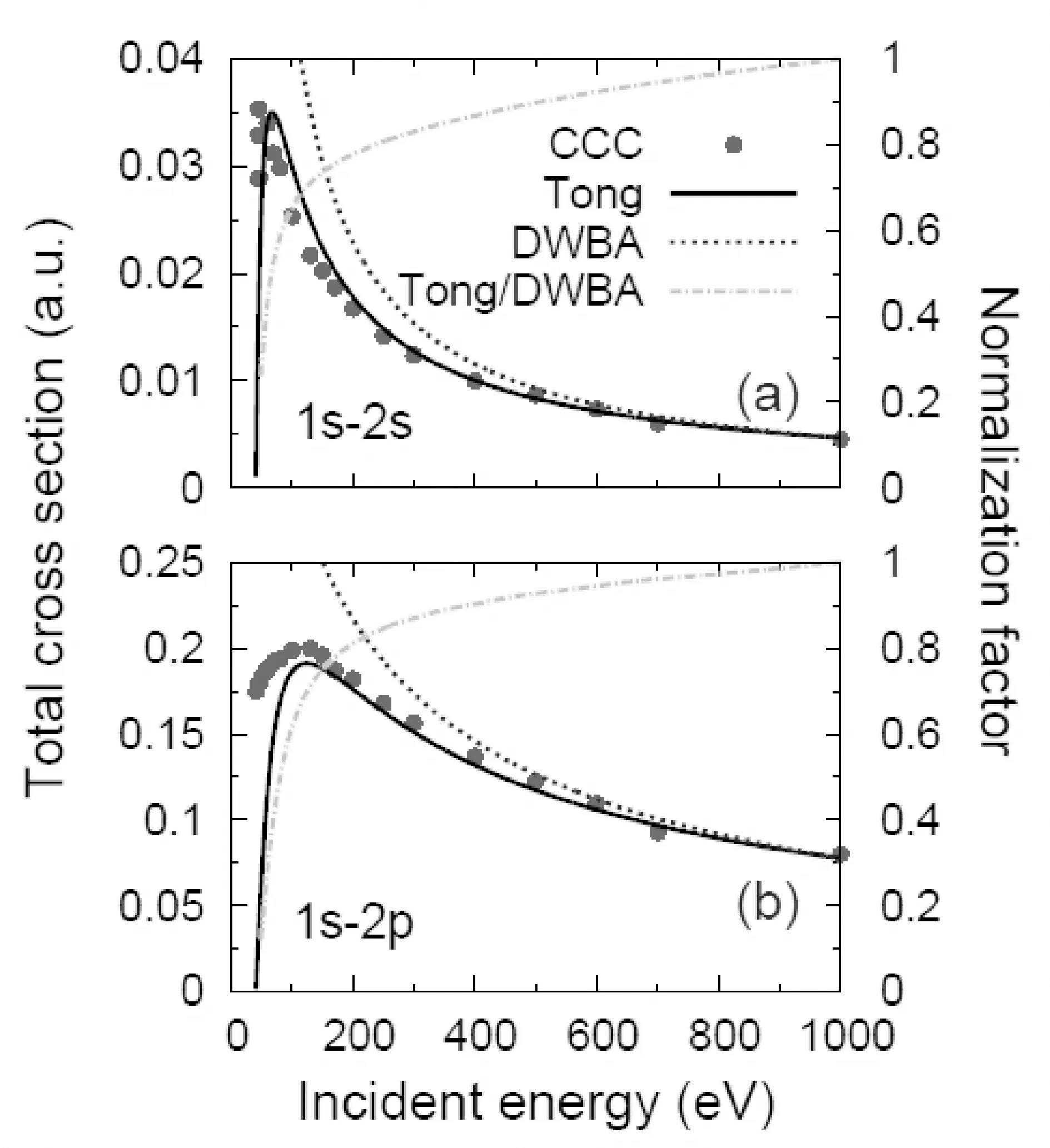
Fig.2 TCSs (left vertical axis) and normalization factors of DWBA (right vertical axis) for excitation of He+ from (a) 1s to 2s and (b) 1s to 2p at incident energies from the excitation energy of 40.8 eV to 1000 eV. Dotted curve, total cross sections of DWBA; Solid curve, total cross sections calculated using the empirical formula of Eq. (34); Chain curve, normalization factor given by Tong/DWBA; Solid circles, CCC data[15]

TheabsoluteexperimentalmeasurementsofKhakooet al.[16]forelectronimpactexcitationofthe12S → 22S + 22PlevelsofHatincidentenergiesof50and100eVprovidetheexcellentpossibilityofastringenttestforthepresentcalibrationprocedure.ItisillustratedinFig. 3thatthecalibratedDWBADCSsfollowtheexperimentaldataverywelloverthewholeangularregionforbothincidentenergies.Toseethecontributionsfromtheexcitationsof12S → 22Sand12S → 22Pseparately,thecorrespondingtheoreticalDCSsofthecalibratedDWBAarealsoplottedinFig. 3forcomparison.Onecanseethattheexcitationof1sto2pdominatestheforwardscatteringforangularregionfrom0oto45oat50eVand0oto30oat100eV.Ontheotherhand,theexcitationof1sto2scannotbeneglectedintheregionoflargerscatteringangles.

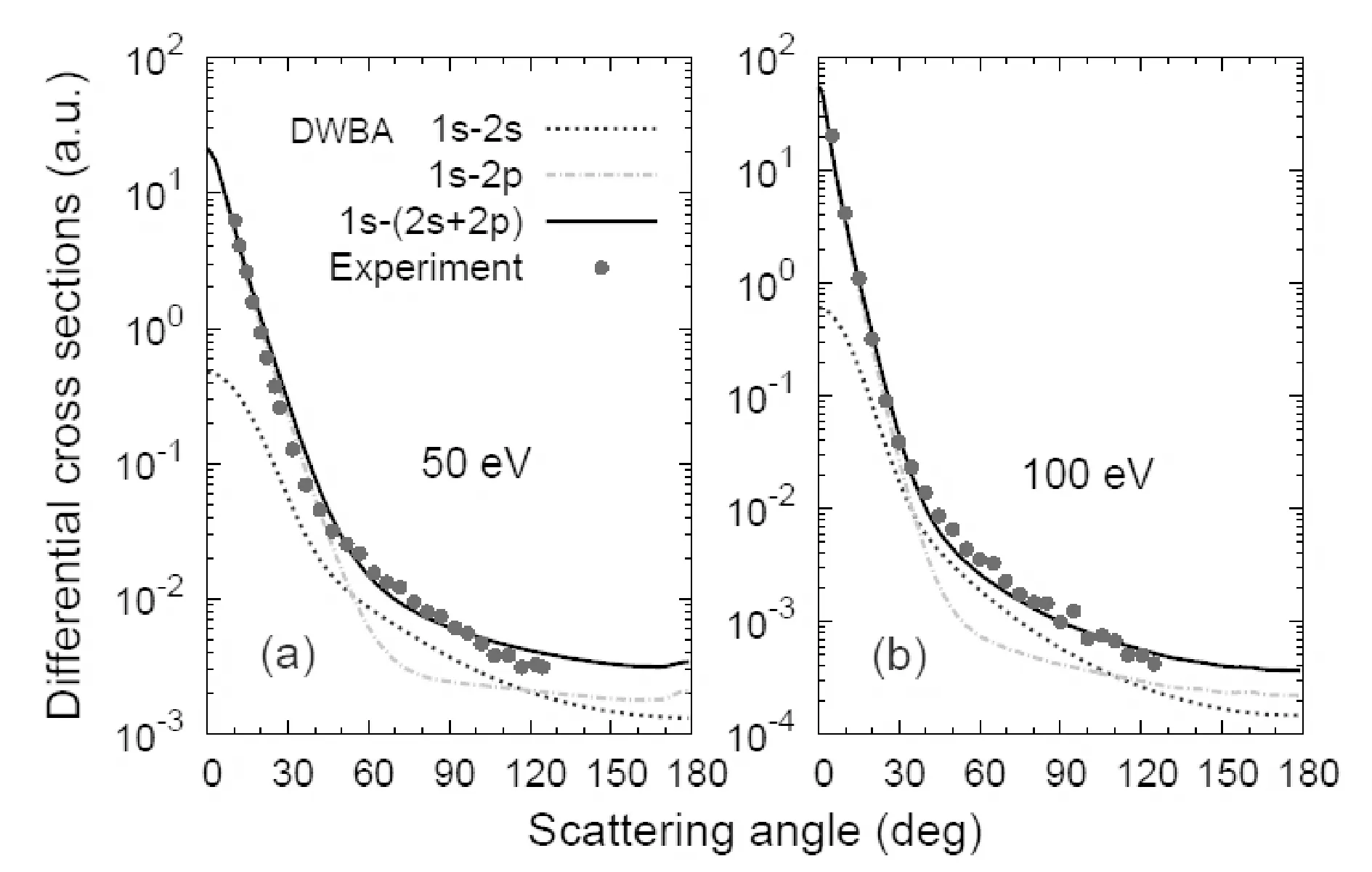
Fig.3 Comparison of the DCSs of the calibrated DWBA with experimental measurements of Khakoo et al.[16] for excitation of H from ground state to n=2 state at incident energies of (a) 50 eV and (b) 100 eV

InFig. 4weshowtheDCSsofDWBAweightedbythenormalizationfactorsforexcitationsofHfrom1sto2sand1sto2patincidentenergiesof15, 25, 50and100eV,respectively.TheslopesofDCSsforbothexcitationsof1sto2sand1sto2pchangemorerapidlyatlargerscatteringanglesasincidentenergydecreases.Inadditiontotheslopechange,extraminimaarereproducedbytheDWBAaround70oforexcitationof1sto2pand100ofor1sto2pat15eV.

Fig.4 Calibrated DCSs of DWBA for excitation of H from (a) 1s to 2s and (b) 1s to 2p at incident energies of 15, 25, 50, and 100 eV, respectively

Fig. 5showsthesimilarresultsforexcitationsofHe+atenergiesbelow100eV.ComparedtotheexcitationofH,enhancedbackwardscatteringDCSsarepredictedbytheDWBAduetolargerCoulombattractiontothescatteredelectronsincelargeanglescatteringtakesplacewhentheprojectileisclosertothenuclearofHesuchthatitseesmorechargethanthenuclearchargeofH.Asaresult,aminimumappearsintheDCSsforbothexcitationof1sto2sand1sto2pat45and60eV.BothofthedepthsandpositionsoftheminimuminDCSshavesignificantphysicalimportancesincetheyreflectthestructureinformationofthetargets.Inaddition,withtheincreaseofincidentenergy,theangleatwhichtheslopechangesdoesnotmoveasmuchasthatforH,whichevenalmostremainsfixedat110ofortheexcitationofHe+from1sto2p,asshowninFig. 5(b).

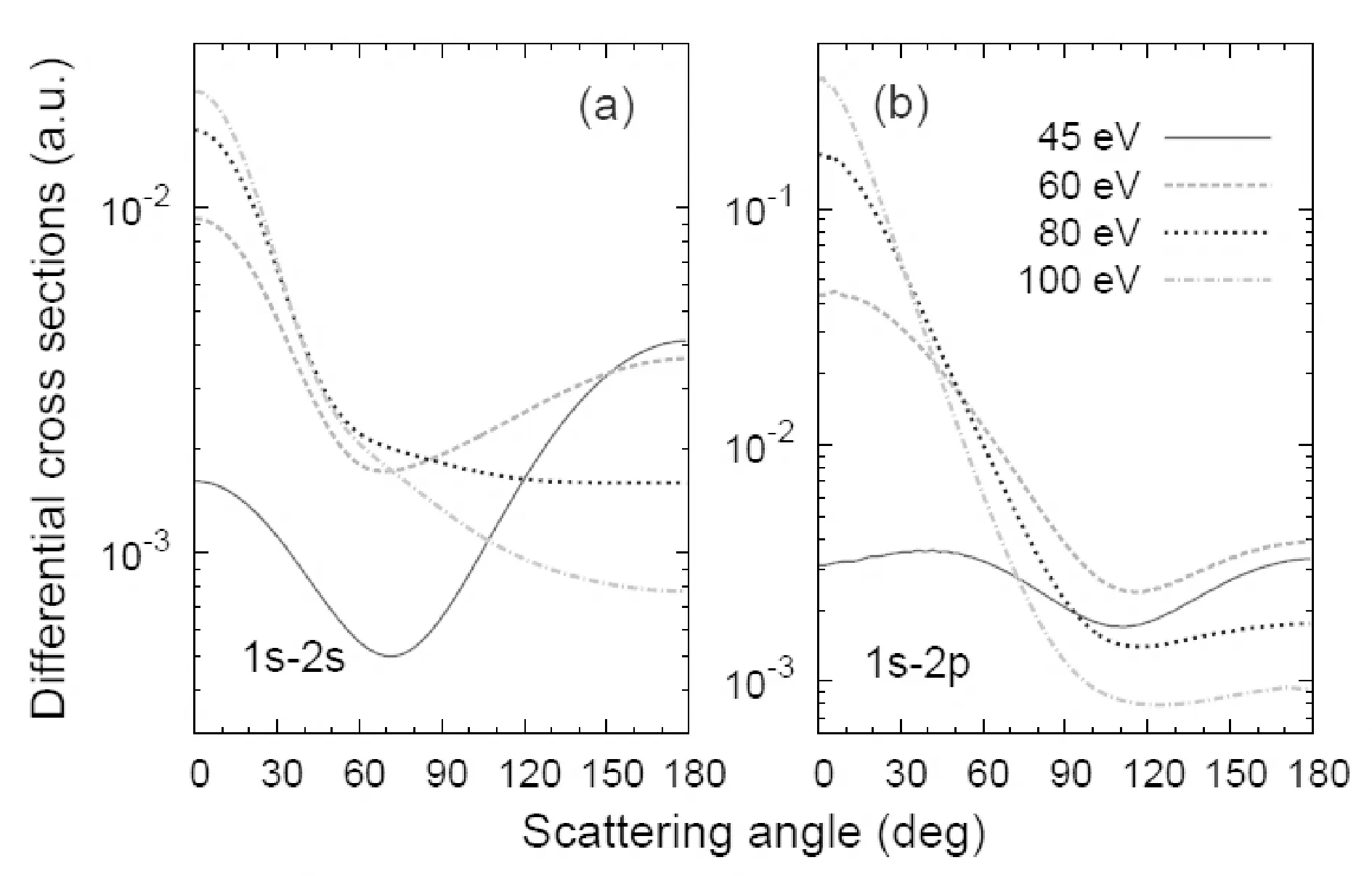
Fig.5 Calibrated DCSs of DWBA for excitation of He+ from (a) 1s to 2s and (b) 1s to 2p at incident energies of 45, 60, 80, and 100 eV, respectively

4 Conclusions

WepresentamethodtocorrecttheoverestimateofDWBAontheTCSsforelectronimpactexcitationofHandHe+.ThepurposeofthisworkistoapplythecalibratedDWBAtosimulatethecorrelatedmomentumdistributionsforlaser-inducednonsequentialdoubleionizationofHe.Thecalibrationmethodisbasedontwoassumptions: (1)therelativeangulardistributionsoftheDCSspredictedbytheDWBAatlowincidentenergiesarefairlyaccurate,and(2)theTCSsreproducedbytheDWBAathighincidentenergiesarereliable.ThevalidityofthecalibrationmethodisconfirmedbytheagreementbetweentheDCSsobtainedbythecalibratedDWBAandtheabsoluteexperimentalmeasurementsforexcitationsofHfromthegroundstateton=2state.ThecalculatedDCSswiththecalibratedDWBAforexcitationsofHandHe+from1sto2sand1sto2pbelow100eVarealsopresentedandthestructureoftheDCSsisanalyzed.

[1] Madison D H, Shelton W N. Distorted-wave approximation and its application to the differential and integrated cross sections for electron-mpact excitation of the 21P state of Helium [J].Phys.Rev. A, 1973, 7: 499.

[2] Bartschat K, Madison D H. Electron impact excitation of rare gases: differential cross sections and angular correlation parameters for neon, argon, krypton and xenon [J].J.Phys. B, 1987, 20: 5839.

[3] Madison D H, Winters K H. A second-order distorted-wave model for the excitation of the 21P state of helium by electron and positron impact [J].J.Phys. B, 1983, 16: 4437.

[4] Zeman V, Bartschat K. Electron-impact excitation of the (2p53s) and (2p53p) states of neon [J].J.Phys. B, 1997, 30: 4609.

[5] Bray I, Stelbovics A T. Convergent close-coupling calculations of electron-hydrogen scattering [J].Phys.Rev. A, 1992, 46: 6995.

[6] Khakoo M A, Wrkich J, Larsen M,etal. Differential cross sections and cross-section ratios for the electron-impact excitation of the neon 2p53s configuration [J].Phys.Rev. A, 2002, 65: 062711.

[7] Tong X M, Zhao Z X, Lin C D. Correlation dynamics between electrons and ions in the fragmentation of D2 molecules by short laser pulses [J].Phys.Rev. A, 2003, 68: 043412.

[8] Liang Y Q, Chen Z G, Madison D H,etal. Calibration of distorted wave Born approximation for electron impact excitation of Ne and Ar at incident energies below 100 eV [J].J.Phys. B, 2011, 44: 085201.

[9] Staudte A, Ruiz C, Schoffler M,etal. Binary and recoil collisions in strong field double ionization of helium [J].Phys.Rev.Lett., 2007, 99: 263002.

[10] Rudenko A, Jesus V L B de, Ergler Th,etal. Correlated two-electron momentum spectra for strong-field nonsequential double ionization of He at 800 nm [J].Phys.Rev.Lett., 2007, 99: 263003.

[11] Weber Th, Giessen H, Weckenbrock M,etal. Correlated electron emission in multiphoton double ionization [J].Nature, 2000, 405: 658.

[12] Chen Z J, Liang Y Q, Lin C D. Quantum theory of recollisional (e, 2e) process in strong field nonsequential double ionization of helium [J].Phys.Rev.Lett., 2010, 104: 253201.

[13] Chen Z J, Liang Y Q, Lin C D. Quantitative rescattering theory of correlated two-electron momentum spectra for strong-field nonsequential double ionization of helium [J].Phys.Rev. A, 2010, 82: 063417.

[14] Tong X M, Lin C D. Empirical formula for static field ionization rates of atoms and molecules by lasers in the barrier-suppression regime [J].J.Phys. B, 2005, 38: 2593.

[15] See Bray I, CCC-database, http://atom.curtin.edu.au/CCC-WWW/index.html.

[16] Khakoo M A, Larsen M, Paolini B,etal. Absolute differential cross sections for the electron impact excitation of the 12S→22S+22Plevels of atomic hydrogen at 50 and 100 eV [J].Phys.Rev.Lett., 1999, 82: 3980.

Calculation of differential cross sections for electron impact excitation of H and He+

LAI Zhuo-Jin, CHEN De-Feng, PAN Lin-Qing, JIANG Xiao-Han, XU Yong-Liang, CHEN Zhang-Jin

(College of Science, Shantou University, Shantou 515063, China)

We present the distorted wave Born approximation (DWBA) for electron impact excitation and a method to calibrate the DWBA. With the calibrated DWBA, the differential cross sections (DCSs) for excitation of H and He+from 1s to 2s and 2p are calculated and the results are compared with the absolute experimental measurements for H at incident energies of 50 eV and 100 eV. It has been found that the theoretical results are in very good agreement with experiment, which confirms the validity of the calibration procedure. This work prepares an efficient theoretical method for numerical simulations of non-sequential double ionization of He in strong laser pulse in which laser-induced electron impact excitation of He+is involved.

Electron impact excitation; Distorted wave Born approximation; Differential cross sections

2014-2-4

国家自然科学基金(11274219)；广东省高等学校人才引进项目；教育部留学回国人员启动基金项目；汕头大学科研启动经费项目

赖卓劲 (1992—)，男，广东人，主要从事原子与分子物理研究.

陈长进. E-mail: chenzj@stu.edu.cn

103969/j.issn.1000-0364.2015.08.013

O562.5

A

1000-0364(2015)08-0603-08