ZnO:Fe3+体系局域晶格结构的研究

李菊芬, 唐 斌，钟水蓉

(西南石油大学理学院，成都 610500)

ZnO:Fe3+体系局域晶格结构的研究

李菊芬, 唐 斌，钟水蓉

(西南石油大学理学院，成都 610500)

本文采用对角化三角场中d5组态离子的完全能量矩阵的方法，研究了Fe3+离子在ZnO:Fe3+体系的局域结构与EPR参量的关系，结果表明：在ZnO:Fe3+体系中，Fe3+取代了Zn2+离子后整个晶体显示出压缩畸变，其畸变参量ΔR=-0.119 Å和Δθ=0.339°被确定.

ZnO:Fe3+系统; 晶体局域结构畸变; EPR谱; 晶体场理论

1 前 沿

ZnO是一种重要的离子晶体，具有典型的三角四面体结构.近年来，各种过渡金属离子掺杂在ZnO中的EPR谱和ENDOR的研究引起了人们的极大兴趣.过渡金属Fe3+离子掺杂ZnO中,会出现明显的绿光发光特征，其发光强度随掺杂浓度增加先降低后增加.可制成的光电半导体，用在压敏变阻器、声表面波器件、气敏元件、紫外光探测等方面[1-3].

本文研究了过渡金属Fe3+离子掺入ZnO晶体中，其晶格上所产生的局域结构畸变.对于ZnO:Fe3+体系的光谱和EPR谱已经有很多科学家研究过.Heitz等[4]从实验上精确的测得ZnO:Fe3+体系4T(G)-6A(S)的基态跃迁光谱，并且确定4T(G)=1.78863±0.002 eV.而EPR谱，Dong等[5]用自旋-轨道原理和叠加模型研究了Fe3+离子掺杂到ZnO:Fe3+体系的EPR谱，他们认为Fe3+离子掺入ZnO晶体中后，Fe3+离子不能准确地占据Zn2+离子的位置，而是沿C3轴有一个位移.然而，在他们的研究中只考虑EPR二阶参量值D.一般描述Fe3+离子掺入ZnO：Fe3+体系的6A(S)态在三角场中的基态分裂的哈密顿量除了二阶参量D还包括四阶立方参量a和四阶低对称参量(a-F).所以仅仅用EPR二阶参量D来解释说明过渡金属离子所属晶格的局域微观结构的方法有时并不能得到唯一合理的解释.所以只有同时得到合理的基态零场分裂参量a、D和(a-F)，才能计算出与实验值相符合的基态零场分裂能级，同时也使局域结构的畸变在理论上得到合理的解释.

2 理论计算方法

ZnO:Fe3+体系的局域晶格具有C3点群对称性, 描述三角场中Fe3+离子的EPR谱的自旋哈密顿量算符为[6]：

s=gβ·/3]+

(1)

其中，a为EPR的立方参量，D和F参量分别与对称场中的二阶和四阶分量相联系，有(1)式可求得6A1基态零场分裂能级的解析表达式[7]：

E(±1/2)=(1/3)D-(1/2)(a-F)

-(1/6)[(18D+a-F)2+80a2](1/2),

E(±2/3)=-(2/3)D+(a-F),

E(±5/2)=(1/3)D-(1/2)(a-F)+

(1/6)[(18D+a-F)2+80a2](1/2)

(2)

Kuang曾经证明在Al2O3:Fe3+体系中D和(a-F)参量几乎不随a变化[8].计算表明上述结论对ZnO:Fe3+体系同样也成立.

在配位场理论下，描述三角场中Fe3+离子电子组态相互作用的微扰哈密顿量可以写成[9]：

=ee+so+CF

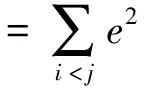
(3)

其中第一项表示电子与电子之间的相互作用；第二项表示电子的自旋-轨道耦合相互作用；第三项表示电子与配体间的相互作用；对于三角晶场有如下形式

θi,φi)+

(4)

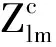
Zl0=Yl0,

(5)

这里Ylm是球谐函数.

B20=3G2(τ)(3cos2θτ-1)+G2(τ)(3cos2θτ-1),

B40=(3/4)G4(τ)(35cos4θτ-30cos2θτ+3)+

(1/4)G4(τ)(35cos4θτ-30cos2θτ+3)

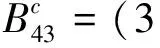
(√35/2)G4(τ)sin3θτcosθτ

(6)

(6)中式τ表示第τ个配体，θτ,Φτ表示第τ个配体的角度坐标，其中G2(τ), G4(τ)表示为

G2(τ)=-eqτG2(τ),G4(τ)=-eqτG4(τ)

这里G2(τ), G4(τ)描述配体场的强度.根据VanVleck关于Gk(τ)积分的近似表达式并采用点电荷模型，有以下关系：

G2(τ)= -eqτ/R3=A2/R3G4(τ)

= -eqτ/R5=A4/R5

(8)

这里A4=-eqτ, A2=-eqτ和A2/A4=/./=0.097是自由离子Fe3+的径向波函数得到的[10].由于LiAlO2和ZnO一样都是以氧为配体的四面体.所以(FeO4)5-团簇的值可以用Sherman测的LiAlO2:Fe3+体系的光谱来确定，并且在(FeO4)5-团簇里的Fe-O健长已经计算出来1.865 Å[11].这个健长与Y3Fe5O2化合物中(FeO4)5-团簇的Fe-O健长1.866±0.05 Å很接近[12].

利用公式(7)和(8)，Racah参量B=570cm-1,C=3180cm-1以及Fe-O健长1.865 Å，经拟和计算LiAlO2:Fe3+体系的光谱可得到团簇(FeO4)5-的A2和A4值,[11]及A4=32.00524a.u.,A2=3.105009a.u.(见表1).

对于ZnO:Fe3+体系的耦合系数ζ可通过EPR的立方参量a来确定.由104a=41.1cm-1的实验值可得到ζ=465.8cm-1[9].通过完全对角化能量矩阵，利用公式(6)和(8)将Fe3+在ZnO:Fe3+体系中的晶格结构和它的EPR谱关系建立起来.

3 具体计算

不纯离子在晶体中的EPR零场分裂对于结构的变化非常敏感.故可从零场分裂来研究晶体结构变化.对于Fe3+在ZnO:Fe3+体系中，铁离子取代锌离子的位置后被四个氧离子所包围(见图1).因为Fe3+离子的半径和有效电荷与Zn2+离子明显不同，所以Fe3+离子取代了Zn2+离子后结构一定会发生畸变.通过ΔR和Δθ来描述ZnO:Fe3+体系的三角畸变(见图2).对于Fe3+在ZnO:Fe3+体系中的结构参数R 、θ可以表示为

表1 在ZnO:Fe3 +体系中团簇(FeO4)5-的d-d跃迁值与LiAlO2:Fe3+体系观测值对比

Table1Comparisonbetweenthecalculatedd-dtransitionfor(FeO4)5-clusterinZnO:Fe3+systemandobservedinLiAlO2:Fe3+

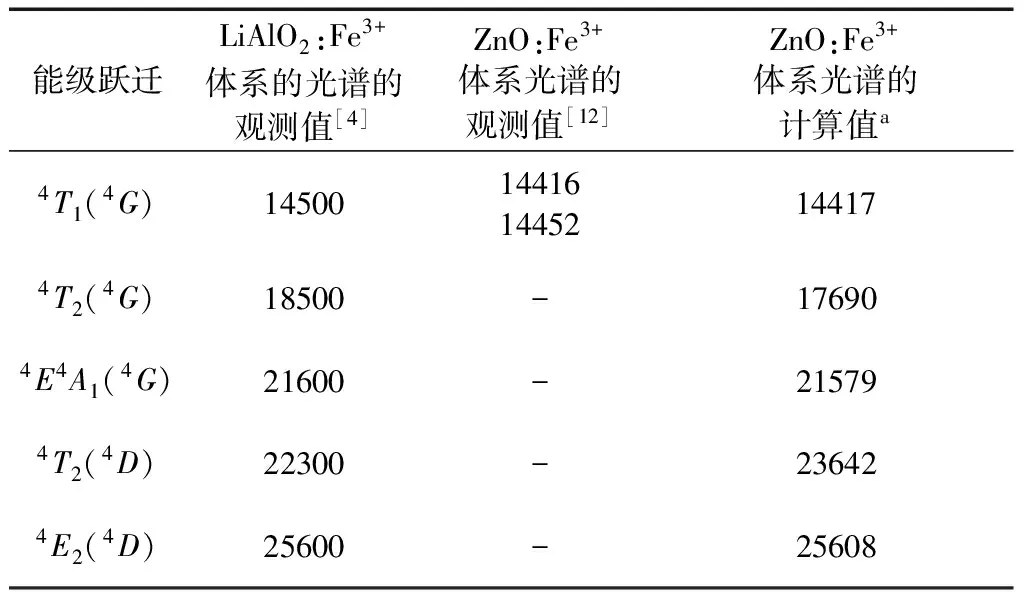
能级跃迁LiAlO2：Fe3+体系的光谱的观测值[4]ZnO：Fe3+体系光谱的观测值[12]ZnO：Fe3+体系光谱的计算值a4T1(4G)145001441614452144174T2(4G)18500-176904E4A1(4G)21600-215794T2(4D)22300-236424E2(4D)25600-25608

B=570cm-1,C=3180cm-1,A4=32.00524a.u.，所有能级的单位是cm-1

图1 ZnO:Fe3+体系结构图Fig.1 Local structure of ZnO:Fe3+ system

R1=R10+ΔR,R2=R20+ΔR,θ=θ0+Δθ

(9)

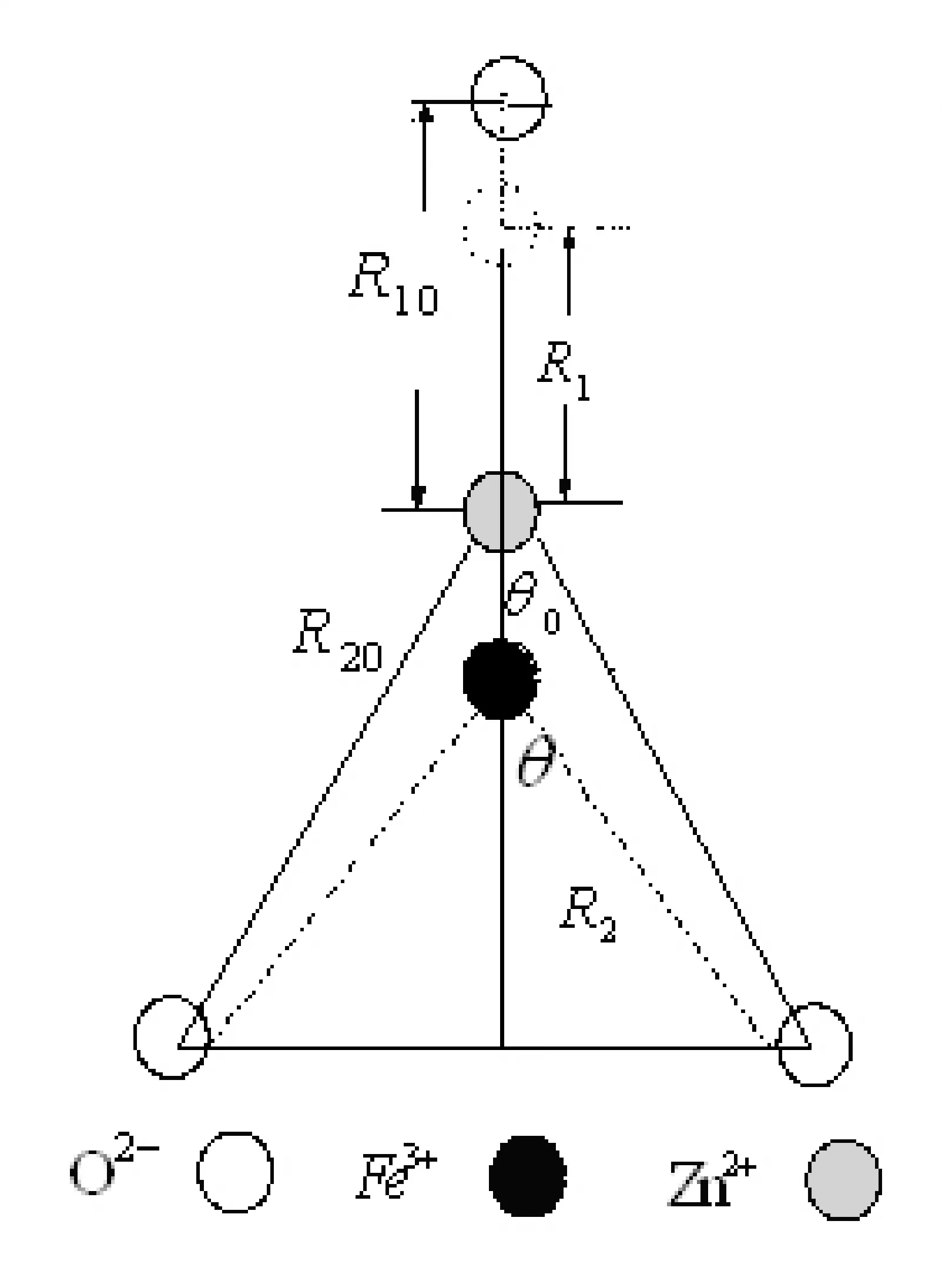
图2 Fe3+在ZnO:Fe3+体系结构畸变Fig.2 The local lattice structure distortion of Fe3+ in ZnO:Fe3+ system

其中6R10=1.97 Å,R20=1.98 Å, θ0=70.5288°.

将参数B=570cm-1,C=3180cm-1,ζ=465.8cm-1，A4=32.00524a.u．,A2=3.105009a.u.代入计算，并通过对角化能量矩阵可得到以ΔR和Δθ为函数的EPR参量值D和(a-F).计算结果列在表2中.从表中可看到当ΔR=-0.119 Å和Δθ=0.339°时，EPR参量的实验值可得到很好的解释.ΔR<0说明对于Fe3+在ZnO:Fe3+体系中有一个压缩的畸变.这些现象归因于两个事实，一是Fe3+离子的半径比Zn2+离子明显小；二是Fe3+离子有效电荷比Zn2+离子的大，故吸引力要强一些.

4 结 论

本文通过对角化完全能量矩阵，研究了ZnO:

表2 ZnO:Fe3+体系的EPR参量a、D和(a-F)值

104a,104D,104(a-F),104ΔE1,104ΔE2的单位是cm-1

Fe3+体系的基态零场分裂及晶体的局域结构的畸变.通过拟和EPR的D和(a-F)参量的实验值，发现当Fe3+离子取代Zn2+离子后，ZnO:Fe3+体系中以Fe3+离子为中心的四角场的局域晶格畸变的趋势是压缩的.这种现象归因于两个事实，一是Fe3+离子的半径比Zn2+离子明显小；二是Fe3+离子有效电荷比Zn2+离子的大，故吸引力要强一些.

[1]MizokawaT,NambuT，et al.Electroicstructureoftheoxide-dilutedmagneticsemiconductorZn1-xMnxO[J]. Phys. Rev.B, 2002, 65(8): 085209-1.

[2]JinZW,YooY-Z, et al.BlueandultravioletcathodoluminescencefromMn-dopedepitaxialZnOthinfilms[J].Appl. Phys.Lett., 2003, 83(1): 39.

[3]KaneMH, et al.MagneticpropertiesofbulkZn1-xMnxOandZn1-xCoxOsinglecrystals[J]. J. Appl.Phys., 2005, 97(2): 023906.

[4]HeitzR,HoffmannA,BroserI.Fe3+centerinZnO[J]. Phys. Rev.B, 1992, 45(16): 8977.

[5]DongHN,WuXX,WuSY, et al.StudiesondefectstructuresofMn2+andFe3+impuritycentersinZnOcrytsals[J].Acta Physics Sinica, 2002,51(3): 0616(inChinese)[董会宁，吴晓轩，邬劭轶，等.ZnO晶体中Mn2+与Fe3+杂质中心的缺陷结构研究[J].物理学报, 2002, 51(3): 0616]

[6]BleaneyB,TrenamRS.Paramagneticresonancespectraofsomeferricalumsandthenuclearmagneticmomentof57Fe[J]. Proc. R. Sol. London. Ser., 1954,A223: 1.

[7]AbragamA. Electron paramagnetic resonance of transition ions[M].Oxford:OxfordUniversityPress, 1986.

[8]KuangXY.Ground-statezero-fieldsplittingofMn2+ionsinZnOandCdSecrystals[J]. Phys. Lett.A, 1996, 213: 89.

[9]KuangXY.AnalysisoftheelectronParamagneticresonancezero-fieldsplittingforFe3+insapphire[J]. Phys. Rev.B, 1987, 36(1): 712.

[10]KuangXY.Theoryofcovalentmagneticexchangeinteractionforapplicationdiiron(III)coreintheactivesiteofribonucleotidereductase[J]. Phys. Lett.A, 2002, 293: 293.

[11]ShermanDM.TheelectronicstructuresofFe3+coordinationsitesinironoxides[J]. Phys. Chem. Miner., 1985, 12: 161.

[12]EulerF,BruceJA.Oxygencoordinatesofcompoundswithgarnetstructure[J]. Acta Crystallogr., 1965, 19: 971.

EPR theoretical study of local molecular structure for tetrahedral Fe3 +centers in zinc oxide

LI Ju-Fen, TANG Bin, ZHONG Shui-Rong

(School of Science, Southwest Petroleum University, Chengdu 610500, China)

The electron paramagnetic resonance spectrum of the ZnO:Fe3+system has been studied on the basis of the complete energy matrices of d5configuration ion with a trigonal symmetry. The results indicate that the local lattice structure around tetrahedral Fe3+centers exhibits a compression distortion. The local lattice structure distortion parameters ΔR=-0.119 Å and Δθ=0.339° for Fe3+ion in ZnO:Fe3+system are determined.

ZnO:Fe3+system; Local lattice structure distortion; EPR spectrum; Ligand-field theory

四川省教育厅面上基金资助项目(11ZB019); 西南石油大学校级科技基金项目(2012XJZ028)

李菊芬(1978—),女，讲师,主要从事晶体材料研究.E-mail： swpu-ljf@163.com

103969/j.issn.1000-0364.2015.08.003

0433

A

1000-0364(2015)08-0543-04

投稿日期:2014-09-08