相似线性变换及其性质

卢家宽，梁美花，王凤娟，吴开迅

(广西师范大学 数学与统计学院，广西 桂林 541004)

线性代数是研究有限维线性空间的理论与方法的一门学科，是高等院校里理工农医等专业最为重要的数学基础课程之一，也是数学专业的重要基础课程，是考研必考科目之一。瑞典数学家戈丁在其名著《数学概观》中说:“如果不熟悉线性代数的概念，要去学习自然科学，现在看来就和文盲差不多。”［1］

线性空间与线性变换是线性代数的主要研究对象，而矩阵是线性代数的重要工具和核心思想。线性代数的许多问题都可以用矩阵的语言来描述，并转化为矩阵的运算，也只有如此，才能达到最为有效的处理。例如文献［2－3］对此都有体现。

设矩阵A，B∈Mn(K)，如果存在可逆矩阵P∈Mn(K)，使得B=P－1AP则称矩阵B与A相似。记作A～B.矩阵的相似关系是矩阵间的一种重要关系，在矩阵理论和其他学科有许多应用，许多学者对相关问题进行了研究。例如，R.Bhatia［4］研究了两个n阶方阵A，B的乘积AB和BA的许多相同的重要性质，比如它们的特征值、特征多项式以及秩和行列式相同。我们自然地考虑AB和BA是否相似的问题，事实上，已经有人讨论了该问题，但未给出完整的解答［5］。李亦芳等［6］讨论了相似矩阵的性质及应用，而丁春荣等［7－8］研究了相似关系在计算机理论中的应用。

由线性代数的理论，我们知道:取定线性空间的一个基，那么线性变换在该基之下对应唯一的矩阵。受此启发，本文定义线性变换的相似关系:

定义1.1 设σ，τ∈HomK(V)，如果存在可逆的 ρ∈HomK(V)，使得τ=ρ－1σρ，则称 τ与 σ 相似，记作σ ～τ.

本文首先给出相似线性变换的一些基本性质，然后讨论线性变换的特征定理和相似不变量。

本文使用到主要符号约定:设K为数域，数域K上所有n阶矩阵的全体记为Mn(K).令V为数域K上的n维线性空间，V的所有线性变换的全体记为HomK(V).由线性代数的理论，我们知Mn(K)≅HomK(V).在本文里，除非有特别说明，所考虑的线性空间都是n维的，方阵都是n阶的。

1 相似线性变换的性质

这一节给出相似线性变换的若干基本性质。首先，线性变换的相似关系是一种等价关系，即具有以下性质:

(1)自反性:对任意σ∈HomK(V)，σ与它自己相似，即σ～σ，这是因为σ=ι－1σι，其中ι是V的恒等变换;

(2)对称性:对任意 σ，τ∈HomK(V)，如果 σ ～τ，那么 τ～σ，这是因为 τ =ρ－1σρ蕴含 σ =(ρ－1)－1τρ－1，其中ρ是V的可逆变换;

(3)传递性:对任意 σ，τ，φ∈HomK(V)，如果 τ～σ，σ ～φ，那么 σ ～φ. 事实上，由 τ=ρ－1σρ，σ =φ－1φφ，有 τ=(φρ)－1φφρ.

关于相似线性变换，还有以下性质。

命题2.1 若σ～τ，则αm～τm，其中m是非负整数。

证明:设 σ ～ τ，则存在可逆的 ρ，使得 τ=ρ－1σρ. 于是

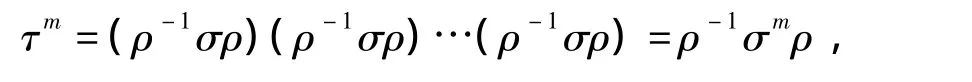
故 αm～τm.证毕。

命题2.2 若σ～τ，则kα～kτ，其中k是非负整数。

证明:设 σ ～ τ，则存在可逆 ρ，使得 τ=ρ－1σρ. 于是

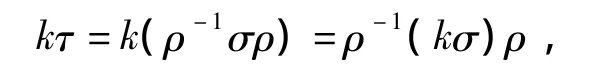
故kσ ～kτ.证毕。

更一般地，有如下结论。

命题2.3 设 σ ～τ，f(x)∈K［x］，则有f(σ)～f(τ).

证明:因为 σ ～ τ，所以存在可逆线性变换 ρ，使得 τ=ρ－1σρ. 则有 τi=(ρ－1σρ)i=ρ－1σiρ.

设f(x)=a0+a1x+…+anxn.于是，

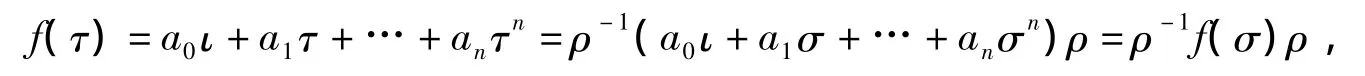
即f(σ)～f(τ).证毕。

注记2.4 设 σ ～τ，f(x)，g(x)∈K［x］，则f(σ)与g(τ)不一定相似。

取f(x)=a0+a1x+ … +anxn，g(x)=b0+b1x+… +bnxn.

取a0=a1=…=an=0，即f(x)=0，于是f(σ)=0.任取一个可逆线性变换φ，则φ－1f(σ)φ=0.

当b0，b1，…，bn不全为零时，有g(x)≠0，使得g(τ)≠0. 即任取 φ，都有 φ－1f(σ)φ≠g(τ).所以f(σ)与g(τ)不相似。

2 相似线性变换的特征定理

下面的定理指出两个线性变换相似当且仅当它们在线性空间的某个基之下的矩阵相似。这为后面讨论线性变换的相似不变量提供了工具。

定理3.1 设σ，τ是n维线性空间V上的两个线性变换，且它们在V的基α1，α2，…，αn下的矩阵分别为 A，B，则A～B的充分必要条件是σ～τ.

证明:如果τ与σ 相似，则存在可逆的ρ∈HomK(V)，使得τ =ρ－1σρ. 设ρ在基α1，α2，…，αn之下的矩阵为P.则有B=P－1AP，即A与B相似。

反之，设 A ～B，即存在可逆n阶矩阵 P，使得 P－1AP=B.对V的任意向量 α=(α1，α2，…，αn)x，令

ρ(α)=(α1，α2，…，αn)Px，其中x是 α 在 α1，α2，…，αn之下的坐标列。则易检验:ρ是V的线性变换，且 ρ在α1，α2，…，αn之下的矩阵为 P. 进一步，我们有故 ρ－1σρ=τ，即 τ与 σ 相似。证毕。

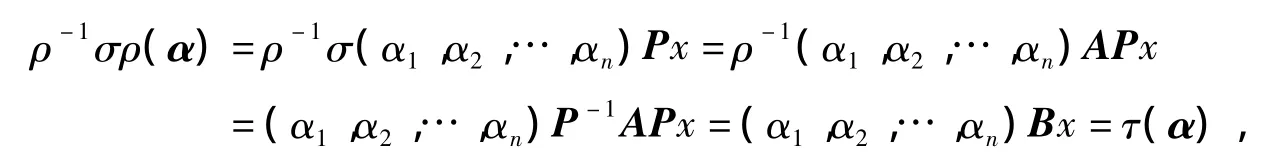
由线性代数的知识知:数域K上两个矩阵A，B相似当且仅当存在线性空间的线性变换σ以及两个基，使得σ在这两个基之下的矩阵分别为A，B(例如，见参考文献［9］)。对线性变换的相似关系也有类似的结论。

定理3.2 设 σ，τ∈HomK(V)，若 τ与 σ 分别在V的基 α1，α2，…，αn和 β1，β2，…，βn之下的矩阵相同，则σ与τ相似。

证明:设 τ 与 σ 分别在V的基 α1，α2，…，αn和 β1，β2，…，βn之下的矩阵都为 A，且

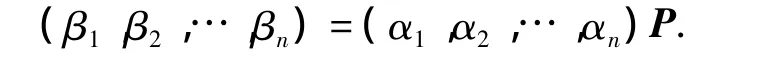
则σ在β1，β2，…，βn之下的矩阵为B=P－1AP.由定理3.1知，σ与τ相似。证毕。

定理3.2的逆命题也成立。

定理3.3 设 σ，τ∈HomK(V)，若 τ与 σ 相似，则存在V的基 α1，α2，…，αn和 β1，β2，…，βn，使得 σ 在α1，α2，…，αn之下的矩阵恰好等于 τ在 β1，β2，…，βn之下的矩阵。

证明:任取V的基 α1，α2，…，αn.设 σ 在 α1，α2，…，αn之下的矩阵为 A.由于 τ 与 σ 相似，故可设 τ=ρ－1σρ，其中，ρ∈HomK(V). 令 ρ在 α1，α2，…，αn之下的矩阵为 P. 则 P 可逆。令

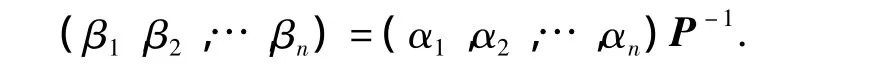
则 β1，β2，…，βn是V的基，且 ρ在 β1，β2，…，βn之下的矩阵也为 P. 于是

即 σ 在 β1，β2，…，βn之下的矩阵为 A. 证毕。

定理3.2和3.3合起来叙述成:

定理3.3 两个线性变换相似的充分必要条件为它们在线性空间的两个基下的矩阵相同。

3 线性变换的相似不变量

由线性代数理论知:设σ∈HomK(V).如果存在V的非零向量ξ，使得σ(ξ)=λξ，则称λ为σ的一个特征值，而非零向量ξ称为σ的属于特征值λ的一个特征向量。规定:Vλ={ξ∈V|σ(ξ)=λξ}，则易见Vλ是V的子空间，称为V的属于λ的特征子空间。

特征值、特征向量是数学里非常重要的概念之一，不少文献对此有讨论，如文献［10］。下面讨论相似线性变换的特征值、特征向量之间的联系。

定理4.1 设σ，τ为n维线性空间V上的线性变换，且有σ～τ，那么σ，τ有相同的特征值。

证明:如果σ与τ相似，则由定理3.1知，σ与τ在V的某个基α1，α2，…，αn之下的矩阵相似。而相似的矩阵有相同的特征值，故σ与τ有相同的特征值。证毕。

另证:如果τ与σ相似，则存在可逆的ρ∈HomK(V)，使得τ=ρ－1σρ.设λ是σ的任意特征值，α是σ的属于 λ 的特征向量，即 σ(α)=λα，0≠α∈V. 则 ρτρ－1(α)= λα，即 τρ－1(α)= λρ－1(α). 由于 α≠0，所以ρ－1(α)≠0.这说明λ是τ的特征值，ρ－1(α)是τ的属于λ的特征向量。反之亦然。证毕。

第二种证明方法略显繁杂，但从中可以看到:

注记4.2 若σ～τ，则它们的特征向量不一定相同。由于σ～τ，则存在可逆ρ，使得τ=ρ－1σρ.设σ，τ有相同的特征值 λ。故存在V的非零向量 β，使得 τ(β)=λβ.于是 ρ－1σρ(β)=λβ，即 σ(ρ(β))=λ(ρ(β)).于是ρ(β)≠0是σ的属于λ的特征向量。取ρ为位似变换，则ρ(β)=kβ，其中k≠0.即得kβ=α.当k≠1时，α≠β.所以σ～τ时，它们的特征向量并不一定相同。

定理4.3 设σ，τ为n维线性空间V上的线性变换，且α～τ，则它们属于同一特征值的特征子空间同构。

证明:由于σ～τ，则存在可逆ρ，使得τ=ρ－1σρ.设σ，τ有相同的特征值λ.故存在V的非零向量β，使得 τ(β)=λβ. 于是 ρ－1σρ(β)=λβ，即σ(ρ(β))=λ(ρ(β)). 于是 ρ(β)≠0 是 σ 的属于 λ 的特征向量。因为ρ可逆，故ρ为双射线性变换。于是ρ为α的特征子空间到τ的特征子空间的同构映射，所以α的特征子空间与τ的特征子空间同构。

［1］戈丁.数学概观［M］.胡作玄，译.北京:科学出版社，2001.

［2］王卿文.线性代数核心思想及应用［M］.北京:科学出版社，2013.

［3］Sheldon Axler.Linear algebra done right［M］.New York:Springer－ Verlag Inc，1997.

［4］R Bhatia.Eigenvalues ofABandBA［J］.Resonance，2002(7):88 －90.

［5］张会平.一类矩阵相似性的研究［J］.厦门大学学报(自然科学版)，2010，49:597－601.

［6］李亦芳，张环理，张丹.相似矩阵的性质及应用［J］.河南教育学院学报(自然科学版)，2005，14:11－12.

［7］丁春荣，李龙澎.基于相似关系向量的改进ROUSTIDA算法［J］.计算机工程与应用，2014，50:133－136.

［8］邹万杰，陆国东，陆进.基于残余力向量的框架损伤直接识别法［J］.广西科技大学学报，2014，25:21－30.

［9］易忠.高等代数与解析几何［M］.北京:清华大学出版社，2007.

［10］赵展辉.分块三角矩阵的一类特征子空间［J］.广西工学院学院，1995，6:1－4.