大涵道比风扇转子的非定常数值模拟

解亚东，朱 贤，丁建国

（中航工业商用航空发动机有限责任公司，上海201108）

大涵道比风扇转子的非定常数值模拟

解亚东，朱 贤，丁建国

（中航工业商用航空发动机有限责任公司，上海201108）

为了更好地设计大涵道比风扇转子及外涵导叶(O G V)，采用非线性谐波法对某大涵道比风扇转子及O G V进行了非定常和定常数值计算，2种计算方法获得的风扇外涵级的流量、增压比、绝热效率有一定差异，并分析了性能变化的原因。通过对其典型截面的非定常流场进行快速傅里叶分解，在频域内分析了风扇转子和O G V之间的转静干扰效应，以及交界面典型脉动量的周向波形，从频域的角度分析了影响性能的原因；同时观察到一些时域中难呈现的现象。结果表明：通过非定常数值计算，大涵道比风扇外涵级绝热效率曲线随时间变化呈现正弦曲线的形状，幅值约为0.59个百分点；风扇外涵级绝热效率最高、最低点分别出现在风扇尾迹通过静子通道的约3/4和1/4处。

大涵道比风扇转子；非线性谐波法；非定常计算；时域分析；频域分析

0 引言

国内外风扇数值模拟普遍采用3维定常和非定常模拟技术。定常模拟比非定常模拟的计算量小，广泛应用于工程设计，但是在处理多叶片排交界面时，采用掺混面平均的方式而忽略了上下游的非定常相互作用。非定常模拟相对完整地保留了其技术细节，但是计算量庞大，难以用于工程设计。1985年，美国NASA刘易斯研究中心的Adamczyk[1]引入了3个平均算子，建立了描述叶轮机内确定性非定常流动的通道平均方程(Average Passage Equations)，目的是通过引入确定性应力来反映转静干涉对时均流动的影响。正如雷诺平均带来的“雷诺应力”模化难题一样，Adamczyk的通道平均方法引入了“确定应力”的建模难题。为此，20多年来，国内外学者进行了许多创新性研究[2-6]。1992年，Giles提出了渐进求解的思路[7]，其后，在其启发下进行了创造性发展[8-9]，开发了非线性谐波法(frequency based nonlinear harmonic method，以下简称NHM)。该方法将非定常流场分成时均和脉动流场2部分进行耦合求解，分别通过求解含有决定性应力的时均流动方程和在频域内N阶谐波得到。在确定应力建模方法方面较严谨、精度较高，不需要经验参数，应用范围较广。在工程应用中[10-12]，一般只需要前2～3阶谐波[13-14]就可以较好地模拟确定性应力。

本文以某大涵道比风扇转子及外涵出口导叶（OGV）为第1级，进行了定常和非定常计算，并在时域层面上分析了级间性能的差异。通过对典型截面非定常流场的FFT分解得到各物理量的频谱图域，分析了转静干涉现象和典型截面脉动量周向波形。

1 数值方法

1.1 定常和非定常计算

采用商用软件NUMECA对某风扇转子及OGV进行了定常和非定常计算。其中风扇和OGV的叶片数目分别为18、55。

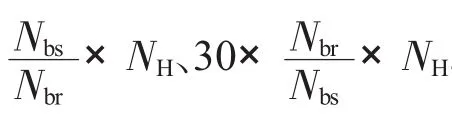
为了减小网格对定常和非定常计算结果的影响，均采用相同的网格数目及拓扑结构，湍流模型一致，且内外涵道均采用静压边界条件，如图1所示。

图1 3维网格

1.2 快速傅里叶分解

在非定常计算结果中，空间每点物理量非定常时变曲线包含64个点，延拓为8个周期后进行快速傅里叶变换（FFT）计算，来提高采样精度，并保存前3阶谐波的实部和虚部。

OGV进口处某一点轴向速度的时域和频域曲线分别如图2、3所示。从图3中可见，在0 Hz处的幅值（轴向速度的均值）最高。OGV轴向速度频域各基频和倍频曲线如图4所示，是前3阶频率下轴向速度脉动值的放大显示。其中基频及各倍频以外的频率对应的幅值很小，可见时域曲线的周期性良好。

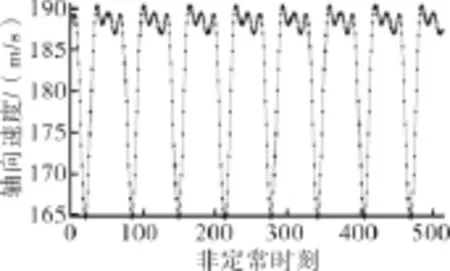
图2 OGV轴向速度的时域曲线

图3 OGV轴向速度的频域曲线

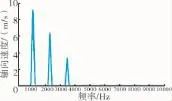
图4 OGV轴向速度频域各基频和倍频曲线

2 时域分析

2.1 非定常流场时域流场的分析

风扇转子和OGV组合为外涵的第1级，其非定常计算的级绝热效率分布如图5所示，OGV非定常计算总压恢复系数分布如图6所示。从图中可见，级绝热效率分布类似于正弦曲线，幅值约为0.59个百分点，与试验结果[15]吻合。级最高、最低效率点分别出现在转子转过0.765倍、1/4的OGV通道周向弧长处。风扇转子非定常计算绝热效率分布如图7所示。从图中可见，非定常计算对风扇转子的效率影响较小，由于风扇转子和OGV的轴向长度是1个风扇转子中径的弦长，尾迹的影响仅仅往下游传播，势流影响在向上游传播时经过较长距离，耗散较多，对风扇转子效率的影响较小。这也可从后面的频域分析得知。

图5 风扇转子和OGV非定常级绝热效率分布

图6 OGV非定常计算总压恢复系数分布

图7 风扇转子非定常计算绝热效率分布

由于OGV受风扇转子尾迹和势流影响较大，会出现总压恢复系数类似于级效率分布曲线。OGV吸力面相对静压分布如图8所示。从图中可见，Ps、Paver作为无量纲物理量来显示细微差别，分别指静压和转静交界面处的平均静压。在吸力面叶中位置，最大效率比最小效率处的最大静压降略微靠近前缘。OGV压力面相对静压分布如图9所示。从图中可见，在70%叶高位置，最大比最小效率处的高静压分布范围更广。说明了尾迹在扫掠OGV通道的不同位置会带来不同的静压分布，这也是导致效率高低的原因。

图8 OGV吸力面相对静压分布

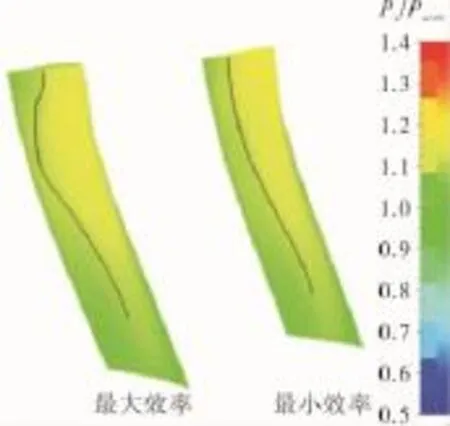
图9 OGV压力面相对静压分布

在设计点处且级压比不变的情况下，非定常计算外涵流量和风扇转子绝热效率比定常计算的分别增加0.00401%、0.07%。非定常计算OGV总压恢复系数比定常计算的减小0.83%，级绝热效率提高0.05%。2种计算结果非常近似。这主要是由于风扇转子和OGV轴向距离太远，尾迹和势流对性能的影响较小。

3 频域分析

3.1 频域流场的分析

叶中截面轴向速度第1阶谐波实部如图10所示。从图中可见，OGV图像呈条带形，走向，与尾迹方向相同。尾迹在扫掠过的区域的特点是以时间为横坐标的流场参数的时变曲线初始相位角近似，N阶谐波的实部/虚部是幅值和该角度的正弦函数/余弦函数的乘积，所以在该角度下进行FFT分解会保证实部（或虚部）在尾迹扫掠过区域的取值近似相等。条文呈正负交替也是由于正、余弦函数正、负的特点所致。

图10 叶中截面轴向速度1阶谐波实部

通过非定常的参数计算得出，OGV计算域内包含3～4条条带。OGV通道长度为0.5048 m，轴线速度约为180 m/s，扫掠周期为8.6557×10-4s，通过时间为2.802×10-3s，OGV区域内尾迹条数为后者与前者的比值3.239，与频域内的条代数基本吻合。

近轮毂截面和机匣截面周向速度的第1阶谐波实部分布分别如图11、12所示。从图中可见，条带分布规律大体与叶中的类似。由于上游转子出口的气流角和轴向速度周向分布的不同导致条带走向和幅值存在差异。其中在叶根处轴向速度的幅值要高于叶尖处的，中间截面最大，即在叶尖处的尾迹影响比叶中和叶根都偏小，所以需要改善风扇转子的叶中和叶根。以下为叶中典型界面的分析。

图11 5%叶展截面周向速度第1阶谐波实部

图12 95%叶展截面周向速度第1阶谐波实部

轴向速度第1阶谐波的幅值分布如图13所示。由于交界面是OGV中非定常扰动的源头，非定常尾迹干扰通过此处向下游传播，所以从图中可见在交界面处幅值最大。同时幅值延轴向衰减，如图14所示。

图13 轴向速度第1阶谐波幅值

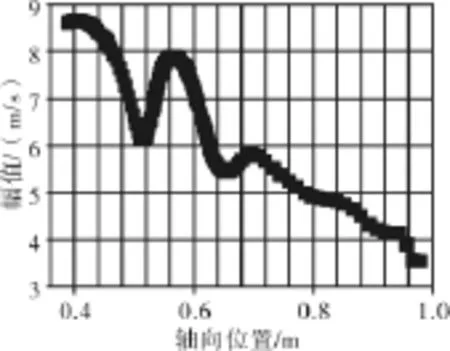
图14 轴向速度第1阶幅值沿轴向衰减

轴向速度第 2阶谐波实部如图15所示。从图中可见，频率增加，对应的波长缩短，导致条纹比第1阶谐波密。轴向速度第3阶谐波实部如图16所示。从图中可见，条纹变得更密。

图15 轴向速度第2阶谐波实部

图16 轴向速度第3阶谐波实部

综上所述，谐波频率越高，实部幅值越小且轴向衰减速度越快。

第1～3阶谐波实部进口处的周向波形如图17所示。从图中可见，随着谐波阶数的增加，所包含的周期性也增加。

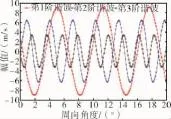
图17 OGV进口周向速度前3阶谐波实部周向波形

切向、径向速度和密度等因素受尾迹影响，其频谱图谱与轴向速度类似，这里暂不讨论。静压的分部则明显不同。叶中截面静压第1阶谐波实部如图18所示。从图中可见，由于静压受尾迹影响小，更多受叶片势流干扰。

图18 叶中截面静压第1阶谐波实部

上文针对OGV通道中的分部进行分析，下文进行风扇转子通道中轴向速度分析。

叶中截面轴向速度第1阶谐波实部如图19所示。从图中可见，风扇转子通道中的第1阶谐波也呈条带状。轴向速度的第1阶谐波幅值也是在交界面处最大，但是幅值很小，表明下游OGV对上游风扇转子的势干扰较弱，幅值在风扇转子通道中衰减更快，如图20所示。

图19 叶中截面轴向速度第1阶谐波实部

图20 叶中截面轴向速度第1阶谐波幅值

4 结论

（1）在设计点处，采用3阶非线性谐波法进行了非定常计算；与定常计算相比，大涵道比风扇转子和OGV的流量、压比、绝热效率有一定差异，但由于其轴向间距较大，其差异不大。

（2）通过非定常计算可以得出大涵道比风扇转子和OGV级绝热效率曲线随时间变化呈现正弦曲线，幅值约为0.59个百分点。

（3）通过非定常计算可以得出风扇转子和OGV级绝热效率最高、最低点分别出现在风扇尾迹通过静子通道约3/4和1/4处。

综上所述，通过对频域图谱的研究，从新的视角分析了风扇外涵道级非定常流场。

[1]Adamczyk J J.Model equation for simulation flows in multi stage turbomachinery[R].ASME 85-GT-226.

[2]Adamczyk J J.A model for closing the inviscid form of the average passage equation system[J].Journal of Turbinemachinery，1986，108（2）：180-186.

[3]Rhie C M，Gleixner A J，Spear D A，et al.Development and application of a multistage Navier-Stokes solver-PartⅠ：multistage modeling using body-forces and deterministic stresses[R].ASME 95-GT-342.

[4]Sondak D L，Dorney D J，Davis R L.Modeling turbomachinery unsteadiness with lumped deterministic stresses[R].AIAA-1996-2570.

[5]AGVD Wall，JR Kadambi，JJ Adamczyk.A transport model for the deterministic stresses associated with turbomachinery blade row interaction[J].Journal of Turbomachinery，2000，122（4）：593-603.

[6]季路成.轴流式叶轮机转子/静子干扰非定常流动探索研究[D].北京：北京航空航天大学，1998. JI Lucheng.Research on rotor/stator interaction in axial turbomachinery [D].Beijing：Beihang University，1998.（in Chinese）

[7]Giles M.An approach for multistage calculations incorporating unseadiness[R].ASME 92-GT-282.

[8]He L，Ning W.Efficient approach for analysis of unsteady viscous flows in turbomachines[J].AIAA Journal，1998，36（11）：2005-2012.

[9]Chen T，Vasanthakumar P，He L.Analysis of unsteady blade row interaction using nonlinear harmonic approach[J].Journal of Propulsion and Power，2001，17（3）：651-658.

[10]Martens S，Shin H，Gliebe P.Rotor wake unsteady flow field hot-wire measurements in the universal propulsion simulator(UPS)at NASA[R].GE Aircraft Engines TM 97-67.

[11]GanzU W.Experimental investigation of the unsteady flow characteristics in the Boeing 18 inch fan rig[R].AIAA-99-1886.

[12]Verhoff V G.Three dimensional laserwindow formation[R]. NASA-RP-1992-1280.

[13]赵军，柳阳威，刘宝杰.ASA67级非定常流场的频域分析[J].航空动力学报，2007，22（8）：1371-1377. ZHAO Jun，LIU Yangwei，LIU Baojie.Frequency-domain analysis of NASA67 unsteady flow field[J].Journal of Aerospace Power，2007，22（8）：1371-1377.（in Chinese）

[14]李翔.1.5级涡轮非定常流动研究 [D].哈尔滨：哈尔滨工程大学，2010. LI Xiang.Unsteady flow investigation of a 1.5-stage axial turbine[D]. Harbin：Harbin Engineering University，2010.（in Chinese）

[15]Städing J，Friedrichs J，Waitz T，et al.The potential of rotor and stator clocking in a 2.5-stage[C]//ASME TURBO EXPO 2012. Copenhagen，Denmark：GT2012-68353，2012.

（编辑：肖磊）

Unsteady Numerical Simulation of High Bypass Ratio Fan

XIE Ya-dong，ZHU Xian，DING Jian-guo
（AVIC Commercial Aircraft Engine Co.Ltd.，Shanghai 201108，China）

The unsteady and steady numerical calculation of a high bypass ratio fan and OGV were obtained by non linear harmonic method to design them better.The bypass flows pressure ratio,stage adiabatic efficiency of the fan which got from the two simulation methods were different,and the reasons were analyzed.Based on the Fast Fourier Transformation (FFT)of the typical profiles of the stage, the rotor-stator interactions between the fan and OGV were analyzed,and the circumferential distribution of typical unsteady perturbation was studied to give out the influences reason in the frequency domain.The phenomena hardly observed in the time domain can be discovered simultaneously.The results show that the stage adiabatic efficiency of the high bypass ratio fan is a sinusolid according to the time,and the amplitude value is about 0.59 percent according to unsteady numerical calculation.The maximum and minimum value of the stage adiabatic efficiency is located on 3/4 and 1/4 OGV that the fan wake passed through.

high bypass ratio fan； non linear harmonic method；unsteady calculation；time domain analysis；frequency domain analysis

V 211.45

A

10.13477/j.cnki.aeroengine.2015.05.004

2014-07-24

解亚东（1987），男，硕士，从事风扇/增压级气动性能设计工作；E-mail：xieyadong163@163.com。

解亚东，朱贤，丁建国.大涵道比风扇转子的非定常数值模拟[J].航空发动机，2015，41（4）：20-23.XIE Yadong，ZHUXian，DING Jianguo.Unsteady numerical simulation ofhigh bypass ratiofan [J].Aeroengine，2015，41（4）：20- 23.