旋转进口畸变频率对跨声速压气机稳定性影响的数值研究

谢 喆，柳阳威，刘小华，孙晓峰，陆利蓬

（1.北京航空航天大学航空发动机气动热力国家科技重点实验室，北京100191；2.先进航空发动机协同创新中心，北京100191）

旋转进口畸变频率对跨声速压气机稳定性影响的数值研究

谢 喆1，2，柳阳威1，2，刘小华1，2，孙晓峰1，2，陆利蓬1，2

（1.北京航空航天大学航空发动机气动热力国家科技重点实验室，北京100191；2.先进航空发动机协同创新中心，北京100191）

为了研究旋转进口畸变对于压气机失速过程的影响，以及探讨最易诱发压气机失速的扰动频率即特征频率存在性的问题，采用非定常方法计算研究了4种不同频率的进口旋转畸变对跨声压气机Rotor37失速起始过程的影响。结果表明：在同样幅值条件下，当旋转频率与失速扰动频率相近时的畸变会引起失速，反之亦然；进口畸变的低压区引起部分叶片通道内流动结构失稳后，在叶尖泄漏涡破碎的作用下通道内形成严重堵塞，从而导致压气机失速。该方法能够较好地描述转子中失速团的发展过程，同时得出了进口畸变频率对失速过程影响的物理机制。

进口畸变；旋转失速；扰动频率；叶尖泄漏；跨声速压气机；稳定性；数值模拟

0 引言

现代飞机不断提高的技术指标要求航空发动机具备高可靠性和稳定性[1]，而在小流量工况下旋转失速问题正是限制压气机有效工作范围的主要原因之一。因此，需要在设计过程中进行准确预测和有效控制，但由于失速过程中压气机内出现叶尖间隙泄漏流、叶片吸力面分离流、前缘溢流、尾流倒流等多种非定常流动，并且旋转失速需要整圈多排的跨尺度非定常计算，耗费非常大而无法在工程上广泛应用。因此，建立较为准确的工程适用的压气机稳定性预测模型和数值方法，具有重要的科学意义和工程意义。

早在1974年Nenni和Ludwig[2]基于小扰动理论线性化了2维简化的单排叶片模型，通过激盘模型的假设得到了单、双排叶栅的2维不可压旋转失速稳定性模型；Greitzer[3-4]提出的基于压缩系统理论的压气机稳定性模型为简化激盘1维非线性模型，用于预测受到扰动后轴流式压缩系统的瞬时流场变化情况；之后，Moore和Greitzer[5-6]将此模型发展到2维不可压流动中，使得模型能够同时应对压气机喘振、失速的稳定性分析并且提供了预测失速后非线性现象的方法；孙晓峰[7-8]利用3维可压缩的线性化非定常Euler方程发展出可以考虑任意阶径向扰动的3维可压缩旋转失速稳定性模型；孙晓峰[9]等在该模型理论基础上进一步发展，从基本的N-S方程出发，发展了叶轮机内部流动失稳的通用稳定性理论，将一般的流动稳定性问题转化为系统的特征值方程来求解压气机的稳定性问题，能够较为准确地预测压气机失稳工况点和在该工况点最易引发失速的进口畸变扰动频率，即特征频率。

本文在文献[9]的研究基础上，采用3维非定常CFD技术数值研究旋转进口总压畸变频率对某跨声压气机稳定性影响。以高速跨声压气机Rotor37为例，模拟了不同进口畸变扰动频率下压气机流动情况，根据出现失速现象的工况分析了进口旋转畸变导致压气机失速的机理。

1 研究对象及数值方法

1.1 压气机转子以及进口旋转畸变的选择

NASA Rotor37跨声轴流压气机转子是典型的高速轴流压气机，其内部复杂流动十分明显，如叶尖间隙流动、角区分离流动、激波与涡相互干涉现象。曾作为叶轮机械领域CFD代码测试的盲题算例之一[10]，该转子的基本设计参数见表1。

根据文献[9]中的稳定性模型预测结果，该转子的失速工况的流量为19.37 kg/s，相对转子转频的失稳频率为86.5%。通常的定常CFD计算在该工况点能够得到收敛解而并不会数值发散达到计算中的失速边界，但是若在进口处加入该频率的畸变扰动则易引起压气机内失速。为了验证该观点，设置了4组不同进口旋转畸变频率的算例，具体参数见表2。

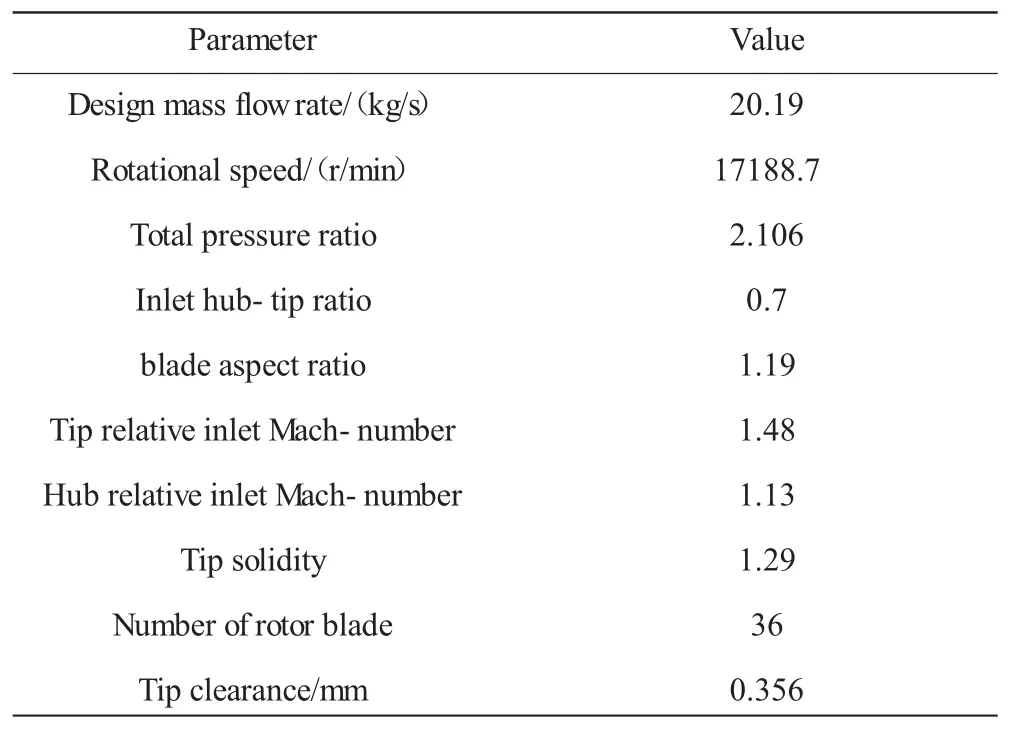
表1 Rotor37基本设计参数

表2 不同进口旋转畸变频率参数

由于在稳定性模型预测结果中无法计算出畸变相对于原本进口参数的变化幅值大小，因此本文畸变的最大幅值统一为进口总压5%。

1.2 数值方法

采用商业软件Fluent进行3维RANS方程的定常以及非定常计算。根据柳阳威[11]、段真真[12]等人的研究成果，湍流模型采用S-A一方程模型，求解器使用有限体积法，离散格式采用1阶迎风隐式格式，压力-速度耦合采用SIMPLEC算法。非定常计算以定常计算结果为初场，采用1阶隐式时间推进法，其中每个叶片通道计算30个物理时间步，其中每个物理时间步包含30个虚拟时间步。

图1 压气机全环通道网格的拓扑结构

计算网格采用商业软件Numeca的IGG模块生成的分块结构网格，由于需要验证的进口畸变周向范围覆盖0～2π的范围，所以本文采用全环通道网格来完整反映进口畸变的影响，其拓扑结构如图1所示。每个转子通道都由7个网格块组成，通道内部和叶顶间隙分别采用O4H型、H-O型网格。虽然较为密集的网格能够更好地反映流场的细节，但是所需计算周期也较长。为了平衡该矛盾，并通过网格无关性验证，最终使用的网格流向、单通道展向和主流径向的节点数分别为105、25和49，其中间隙内的径向分布13个节点，总网格节点数约为600万。所有的固壁面均经过加密处理。

为了使来流充分，计算域的进、出口分别取在距离转子前缘、尾缘约1.5倍弦长处的位置。定常计算的进口边界条件为均匀的轴向进气，进口处的总压、总温分别为101325 Pa、288.2 K；出口为压力出口边界，在半径最小的位置给定静压值，按照径向平衡方程给定出口其他位置静压分布，固壁面采用绝热无滑移边界。在定常计算中通过调整出口静压逐渐逼近预测失速点（m=19.37 kg/s）得到该工况下的定常收敛结果，以此为初场进行非定常计算。在非定常计算中，使用Fluent软件的UDF功能，只改动进口边界的总压分布，使其在进口边界上呈1个完整的正弦分布并且按照一定的转速匀速旋转。进口总压的计算公式为

式中：Pt为总压，下标0代表进口边界；δ为需要计算畸变的幅值，本文中δ=0.05；θ为进口边界上的周向方位角；f为计算畸变旋转的频率，即表2中的变量；t为计算过程中的物理时间。

2 计算结果分析

2.1 定常计算与试验结果对比

根据上述关于定常计算提高出口压力的方法，可以得到完整的压气机压升特性与绝热效率特性曲线，与Dunham[13]给出的试验结果对比，如图2所示。从图中可见，数值模拟能够较好地体现Rotor 37的定常工况曲线的分布规律及趋势。但是与许多文献中的计算结果相同，从绝热效率特性对比图中可见，计算值较试验结果偏低；并且在该计算中得到的数值 发 散 点（m=18.4 kg/s）仍然比试验结果的失速点（19.4 kg/s）略小，证明利用简单的数值发散法用于判断压气机是否进入失速存在较大误差。

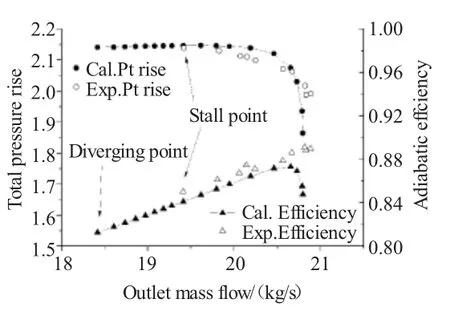
图2 Rotor 37压气机运行工况曲线

为了能够更好地区分流场中的涡结构，本文采用Q法则[14]判断其存在位置。Q值的计算公式为

计算得到的Q值的最大值为涡核的位置。

选取稳定性模型预测失速点（m=19.37 kg/s）处定常计算结果并观察流场中的结构。机匣处壁面静压分布以及极限流线1、通道内靠近叶尖间隙位置的流线2以及通道内沿垂直于流向方向上截面上的Q值分布3如图3所示。从图中可见，虽然在该点处定常计算能够得到稳定收敛的结果，但是从机匣壁面处的静压分布以及极限流线可见，此时叶片通道内已经有明显的尾缘反流现象，但是并没有冲出叶片通道的范围，而是在前缘附近与叶尖间隙泄漏涡掺混而保持较为稳定的形式。

图3 预测失速点定常计算流场

2.2 不同畸变旋转速度计算结果对比

为了观测到失速的发生以及描述失速团的运动规律，本文的算例在通道内距机匣约5%叶高，距转子叶片前缘约1%弦长靠近叶片前缘处沿周向均匀分布了4个数值探针，在相对坐标系下捕捉流场的轴向速度信号，同时在计算过程中监控压气机出口流量的变化。Cal.1与Cal.4的监控结果如图4所示。从图中可见，轴向速度信号的扰动传播速度已完成从相对速度到绝对速度的换算。

从图4（a）、（c）中可见，2个算例在经过约4个转子周期后，出口流量逐渐趋于并维持平稳。从图4（b）、（d）中可见，在叶片前缘附近由于进口的旋转畸变影响存在非定常扰动，同样在较短的时间内（2～3个转子周期）发展为稳定的周期性扰动，并且扰动信号与进口畸变的频率相同。

Cal.2与Cal.3算例的监控结果如图5所示。二者都发生明显的失速现象。

图4 Cal.1与Cal.4算例监控结果

图5 Cal.2与Cal.3算例监控结果

从图中可见，2个算例的出口流量都经过了2个阶段的变化，以Cal.2算例的出口流量图5（a）为例，从0时刻引入进口畸变之后，流量开始减小，但此时减小的趋势并不严重，流量变化曲线斜率并不大；但是在经过约1.2～1.3个转子周期之后，其减小趋势陡然增加，斜率突然增大，可在图5（b）中观察到在第2个数值探针处1个速度剧烈变化的信号，在该信号发生之后压气机内部的流动结构失去稳定性，进入失速工况。该信号沿周向传播的速度约是转子转频的67.3%。Cal.3与Cal.2的计算结果基本一致，失速的信号频率为66.89%，二者在数值上非常接近，稍有不同的是二者信号的产生时间，在Cal.3中失速信号产生的时间约为1.5个转子周期左右。

2.3 Cal.2算例失速机理分析

根据以上分析，约1.2～1.3个转子周期左右产生失速信号，因此选取以下4个瞬时时刻对失速机理进行进一步分析，分别是 t0=0.25T，t1=1T，t2=1.08T，t3=1.2T。4个时刻在压气机内叶片前缘处轴向截面熵的分布如图6所示。

图6 t0、t1、t2、t3时刻叶片通道内熵分布

从图中可见，在刚引入进口畸变不久的t0时刻，叶片通道内部并没有出现明显的高熵区，但是在t1时刻叶尖处发现了熵增区域，对比同一时刻的熵分布，得出在前缘位置出现的高熵区的熵增最大，证明该附近流体能量损失最为严重，随着轴向距离向尾缘推移，高熵区的影响范围先扩大而后逐渐减小。经过一段时间的发展，在t2和t3时刻，熵增区域的范围越来越大并且能量损失也越来越严重。可以认为，正是该低能流体团破坏压气机内部流动稳定性，从而进入失速工况。在定常计算预测失速点、t0、t1以及t2时刻的全展向，部分通道的98%、50%以及5%叶高上的相对马赫数的分布如图7所示。

不同叶高S1流面相对马赫数分布如图7所示。图7（a）中的定常计算结果表明，在98%叶高位置的S1流面通道内存在1个较小的低速团，所处正是在上述分析过的叶尖泄漏涡存在的位置，可以认为该低速团正是叶尖间隙泄漏涡造成的，而随着时间的推移，在叶中（50%）和叶根（5%）位置的S1流面始终没有在叶片通道内出现明显的低速团，而是在尾缘后存在1个由转子叶片的尾流形成的长条形低速区域；而从图7（b）中的t0时刻开始，处于叶尖位置的低速区域面积明显扩大；在图7（c）中t1时刻低速区域已经充满了整个叶尖附近的叶片通道形成堵塞，并且分裂成为2部分的趋势；到了图7（d）t2时刻，压气机由于堵塞流量减小得非常快，叶片前的来流速度降低，通道内的低速区域影响范围已经扩大到通道外区域。从图中该低速团开始明显扩大的时间t1与该区域移动的方向、速度来看，与图5中出现的失速信号特征一致，旋转方向与压气机转向相反，转频为压气机的67%，证明该区域正是流场中出现的失速团。该结论符合目前许多研究学者认为“压气机旋转失速首发于叶片叶尖间隙处”[12，15-16]的理论。

图7 不同叶高S1流面相对马赫数分布

4个时刻的机匣壁面极限流线、静压分布（1）、叶尖间隙附近流线图（2）以及通道内Q值（3）的分布如图8、9所示。

图8 t0与t1时刻流场信息

图9 t2与t3时刻流场信息

从图8（a）中可见，由于此时压气机已经处于近失速工况，所以在机匣表面的极限流线上能够观察到明显的叶尖间隙泄漏涡（TLV）的发展以及尾缘倒流现象，对通道内的流动造成了一定的堵塞。该扰动引入压气机不久，叶片通道内的流动比较稳定，但是畸变在进口位置的低压区仍然在对应通道内形成了较强的逆压梯度。经过一段时间的发展到t1时刻，此时低压区的影响区域已经沿着压气机旋转的反方向传播过了若干个叶片通道，但是可以从静压分布中看出，该区域的旋转速度与进口畸变的旋转速度明显不同。如图8（b）中的Q值分布在前缘附近出现了2种新的涡结构，通过对比2个时刻的壁面静压分布以及极限流线可知，位于吸力面一侧的涡结构为叶尖泄漏涡向前缘推移的结果；根据该处叶尖流线可知，位于压力面一侧的，在跨过叶尖前缘附近的流体中有一部分绕过叶片前缘进入相邻通道，根据李清鹏等[17-19]的研究成果，该流动现象为前缘溢流，进入相邻叶片通道内的溢流会对通道内的流动造成一定程度的堵塞。

图9（c）表示t2时刻的流场信息，此时位于叶片前缘的泄漏涡已经开始脱离，并且由于仍然受到一定程度的进口畸变的低压影响，通道内存在的较强的逆压梯度使得叶片通道波开始向通道外推移；同时尾缘倒流、前缘溢流在图中黑色圆圈位置开始掺混进而产生了一定程度的相互影响，使得流动结构混乱，加大了此处流动能量的损失；同时叶尖间隙泄漏涡破碎，影响范围逐渐扩至整个叶片通道的周向范围。图9（d）表示t3时刻，此时叶片通道内的流场已经发生了不可逆转的破坏，叶片前缘溢流和尾缘倒流的相互作用使得前缘附近产生了复杂的涡流动结构，并且通道波的影响已经完全推出前缘范围，从而在叶片前缘前形成了1个相对高压区域，正是在前文失速信号图中捕捉到的突变失速高压信号。同时也符合Vo等[20]的研究理论，在流场中同时出现前缘溢流及尾缘倒流，压气机出现的失速信号应当是尖峰型信号。

2.4 叶尖位置涡流动破碎过程分析

为了进一步寻找叶尖泄漏涡的破碎与失速信号之间的联系，本文将深入分析叶尖泄漏涡的破碎过程，其非定常发展过程，如图10～12所示。绝对涡量定义为

式中：|ξ|为涡量的模，ω为转子角速度大小，绝对涡量值非常大的区域代表涡核的存在。

每一时刻对应的叶片通道与图8、9的位置相同。在t0时刻，泄漏涡在径向方向的影响范围仅存在于叶尖间隙附近，从图中的流线走势可见，此时通道内从左叶片的吸力面叶尖附近产生的叶尖泄漏涡虽然受到了低压畸变区域的影响，但是仍然保持与定常计算结果中相同的位置与形状，同时通道右侧叶片的压力面由于对进口来流的“推挤”使得流体受离心力的作用沿叶片向机匣位置移动，流动到间隙处时一部分流体跨过间隙形成相邻通道内的叶尖间隙泄漏涡，而另一部分沿相反方向流动最终与通道内的泄漏涡混合在一起。当流场发展到图11中的t1时刻时，可以看到该通道内存在的叶尖间隙泄漏流由于受到左叶片压力面“推挤”过来的流体以及尾缘处产生的尾缘反流的作用，跨过了叶片前缘形成前缘反流（图中黑色圆圈内），并且可见在该时刻泄漏涡影响的径向范围有明显扩张。此时叶片吸力面40%轴向弦长附近原本存在的高绝对涡量区域消失，取而代之的是范围非常大的中、低值绝对涡量区域（如图中红色圆圈区域内所示）。根据Zhang等[21]的理论，该区域发生了泄漏涡的破碎。当发展到图12中的t2时刻时，破碎后的泄漏流在相邻叶片的压力面附近重新产生了绝对涡量较高的区域（如图中黑色圆圈区域所示），这部分涡流动有文献中称之为叶尖泄漏 2 次涡[18-19]（TSV），破碎之后的泄漏涡与相邻叶片的前缘溢流掺混从而在叶尖前缘位置造成堵塞，形成了前文中计算处的失速信号。

图10 t0时刻通道内绝对涡量分布（与图8（a）中同一通道）

图11 t1时刻通道内绝对涡量分布（与图8（b）中同一通道）

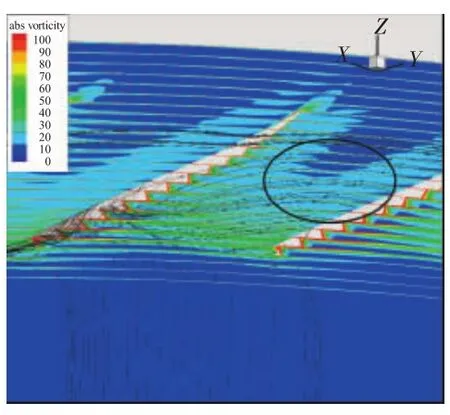
图12 t2时刻通道内绝对涡量分布（与图8（c）中同一通道）

2.5 旋转进口畸变与失速发生的内在联系

目前关于旋转进口畸变与失速发生与否的内在机理的研究尚无定论，张靖煊等[22]认为在压气机进口引入部分位置的旋转畸变，在低压畸变区域首先形成了，与本文的计算结果一致。在流场的非畸变区域观察到了高压区对于该流动不稳定区域有一定的“阻尼”作用。结合本次计算中都未发生失速的结果可以推断：对于不同旋转频率的畸变，初始都会有低压区造成的畸变影响区域存在，但是根据旋转速度的不同，例如Ca.1与Cal.4算例在低压区域形成时进口的高压区域就旋转到了畸变区域从而对流动的不稳定性形成了一定的遏制作用。而对于Cal.2与Cal.3算例，畸变区域没有能够得到高压区域的遏制作用就已经完全失去了稳定性，甚至进口的畸变区还会在一定程度上跟随流动不稳定区域旋转从而加速失速的发生，这也能够解释Cal.2比Cal.3算例要早进入失速工况，因为不稳定流动区域的旋转速度约为67%转频，而Cal.2算例的进口畸变转速与这一值相近。综上所述，最易引起该跨声转子进入失速工况的进口畸变相对转频可能并不是文献[9]中计算的86.5%，而是偏向于67%左右的频率。具体的验证待今后的工作中予以完成。

3 结论

结合目前的研究成果分析了进口旋转畸变与失速的关联性，当畸变转速与压气机内产生的周向传播失稳流体团速度相近时，畸变能够引起旋转失速的发生；反之进口存在的高压畸变区反而会对失稳区域形成一定的遏制作用从而阻止失速的发生。

[1]陈懋章.风扇/压气机技术发展和对今后工作的建议 [J].航空动力学报，2002，17（1）：1-15. CHEN Maozhang.Development of fan/compressor techniques and suggestions on further researches[J].Journal of Aerospace Power，2002，17（1）：1-15.（in Chinese）

[2]Nenni J P，Ludwig G R.A theory to predict the inception of rotating stall in axial flow compressors[C]//AIAA 7th Fluid and Plasma Dynamics Conference.Palo Alto，California：American Institute of Aeronautics and Astronautics,1974.

[3]Greitzer E M.Surge and rotating stall in axial flow compressors-Part I：theoretical compression system model[J].Journal of Engineering For Power，1976，98：190-198.

[4]Greitzer E M.Surge and rotating stall in axial flow compressors-PartⅡ：experimental results and comparison with theory[J].Journal of Engineering for power，1976，98：199-217.

[5]Moore F K，Greitzer E M.A theory of post-stall transients in axial compression systems-Part I：development of equations[J].Journal of Engineering for Gas Turbines and Power，1986 108（1）：68-76.

[6]Greitzer E M，Moore F K.A theory of post-stall transients in axial compression systems-PartⅡ：application[J].Journal of Engineering for Gas Turbines and Power，1986，108（2）：231-239.

[7]Sun X F.Three-dimensional compressible flow stability theory of rotating stall[D].Beijing：Beihang University，1996.

[8]Sun X F.On the relation between the inception of rotating stall and casing treatment[C]//32nd ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.Lake Buena Vista,FL：American Institute of Aeronautics and Astronautics,1996.

[9]Sun X F，Liu X H，Hou R W.A general theory of flow-instability inception in turbomachinery[J].AIAA Journal，2013，51（7）：1675-1687.

[10]Strazisr A J，Denton J D.CFD code assessment in turbomachinery-a progress report[J].Global Gas Turbine News，1995，35（2）：12-14.

[11]Liu Y W，Yu X J，Liu B J.Turbulence models assessment for largescale tip vortices in an axial compressor rotor[J].Journal of Propulsion and Power，2008，24（1）：15-25.

[12]段真真，柳阳威，陆利蓬.周向槽机匣处理对某跨音转子性能影响的数值研究[J].航空学报，2014，35（8）：2163-2173. DUAN Zhenzhen，LIU Yangwei，LU Lipeng.Numerical investigation of the influence of circumferential casing grooves on transonic compressor rotor performance[J].2014，35（8）：2163-2173.（in Chinese）

[13]Dunham J.CFD validation for propulsion system components[R].AGARD-AR-2355，1998.

[14]Zhang S，Choudhury D.Eigen helicity density，a new vortex identification scheme and its application in accelerated inhomogeneous flows[J].Physics of Fluid，2006，18（5）：058104.

[15]Adamczyk J J，Celestina M L，Greitzer E M.The role of tip clearance in high-speed fan stall[J].Journal of Turbomachinery，1993，115（1）：28-39.

[16]SuderK L，CelestinaM L.Experimentaland computational investigation of the tip clearance flow in a transonic axial compressor rotor[J].Journal of Turbomachinery，1996，118（2）：218-229.

[17]Wu Y H，Li Q P，Tian J T.Investigation of pre-stall behavior in an axial compressor rotor-Part I：unsteadiness of tip clearance flow[J]. Journal of Turbomachinery，2012，134（5）：597-608.

[18]Wu Y H，Li Q P，Tian J T.Investigation of pre-stall behavior in an axial compressor rotor-Part II：flow mechanism of spike emergence[J]. Journal of Turbomachinery，2012，134（5）：609-626.

[19]吴艳辉，李清鹏，楚武利，等.亚声速压气机转子失速先找诱发机制的非定常机理分析 [J].西北工业大学学报，2011，29（3）：491-496. WU Yanhui，LI Qingpeng，CHU Wuli，et al.Unsteady flow mechanism of spike emergence in a subsonic axial flow compressor rotor[J]. JournalofNorthwestern PolytechnicalUniversity，2011，29（3）：491-496.（in Chinese）

[20]Vo H D，Tan C S，Greitzer E M.Criteria for spike initiated rotating stall[J].Journal of Turbomachinery，2008，130：1-9.

[21]Zhang Y F，Lu X G，Chu W L，et al.Numerical investigation of the unsteady tip leakage flow and rotating stall inception in a transonic compressor[J].Journal of Thermal Science，2010，19（4）：310-317.

[22]张靖煊，林峰，陈静宜，等.旋转进口畸变条件下轴流压气机叶顶间隙流非定常特征及其与旋转失速的关联性研究[J].工程热物理学报，2008，29（3）：390-394. ZHANG Jingxuan，LIN Feng，CHEN Jingyi，et al.The unsteady features and role of tip clearance flow in distortion induced instability in an axial compressor[J].Journal of Engineering Thermophysics，2008，29（3）：390-394.（in Chinese）

（编辑：肖磊）

Numerical Investigation for Stability Influences of Rotating Inlet Distortion Frequency on a Transonic Compressor

XIE Zhe1，2，LIU Yang-wei1，2，LIU Xiao-hua1，2，SUN Xiao-feng1，2，LU Li-peng1，2
（1.National Key Laboratory of Science and Technology on Aeroengine Aerothermodynamics，Beihang University，Beijing 100191，China;2.Collaborative Innovation Center of Advanced Aeroengine，Beijing 100191，China）

In order to investigate the effect of rotating inlet distortion on compressor stall process,and discuss the existence of a specific disturbance frequency（Eigen frequency）which is easy to induce the rotating stall，the effect of four kinds of different inlet rotating frequencies on the Rotor 37 stall process of a transonic compressor was calculated and investigated by the unsteady numerical simulation methods.The results show that when the rotating frequency is similar to the stall disturbance frequency,the inlet distortion frequency could cause the rotating stall on the same amplitude condition,while the compressor rotating grows into stable when the frequencies in different values.After the low pressure district of inlet distortion lead to flow structure in parts of the blade passage destabilization,the breakdown of tip leakage vortex developed into blockage and induced the existence of rotating stall.The developing procedure of stall cell in the rotor is well described and the mechanism influence of inlet distortion frequency on the stall process is obtained by the method.

inlet distortion；rotating stall；disturbance frequency；tip leakage；transonic compressor；stability；numerical simulation

V 231.3

A

10.13477/j.cnki.aeroengine.2015.05.001

2014-11-21 基金项目：国家自然科学基金（51420105008、51376001、51406229）、民口973（2012CB720205）、航空科学基金（2012ZB51014）、北京高等学校青年英才计划项目资助

谢喆（1989），男，硕士，主要研究方向为压气机稳定性；E-mail：xiezhe890917@126.com。

谢喆，柳阳威，刘小华，等.旋转进口畸变频率对跨声速压气机稳定性影响的数值研究[J].航空发动机，2014，41（5）：1- 7. XIE Zhe，LIU Yangwei，LIU Xiaohua，et al.Numerical investigation for stability influences ofrotatinginlet distortion frequencyon a transonic compressor[J].Aeroengine，2014，41（5）：1- 7.