一种弹载永磁同步电机的综合物理场计算

李 鹏，王佳民，王 卿，胡锦垚

(中国航天科技集团十六研究所，西安710100)

0 引 言

永磁同步电动机具有结构简单、体积小、重量轻、损耗小、效率高、转矩波动小等特点，因而其应用领域越来越广。弹载设备中对体积的严格限制，并且环境条件要求十分苛刻，而且对于动力输出设备，其驱动力必须充足稳定，所以该弹载永磁同步电机设计及制造具有一定的难度。本文首先通过磁路计算法确定电机的关键部分尺寸，然后利用电磁场有限元仿真软件Ansoft，建立适当的参数化模型，对电机电磁特性进行计算并对设计参数进行优化，再采用ANSYS 对电机温度场进行计算，最后制造样机对电机优化及仿真计算结果进行验证。

1 结构设计

1.1 设计要求

电机外形尺寸要求不大于Φ55 mm×70 mm，性能指标:额定功率600 W ，额定电压270 V，额定电流要求小于3 A，额定转速13 000 r/min，额定转矩0.44 N·m，电机最高工作环境温度120℃。

1.2 关键尺寸选定

电动机的尺寸对电动机的性能起着决定性作用，它直接影响着电动机的转矩、功率、转速等重要性能。当电动机的功率和额定转速以及电动机的电磁负荷确定以后，电动机的主要尺寸——定子铁心内径Di1及其轴向长度L1就可以根据下式来确定［1-5］:

1.3 结构设计结果

经过反复计算，最终选取电机机构各部分尺寸参数如表1 所示。

表1 主要结构尺寸

最终在上述所选结构尺寸情况下计算得出电机关键部分平均磁场密度，如表2 所示。

表2 关键部位磁场密度

2 有限元分析

在磁路法设计得到电机各部分结构参数的基础上建立电机几何模型，然后分别对电机进行电磁场和温度场有限元分析。

并利用电磁场有限元仿真软件Ansoft 对电机电磁场进行分析计算，对于温度场的计算，本文采用ANSYS 进行计算。

2.1 电磁场分析

对电机电磁场的分析采用二维电磁场分析，利用电磁场有限元仿真软件Ansoft 对电机电磁场进行分析计算［6］。

2.1.1 电磁场有限元模型的建立

在用有限元法分析电磁场时，常引入矢量磁位Az作为求解变量，并对忽略交变磁场在电机定子和转子铁心中的涡流反应，于是结合麦克斯韦(Maxwell)方程组可得到电机电磁场计算的基本数学方程［7］:

式中:Jz为沿电机轴向的电流密度;Γ1为第一类边界条件;Γ2为第二类边界条件;A0为矢量磁位边界值;Hτ为磁场强度的切向分量;μ 为磁导率。

2.1.2 气隙磁密计算

在Ansoft 中为建立的电机几何模型各部分设置相应的材料，并设定电磁场计算的边界条件，静态磁场仿真可得到电机的磁力线和磁密云图如图1 所示。在图1 中可看出静态磁场强度最大值为1.72 T，各关键部位的平均磁密与磁路计算结果相吻合。

图1 磁力线和磁密云图

为了观测定子齿槽对气隙磁密波形的影响，在此特意建立一个无齿槽的定子，进行静态磁场计算，得到无齿槽时的气隙磁密波形，与有齿槽时气隙磁密波形的对比情况如图2 所示。再分别对有齿槽和无齿槽时的气隙磁密波形进行傅里叶分解，得到其频谱如图3 所示。从图3 中可看出有齿槽时和无齿槽时频谱图相差不大，这在一定程度上反映了极槽数选取较为合理。

2.1.3 反电势计算

相反电势如图4 所示。齿槽转矩如图5 所示。

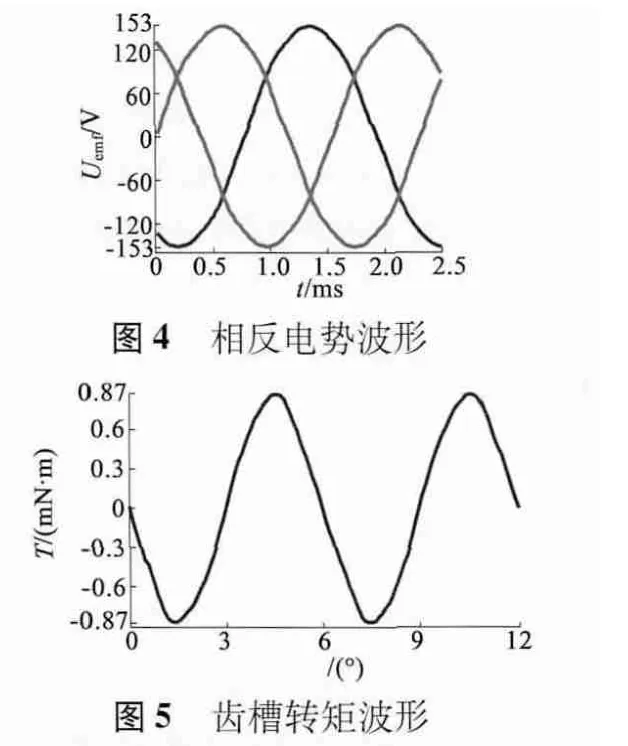
2.1.4 齿槽转矩和电磁转矩计算

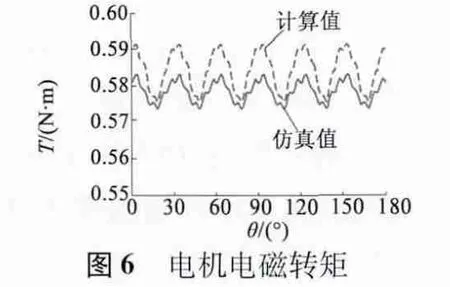
假设电机在额定状态下运行时相电流有效值为2.44 A，当给电机三相绕组中通以三相正弦交流电，通过调整电流初始相位，使电机电流只产生交轴磁场，其中电流的有效值为2.44 A，仿真得出此时电机的电磁转矩，再通过电机瞬时反电势和电流以及在特定位置处的齿槽转矩，可粗略计算出电机的瞬时转矩，并与仿真值相对比，结果如图6 所示。从图6 中可看出，计算值明显大于仿真值，这是因为计算值是建立在电机无铁耗的基础上。仔细观察可发现，计算值与仿真值都以30°机械角度为周期波动，这是由反电势中幅值较高的七次谐波引起的，以60°电角度为周期的正弦波动与其他高次谐波引起波动的及齿槽转矩的总和。观察还可发现，齿槽转矩幅值相对于转矩波动相差约一个数量级，对转矩波动影响较小，故不把齿槽转矩作为优化考虑的因素。

2.2 温度场计算

对于电机温度场的计算分析，采用三维温度场进行计算分析，本文采用ANSYS 软件进行计算。

2.2.1 温度场有限元模型的建立

首先在Pro/E 中绘制出电机各零件的零件图，然后把各零件按一定的顺序组装起来，完成电机的三维模型，接下来把电机的三维模型导入ANSYS 软件进行温度计算［10］。

为简化计算，此处对电机模型进行以下简化:将同一槽内的绕组简化为一根铜条;将电机铜耗和铁耗视为分别均匀分布于导线和铁心中;认为电机机壳各外表面的换热系数值相等;把电机气隙内的对流换热等效处理为与导热系数大于空气的材料的热传导。

根据三维有限元和传热学基本理论，可得三维稳态温度场的基本数学方程［8-9］:

式中:T 为节点温度;λx，λy，λz为各方向上的导热系数;λn为沿热流方向的导热系数;q 为热源的产热密度;h 为对流换热系数;t 和t0分别为物体表面温度和流体温度;s1为等温面;s2为对流换热面。

在进行计算之前首先查阅相关材料的导热系数、比热容和密度等参数，并分别为电机模型中各部分材料输入相关参数。

2.2.2 温升计算

温升测试时，电机安装在体积较大的钢材料实验台上，此处假设电机机壳安装接触面温度为一恒定值，仿真得到电机额定工作状态下铁心损耗约为22 W，绕组铜耗约为52 W，其余条件与空载情况下状态相同。计算结果整体效果如图7 所示。

从计算结果中可以看出，机壳表面最高温度约为81.6℃，而电机最高温度约为82.4℃，电机最高温度位于绕组上，结果如图8 所示。仿真计算结果表明电机在负载状态下运行时温升约为60℃，则当电机工作环境温度上升到120℃时，其绝缘结构和磁钢必需要承受180℃左右的高温，则绝缘结构材料的耐热等级必需选用H 级及以上等级，才能保证电机在120℃的高温工作环境下可靠运行，而磁钢材料选为钐钴永磁合金，完全可以承受180℃的高温。

图7 负载温升整体效果

图8 负载温升图(电机内部)

3 电机优化设计

本文仅对电机的磁钢极弧系数和绕组匝数两项设计参数进行最优化设计，通过调整极弧系数，使电机气隙磁密波形形达到最接近正弦波的状态;通过调整绕组匝数，使电机的最高转速达到设计要求，从而使电机的性能达到与设计要求最接近的状态。

嘉善田歌，作为我国一种原生态歌唱艺术和一项音乐类非物质文化遗产，也面临自然界“物种锐减濒危”的考验。在一份关于嘉善田歌认知度调查报告中显示，在当地虽被80%受访者所知，但只有不足4%会唱[1]。可见嘉善田歌在大众生活中已渐行渐远，面临着失传危机，保护它可谓是任重而道远。通过对田歌的活态现状、生存环境和价值进行调研和分析，就嘉善田歌如何在全球单一化、科技一体化、网络信息化和经济高速化大背景下传承发展进行了一些整理和思考。

3.1 极弧系数优化

极弧系数的大小会直接影响气隙磁密的波形宽度，进而影响到主磁通的大小以及电机各部分的磁密大小，最终影响整个电机的力能指标。因此必需对极弧系数进行优化，调节电机磁路磁通大小，使电机有较好的工作状态。通过参数化建模，选择适当的参数，本文把每片磁钢圆弧对应的圆心角设置为模型参数，便于对极弧系数进行优化。例如本文对每片磁钢圆弧对应的圆心角从60°以1°为步长取到80°，并对其气隙磁密进行仿真计算，并分析气隙磁密的频谱特性，气隙磁密波形如图9 所示，从图9 中可以看出，随着磁钢极弧角度的增大，其气隙磁密波形的宽度不断增加，各个波形的频谱特性如图10 所示。

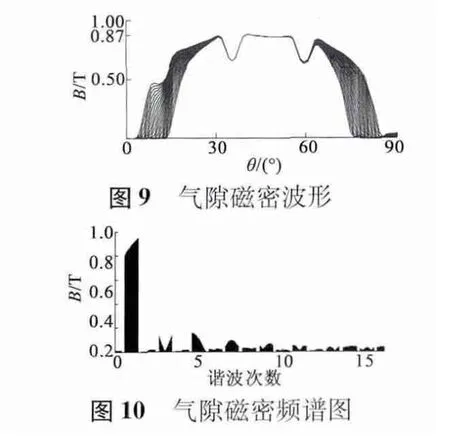
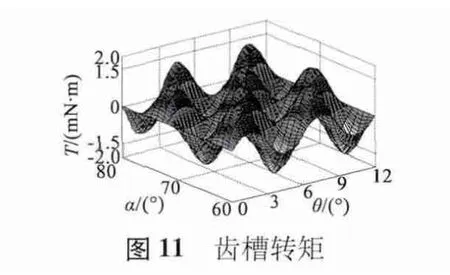
然后对其齿槽转矩进行仿真分析，其结果如图11 所示。从图11 中可看出，当极弧角度选取为特定值时齿槽转矩的幅值可以取到最小值，齿槽转矩最大幅值在1.5 mN·m 左右，对应的极弧角度约为62°，68°和74°;齿槽转矩最小值在0.065 mN·m 左右，对应的极弧角度约为77°，71.3°和65.3°。

最后对其反电势进行仿真，其相反电势幅值随极弧角度的变化从140 V 逐渐增加到164 V，随后对反电势进行频谱分析并计算谐波失真度(除基波外的所有次谐波的方均根值的方和根与基波方均根值之比):

式中:φv表示反电势中的v 次谐波的方根均值。本文只计算了前50 次谐波，结果如图12 所示。极弧角度从60°逐渐增加到80°的过程中，反电势的谐波失真度在1.5% ～2.0%之间变化。可看出，在此极槽数配合使用的结构中，磁钢极弧角度对反电势波形的谐波失真度影响较小，则可根据其他性能要求选择磁钢极弧角度，如凸极效应要求、转子铁心工艺性和机械强度要求、电机各部分磁密要求、永磁体的用量要求等。

图12 反电势的谐波失真度

电机电磁转矩和极弧角度的关系如图13 所示，从图13 中可看出，随着极弧角度的增加，电磁转矩从0.537 N·m 逐渐增加到0.615 N·m。

图13 电磁转矩和极弧角度对应关系

在优化极弧系数的同时，对空载和负载情况下的关键部位的磁密进行统计，结果如表3 所示。

表3 电机空载和负载状态下各部分磁密

由于电机无位置传感器，电机控制要求电机具有较明显的凸极效应，故在保证电机各部分磁密接近饱和的情况下，电机的磁钢极弧系数最终选取为0.78。

3.2 绕组匝数优化

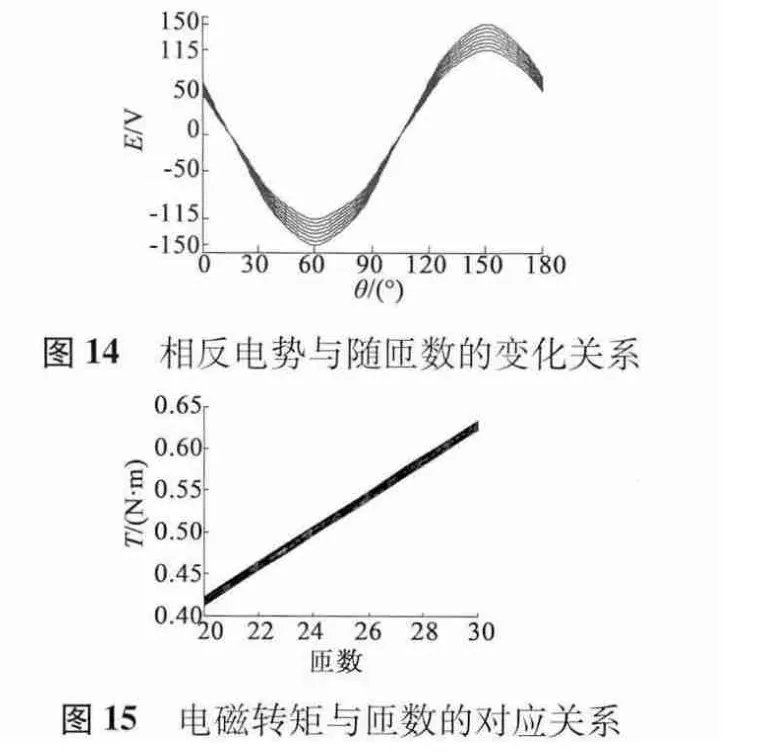
再仿真电机电磁转矩，其结果如图15 所示。从图15 中可看出随着匝数的增加，电磁转矩从0.42 N·m 逐渐增加到0.625 N·m，结合电机额定指标，选取合适的匝数。

4 实验结果

为保证电机样机制造成本控制在一定范围内，样机极弧系数均为0. 78，匝数为25，26，27，28 四种。对样机的测试包括:对拖电机测试反电势，观察反电势波形;在工控机上测试电机在几个关键状态下运行的转速以及输出转矩等参数。

对拖测得其三相反电势波形如图16 所示，计算得到其反电势系数从25 到28 匝分别为0. 155，0.158，0.166，0.175。与仿真结果进行对比可发现，实测值略低于仿真值，分析原因为铁心叠压系数取值不准确。

图16 三相反电势波形图(截图)

电机在最高转速额定负载状态下测试得到的力能指标如表4 所示(表4 中，28 匝的样机测试数据是在电源电压升高到280 V 情况下的测试得出)。

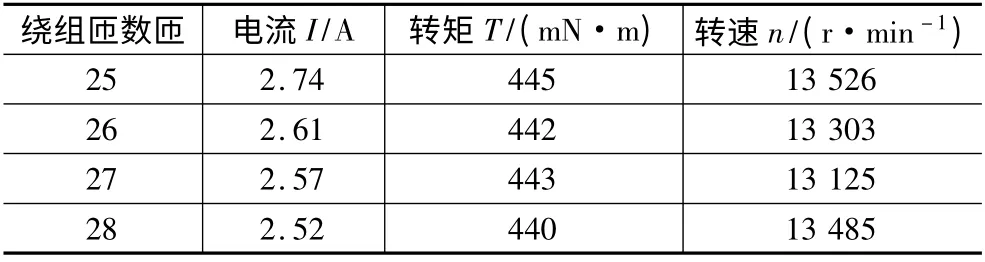
表4 电机最高转速状态

从表4.3 可看出，只有匝数为25 匝的样机，其最高转速可以达到13 500 r/min，匝数为28 匝的样机在电源电压增加到280 V 时，其转速才勉强达到13 500 r/min。综合考虑，为使电机具有较高的裕度，而25 匝的样机在13 526 r/min 转速额定转矩状态下，其控制器输入总电流为2.74 A 小于3 A，符合设计要求，故最终确定电机的匝数为25 匝。

温升测试方案为选用两台规格相同的电机，一个作为电动机，另外一个作为发电机，用电动机拖动发电机转动，发电机输出接到一个散热良好的大功率电阻和一个滑动变阻器串联的电路上，使用滑动变阻器的目的是为了通过调节电路电阻，来调节电路上消耗的功率，改变发电机的工作状态，进而调节电动机对发电机提供的负载转矩，使电动机工作在额定状态下，两台电机均安装在体积较大的钢材料实验台上。

电机运转60 min 后，位于绕组端部的热敏电阻阻值不再变化，记下此时热敏电阻的阻值，根据阻值查得电机绕组端部的温度为83 ℃，与计算值相差较小，验证了电机传热计算的正确性。

5 结 语

本文主要通过电机的设计要求和磁路法计算确定电机的关键尺寸参数，然后用有限元仿真软件Ansoft 对电机进行仿真分析，验证由磁路法确定的参数的合理性，再通过有限元仿真软件对电机各运行状态的磁场和温度场进行仿真计算。然后再通过仿真对极弧系数和绕组匝数进行优化，选取与设计要求指标相近的极弧系数和绕组匝数，最后根据优化分析结果，制造了匝数分别为25 ～28 匝的4 台样机，并对样机的电磁特性和温度特性进行测试，样机测试结果与仿真计算结果基本吻合，验证了仿真计算的正确性。最后根据实际样机的测试结果，最终确定了电机的绕组匝数为25 匝。根据反电势系数计算得出，当电机工作在额定转速下，其线反电势幅值为211 V，额定工作状态下驱动器输入电流为2.545 A ＜3 A，且在额定负载情况下，其最高转速可达到13 500 r/min，使电机转速具有一定的裕度。

［1］ 李钟明，刘卫国.稀土永磁电机［M］. 北京:国防工业出版社，1999.

［2］ 唐任远.现代永磁电机理论与设计［M］. 北京:机械工业出版社，2006.

［3］ 陈世坤.电机设计［M］.北京:机械工业出版社，2005.［4］ 王秀和.永磁电机［M］.北京:中国电力出版社，2007.

［5］ 王琇.基于场路结合的永磁同步电机分析与优化［D］. 杭州:浙江大学，2013.

［6］ 赵博，张洪亮.Ansoft 12 在工程电磁场中的应用［M］.北京:中国水利水电出版社，2010.

［7］ 王玮.永磁电机的设计与分析［D］.南京:南京理工大学，2014.

［8］ 胡淑环.永磁电机热计算研究［D］.沈阳:沈阳工业大学，2009.

［9］ 徐建国.基于有限元温度与结构分析的电机优化与设计［D］.武汉:华中科技大学，2009.

［10］ 李兵，陈雪峰等. ANSYS Workbench 设计、仿真与优化［M］.北京:清华大学出版社，2008.