一种简单的无刷直流电动机转矩脉动抑制方法

荣 军，李一鸣，万军华，张 敏，陈 曦

(1.湖南理工学院，岳阳414006;2.长沙理工大学，长沙410014 )

0 引 言

电磁转矩的大小是判断无刷直流电动机工作性能好坏最重要的一个因素。如果转矩脉动过大，不但缩短电机的工作时间，而且会降低电机的可靠性，最终影响其在各个行业的应用，因此解决无刷直流电动机的转矩脉动一直是众多科研人员努力的方向［1］。根据无刷直流电动机转矩脉动产生的原因不同，它主要分为齿槽转矩脉动和电流换相转矩脉动，对于前者，文献［2］通过采用斜槽法或斜极法，通过改善电机的气隙磁场，从而消除由于齿槽电机本体设计方面产生的电磁转矩。对于后者，由于是电流换相期间电流变化作用所引起的转矩脉动，国内外有许多作者提出了解决办法，比如文献［3］提出重叠换相法，能有效抑制转矩脉动，但是直流电机的参数不好选择，在电机实际应用中较难实现。文献［4］所用的方法是在电流换相期间，适当地增大占空比来抑制转矩脉动，但是在实验过程中，换相期间占空比很难控制，实际上转矩脉动抑制效果不明显。

本文从不同PWM 工作模式对电流换相过程中转矩脉动产生的原因进行深入分析，得出了一种简单而且容易实现的无刷直流电动机转矩脉动抑制方法，详细地推断其工作原理，最后通过实验对其进行了验证。

1 不同PWM 调制模式下换相转矩脉动的产生原因

由无刷直流电动机统一理论可得其电磁转矩数学表达式［5-6］:

式中:TM为电磁转矩;Pe为电磁功率;Ω 为电机机械角频率;ea，eb，ec为三相电枢绕组反电势;ω 为电机转子角频率;p 为电机的极对数。

如果无刷直流电动机工作在二二导通三相六状态的工作期间，任意一个60°工作扇区均只有两相能够导通，其电磁转矩表达式:

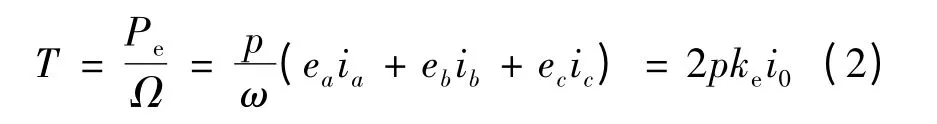
式中:ke为电磁转矩常数;i0为当前电流稳态值。

此时，电磁功率Pc与i0成正比。但实际上，由于电感对电流有阻碍作用，导通相电流不能从零瞬间达到稳态值。类似于导通相电流，关断相电流也不能从稳态值立刻降到零，而需要通过借助续流通道使电流慢慢降到零。因此没参与电流换相的第三相电流大小会发生变化，从而不能一直保持稳态电流，这会导致电磁转矩增大，这就是电流换相产生转矩脉动的重要原因［4，7-8］。

1.1 上桥电流换相时PWM-ON 和HPWM-LON 调制模式下转矩脉动产生的工作原理分析

根据功率开关管上下桥臂调制的不同，将单边调制模式分为上桥换相和下桥换相两种。为了方便研究，先介绍上桥电流换相过程，在上桥电流换相期间，PWM-ON 调制模式和HPWM -LON 调制模式具有相同的续流方式，ON -PWM 调制模式和HON-LPWM 调制模式续流方式类似，因此分开讨论。

假设V1 关断，V3 为PWM 调制，V2 恒通，图1的三相梯形反电动势波形中的2 -3 扇区，A 相电感续流期间电流的工作过程如图2 所示，此时电机系统三相端电压平衡方程:

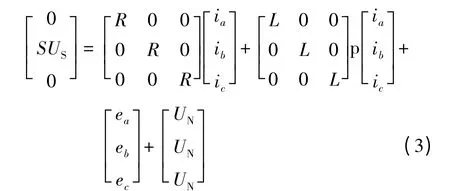
式中:S=0，1 为V3 的开关函数，S =1，V3 导通;S =0，V3 关断;p 为微分算子。

图2 上桥换相时A 相续流期间电流的工作过程一

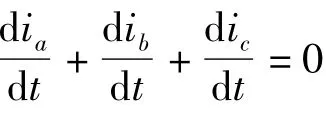
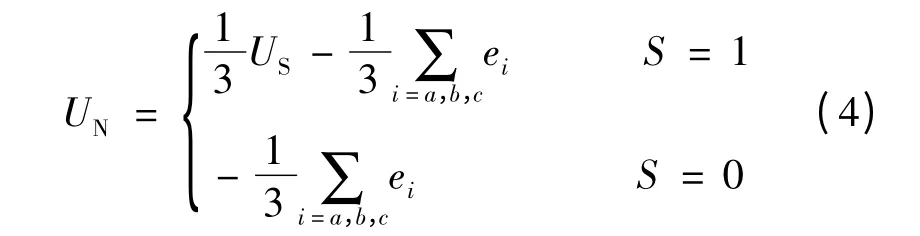
在图1 中的2 -3 扇区，eb= -ec=keω，而ea是一个复杂的斜坡函数，同时其中性点还受PWM 工作方式的影响，所以其表达式非常复杂，不好计算。为了便于描述，作如下简化，假设电流换相期间反电动势保持不变，则ea≈keω，设D 为当前PWM 脉冲占空比，则:

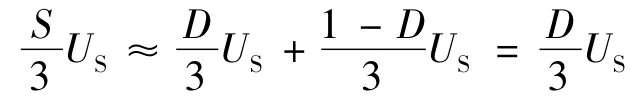
则式(4)可简化:

在上桥换相前，ia(0)= -ic(0)=i0，ib(0)=0，此时将式(5)和式(3)联立，可得电流换相过程中电机系统的三相电流计算表达式:

由式(1)变形可得电流换相过程中电机电磁转矩:

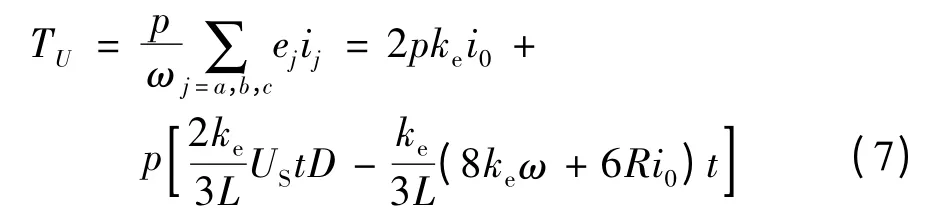
将式(7)与式(2)联立，可得换相转矩脉动的计算公式:

1.2 上桥电流换相时ON-PWM 和HON-LPWM 调制模式下转矩脉动产生的工作原理分析

当V2 为PWM 工作方式时，此时V3 一直保持恒开通，一个开关周期内的电流的工作过程如图3所示。此时在A 相续流导通期间，电机的三相端电压平衡方程［9］:

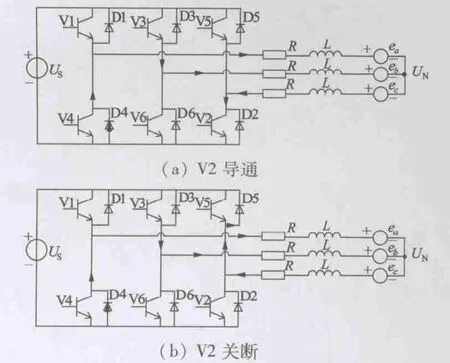
图3 上桥换相时A 相续流期间电流的工作过程二

式中:S=0，1 为V2 的开关函数，S =1，V2 导通;S =0，V2 关断。

由式(5)和式(9)解得:

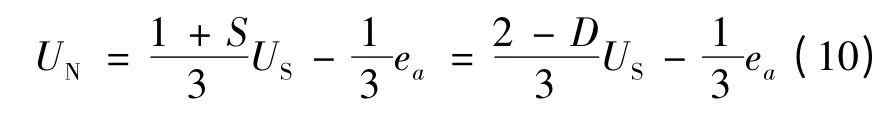
将式(10)与式(9)联立，可得三相电流的计算公式:

此时可得出上桥电流换相过程中的电磁转矩表达式:

如果将式(12)与式(2)联立，可得电流换相过程中的电磁转矩脉动:

将式(8)和式(13)进行对比，可得在两组不同工作情况下，电机电流换相转矩脉动的偏差计算公式:

1.3 下桥电流换相时ON-PWM 和HPWM-LON 调制模式下转矩脉动产生的工作原理分析

与上面的上桥电流换相过程分析类似，在下桥电流换相过程中，同样ON -PWM 调制模式和HPWM-LON 调制模式归为一类;PWM-ON 调制模式和HON-LPWM 调制模式归为一类，原因在于它们的续流过程类似。在分析下桥换相工作原理之前，假设功率管V4 关断，功率管V6 一直保持开通，功率管V5 工作在PWM 调制模式下，此时A 相电感续流期间电流的工作过程如图4 所示。在A 相续流工作期间，电机三相端电压方程［10］:

由式(15)整理得:

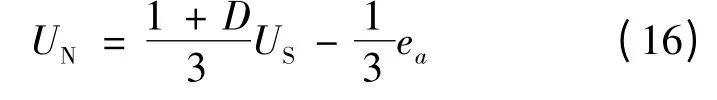
由于在电流换相过程中有:ea≈eb= -ec= -keω和ia(0)= -ic(0)= -i0(0)，因此将式(16)代入式(15)并整理得换相过程中三相电流的计算公式:

在这两种调制方式下，下桥换相过程中的电磁转矩:

联立式(18)与式(2)可计算出电流换相过程中的转矩脉动:

1.4 下桥电流换相时PWM-ON 和HON-LPWM 调制模式下转矩脉动产生的工作原理分析

当V6 为PWM 工作方式时，V5 同样保持恒导通，一个开关周期内的电流工作过程如图5 所示。A相续流过期间，电机的三相端电压方程:

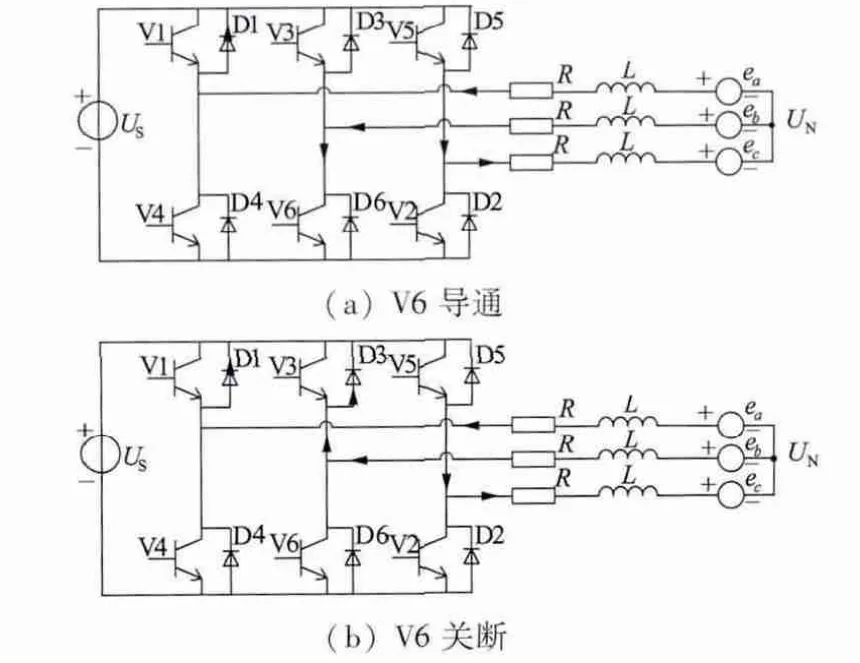
图5 下桥换相时A 相续流期间电流的工作过程二

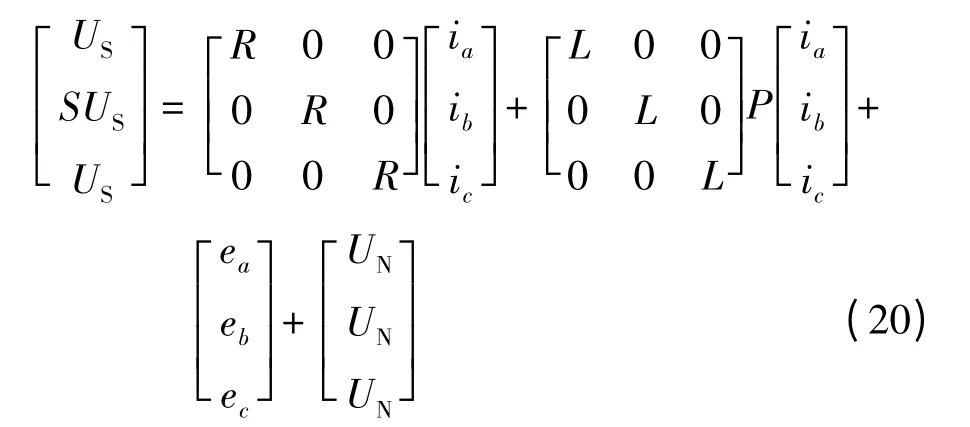
由式(16)和式(20)联立可推出:

将式(21)和式(20)联立可得电流换相过程中电机的三相电流:

此时可得出下桥电流换相期间电磁转矩表达式:

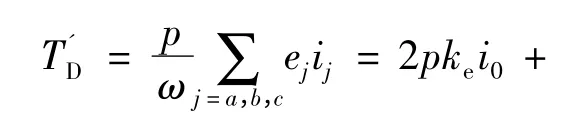
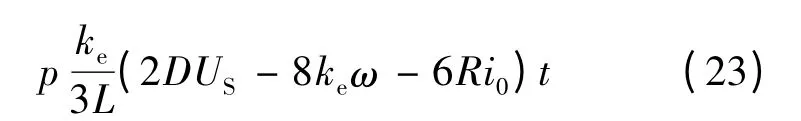
因此，可进一步得出电流换相期间的电磁转矩脉动表达式:

通过上面的理论分析，在上桥电流换相过程中，无刷直流电动机工作在PWM-ON 和HPWM-LON工作模式下，电流换相产生的转矩脉动比ON -PWM 和HON-LPWM 调制模式下要小一些。而在下桥换相过程中，电机工作在PWM -ON 和HON -LPWM 工作模式下，电流换相产生的转矩脉动比工作在ON -PWM 和HPWM -LON 调制模式下要小一些［10］。

2 直接面向转矩脉动的转矩补偿原理介绍

为了消除电流换相产生的转矩脉动，本文研究一种直接面向转矩脉动的转矩补偿方法，这种补偿方法的原理非常简单，就是先建立转矩脉动方程，然后令转矩脉动等于零，基本可以实现消除转矩脉动［11］。为了研究方便，本文就以HPWM - LON 调制模式为例推断其工作原理。在HPWM -LON 调制期间，上桥电流换相产生的转矩脉动为式(8)，此时可令ΔTU=0，即:

如果能够保证在换相期间的任何时刻式(26)均成立，则可得到以下结论:

由式(27)进一步可解得:

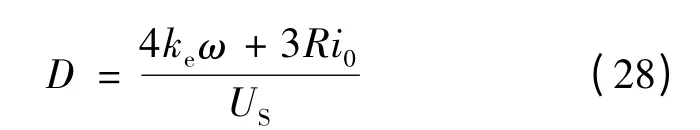
在上桥电流换相结束时，A，B，C 相电流分别为0，i0和-i0。根据式(6)，可解得换相时间tf:

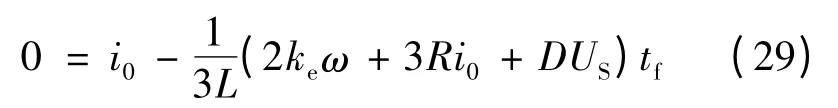
从而最终得出tf的表达式:

此时可以定义上桥电流换相期间所对应的补偿占空比和换相时间分别为Dup和tfup，即:

结论:在上桥换相时，在tfup时间内占空比调整为Dup，能抑制或消除转矩脉动。

下桥换相引起的转矩脉动为式(19)，令ΔTD=0，即:

要使在换相时间内的任何时刻式(33)均成立，则:

解得:

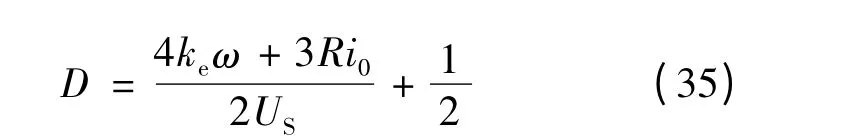
在下桥换相结束时，A，B，C三相电流分别0，-i0和i0。根据式(19)，可解得换相时间tf:

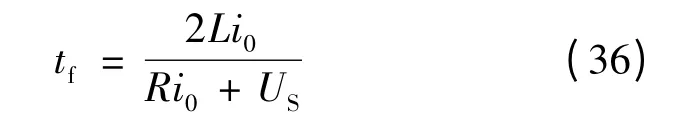
此时可以自定义下桥换相所对应得补偿占空比和换相时间分别为Ddown和tfdown，即:

结论:在下桥电流换相期间，如果能够在tfdown时间内将占空比调整为Ddown，因此就能够实现消除转矩脉动。

3 面向转矩脉动的直接转矩补偿方法的仿真结果及分析

根据以上分析，以HPWM -LON 调制方式恒转速为例进行仿真验证，其仿真结果如图6 ～图8 所示，从图6 实验波形中可以看出，进行转矩脉动补偿后的电枢电流相比补偿前波形变得平滑。从图7 的仿真波形看出，电枢反电动势在补偿前和补偿后没有任何改变，说明进行转矩脉动补充不影响电枢反电势。从图8 的仿真波形可以看出，电机输出功率脉动波形在补偿后比补偿前显著降低，这与无刷直流电动机在转速不变的情况下，输出功率与电磁转矩成正比的关系，因此输出功率脉动的大小直接反映转矩脉动大小这一结论相符合，也直接通过仿真实验证明了通过转矩补偿后，转矩脉动显著降低。

4 结 语

本文根据两相导通三相星形六状态电机工作模式，详细地分析了不同PWM 调制模式对无刷直流电动机电流换相转矩脉动产生的原因。首先根据功率开关管上桥臂和下桥臂工作机理的不同，将无刷直流电动机分为上桥换相和下桥换相分别进行讨论，然后再根据换相时续流过程的不同，将PWM -ON 和HPWM-LON 两种PWM 调制方式归为一类分析，而ON-PWM 和HON -LPWM 两种调制方式归为另外一类考虑，分别推断电机电流换相转矩脉动产生的原因，最后研究了直接面向转矩脉动的转矩脉动补偿方法去消除转矩脉动，并在PSPSIC 中进行了验证，仿真结果证明了理论分析完全正确，为消除无刷直流电动机电流换相时产生的转矩脉动提供了一种简单实用的方法。

［1］ 王俊，毛鹏军，彭中.无刷直流电动机转矩脉动抑制控制方法［J］.微特电机，2007，35(9):39 -41.

［2］ 罗宏浩，吴峻，常文森.动磁式永磁无刷直流直线电机的齿槽力最小化［J］.中国电机工程学报，2007，27(6):12 -16.

［3］ 张殿军. 鱼雷推进用无传感器无刷直流电机动态性能分析［D］.西安:西北工业大学，2007.

［4］ 吴一欣，廖军辉.无刷直流电机转矩脉动抑制研究［J］.计算机仿真，2009，26(10):365 -369.

［5］ 张相军，陈伯时.无刷直流电机控制系统中PWM 调制方式对换相转矩脉动的影响［J］.电机与控制学报，2003，7(2):87 -91.

［6］ 袁林兴.稀土永磁无刷直流鱼雷推进电机控制系统设计研究［D］.西安:西北工业大学，2006.

［7］ 包向华，章跃进.五种PWM 方式对无刷直流电动机换相转矩脉动的分析和比较［J］.中小型电机，2005，32(6):48 -52，55.

［8］ 周美兰，高肇明，吴晓刚，等.五种PWM 方式对直流无刷电机系统换相转矩脉动的影响［J］. 电机与控制学报，2013，17(7):15 -21.

［9］ 齐蓉，林辉，陈明. 无刷直流电机换向转矩脉动分析与抑制［J］.电机与控制学报，2006，10(3):287 -290.

［10］ 贺虎成，刘卫国，郎宝华.永磁无刷直流电动机非换相区间转矩特性研究［J］.电气传动，2007，37(10):33 -38.

［11］ 袁林兴，焦振宏，杨燕，等. 直接面向转矩脉动的转矩补偿方法［J］.微电机，2006，39(4):12 -15.