基于Excel和Pro/E的平面二次包络环面蜗杆造型

付大鹏，孙文杰，王丽乾

(东北电力大学机械工程学院，吉林 吉林 132012)



基于Excel和Pro/E的平面二次包络环面蜗杆造型

付大鹏，孙文杰，王丽乾

(东北电力大学机械工程学院，吉林 吉林 132012)

本文主要介绍了利用Excel求解方程组，并通过Mtalab数值处理方法对其准确性进行验证，再将获得的三维坐标点导入Pro/E获得平面二次包络环面蜗杆三维模型的方法。该方法充分应用了Excel无需大量数据编程即可求解方程组的优点， 以及Pro/E易于掌握的的曲面处理和实体造型的功能，使平面二次包络环面蜗杆的建模更快捷、简便。

Excel和Pro/E；环面蜗杆；三维造型

0 前言

圆弧面蜗杆传动具有多齿啮合、承载能力高、润滑角和诱导法曲率半径大、易于形成动压油膜、磨损小、寿命长、传动平稳等优点，因此对于平面二包环面蜗杆的研究具有相当重要的意义[1]。而其中以平面二次包络环面蜗杆的运用较为普遍，但由于平面二次包络环面蜗杆的成形及啮合原理的特殊性，运用普通的造型方法就很难得到它准确的实体模型。而现代的机械加工皆是在三维模型的基础上，先进行仿真加工，再具体到实物加工[2-3]。所以得到二次包络环面蜗杆的三维模型就显得尤为重要。国内有一些学者运用三维软件的二次开发对平面二次包络环面蜗杆进行三维实体建模，如文献[4]；或运用Matlab进行数值计算再运用三维软件进行实体建模,如文献[5]。但这些方法都必须以熟知计算机编程语言为载体，进行复杂的编程运算。这对于对编程语言不太熟悉的工程技术人员会是一个难题。本文提出了一种基于Excel和Pro/E的环面蜗杆造型方法，无需大量的编程，运用Excel进行数据计算，再运用PRO/E对这些数值进行处理，对所得曲线、曲面拟合，就可得到环面蜗杆的实体模型。

1 蜗杆齿面的数字化

如图1所示，在蜗杆副的蜗杆上建立两个坐标系，Sj为蜗杆的静坐标系，S1为与蜗杆固联的动坐标系，在其蜗轮上也建立两个坐标系，S0为蜗轮的静坐标系，S2为蜗轮的动坐标系。

为了描述蜗杆接触线，设坐标系S，S的原点与S2的原点重合，z轴与z2轴重合，相位角为ε。

图1 蜗杆副的坐标设置Fig.1 Coordinate setting of worm pair

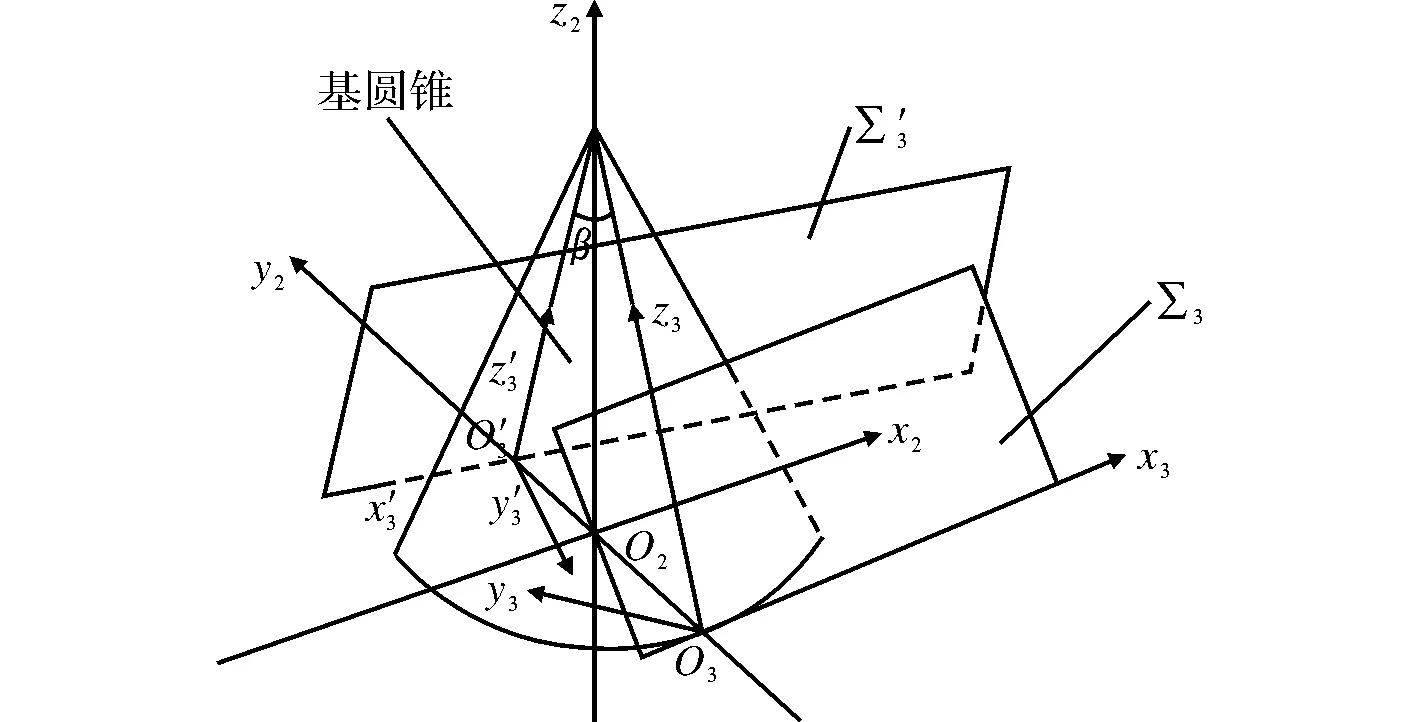
图2 蜗杆的齿面组成Fig.2 Worm gear tooth surface

在坐标系S中，甲面的接触线方程(1)为[6]。

v=u(csoβ/i01+sinβcosφ0)sinφ0-(a-rbsinφ0)sinβsinφ0

x2=uy2=vsinβ-rbz2=vcosβ

x1=-x2cosφ1cosφ0+y2sinφ0cosφ1-z2sinφ1+acosφ1

y1=x2csoφ0sinφ1-y2sinφ0sinφ1-z2sinφ0-asinφ1

z1=-x2sinφ0-y2sinφ0

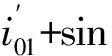
x2=u′cosε-v′sinβsinε+rbsinε

y2=u′sinε-v′sinβcosε+rbcosε

z2=v′cosβ

x1=-x2cosφ1cosφ0+y2sinφ0cosφ1-z2sinφ1+acosφ1

y1=x2cosφ0sinφ1-y2sinφ0sinφ1-z2sinφ0-asinφ1

z1=-x2sinφ0-y2sinφ0

图3 甲乙齿面的关系Fig.3 Party a and b tooth surface

式中，φf≤φ0≤φf+2φaφ1=φ0i01，φf、φa为蜗杆工作起始角和蜗杆包围蜗轮的工作半角；i01为传动比；u的取值范围为

其中，ra0为蜗轮齿顶圆半径；rf0为蜗轮齿根圆半径。

ε=2α+2ξd2180π

式中，α为压力角；ξ为蜗杆节圆齿厚；d2为蜗杆计算圆直径[7]。

1 Pro/E中蜗杆齿面的建模

蜗杆的齿面可以细化为由无数条啮合时的接触线组成，假如得到这些接触线的空间坐标，就最终可以描述蜗杆的齿面。根据方程(1)(2)的关系，在u、φ0的取值范围内给定一值，即可得v，进而可得到接触线上的点，给u不同的值，就可得到当前φ0接触线上不同的点，又因接触线是直线，可取u的最大值与最小值，计算得到相应的空间坐标，相连即为此时的接触线，而在φ0的取值范围内给其一定的步长再根据u的值可得蜗杆齿面上的一系列接触线，对这些接触线进行拟合，就得到蜗杆的齿面。

如某蜗杆参数中心距a=250，传动比i01=40，母平面倾角β=11°，工作起始角φf=3.984 3°，蜗杆包围蜗轮的工作半角φa=18.225 0°。于是蜗杆的工作角范围为

3.984 3≤φ0≤40.434 3

185.563 5≤u≤203.611 3

根据文献[8] Excel解方程组的方法，将式(1)编辑到Excel表格中，给φ0步长0.05，初值为3.984 3，终值为40.434 3，得到244个值，分别以u=185.563 5、u=203.611 3计算得到两组数据，即可求得244条蜗杆接触线上的空间坐标点，再将此数据在记事本中并分别以*.ibl格式保存，如图4所示。同理可得式(2)即蜗杆乙齿面接触线的空间坐标。

图4 接触线空间坐标点Fig.4 Contact line space coordinates point

为验证利用Excel求解方程组的准确性，以φ0=3.984 3，u=185.563 5，通过Mtalab对方程(1)求解，得X1=-20.635 2，Y1=-110.105 3，Z1=-84.487 6，此解与Excel中所求相同，可以得证运用Excel求解的准确性。

在Pro/E中运用插入、模型基准、点、偏移坐标系基准点工具打开以上求得的四组*.ibl文件，得到如图5所示空间点集合，并通过曲线工具连接相应两点，得到蜗杆的接触线。再利用其边界混合工具拟合接触线得到蜗杆的甲乙齿面，如图6所示。最后合并曲面、实体化、去除材料既得环面蜗杆三维模型，如图7所示。

图5 空间坐标点集合Fig.5 Space coordinate point collection

图6 蜗杆甲、乙齿面Fig.6 Party a and b worm tooth surface

图7 环面蜗杆三维模Fig.7 Three-dimensional model of enveloping worm

3 结束语

基于求平面二次包络环面蜗杆接触线对环面蜗杆造型的难点在于对接触线空间坐标点的求解。本文结合Excel和Pro/E对平面二次包络环面蜗杆的方法，既发挥了Excel无需大量编程即可得到一般方程解的优点，亦利用了Pro/E简洁明了的实体造型功能。使建模直观易懂，为不熟悉计算机编程语言的工程技术人员更快得到其三维模型提供了一种可能。

[1] 张彦钦,张光辉.平面包络环面蜗杆副精确实体模型的建立[J].重庆大学学报,2010,22(7)：12-17.

[2] 付大鹏,魏圣可.基于离心泵半开式叶轮的五轴数控加工技术[J].东北电力大学学报,2013,33(3)：23-26.

[3] 张海波,黎甜,白贺.基于Cimatron E的离心泵蜗壳数控加工技术研究 [J].东北电力大学学报,2013,33(3)：1-4.

[4] 谭昕,周红.基于驾驭式虚拟加工的平面二次包络蜗杆实体造型[J].机械设计,2005,22(7)：57-59.

[5] 肖启明,廖学海,钱丽霞,李万全.平面二包络环面蜗杆参数化精准建模研究[J].工程设计学报,2012,19(4)：298-301.

[6] 王永鑫.平面二次包络环面蜗杆副数控加工的编程与仿真技术研究[D].湖南：湘潭大学,2011.

[7] 董学朱.环面蜗杆传动设计和修形[M].北京：机械工业出版社,2004.55-57.

[8] Joseph C.Musto,William E.Howard,Richard R.Williams.MATALAB&Excel工程计算[M].吴文国,林川,译.北京：清华大学出版社,2010.35-41.

Planar quadratic enveloping torus worm model Based on Excel and Pro/E

FU Da-peng, SUN Wen-jie, WANG Li-qian

(School of Mechanical engineering, Northeast Dianli University, Jilin 132012, China)

This article mainly introduced using Excel to solve the equations, and through Mtalab numerical processing method to validate its accuracy, and then obtain the three-dimensional coordinates of points into Pro/E for 3D models of planar quadratic enveloping torus worm. The method fully applied the Excel of solving equations without a large number of data programming advantages, and the Pro/E of easy to master the surface treatment and the solid modeling. The result was faster and more convenient to the planar quadratic enveloping torus worm modeling.

Excel and Pro/E; enveloping worm; 3D modeling

2014-04-08；

2014-06-16

付大鹏 (1960)，男， 教授 ， 主要从事机械振动与数控技术的研究。

TH132

A

1001-196X(2015)01-0076-04