轨索移梁新工艺力学特性分析与试验研究*

颜东煌，潘 权

(长沙理工大学 土木与建筑学院, 湖南 长沙 410114)

轨索移梁新工艺力学特性分析与试验研究*

颜东煌†，潘 权

(长沙理工大学 土木与建筑学院, 湖南 长沙 410114)

针对轨索移梁新工艺在悬索桥建设中的关键技术问题，将轨索节段离散成两节点直线单元，建立轨索移梁系统空载状态下的整体力学分析模型，推导出主缆、吊索、轨索等各构件受力状态的计算方程并求解．设计制作了矮寨悬索桥轨索移梁体系的整体缩尺模型并将模型试验与理论分析结果进行了比较.本文所提方法的计算结果与模型试验结果吻合良好，表明本文计算分析方法正确有效，能解决轨索移梁工艺整体分析求解问题，并可简化计算分析过程，计算精度和结果能够应用于工程的初态分析和求解，是一种适合于轨索移梁工艺空载状态下找形计算分析方法.

悬索桥；主梁施工；轨索移梁工艺；力学分析；模型试验

为了便于运输，在山区修建大跨度地锚式悬索桥时常采用钢桁梁的主梁形式，例如,中国修建的四渡河大桥、坝陵河大桥和矮寨大桥等.主梁施工是山区大跨径悬索桥施工的难点，国内外可行并适应于山区大跨度悬索桥主梁施工的方法主要有缆索吊机施工法、桥面吊机施工法[1]和轨索移梁施工法[2]等，各种施工方法均有成功的案例，但从适用跨径、施工工期、永久用钢量和辅助施工设施等存在较大差异.轨索移梁施工方法通过整体模型试验[3]和足尺模型试验[4]验证了方案可行，并首次在矮寨大桥主梁架设中成功使用，1 000.5 m长的钢桁梁安装只用了2.5个月[2]，大大节省了工期，减少了钢桁梁永久用钢量，体现了新工艺旺盛的生命力，但该工艺尚处于首次实桥使用阶段，要大量推广还需要积累更多的经验，同时对该工艺的认识和研究仍有待进一步加深，例如移梁体系分析过程能否进一步简化，工艺流程能否进一步优化，设备和操作能否标准化等等，这些都制约着该方法能否全面推广和应用.

由主缆、吊索、吊鞍、轨索等组成的移梁系统为双层柔性悬索体系，索系一旦受力，体系将发生比较明显的变形，通过这种变形将使荷载在索结构系统中按刚度分配[4].对于长而柔的吊索结构，在轨索张拉和移梁荷载作用下会伸长和偏位，其变化量不容忽视，在体系变形协调关系中须考虑这个影响，同时轨索张拉过程中吊索力是未知的，需要从体系变形协调关系中隐性求解等等，这就给静力分析和求解带来了难度和复杂性.在该工艺研发过程中，将主缆和轨索均当成分段悬链线用有限元方法求解，计算过程较繁杂，且轨索有较大预张拉力，与两端只考虑自重作用下和吊索力的悬索节段受力有一定的差异.为了简化轨索移梁工艺空载找形分析过程，根据柔索力学分析的基本假定，本文用解析方法，在吊索力未知的情况下，考虑吊索的弹性伸长，建立主缆、吊索、轨索的整体力学模型并编程求解．计算结果与有限元计算结果、模型试验结果对比分析表明，本文分析方法是正确的，可以用到类似结构的工程计算分析中.

1 轨索移梁工艺力学特性分析

1.1 轨索移梁工艺简介

以主缆及永久吊索作为支撑，在吊索下方设置具有水平预张力的移梁索道，索道通过吊鞍与吊索相连，分别在两岸组拼钢桁梁节段，通过运梁小车将单个节段在运梁索道上纵向运输就位至永久吊索下方,用跨缆吊机或其他起吊设备提升钢桁梁节段，退出运梁小车，节段对接并销接吊索，逐节段由跨中向两岸对称施工，直至全桥贯通[2].该工艺实现了加劲梁节段的整段运输，可大幅度减少主梁节段空中作业工作，节省施工工期，降低施工成本，提高施工质量和安全，为山区特大跨度悬索桥主梁施工提供了一套先进、经济、高效的施工工艺，解决了山区特大跨度悬索桥加劲梁施工困难的难题，是山区大跨度悬索桥施工领域的一重大新方法，且施工的机具为常规设备，易于操作和控制,而且该方法也适合于中、下承式拱桥主梁施工，具有较大的适应能力和推广价值.

1.2 轨索移梁空载状态力学分析模型

常规悬索桥施工过程计算时，主缆常采用分段悬链线方法求解，从成桥状态倒拆到空缆状态时，吊索力是明确的，通过迭代可以直接求解空缆的内力和线形、无应力索长、吊索长度等[5-7].常规双层索系、索穹结构计算分析中，常将吊杆刚性处理[8]，或假定吊索刚度无穷大，保证承重索和稳定索的竖向位移相同，这与实际情况存在有一定的偏差.在单层柔性索系有限元分析中，常采用两节点直线单元[9]、两节点曲线单元[10-12]、多节点等参单元[13-14]等来分析求解，虽然各种单元计算精度、计算效率、适应范围等存在有一定的局限性和偏差，但在各自适应范围内的计算结果均能达到较高的计算精度，能够被工程应用[15].

为了简化轨索移梁工艺计算分析过程，根据柔索力学分析的基本假定，本文用解析方法，在吊索力未知的情况下，考虑吊索的弹性伸长，建立主缆、吊索、轨索的整体力学模型并求解，其中主缆节段采用分段悬链线模拟，轨索节段单元采用两节点直线杆单元来模拟，将计算结果与有限元计算结果、模型试验结果进行对比分析.

定义空载状态为主缆、吊索架设完成，吊鞍座和轨索安装就位，轨索张拉完成的状态.为了简化空载状态下体系的计算方法，特做如下假定[5-7]：

1)柔索只能受拉，不能受压和受弯.2)柔索的应力-应变符合胡克定理.3)受力前后主缆、轨索、吊索的抗拉刚度计算时均使用变形前的截面面积.4) 忽略轨索与吊鞍座间的摩擦，吊索在轨索张拉完成后不发生倾斜.

建立如图1所示的移梁体系空载状态下的力学分析模型、模型中字母z代表主缆，字母g代表轨索，字母d代表吊索.为了描述分析过程，抽取如图2所示的一个节间模型进行分析.

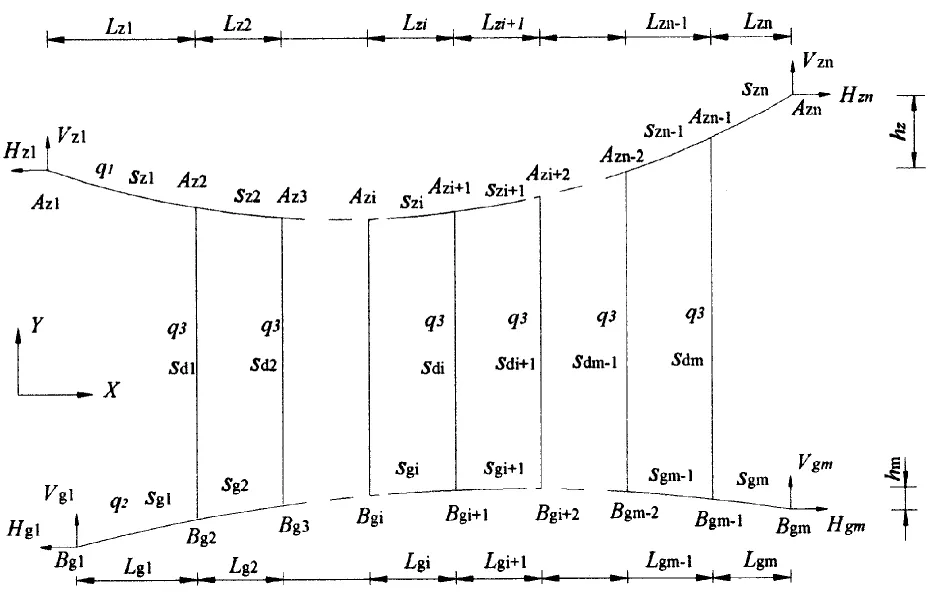
图1 轨索移梁空载体系力学分析模型

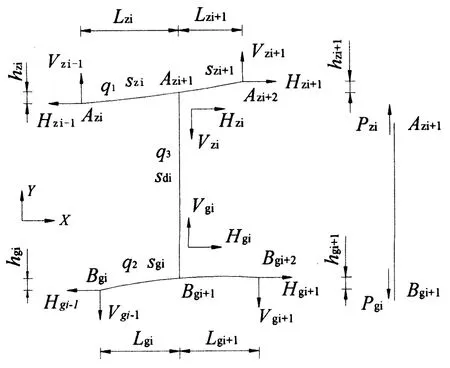
图2 轨索移梁空载体系力学离散模型

1.2.1 主缆受力分析

图2为轨索移梁空载体系力学离散模型.由图2可知，在空载状态下，将主缆节段离散成2个节段Azi-Azi+1，Azi+1-Azi+2，分别建立分段悬链线单元方程[5-7]，并求解得lzi，hzi，lzi+1，hzi+1：

(1)

(2)

lzi+1=Xzi+1-Xzi;

(3)

hzi+1=Yzi+1-Yzi.

(4)

式中：E1，A1分别为主缆弹性模量和截面面积；q1为主缆单位长度的自质量；Szi为空缆安装吊索后的节段索长；i=1～n；其他参数见图1.

根据Azi节点及吊索受力平衡状态，可以建立另外2个方程.

Hzi-1=Hzi;

(5)

Vzi=Vzi-1-Pzi-q1Szi.

(6)

式中：Pzi为Azi节点处吊索作用力.

1.2.2 轨索受力分析

根据轨索应力水平、支撑条件、安全系数及移梁爬坡角等可以确定轨索直径、强度等级和类型等.由于轨索支撑在与吊索下锚点相连的吊鞍上，在空载状态下的线形垂度不大，且由于轨索预张拉力较大，轨索自质量对索段线形的影响有限，且便于后续移梁过程的受力分析，假定轨索张拉完成后各节段为直线，则轨索可离散成多根直线链杆的连接，用两节点直线杆单元来模拟轨索节段空载状态下的受力，得到如图3所示的分析简图．根据静力平衡方程，可以直接得出直线索段的内力和几何方程如式(7)～式(15)所示.

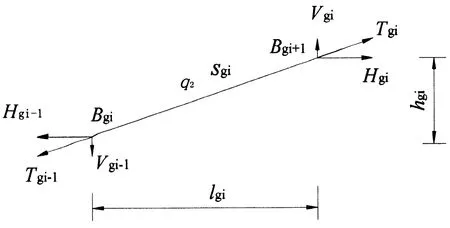
图3 轨索两节点直线杆单元离散图

lgi=Hgi-1Sgi/Tgi-1；

(7)

hgi=Vgi-1Sgi/Tgi-1;

(8)

Δ(Sgi)=TgiSgi/E2A2;

(9)

(10)

Hgi-1=Hgi;

(11)

(12)

Vgi=Vgi-1-Pgi+q2Sgi;

(13)

lgi+1=Xgi+1-Xgi;

(14)

hgi+1=Ygi+1-Ygi.

(15)

式中：E2，A2分别为轨索弹性模量和截面面积；q2为轨索单位长度的自质量；Sgi为轨索节段索长；Pgi为吊索索力增量；i=1～m；其他参数意义见图3.

1.2.3 吊索受力分析

吊索受力相对简单，根据假设4，在空载状态下不考虑吊索的倾斜，实际施工时可以通过预偏或张拉完轨索后二次调整来实现吊索保持垂直状态.吊索受力和变形协调关系为：

Pzi=Pgi+q3Sdi+W;

(16)

Yzi-Ygi=Pgi/E3A3+Sdi.

(17)

式中:W为吊鞍的恒重；E3，A3分别为吊索弹性模量和截面面积；q3为吊索单位长度的自质量；Sdi为吊索无应力索长；其他参数见图1.

1.3 体系求解分析

轨索张拉前，两锚固点的纵向位置lg，预张拉力Tg0，吊索无应力索长Sd i已知，吊索安装完后主缆的索力、线形、索塔间距lz及高差hz可以根据实际计算得出，在此基础上用迭代方法求解其他未知数.其迭代格式如下：

1)假定轨索左支座处的水平力Hg0和标高hg0，主缆左支座处水平力Hz0，吊索索力增量Pg1.

2)由式(5)和式(11)可求得Hzi，Hgi.

3)将2)步的计算结果代入式(10)，式(13)，式(7)，式(8)和式(10)分别得到Vg0，Vg1，lg1，hg1和Tg1.

4)由变形协调关系，结合式(15)，式(17)，式(4)分别得到Yg1，Yz1，hz1.

5)将hz1计算结果代入式(2)，式(1)可以求得Vz0，lz1.

6)将5)步计算结果代入式(6)，式(16)和式(13)分别得到Vz1，Pz1,Vg2．

7)将6)步计算结果代入式(2)，式(1)，式(10)，式(7)，式(8)后分别求得hz2，lz2，Tg2，lg2，hg2.

8)将7)步计算结果代入式(4)，式(15)，式(17)求得Yz2，Yg2，Pg2.

9)按此迭代求得所有的lgi，lzi，hgi，hzi.

至此可以求得所有的吊索力和各节点的坐标，代入式(9)，式(12)等可以求得轨索的无应力索长、轨索锚固点标高等.

2 轨索移梁整体模型试验

矮寨悬索桥主梁节段首次在轨索上滑移实现水平方向移动，水平索道采用8根相对独立的60-ZZZ-1570型密封钢丝绳作为轨索，茶洞岸一侧轨索采用OVM-CPS剪力分散型岩锚体系锚固，吉首岸一侧轨索采用平衡配重的形式锚固，并保证单根轨索预张拉力为105t[2].按照1∶33的几何缩尺比设计和制作整体试验室内模型，缩尺后模型主缆孔跨尺寸为7.333m+35.636m+3.515m，主缆中心间距为818mm,吊索的纵向间距为439.4mm.见图4.

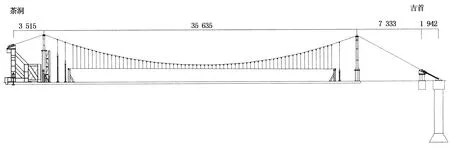
图4 矮寨悬索桥整体模型示意图(单位：mm)

试验模型由2个锚碇系统、2根主缆、68对吊索及索夹、3对岩锚索、2个索塔及索塔支墩，轨索及轨索张拉装置、测试系统等组成，具体设计见文献[3].根据应力一致，轴向刚度相似原则设计轨索各参数，选用4根φ2.5mm高强度镀锌钢丝绳等代轨索，并设计如图5所示的轨索张拉装置，通过调整螺杆和螺母的相对移动实现轨索张拉，压力传感器可实时监测轨索索力的变化.

图5 轨索张拉锚固、索力测试装置

根据整体模型试验设计，采用有限元软件MIDASCivil建模，建立全桥空缆初态数值模型.试验

过程中通过调整试验模型空缆状态，保证空缆状态与有限元分析模型一致.安装完成索夹、吊索、吊鞍，3对岩锚索张拉到位，张拉4根轨索，并保证吊索处于垂直工作状态，测试张拉工况下主缆力和线形、岩锚索索力、轨索线形、吊索索力等的变化情况.

3 测试结果分析

轨索张拉完成后，将有限元计算结果、模型试验测试结果、本文计算结果进行比较，限于篇幅，只抽取几个典型位置的响应进行了对比，见表1．主缆锚固点的索力结果见表2.

表1 轨索张拉工况对体系线形的影响分析表

注：实测值为上下游测点的平均值，X向测点向吉首岸侧移动为负，Y向测点向上为负，反之为正.

表2 轨索张拉工况对主缆力的影响分析表

由表1可知，本文分析方法与实测值、有限元值在Y向的偏差较小，最大偏差分别为4.36%和4.00%.由表2可知，锚固点主缆力偏差不大，最大为2.34%，中跨跨中、吉首岸侧1/4跨、茶洞岸侧1/4跨主缆变位X向偏差相对较大，主要由于X向总体变形值较小，测试系统的精度等引起的偏差较大.试验结果和计算结果对比分析表明,本文分析方法能应用到轨索移梁体系空载状态下的找形计算分析中，从而可以简化轨索移梁体系分析过程，简化后的计算结果与有限元计算结果、模型试验结果偏差基本小于5%，能被工程计算所接受.

4 结 论

1)通过理论推导建立了轨索移梁系统空载状态下的主缆、吊索和轨索的整体力学分析模型，由结构变形后的位置建立的平衡方程，能进行结构大变形的几何非线性分析，在轨索移梁工艺计算分析中，简化的计算分析过程可以达到足够的精度，能够被工程所应用.

2)在轨索移梁体系的初始几何状态未知的情况下，可以通过假定轨索的初始力或位形进行迭代计算得到轨索的真实内力和几何形状.

3)设计的轨索张拉和测试装置能基本满足试验要求，模型试验主缆线形、主缆力实测结果与理论计算结果吻合良好.

[1] 刘高,彭运动,周平,等. 坝陵河大桥钢桁加劲梁施工架设方案研究[J].公路交通科技，2009,26(5)：80-85.

LIU Gao , PENG Yun-dong , ZHOU Ping,etal. Research on erection methods of steel stiffening truss girder for baling river bridge[J]. Highway and Transportation Research and Development, 2009,26(5):80-85.(In Chinese)

[2] 易继武，盛希，张念来,等. 矮寨特大悬索桥钢桁加劲梁架设方案研究[J].施工技术, 2013，42 (5): 9-11.

YI Ji-wu，SHENG Xi，ZHANG Nian-lai,etal. Study on the erection of steel stiffening truss girder for aizhai bridge[J].Construction Technology, 2013,42 (5):9-11.(In Chinese)

[3] 冯剑.矮寨特大悬索桥缩尺模型设计研究[D].长沙:长沙理工大学土木与建筑学院，2010：23-45.

FENG Jian .The research on scale model design of aizhai suspension bridge[D].Changsha: School of Civil Engineering and Architecture，Changsha University of Science and Technology,2010：23-45.(In Chinese)

[4] 沈锐利，闫勇，唐茂林,等. 轨索滑移法节段足尺模型试验设计与安装[J].桥梁建设，2013，43(1)：15-22.

SHEN Rui-li,YAN Yong , TANG Mao-lin,etal. Design and installation of full-scale sectional model for testing of rail cable launching method[J].Bridge Construction, 2013,43(1): 15-22.(In Chinese)

[5] 张莉, 张其林,丁佩民.悬索结构初始状态及放样状态的确定分析[J] .同济大学学报:自然科学版，2000，28(1):9-13.

ZHANG Li, ZHANG Qi-lin, DING Pei-min.Initial equilibrium and geometry zero state solution methods for cable structures [J]. Journal of Tongji University：Natural Science,2000,28(1):9-13.(In Chinese)

[6] 唐茂林.大跨度悬索桥空间几何非线性分析与软件开发[D].成都：西南交通大学土木工程学院，2003：57-63.

TANG Mao-lin. 3D geometric nonlinear analysis of long-span suspension bridge and its software development[D]. Chengdu: College of Civil Engineering,Southwest Jiaotong University,2003：57-63.(In Chinese)

[7] 潘永仁，范立础. 大跨度悬索桥加劲梁架设过程的倒拆分析方法[J].同济大学学报:自然科学版，2001，29 (5) :510-514.

PAN Yong-ren, FAN Li-chu. Backward analysis method of long span suspension bridges for erection of stiffening girders[J].Journal of Tongji University：Natural Science, 2001,29(5):510-514.(In Chinese)

[8] 张文福,孙晓刚,张红星,等. 预应力双层索静力分析的能量变分解[J].空间结构，2007,13(1)：29-31.

ZHANG Wen-fu,SUN Xiao-gang,ZHANG Hong-xing,etal.Energy variational solutions for static analysis of pre-stressed double layer suspended cable structures[J]. Spatial Structures,2007,13(1)：29-31.(In Chinese)

[9] 唐建民,赵引,吴黎华. 基于欧拉描述的两节点索单元非线性有限元法[J].上海力学,1999,20(1)：89-94.

TANG Jian-min, ZHAO Yin ,WU Li-hua. A eulerian geometrically non-linear finite element method with two-node cable element for the ananlysis of cable structures[J].Shanghai Mechanics , 1999,20(1):89-94.(In Chinese)

[10]杨孟刚,陈政清. 基于UL列式的两节点悬链线索元非线性有限元分析[J].土木工程学报,2003,36(8):63-68.

YANG Meng-gang, CHEN Zhen-qing.The non-linear finite element analysis for two-node catenary element of cable structure based on UL formulation[J].China Civil Engineering,2003,36(8)：63-68.(In Chinese)

[11]胡建华，王连华，赵跃宇.索结构几何非线性分析的悬链线索单元法[J].湖南大学学报:自然科学版，2007,37(11):29-32.

HU Jian-hua,WANG Lian-hua, ZHAO Yue-yu.A catenary cable element for the nonlinear analysis of cable structures[J]. Journal of Hunan University:Natural Sciences, 2007,37(11):29-32.(In Chinese)

[12]袁行飞, 董石麟. 二节点曲线索单元非线性分析[J] . 工程力学, 1999, 16( 4) : 59- 64.

YUAN Xing-fei, DONG Shi-lin. A two-node curved cable element for nonlinear analysis[J].Engineering Mechanics, 1999, 16( 4) : 59- 64.(In Chinese)

[13]唐建民,沈祖炎,钱若军.索弯顶结构非线性分析的曲线索单元有限元法[J].同济大学学报:自然科学版，1996,24(1):6-10.

TANG Jian-min,SHEN Zu-yan,QIAN Ruo-jun. Finite element method with curved cable element for the nonlinear analysis of cable domes[J]. Journal of Tongji University:Natural Science,1996,24(1):6-10.(In Chinese)

[14]程大业.悬索结构分析的精确单元方法[D].北京：清华大学土木水利学院，2005：25-30.

CHENG Da-ye. Exact element method for analysis of cable structures[D]. Beijing:Civil Engineering and Water Resources Institute，Tsinghua University，2005：25-30.(In Chinese)

[15]沈锐利,张丁盛,沈子钧. 空中客车交通系统悬索结构的力学特性[J].土木工程学报，2004，37(4)：13-18.

SHEN Rui-li , ZHANG Ding-sheng, SHEN Zi-jun .The mechanical properties of the suspension cable structure in aerobus transit system[J]. China Civil Engineering ,2004,37(4)：13-18.(In Chinese)

[16]包立新.高空悬挂运输系统的静-动力研究[D].成都：西南交通大学土木工程学院，2007：21-46.

BAO Li-xin . Analysis of aerobus transportation system static & dynamic behavior[D].Chengdu:College of Civil Engineering，Southwest Jiaotong University，2007：21-46.(In Chinese)

Force Analysis and Model Test for New Rail Cable Launching Method under Non-loading Condition

YAN Dong-huang†, PAN Quan

(School of Civil Engineering and Architecture, Changsha Univ of Science and Technology, Changsha, Hunan 410114, China)

The integral mechanic model of the non-loading rail cable launching system was established to deal with the stiffening girders construction in suspension bridge. The rail cable segment was discretized into two-node line element. And the governing equations for the rail cable launching system, which consists of the main cable, the sling, the saddle and the rail cable, were determined. Moreover, a 1∶33 reduced-scale experimental model for the rail cable launching system of Aizhai suspension bridge was constructed. The conclusions obtained from the theoretical analysis and experiments were compared. It is shown that the results of presented calculation method match well with that from the model test. Also, the accuracy and effectiveness of the proposed method are manifested, which can be used to solve the problem about rail cable launching system and simplify the calculating process. The calculation accuracy and results for this method can be employed to the initial-state analysis. This indicates that the recommended analytical method is suitable for shape-looking calculation and analysis of the non-loading rail cable launching technology.

suspension bridges;stiffening girder construction;rail cable launching method;mechanical analysis;model test

1674-2974(2015)05-0080-06

2014-12-23

国家自然科学基金资助项目(51178058), National Natural Science Foundation of China(51178058)；湖南省科技计划资助项目(2012FG4256)；长沙理工大学桥梁与隧道工程创新性项目(11ZDXK01)

颜东煌(1961-)，男，湖南娄底人，长沙理工大学教授，博士生导师

†通讯联系人，E-mail: yandonghuang@126.com

U448.25

A