大型风电机组组合式塔架结构优化设计*

陈俊岭，阳荣昌，马人乐

(同济大学 建筑工程系,上海 200092)

大型风电机组组合式塔架结构优化设计*

陈俊岭†，阳荣昌，马人乐

(同济大学 建筑工程系,上海 200092)

为解决传统单管风力发电塔架在大型风电机组应用中加工、制作、安装和运输成本大幅上升的问题，提出一种新型组合式塔架结构，并对其进行结构优化设计.该塔架上部为传统单管式塔架,下部为四角钢十字形组合截面塔柱的格构式塔架.通过对四角钢十字形组合截面的轴压极限承载力进行分析，得到组合截面的稳定系数曲线.基于粒子群算法，综合考虑应力、频率和长细比约束等因素，对下部格构式塔架的形状和杆件截面进行优化.分析结果表明，组合式塔架结构可以解决传统单管式风力发电塔架的运输问题，且用钢量节省约34%.

风力发电塔；格构式塔架；结构优化；粒子群算法；四角钢十字形组合截面

随着传统化石能源的不断消耗，能源问题已经成为世界各国共同面对的一个巨大挑战，发展风电技术成为解决能源问题的有效途径之一.增加轮毂高度可获得更大的电力生产能力，这要求更高的支撑塔架把机舱和叶片等部件举到设计高度.单管塔结构形式简单、占地面积小、外形美观，因此在风力发电塔中应用非常普遍.但随着塔架高度的增加，钢管的直径越来越大，导致钢板厚度越来越大、加工困难、经济性变差[1].当轮毂高度超过100 m后，钢管直径还可能超过公路运输限高，使得运输困难.因此，研究人员开始寻求可替代的结构形式，格构式塔架开始进入人们的视野.郑瑞杰和马人乐[2]提出一种新型变截面构架式风力发电塔架并以某3 MW风机为例进行优化设计，指出构架式塔架相比单管式塔架具有刚度大和运输方便等优点.Dehm[3]介绍了德国某2.5 MW风电机组160 m高全格构式角钢塔架的设计和施工，指出格构式塔架可用于建造更高的风力发电塔架.Seidel[4]介绍了某5 MW风电机组的支撑结构设计，其上部为单管塔，下部格构式钢管塔架的塔柱和斜杆之间通过铸钢节点连接.本文结合格构式角钢塔架和单管塔架的优点，提出一种下部为格构式角钢塔架、上部单根钢管组合而成的新型风力发电塔架结构形式，并以某轮毂高度110 m的1.5 MW风力机为原型，采用粒子群优化算法，考虑结构频率等约束条件对组合塔架进行了优化设计.

1 组合式塔架

对于一般的电视塔、输电塔等高耸结构，虽然风荷载在结构设计中起控制作用，但由于风荷载的频遇值较低，一般不会引起结构疲劳破坏.风电机组塔架则不同，不仅要承受很强的风荷载，还要承受风轮旋转产生的周期性作用力，疲劳荷载往往成为影响结构设计的重要因素.由于应力集中、焊接缺陷、残余应力等因素的影响，焊接结构的疲劳强度远低于钢材的强度设计值，因此风电机组格构式塔架的构件之间应尽量避免焊接.常见的格构式塔架构件一般为角钢或钢管，角钢构件制作简单，工厂简单切割和钻孔后现场螺栓连接即可；钢管构件或钢管与角钢之间采用法兰、单剪或双剪连接，但不管采用哪种连接方式，钢管上均需焊接连接件.为充分利用材料的疲劳强度，提高塔架结构的抗疲劳性能，新型风力发电组合式塔架(图1(a))，单管式塔架(图1(b))除局部节点采用对接焊外，主要构件之间均采用摩擦型高强螺栓连接.

图1 组合式和单管风力发电塔

由于风电机组顶部机舱、叶片等部件的重量和迎风面积较大，导致塔柱内力比一般高耸结构大很多.为此，下部格构式塔架的塔柱采用四角钢十字形组合截面(图2(a))，横杆、斜杆和横膈等杆件采用单角钢或双角钢T形截面(图2(b))，通过间隔设置的填板和螺栓保证组合截面的协同受力.塔架斜杆与水平轴夹角为45°左右.为防止塔身和叶片碰撞，叶片范围内塔架为单根钢管.主要构件(包括角钢和钢管)材料均为Q345B，高强螺栓为10.9级.

格构式塔架顶部的宽度B1根据上部单管塔底部的直径D、变坡角β和转换节点高度h确定.

(1)

轮毂高度和风轮直径确定后，格构式塔架高度H便相应确定.当保持斜杆与水平轴的夹角不变时，格构式塔架各段宽度为等比数列.若给定塔架底部宽度B0，便可利用递推关系由H,B0和B13个参数确定格构式塔架的几何形状.

图2 组合截面

2 四角钢十字形组合构件极限承载力

根据GB 50017-2003《钢结构设计规范》[5]第5.1.2条规定，四角钢十字形组合截面作为轴心受力构件时，稳定系数按b类截面计算，构件的长细比不得小于5.07b/t.风电机组的机舱和叶片安装在塔架顶部，使得塔顶作用有较大的重力荷载和风荷载，因此四角钢十字形组合截面塔柱的内力较大，角钢需要采用L180×14,L180×16,L180×18等规格, 板件的宽厚比b/t为10～12.85，因此构件的长细比小于50.7～65时不能按规范公式进行稳定承载力验算.本文为后续组合式塔架优化分析的开展，采用通用有限元分析软件ANSYS对四角钢十字形组合截面的轴压承载力进行了深入研究.

2.1 有限元模型

杆件的计算简图如图3所示，其中v0为杆件初弯曲(扭转屈曲时为初始缺陷幅值)，取杆件长度的1/1 000[6]，基于一致模态缺陷法引入初始几何缺陷.角钢和填板用Shell181单元模拟，采用接触单元Conta173和Targe170模拟角钢之间组合作用，通过结点耦合模拟填板和角钢之间的螺栓连接.角钢的残余应力分布形式与文献[5]中柱子曲线残余应力分布形式一致，即按对称分布模式考虑(图4(a))，其中正号代表受拉，负号代表受压，fy为钢材的屈服强度，取为345 MPa.β可在区间[0.15,0.3]内取值，本文取0.2.钢材本构采用理想弹塑性模型，如图4(b)所示，弹性模量E取2.06×105MPa，泊松比取0.3.

图3 计算简图

2.2 模型验证

国内外很多学者对双角钢十字形组合截面柱的承载力进行了试验和理论研究[7-10].为验证本文有限元模型的正确性，选取刘红军和李正良[9]单节间偏心受压试验中L14-2-a和L14-2-b两根试件进行模拟，角钢截面为L160×14，试件长度为1 860mm，长细比为30.L14-2-a试件的压力差为20%，L14-2-b试件的压力差为30%(文献[9]通过压力差确定偏心距).角钢的屈服强度根据给定的材性试验结果确定，有限元模型的边界条件、荷载条件、材料本构模型及其他相关参数和文献[9]一致，有限元模型如图5所示.

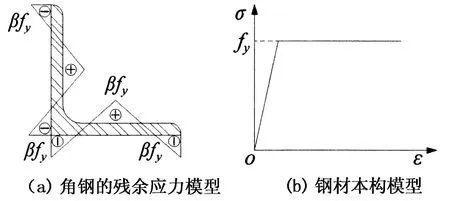
图4 角钢残余应力分布和钢材本构模型

图5 文献[9]试件有限元模型

图6为试件L14-2-b在极限荷载下的应力分布和变形图.从图中可以看出，角钢的破坏模式以弯曲失稳为主.提取C点沿杆轴方向应变随荷载变化的曲线，并与文献[9]给出的试验数据进行对比，如图7所示.从图7可以看出，本文计算结果和文献[9]试验结果吻合较好，最大值略小于试验值，试件L14-2-a和L14-2-b的误差分别为-6%和-1%，验证了双角钢组合截面有限元模型的正确性.

图6 试件L14-2-b应力和变形(单位：MPa)

图7 试件荷载-应变曲线

2.3 十字形组合截面稳定系数

取四角钢十字形组合截面构件的长细比λx范围为[20,150]，选取型号L180×14,L180×16,L180×18,L200×14,L200×16,L200×18,L200×20和L200×24的等边角钢为分析对象.当角钢肢背间距δ(即填板厚度)为2t/3～1.5t(t为角钢厚度)时，对组合截面的回转半径影响不大，分析时取δ=t.根据GB 50017-2003[5]第5.1.5条规定，填板间距取为40i，i为截面回转半径.基于2.1节方法建立四角钢十字形组合截面有限元模型如图8所示.

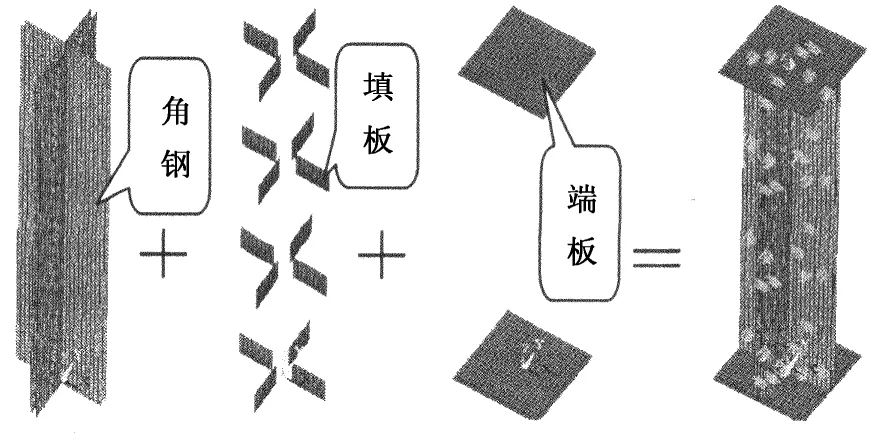
图8 四角钢组合十字形截面柱有限元模型(L200×14，λ=30)

对不同长细比构件进行线性屈曲分析，发现四角钢十字形组合截面构件的屈曲模态和杆件长细比及板件宽厚比有关.当杆件长细比较小时，构件一阶屈曲模态为扭转屈曲；当杆件长细比较大时，构件一阶屈曲模态为弯曲屈曲.扭转屈曲和弯曲屈曲的临界长细比与板件宽厚比近似成线性关系，拟合公式为：

λcr=5.129b/t-6.280.

(2)

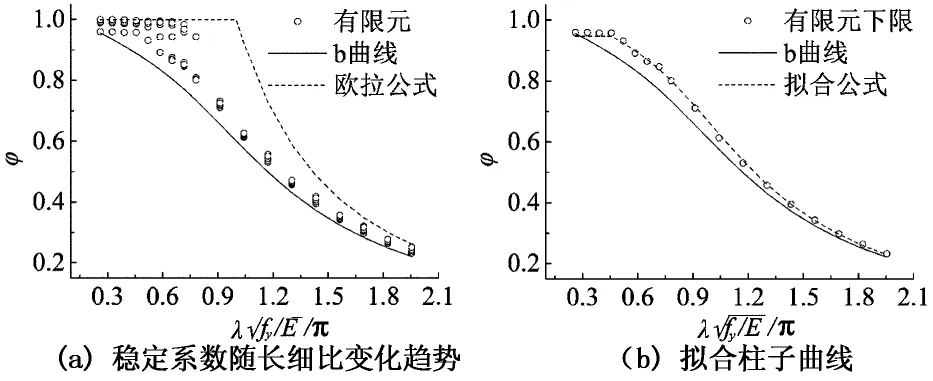
图9 四角钢十字形组合截面柱稳定系数

选取有限元计算结果的下限值拟合四角钢组合十字形截面的柱子曲线，拟合时采用分段函数的方式，并保持曲线的连续性.当0.261≤λn<0.456时，φ取为常数；当λn≥0.456时，选用GB50017-2003[5]所采用的Perry公式形式的表达式(3)，求得α2=0.931,α3=0.250，拟合曲线见图9(b).

(3)

3 组合式塔架设计优化

一般而言，风力发电机组中的塔架结构造价约占总造价的20%左右，且随着功率的增加进一步加大.因此，采用优化算法对结构进行优化设计对进一步降低结构造价有重要意义.Gencturk等[11]基于禁忌搜索算法对某100 kW小型风力发电机组角钢塔架的杆件尺寸进行了优化.Zwick等[12]以风电机组塔架生命周期为目标函数，采用迭代优化方法对某100 m高的格构式钢管塔架的杆件厚度进行了优化，并对关键参数进行了敏感性分析.郑瑞杰和马人乐[2]采用遗传算法(GA)对所提出的构架式风力发电塔架进行了截面尺寸优化和形状优化，表明构架式风力发电塔架比传统单管塔可降低17%的成本.粒子群算法(Particle Swarm Optimization，简称PSO)是由Kennedy和 Eberhart[13]基于对鸟群觅食行为的研究而提出的一种新的进化算法，因其具有高效、鲁棒性好和容易编程实现且可以处理非线性问题的特点而广泛应用于工程优化设计[14].本文采用粒子群算法对新型塔架下部的格构式塔架的形状和杆件截面进行优化.

3.1 粒子群算法

PSO在数学上可描述为：若种群中有n个粒子，表示成X=(X1X2…Xn)，每个粒子为d维向量Xi=(xi1xi2…xid)T，其中的元素xij(i=1, 2, …,n;j=1, 2, …,d)对应于每个需要优化的变量.每个粒子对应的速度记为Vi=(vi1vi2…vid)T，个体最优位置记为Pbesti=(Pbesti1Pbesti2…Pbestid)T；群体的最优位置记为Gbesti=(Gbesti1Gbesti2…Gbestid)T.每个粒子中第k个元素更新速度和位置的规则分别为：

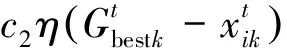
(4)

(5)

式中：t为当前迭代步，则(t+1)为下一迭代步；w为惯性权重，取值为0.1～0.9，本文采用线性递减的惯性权重；c1和c2为加速度因子，根据文献[14]分析结果取c1=3，c2=1；ξ和η为0～1的随机数；r为约束因子，取值为1.

3.2 待优化变量

如前所述，B0为影响塔架形状的关键参数，将其确定为待优化变量之一.其余待优化变量为各杆件的截面尺寸，对于等边角钢主要包括角钢肢宽和角钢壁厚，对于不等边角钢还需区分长肢宽和短肢宽.常用型钢表中不等边角钢长肢和短肢的比值平均为1.58，在优化分析时不等边角钢只设置长肢宽为变量，短肢宽根据该比值求得.次斜杆角钢厚度均取10mm.为尽量减少截面种类和优化变量数目，将各节段的各类型杆件分组，同一组内的杆件几何尺寸参数取值相同，同时根据长细比限值预估截面尺寸的取值范围.

3.3 优化模型

3.3.1 有限元模型

采用有限单元法计算杆件内力和塔架结构动力特性.根据格构式塔架中杆件和单管塔的受力特点，分别采用空间杆单元和空间梁单元模拟，单管塔和格构式塔架之间通过8个一端铰接一端刚接的梁单元连接，以模拟转换节点的作用，单元的特性矩阵具体参考文献[15].该平面内的杆件需要在节点模型中加以校核，整体优化分析时不予考虑.叶片、轮毂和机舱凝聚成集中质量置于塔顶[16]，根据反迭代法[15]求解结构的一阶频率.

3.3.2 约束条件

结构杆件截面优化设计通常指在给定区间内改变杆件截面或塔架外形几何尺寸，使得结构重量最小，同时满足强度、变形、稳定等指标.对于文中的塔架结构，目标函数为下部格构式塔架的重量最小，约束条件为应力约束、长细比约束、变形约束、加速度约束和频率约束，其中变形约束和加速度约束主要是保证机组的正常运行.本文风轮转速为9.7 ～19.5r/min，取塔架一阶固有频率介于1P上限和3P下限的中间值0.4Hz以避免共振.塔架顶部变形和加速度需要通过动力分析获取，且对零部件设计不起控制作用，因此优化分析时不予考虑，可放在后续动力分析中校核.塔架优化的数学描述为：

minimizeW=∑ρiLiAi，

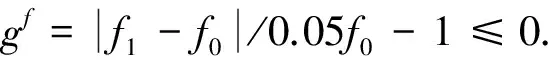
(6)

式中：ρ为钢材密度；L为杆件长度；A为杆件横截面面积；σ为杆件的计算应力，[σ]为允许应力；λ为杆件的计算长细比，[λ]为允许长细比；f1为整体塔架一阶频率，f0为目标频率，根据前文分析取0.4 Hz.通过构造罚函数的方式将有约束问题转化为无约束问题，考虑约束条件的目标函数可表示为：

(7)

式中：p为罚因子，可根据具体问题设置为一个较大的数，本文取10.

3.3.3 荷载条件

考虑风轮传递给塔架的荷载，塔身风荷载和塔架自重.上部单管塔传递给下部格构式塔架的荷载来源于荷载报告，其中极限荷载工况16个，等效疲劳荷载1个.表1给出了部分工况的极限荷载(水平合力最大和合弯矩最大)及等效疲劳荷载.极端风况下，机组处于停机状态，塔身风荷载根据GB 50009-2012《建筑结构荷载规范》[17]计算，风速和风剖面参数根据文献[18]确定.需要注意的是，风荷载计算时需要考虑0°和45°两个风向角.

3.3.4 构件验算

杆件的应力按照GB 50017-2003[5]计算，塔柱稳定系数按式(3)取，杆件应力比控制在0.9以下.需要注意的是，在验算塔架杆件的应力时需要同时考虑极限强度和疲劳强度.极限强度的验算按照GB 50017-2003[5]执行，而疲劳强度的验算按照文献[18]执行.

表1 格构式塔架顶部荷载

3.4 优化结果

经过2 000次迭代后收敛到比较满意的结果，下部格构式塔架重量113 t.图10为格构式塔架总重量的进化曲线(为便于显示，只给出前500次迭代的结果)，各变量的优化结果见表2.由于实际的轧制角钢有规格限制，需要根据实际情况对最终的结果进行调整，调整时按照等面积代换的原则.将调整后的杆件截面代入目标函数中，塔架的总重量为 119 t，塔架的频率为0.382 Hz.优化后，塔架锥角α为85°，斜杆和水平面夹角θ为48.3°，这和通常的设计经验吻合，从侧面反映了结果的合理性.传统单管式塔架重量约为160 t，比组合式塔架重约34%.

迭代次数

表2 优化变量和优化结果

4 结 论

本文提出了一种由下部格构式角钢塔架和上部单管塔组合而成的新型风电机组塔架体系.格构式塔架的塔柱采用四角钢十字形组合截面，除局部节点部位有焊接外，主要构件之间均采用摩擦型高强螺栓进行连接，可充分利用材料的疲劳强度，提高塔架结构的抗疲劳性能，解决了单管塔应用于轮毂高度超过100 m的风电机组时在加工、运输方面的局限性，降低了结构用钢量，具有一定的工程意义.通过对四角钢十字形组合截面的极限承载力分析，发现该类截面的柱子曲线介于GB 50017-2003[5]的b曲线和欧拉公式之间，为后续结构优化分析奠定了基础.基于粒子群优化算法，对下部格构式塔架进行了形状和截面优化，结果表明四角钢组合截面作为格构式塔架的塔柱具有较高的结构效率；格构式塔架锥角为85°、斜杆和水平面的夹角为48°时，其重量较优；对于本文轮毂高度110 m高的1.5 MW风力发电机，采用组合式塔架比单管塔可节省钢材约34%.

[1] HAU E. Wind turbines: fundamentals, technologies, application, economics [M]. 3rd ed. Berlin: Springer, 2013:496-499.

[2] 郑瑞杰,马人乐.变截面构架式风力发电塔架GA 优化[J]. 土木建筑与环境工程, 2007,31 (6): 1-6.

ZHENG Rui-jie, MA Ren-le. GA optimization for variable cross section frame wind turbine[J]. Journal of Civil, Architectural & Environmental Engineering, 2007,31 (6): 1-6. (In Chinese)

[3] DEHM J.160-m-Fachwerkturm für eine windenergieanlage: die höchste windenergieanlage der welt[J]. Stahlbau, 2007,76(4): 213-221.(In German)

[4] SEIDEL M. Jacket substructures for the REpower 5M wind turbine[C]// Conference Proceedings European Offshore Wind. Berlin: EWEA, 2007.

[5] GB 50017-2003 钢结构设计规范[S].北京: 中国计划出版社, 2003: 36-45.

GB 50017-2003 Code for design of steel structures[S]. Beijing: China Planning Press, 2003: 36-45. (In Chinese)

[6] GB 5020-2001 钢结构工程施工质量验收规范[S]. 北京: 中国计划出版社, 2002:31.

GB 5020-2001 Code for acceptance of construction of steel structures[S]. Beijing: China Planning Press, 2002: 31. (In Chinese)

[7] 李振宝, 石鹿言, 刑海军, 等. Q420双角钢十字组合截面压杆承载力试验[J]. 电力建设, 2009,30(9):8-11.

LI Zhen-bao, SHI Lu-yan, XING Hai-jun,etal. Research on bearing capability of Q420 dual-angle steel cross combined section[J]. Electric Power Construction, 2009,30(9):8-11. (In Chinese)

[8] 杨隆宇.特高压输电塔组合截面构件承载力理论与试验研究[D]. 重庆:重庆大学土木工程学院, 2011: 13-31.

YANG Long-yu. Theoretical and experimental investigations on bearing capacity of built-up section member in UHV transmission tower[D]. Chongqing: College of Civil Engineering,Chongqing University, 2011:13-31. (In Chinese)

[9] 刘红军,李正良.双角钢十字组合截面偏心压杆承载力研究[J].四川大学学报:工程科学版, 2012,44(1):63-68.

LIU Hong-jun, LI Zheng-liang.Study on ultimate strength of eccentric compression members with combined angle iron cross-section[J]. Journal of Sichuan University: Engineering Science, 2012,44(1):63-68. (In Chinese)

[10]YAN Zhu-ge, JULIE E M, XING Ma. Modelling of steel lattice tower angle legs reinforced for increased load capacity[J]. Engineering Structures, 2012, 43:160-168.

[11]GENCTURK B,ATTAR A,TORT C. Optimal design of lattice wind turbine towers[C]// 15th World Conference on Earthquake Engineering. Lisbon: IAEE ,2012.

[12]ZWICK D, MUSKULUS M, MOE G. Iterative optimization approach for the design of full-height lattice towers for offshore wind turbines[J]. Energy Procedia, 2012, 24: 297-304.

[13]KENNEDY J, EBERHART R. Particle swarm optimization [C]// IEEE International Conference on Neural Networks. Perth: IEEE Neural Networks Council, 1995: 1942-1948.

[14]PEREZ R E,BEHDINAN K. Particle swarm approach for structural design optimization[J]. Computers and Structures, 2007, 85(19/20): 1579-1588.

[15]王勖成.有限单元法[M].北京: 清华大学出版社, 2003: 329-499.

WANG Xu-cheng. Finite element method[M]. Beijing: Tsinghua University Press, 2003:329-499. (In Chinese)

[16]PROWELL I,VELETZOS M, ELGAMAL A,etal. Experimental and numerical seismic response of a 65 kW wind turbine [J]. Journal of Earthquake Engineering, 2009, 13(8):1172-1190.

[17]GB 50009-2002 建筑结构荷载规范[S].北京: 中国建筑工业出版社, 2012:30-60.

GB 50009-2002 Load code for the design of building structures[S]. Beijing: China Architecture & Building Press, 2012: 30-60. (In Chinese)

[18]GERMANISCHER L. Guideline for the certification of wind turbines [M]. Hamburg: Germanischer Lloyd, 2010: 4-7.

Structural Design Optimization of a Composite Tower for Large Wind Turbine Systems

CHEN Jun-ling†, YANG Rong-chang, MA Ren-le

(Dept of Structural Engineering, Tongji Univ, Shanghai 200092, China)

Traditional tubular wind turbine towers may result in a great increase in the fabricating, mounting and transporting cost for large wind turbine systems. A new composite tower was proposed and then the structural optimization was carried out. The new structure is composed of a lattice tower at the bottom with four-angle combined cross-section legs and the steel tube at the top. The stability coefficients curve of the four-angle combined cross-section column subjected to axial compression was first obtained by a series of ultimate bearing capacity analyses. Considering the strength, frequency and slenderness ratio as constraint conditions, the shape and section optimization of the lower lattice tower was carried out. The optimal results show that the proposed structural system can resolve the scarcity of traditional tubular steel towers in transportation and has a 34% less steel consumption.

wind turbines; lattice tower; structural optimization; particle swarm optimization; four-angle combined cross-section

1674-2974(2015)05-0029-07

2014-08-03

国家自然科学基金资助项目(51378381), National Natural Science Foundation of China(51378381)

陈俊岭(1974-)，女，河北景县人，同济大学副教授，博士

†通讯联系人，E-mail:chenjl@tongji.edu.cn

TK83；TU359

A