基于MCMC算法的贝叶斯面板单位根检验
2015-03-08李素芳朱慧明
李素芳,朱慧明,李 荣
(1. 湖南大学 工商管理学院, 湖南 长沙 410082;2. 中南财经政法大学 统计与数学学院, 湖北 武汉 430073)
基于MCMC算法的贝叶斯面板单位根检验
李素芳1,2†,朱慧明1,李 荣1
(1. 湖南大学 工商管理学院, 湖南 长沙 410082;2. 中南财经政法大学 统计与数学学院, 湖北 武汉 430073)
针对面板单位根检验存在检验势不稳定和原假设设置主观选择的问题,提出基于面板数据分位自回归模型,选择非对称Laplace分布的似然函数对模型进行贝叶斯分位回归分析.结合参数的完全条件分布设计MCMC抽样算法,进行贝叶斯分位单位根检验,并利用Monte Carlo模拟实验研究了贝叶斯分位单位根检验的有效性与可行性.研究结果表明,基于面板数据分位自回归模型的贝叶斯单位根检验方法解决了检验势不稳定以及原假设主观设置的问题,能够给出更全面稳健的单位根检验判断.
面板数据;贝叶斯方法;分位数;单位根;仿真
许多经济金融时间序列的建模方法都以经济平稳这一假设为基础,但在实际中,经济金融时间序列数据通常呈现出非平稳性,如利率、汇率或资产价格序列等,单位根检验是计量经济学中检验时间序列数据平稳性的最重要工具.随着面板数据的出现与不断发展,非平稳时间序列理论在面板数据体系下得以进一步开发与深化,面板单位根则是利用面板数据研究面板时间序列出具的非平稳特征,同时综合了截面维度和时间维度的数据信息,以进行更准确的单位根检验.
近年来,面板数据的动态特征研究,特别是围绕非平稳性检验进行的研究,受到诸多学者的关注.Shin和Jhee[1]利用带MTAR项的面板模型,首次研究了面板数据方面的非平稳动态非对称性问题.而Shin和Lee[2]则利用工具变量方法消除了误差项之间的截面相依,进行面板MTAR模型的单位根检验.Beyaert和Camacheo[3]研究了面板TAR模型的单位根检验,并用bootstrap方法考察了截面相依条件下的面板TAR单位根检验,并进行了面板指数平滑转换自回归(ESTAR)模型的单位根检验.与其类似的工作还有Cerrato等[4]和Chi-Keung[5]的相关研究,他们都是将Kapetanios等[6]的非线性单位根检验推广到面板背景下以检验面板中每个时间序列的平稳性.Chiang等[7]依据自回归参数和转换速度在各个个体间是一样还是不一样,并将ESTAR面板模型分为同质和异质,同时研究了同质性面板ESTAR和异质性面板ESTAR中的单位根检验,并应用到实际汇率数据中以检验购买力平价假说.
然而,这些面板单位根检验统计量的渐进性质主要依赖于个体数N和时期数T趋向无穷的假设,而实际应用中的面板数据的个体数和时期数一般都有限,从而导致面板单位根检验水平歪曲(size distortion)和检验势(power)不稳定的问题;同时,传统面板单位根是基于原假设为存在单位根或原假设为不存在单位根而进行的假设检验,因此,它是在原假设成立的条件下进行的假设检验过程,从而存在原假设设置的主观选择问题,影响了单位根检验的准确性.采用贝叶斯方法进行面板单位根检验能够解决检验势不稳定和原假设设置主观选择的问题,利用后验概率比来比较原假设和备择假设的可能性,从而获得更客观可靠的判断.因此,从贝叶斯角度研究面板单位根检验具有现实和理论意义.应用贝叶斯方法进行面板单位根检验分析的研究目前还极少,主要有Meligkotsidou等[8]研究了截面相依面板模型的贝叶斯单位根检验方法,并将其用于研究G-7国家的GDP面板数据问题;Jung和Shin[9]研究了面板数据MTAR模型的贝叶斯分析,并进行了非对称和单位根检验.本文在面板数据自回归模型的基础上,利用贝叶斯分位回归方法,设计MCMC抽样算法进行贝叶斯分位推断和贝叶斯分位单位根检验,并进行模拟实验研究.
1 模型结构分析
设Z为分布函数FZ的随机变量,τ为0和1之间的实数,记qZ(τ)为FZ的第τ分位数,从而有:
FZ(q)=τ.
即

(1)
qZ(τ)被称为Z的τ分位点,它完全刻画了随机变量Z的性质.Koenker和Bassett于1978年提出了分位回归方法,是对传统分位点方法的一种扩展.假设yit是一个面板时间序列变量,考虑如下自回归模型:
yit=α1i+φ1iyi,t-1+μit.
(2)

(3)
其中,假设误差项εit的τ分位数为0,φi=1表明yit服从单位根过程,|φi|<1表明yit是一个平稳序列;而φi>1则表示yit具有突增特性.
根据分位回归的思想,可以通过最小化非对称加权绝对离差得到分位自回归模型的参数估计,即
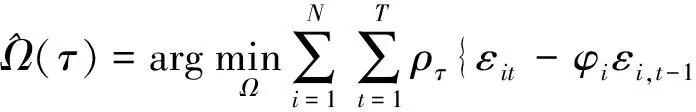
(4)
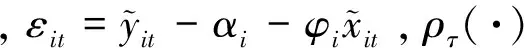
pAL(εit)=τ(1-τ)exp {-ρτ(εit)}.
(5)
其中,ρτ(·)的定义与前面一致.从而,很容易证明εit的τ分位数为0,均值与方差分别为:

2 贝叶斯分析
依据Kobayashi等[12]的观点,在贝叶斯框架中,为了利用Gibbs抽样算法进行模型估计,将假设误差项εit服从非对称Laplace分布的如下位置——尺度混合形式:
(6)
此处,ξ=(1-2τ)/(τ(1-τ)),θ2=2/[τ(1-τ)],且vit~exp (1)与uit~N(0,1)相互独立.从而,面板数据自回归模型对应的面板分位自回归模型变为:
(7)
如果设模型的参数空间为Θ(τ)=[αi(τ),φi(τ),vit(τ)]或者Θ,可以得到面板分位自回归模型的似然函数为:
(8)

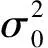
由于参数的联合后验分布与似然函数、先验分布的乘积成正比,所以,通过参数的先验分布设置可以得到参数相应的条件后验分布.设Θ-w表示参数空间Θ中除去w的其他参数的集合,下面讨论面板分位自回归模型参数的后验条件分布.
1)αi的完全条件后验分布.由条件概率的定义,∀i=1,2,…,N,参数αi的条件后验分布之间相互独立,则αi关于参数Θ-α的完全条件分布为:
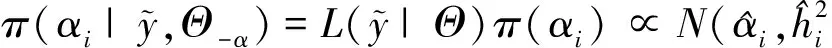
(9)
其中:
2)φi的完全条件后验分布.类似地,由条件概率的定义,∀i=1,2,…,N,自回归参数φi的条件后验分布之间相互独立,φi的完全条件后验分布为:
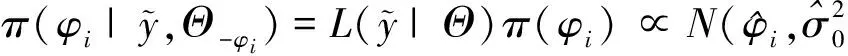
(10)
其中:
3)根据条件概率的定义,参数vit关于Θ-v=[αi(τ),φi(τ)]的完全条件后验分布可以看作服从广义逆高斯分布,即
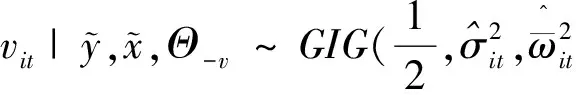
(11)
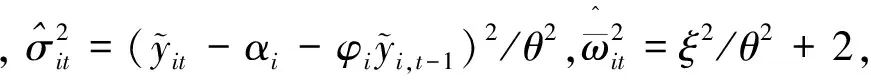
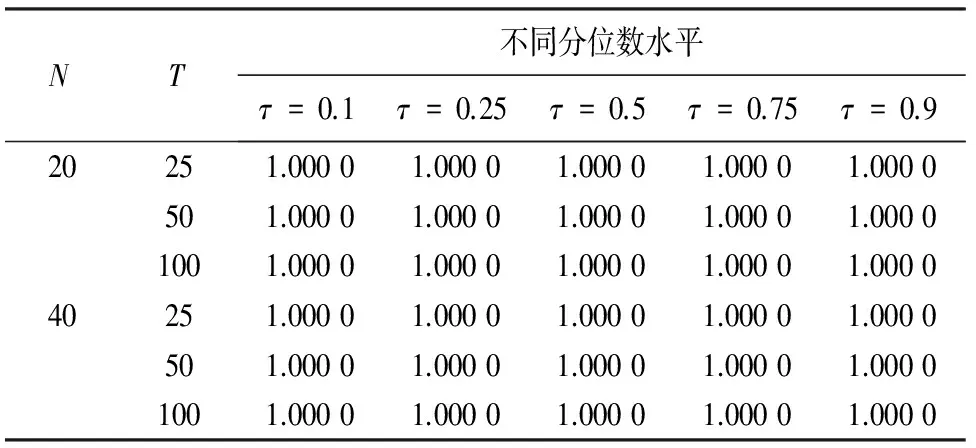
d2x)},x>0,-∞ (12) 在此,Kq(·)是第三类修正的Bessel函数. 面板数据单位根检验即是进行假设检验H0:φi=1↔H1:φi<1.在分位回归模型框架下,利用分位单位根检验方法进行单位根检验具有现实的意义,例如,在中位数水平下的单位根过程则意味着大多数个体服从单位根过程或者较少的个体具有单位根,因此,分位数水平下的检验是一个反应检验目的的更好选择.一般地,第τ分位水平下的单位根假设为H0:φi(τ)=1,如果-1<φi(τ)<1,则说明在第τ分位水平下yit是平稳过程.在此,主要考察中位数水平下的面板数据单位根检验,即对H0:φi(0.5)=1↔H1:φi(0.5)<1进行贝叶斯假设检验.在贝叶斯理论中,一般采用贝叶斯因子进行模型选择和假设检验,贝叶斯因子的计算一般比较复杂,通常需要通过边缘似然函数来计算贝叶斯因子;而对于嵌套模型,应用广义Savage-Dickey密度比(SDDR)计算贝叶斯因子使得计算简化,避免了计算每个假设下相应模型的边缘似然函数.在此,令单位根检验的贝叶斯因子为B10=P(H1|Data)/P(H0|Data),通过MCMC算法得到模型参数的后验分布的样本,利用这些样本获得参数的后验密度估计,从而可以计算贝叶斯因子以及各个假设的后验概率,以得到更加详细的后验判断. 重复步骤1~3,直至迭代分布收敛到参数的目标分布,Markov链达到平稳状态时则停止,为了消除初始值的影响,可以舍弃掉开始的若干次抽样,根据遍历性定理,从而可以用舍弃掉初始若干次抽样样本后的抽样序列,对面板数据自回归模型参数进行分位估计,并利用这些抽样样本计算贝叶斯因子和后验概率比,以检验面板时间序列在各个分位水平下的单位根性质. 由于贝叶斯假设检验可以看作一个贝叶斯决策问题,从而贝叶斯理论中常用贝叶斯因子和后验概率比进行模型选择和假设检验,如果有若干个假设{H0,H1,H2,…,Hs}可供选择,则可以利用现有数据,应用各个假设对应的模型对数据拟合的优劣进行比较来对这些假设进行检验.设Mi和Mj分别为假设Hi和Hj对应的模型,假设Hi和Hj条件下的参数分别为θi和θj,π(θi)和π(θj)分别为θi和θj的先验分布密度函数,也即分别代表先验模型概率π(Mi)和π(Mj),l(θi|x)和l(θj|x)分别为样本x=(x1,x2,…,xn)在Hi和Hj下的边缘似然函数,则假设Hi相对于假设Hj进行检验的后验概率比为: (13) π(M0|x)+π(M1|x)=1. (14) 从而可以得到假设H0和H1的后验概率为: π(H1|x)=π(M1|x)=1-π(M0|x). (15) 当假设Hi和Hj对应的模型的先验模型概率π(Mi)=π(Mj)时,先验概率比等于1,所以,后验概率比简化为边缘似然的比,即所谓的贝叶斯因子. 而在贝叶斯协整分析中,主要是应用贝叶斯因子、后验概率比来进行协整检验.贝叶斯因子的计算一般比较复杂,通常需要通过边缘似然函数来计算贝叶斯因子;而对于嵌套模型,应用广义Savage-Dickey密度比(SDDR)计算贝叶斯因子,使得计算简化,避免了计算每个假设下相应模型的边缘似然函数.在此,令协整检验的贝叶斯因子为B10=P(H1|Data)/P(H0|Data),通过MCMC算法得到模型参数的后验分布的样本,利用这些样本获得参数的后验密度估计,从而可以计算贝叶斯因子以及各个假设的后验概率. yit=α+φyi,t-1+εit. (16) 由MCMC算法可以得到各个参数的边缘后验分布,并且根据MCMC抽样可以计算出φ<1的后验概率.在模型运行过程中, 一共迭代了15 000 次,首先对每个参数进行5 000次迭代,进行退火,以保证参数的收敛性,然后舍弃原来的迭代,再进行10 000次迭代,用5 001次到15 000次迭代得到的MCMC样本来估计参数.表1给出了不存在单位根时的后验概率,即φ<1的后验概率.从表中结果可知,当φ=0.5,即序列平稳时,贝叶斯方法在不同分位数水平下不存在单位根的后验概率为1. 表1 贝叶斯分位单位根检验模型φ<1的后验概率 本文利用非对称Laplace分布结合面板数据自回归模型,构建贝叶斯框架下的面板数据分位自回归模型,并进行参数的贝叶斯分位推断,从而提出贝叶斯分位单位根检验方法.设计了MCMC抽样算法进行参数后验估计和不同分位数水平下的贝叶斯单位根检验,解决了贝叶斯方法在应用中遇到的高维数值计算问题.在此基础上,通过 Monte Carlo模拟实验分析了贝叶斯分位单位根检验方法的有效性和可行性,发现贝叶斯分位单位根检验能够提供更加稳健的单位根检验判断.因此,在对面板时间序列进行分析时,贝叶斯分位单位根检验方法能够克服传统面板数据单位根检验方法中检验势不稳定的缺陷,同时可以避免单位根检验由于原假设设置主观选择导致的检验偏误问题,进而为实际经济管理问题中面板时间序列非平稳性的判断提供更加稳健全面的信息和决策指导. [1] SHIN D W, JHEE W. Tests for asymmetry in possibly nonstationary dynamic panel models[J]. Economic Letters, 2006, 91:15-20. [2] SHIN D W, LEE O. Unit root tests for panel MTAR model with cross-sectionally dependent error[J]. Metrika, 2008, 67:315-326. [3] BEYAERT A, CAMACHEO M. TAR panel unit root tests and real convergence[J]. Review of Development Economics, 2008, 12(3):668-681. [4] CERRATO M, DE PERETTI C, SARANTIS N. A nonlinear panel unit root test under cross section dependence[D].Glasgow: Department of Economics, University of Glasgow, 2009. [5] CHI-KEUNG M L. Convergence across the United States: evidence from panel ESTAR unit root test[J]. International Advances in Economic Research, 2010, 16(1):52-64. [6] KAPETANIOS G, SHIN Y, SNELL A. Testing for a unit root in the nonlinear STAR framework[J]. Journal of Econometrics, 2003, 112:359-379. [7] CHIANG M H, KUAN C M, LO C H. Panel unit root test under smooth transition[D].Tainan: Institute of International Business, National Cheng Kung University, 2007. [8] MELIGKOTSIDOU L, TZAVALIS E, VRONTOS I D. A Bayesian analysis of unit roots in panel data models with cross-sectional dependence[EB/OL]. Available at SSRN: http://ssrn.com/abstract=1334766, 2009. [9] JUNG Y Y, SHIN D W S. Bayesian analysis of panel data using an MTAR model[J]. Journal of Applied Statistics, 2005, 32(8): 841-854. [10]YU K, MOYEED R A. Bayesian quantile regression[J]. Statistics & Probability Letters, 2001, 54(4): 437-447. [11]曾惠芳,朱慧明,李素芳,等.基于MH算法的贝叶斯分位自回归模型[J].湖南大学学报:自然科学版,2010,37(2):88-92. ZENG Hui-fang, ZHU Hui-ming, LI Su-fang,etal. Bayesian inference on the quantile autoregressive models with metropolis-hastings algorithm[J]. Journal of Hunan University :Natural Sciences, 2010, 37(2):88-92. (In Chinese) [12]KOBAYASHI G, KOZUMI H. Bayesian analysis of quantile regression for censored dynamic panel data[J]. Computational Statistics, 2012, 27(2):359-380. [13]LUBRANO M. Testing for unit roots in a Bayesian framework[J]. Journal of Econometrics, 1995, 69(1): 81-109. [14]BAUWENS L, LUBRANO M, RICHARD J F. Bayesian inference in dynamic econometric models, advanced texts in econometrics[M]. New York: Oxford University Press,1999:41. [15]UHLIG H. What macroeconomists should know about unit roots: a Bayesian perspective[J]. Econometrics Theory, 1994, 10(3/4):645-671. [16]BURGETTE L F, REITER J P. Modeling adverse birth outcomes via confirmatory factor quantile regression[J]. Biometrics, 2012, 68(1):92-100. Bayesian Unit Root Tests in Panel Data by Using MCMC Algorithm LI Su-fang1,2†, ZHU Hui-ming1, LI Rong1 (1. College of Business Administration, Hunan Univ, Changsha, Hunan 410082, China; 2. School of Statistics and Mathematics, Zhongnan Univ of Economics and Law, Wuhan, Hubei 430073, China) Because the test power of the traditional panel unit root tests is unstable and the choice of the null hypothesis of traditional panel unit root tests is subjective, this paper proposed a Bayesian quantile unit root test for panel data based on asymmetric Laplace distribution. On the basis of quantile autoregression panel data model, the full conditional distributions of parameters were inferred and MCMC algorithm was designed. And then, Bayesian quantile unit root tests were conducted. Numerical results were produced via a combination of Monte Carlo simulation, from which we find that Bayesian quantile unit root tests are noticeably efficient and feasible. As a result, it is shown that Bayesian quantile unit root tests solve unstable power problems and the subjective choice of the null hypothesis. Furthermore, the tests are more robust and can provide more complete information. panel data; Bayesian methods; quantile; unit root; simulation 1674-2974(2015)01-0136-05 2013-09-30 国家自然科学基金资助项目(71301166),National Natural Science Foundation of China(71301166);教育部人文社会科学青年项目(13YJC910007);中国博士后科学基金资助项目(2013M540623,2014T70766);2013年中南财经政法大学基本科研业务费青年教师创新项目(2013084);中南财经政法大学引进人才科研启动金项目(31541211204) 李素芳(1983-),女,湖南邵阳人,湖南大学博士后,博士,讲师†通讯联系人,E-mail: bbs8.8@163.com O212.8 A3 MCMC算法
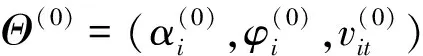
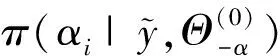

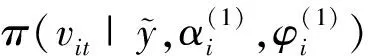
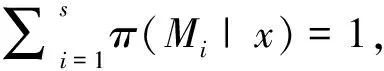
4 模拟分析
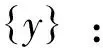

5 结 论
