瓜柱柱脚直榫节点受弯力学模型研究

陈春超,邱洪兴,包轶楠

(东南大学 混凝土及预应力混凝土结构教育部重点实验室，江苏 南京 210096)

瓜柱柱脚直榫节点受弯力学模型研究

陈春超,邱洪兴†,包轶楠

(东南大学 混凝土及预应力混凝土结构教育部重点实验室，江苏 南京 210096)

为了研究古木结构中瓜柱柱脚直榫节点的受弯性能，设计了3个不同尺寸的缩尺试件模型.通过单调加载试验，获得了节点的弯矩-转角关系以及最终破坏形态.运用大型有限元分析软件，采用实体单元对节点的受弯性能进行数值模拟.结合试验研究和数值模拟结果，在一定简化假定的基础上建立了节点受弯时的简化力学模型.研究结果表明：瓜柱柱脚直榫节点的主要破坏类型为脱榫破坏；受弯时节点的抵抗力矩主要由柱顶轴压力对转动点来合成；节点的弯矩-转角曲线可以简化为带下降段的双折线模型.

木结构；卯节点；受弯性能；弯矩-转角关系；力学模型

榫卯节点是古木结构的关键部位，其受力状态也极为复杂.榫卯节点的构造决定了其承载力低于试件承载力，是结构中的薄弱部位.历次震害[1]也表明，木构架的破坏多发生在榫卯连接处.由于榫卯节点为半刚性节点，其弯矩-转角关系是进行整体结构分析的基础.因此从榫卯节点的受弯性能入手，对古木结构进行研究具有重要意义.

乐志[2]结合现代结构理论和试验研究建立了馒头榫、管脚榫与尺寸、材性、缝隙等参数相关的受弯承载力理论公式.姚侃等[3]通过力学分析和低周反复荷载试验，拟合出了燕尾榫节点弯矩-转角的三折线恢复力模型.李琪[4]对透榫、半榫、燕尾榫进行了静力分析，针对各种可能出现的破坏形态推导了强度计算公式.王俊鑫[5]通过分析燕尾榫节点的受力状态，基于试验研究，建立了弯矩与转角的四参数幂函数模型.徐明刚[6]在机理分析的基础上，建立了循环加载下节点弯矩-转角关系的理论模型.Chang等[7]对榫卯连接进行了有限元分析，根据有限元结果拟合出了榫卯连接的初始刚度计算公式.Shanks等[8]对传统的橡树燕尾榫卯节点进行试验研究，获得了节点的抗拉、抗弯和抗剪刚度及极限承载力.Han等[9]对韩国传统木结构榫卯连接模型进行了试验研究，结果表明榫卯的刚度和屈服荷载随榫接触面的增加而提高.

目前关于榫卯节点力学模型的研究，多是对缩尺构件试验结果的拟合，具有较大的局限性，且研究对象主要集中在燕尾榫节点上.本文以瓜柱柱脚直榫节点为研究对象，在试验研究的基础上结合数值模拟对节点的受弯性能进行了较深入的理论研究，初步建立了该节点受弯时的简化力学模型.

1 试验研究

1.1 试件的设计与制作

瓜柱柱脚直榫位于与梁架垂直相交的瓜柱柱脚，在抬梁式古木结构中广泛使用.参考清工部《工程做法则例》按1∶1.76和1∶1.30的缩尺比例设计了3个不同尺寸的瓜柱柱脚直榫节点，编号分别为GZ1, GZ2和GZ3.材料为中国古建筑木结构中常见的杉木，部分实测材性参数详见表1，试件模型如图1所示.

表1 实测材性参数

注：Ec,L,Ec,R和Ec,T分别为木材纵向、径向和弦向抗压弹性模量；fc,L,fc,R和fc,T分别为纵向、径向和弦向抗压强度；GLR,GLT和GRT分别为径切面、弦切面和横切面剪切模量，单位均为N/mm2.

1.2 加载方案

试验在东南大学结构试验室进行，加载装置如图2所示(为了便于加载，将试件在平面内旋转180°).其中滑车用于使千斤顶随着柱顶的侧移而水平移动，从而保证竖向荷载始终作用在柱顶的中心位置.试件所受竖向荷载按照真实结构荷重[10]结合缩尺比例，在柱顶施加10 kN轴压力.采用位移控制加载，第一级位移幅值为5 mm，以后每增加5 mm作为下一级控制位移，单调加载直至试件破坏.

(a) GZ1，GZ2

(b) GZ3

图2 加载装置示意图

定义柱底端与梁边的相对转角为节点转角θ，通过位移计1和2读数之差与2个位移计水平距离的比值测定；位移计3用于控制位移加载，并且可以对转角进行校核.

1.3 试验现象及试验结果

瓜柱柱脚直榫试件在加载不久即出现轻微的木纤维压紧的“吱”“吱”声，继续加载试件发出清脆的木材挤紧滑移的“嗝”“嗝”声，水平推力迅速上升并很快到达峰值点.此后2种声音混杂出现且音量逐渐变大，榫头被缓慢拔出，水平推力随着控制位移的增大而近似线性下降，节点逐渐进入倾覆状态，试验结束.榫头和卯口基本保持原状，梁表面对应榫肩处有显著压痕，这表明竖向荷载主要由榫头两侧的榫肩部位直接传递给梁.3个试件均为拔榫破坏，部分破坏形态如图3所示.

图3 试件破坏形态

图4给出了试验所得的瓜柱柱脚直榫节点单调加载弯矩-转角关系曲线.从图中可以看出瓜柱柱脚直榫节点的弯矩-转角曲线包括上升段和下降段，两者均近似线性变化，其中上升段的斜率较陡，转角很小时弯矩就达到了峰值点；此后弯矩随着转角增加而逐渐缓慢下降至零，节点进入倾覆状态.

转角/rad

2 数值模拟

本文利用大型有限元分析软件ABAQUS对瓜柱柱脚直榫的受弯状态进行数值模拟，建模时采用八节点六面体线性减缩积分格式的三维实体单元(C3D8R)．该单元对位移的求解结果较精确，网格存在扭曲变形时，分析精度也不会受到较大影响，并且在弯曲荷载作用下不容易发生剪切自锁.

将木材简化成正交异性材料，顺纹和横纹(径向和弦向)受拉采用单折线本构模型，受压采用双折线本构模型，且受拉弹性模量等于受压弹性模量，如图5所示.运用Engineering Constants定义材料弹性阶段的力学常数，塑性阶段采用等向弹塑性模型，满足Hill屈服准则.在此基础上导入field函数，定义了木材抗压时有塑性变形，而抗拉时无塑性变形的特点.同时调用ABAQUS中自带的potential函数，定义了木材不同方向的初始屈服应力.

图5 横纹应力-应变关系

榫头和卯口之间的作用，法向采用硬接触(“hard” contact)来模拟，切向采用静动摩擦模型(Static-Kinetic friction formulation)来处理.接触面上切向作用力与相对滑动速度的关系：在一定压力N下，当接触面的切向作用力f小于临界力fs时，两接触间处于相对静止状态(sticking condition)，当切向作用力大于临界力fs(如公式(1)所示)时，两接触之间就发生相对滑动，且摩擦因数随着两接触面之间的相对滑动按指数衰减，如式(2)和图6所示.

fs=μsN,

(1)

(2)

式中：μs为静摩擦因数，本文中取为0.33[11]；μk为动摩擦因数，本文中取0.26[11]；dc为摩擦因数衰减系数，本文中取为3.0[12]；γeq为滑动速度.

图6 指数衰减摩擦模型

有限元模型的单元划分和节点变形、应力状态如图7所示.从图7(a)可以看出柱顶竖向荷载主要由榫肩部位直接传递至梁上表面，这与试验研究的结论是一致的；从图7(b)中可以看出转动过程中榫头的转动点近似为柱右侧和梁上表面的交点o，榫头左侧A处为主要挤压变形区域.

(a) 单元划分

(b) 节点变形和S33方向应力状态

GZ1，GZ2试件数值模拟所得节点的单调加载曲线与试验结果对比见图8，二者趋势基本相同，但也存在一定差异，这主要是由于下列原因导致的：

1) 数值模拟中木结构单元采用ABAQUS里的线性减缩积分单元C3D8R，这种单元本身就使得模拟结构刚度偏大.

2) 木材离散性较大，存在一定的初始缺陷和加工误差.

转角/rad

基于以上原因，数值模拟与试验结果之间的差异是可接受的，该数值模拟方法能够较好地模拟瓜柱柱脚直榫节点的受力状态，具有一定的可信性.

3 理论分析

3.1 基本假定

在建立节点理论模型时，结合试验研究和数值模拟结果采用如下简化假定：

1) 榫头转动点为柱右侧与梁上表面交点o，如图9所示.

2) 卯口内榫头的弯曲、剪切变形可以忽略，即认为榫头在卯口内仅发生刚体运动[6]，从而榫头各点位移和挤压变形可由节点转角θ和几何关系确定.

3) 榫头和卯口接触处若一方为顺纹受压、另一方为横纹受压，则挤压变形全部发生在横纹受压的一方.

4) 不考虑木材局部受压导致的强度和弹性模量的提高，挤压处木材横纹受压的应力-应变关系采用图5所示本构模型.

3.2 几何条件

柱顶轴压力、弯矩分别为N和M；摩擦因数为μ；榫长、榫宽、榫高、梁高、柱长分别用l，a，h，H和L表示.榫卯节点的变形状态如图9所示.

lA=δAcotθ．

图9 节点变形状态

3.3 平衡条件

瓜柱柱脚直榫节点的受力状态如图10所示，其中A处的挤压力用FA表示，作用点位于应力分布图的形心，相应的摩擦力用fA表示.N为作用在柱中心线的竖向荷载，xN为N作用点到o点的水平距离：

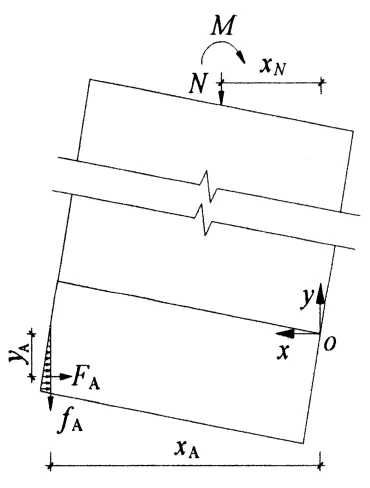
图10 节点受力状态

对坐标原点o取矩，根据节点的力矩平衡条件可得弹性阶段：

M=FAyA+fAh+NxN.

(3)

3.4 物理条件

1) 弹性阶段

挤压处的最大挤压应力：

各力的表达式如下：

fA=μFA．

挤压部位的力臂：

xA=h，

yA=2lA/3．

2) 弹塑性阶段

进入塑性后，挤压处的变形图由三角形变为梯形，则：

挤压部位的力臂：

3.5 受弯性能

取μ=0.26[11]，将GZ1和GZ2的相应尺寸和材性参数代入式(3)可得瓜柱柱脚直榫节点弯矩-转角全过程理论曲线，如图11所示.与试验结果相比二者下降段的趋势基本相同，但在上升段却存在一定差异.这主要是因为在加载过程中，千斤顶与柱侧的挤压接触面上会产生轻微局压变形，柱也存在微小的弯曲和剪切变形，在理论推导时这些因素全部被忽略，因此试验曲线在加载初期有一段斜率很大的上升段，而理论曲线的起点却位于纵坐标上，且峰值点和破坏点对应的转角也比试验值的略小.

转角/rad

图12显示瓜柱柱脚直榫节点的抵抗力矩主要由柱顶轴压力来合成，榫卯之间挤压接触面上的局部压应力和摩擦力合成的抵抗力矩也起一定作用.图中点1为榫头A处木材挤压由弹性进入塑性的临界点，点2为弯矩-转角理论曲线的峰值点，点3为破坏点.由图可见点1和点2对应的转角值基本相同，点1和点3对应的弯矩值也很接近.

转角/rad

为了使理论公式简便、实用，根据上述分析做出如下简化假定：

1) 榫头A处木材挤压由弹性进入塑性时的转角即为弯矩-转角理论曲线峰值点对应的转角.

2) 榫头A处木材挤压进入塑性后由局部压应力和摩擦力合成的抵抗力矩大小始终保持不变，即点1和点3的连线与横坐标平行.

3) 由于转角较小，可近似取cosθ=1，sinθ=θ.

基于上述简化假定，由式(3)可得峰值点坐标和破坏点坐标.

峰值点坐标：

(4)

破坏点坐标：

(5)

结合试验研究、数值模拟和理论分析可将瓜柱柱脚直榫节点的弯矩-转角曲线近似简化为带下降段的双折线模型，如图13所示.曲线以A点作为转折点，其中A点既是屈服点也是峰值点(θm，Mm)，定义此时榫头木材挤压由弹性进入塑性；B点为破坏点(θu，Mu)，定义此时节点承载力降低到零，瓜柱即将倾覆.A和B两点的坐标可以由式(4)和(5)求得.

转角/rad

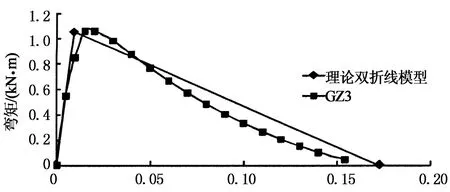
将GZ3的相应尺寸和材性参数代入式(4)和(5)可得其简化理论双折线模型，如图14所示.与试验结果相比二者趋势基本相同，吻合较好，这表明该简化双折线模型能够较好地模拟瓜柱柱脚直榫节点的受弯性能，具有一定的可信性.

转角/rad

4 结 论

通过对瓜柱柱脚直榫节点进行试验研究、数值模拟和理论分析，可以得到以下结论：

1) 瓜柱柱脚直榫节点的主要破坏类型为脱榫破坏，破坏时榫头和卯口基本保持完好.

2) 节点的抵抗力矩主要由柱顶轴压力来合成，榫头和卯口挤压接触面上的局部压应力和摩擦力合成的抵抗力矩也起一定作用.

3) 节点的弯矩-转角曲线可以简化为带下降段的双折线模型.

[1] 杨亚弟,杜景林,李桂荣.古建筑震害特性分析[J].世界地震工程,2000, 16(3): 12-16.

YANG Ya-di, DU Jing-lin, LI Gui-rong. Analysis of the earthquake disaster characteristics of ancient building structures [J]. World Information on Earthquake Engineering, 2000, 16(3): 12-16.(In Chinese)

[2] 乐志. 中国传统木构架榫卯及侧向稳定研究[D]. 南京:东南大学土木工程学院, 2004: 28-33.

YUE Zhi. The study of traditional wooden rabbet & traditional structure horizontal stability [D]. Nanjing: College of Civil Engineering, Southeast University, 2004: 28-33. (In Chinese)

[3] 姚侃, 赵鸿铁, 葛鸿鹏. 古建木结构榫卯连接特性的试验研究[J]. 工程力学, 2006, 23(10): 168-173.

YAO Kan, ZHAO Hong-tie, GE Hong-peng. Experimental studies on the characteristic of mortise-tenon joint in historic timber buildings [J]. Engineering Mechanics，2006, 23(10): 168-173. (In Chinese)

[4] 李琪. 古建筑木结构榫卯及木构架力学性能与抗震研究[D]. 西安:西安建筑科技大学土木工程学院, 2008: 35-53.

LI Qi. Study of rabbets and mechanical properties and seismic performance of timber frame of Chinese historic timber buildings [D]. Xi’an: School of Civil Engineering, Xi’an University of Architecture and Technology, 2008: 35-53.(In Chinese)

[5] 王俊鑫. 榫卯连接木结构的静力与动力分析研究[D]. 昆明: 昆明理工大学建筑工程学院, 2008: 25-32.

WANG Jun-xin. Static and dynamic analysis of mortise-tenon connection timber structure [D]. Kunming: Faculty of Civil and Architectural Engineering, Kunming University of Science & Technology, 2008: 25-32. (In Chinese)

[6] 徐明刚. 中国古建筑木结构榫卯节点抗震性能研究[D]. 南京: 东南大学土木工程学院, 2011: 76-89.

XU Ming-gang. Study of aseismatic behavior of mortise-tenon joints in Chinese ancient timber buildings [D]. Nanjing: College of Civil Engineering, Southeast University, 2011: 76-89. (In Chinese)

[7] CHANG W S, HSU M F, CHEN C J. Estimating rotational stiffness of timber joints by using fractional factorial experiments combined with computer simulation [C]//Proceedings of the 8th World Conference on Timber Engineering. Lahti: WCTE, 2004: 101-106.

[8] SHANKS J, WALKER P. Testing of traditional connections in Green oak carpentry [C]//Proceedings of the 8th World Conference on Timber Engineering. Lahti: WCTE, 2004: 183-186.

[9] HAN S R, LEE J J. Mechanical performance of Korean traditional wooden building of the column-girder tenon-joint by joint type [C]//Proceedings of the 9th World Conference on Timber Engineering. Portland: WCTE, 2006: 23.

[10]王天. 古代大木作静力初探[M]. 北京：文物出版社, 1992: 159-178.

WANG Tian. Static analysis on ancient timber structures [M]. Beijing: Cultural Relics Publishing House, 1992: 159-178. (In Chinese)

[11]孟庆军. 木质材料间摩擦性能及其对木结构设计的影响研究[D]. 哈尔滨: 东北林业大学, 2010:85.

MENG Qing-jun. The study for frictional properties of wooden materials and the impact on wood structure design [D]. Harbin: Northeast Forestry University, 2010:85. (In Chinese)

[12]陈志勇. 应县木塔典型节点及结构受力性能研究[D]. 哈尔滨: 哈尔滨工业大学土木工程学院, 2011:193-195.

CHEN Zhi-yong. Behaviour of typical joints and the structure of Yingxian wood pagoda [D]. Harbin：School of Civil Engineering, Harbin Institute of Technology, 2011:193-195. (In Chinese)

Study on the Flexural Mechanical Model of Straight Mortise-tenon Joints in the Base of Melon-column

CHEN Chun-chao, QIU Hong-xing†, BAO Yi-nan

(Key Laboratory of Concrete and Prestressed Concrete Structures of the Ministry of Education, Southeast Univ, Nanjing, Jiangsu 210096, China)

Three straight mortise-tenon joints in the base of melon-column were built to study their flexural behavior. The relationships of moment-rotation and failure modes were obtained through monotonic loading tests. The flexural behavior was simulated with finite element software. On the premise of some basic assumptions, the simplified mechanical model was built on the basis of experiments and numerical simulation. Research results show that the main damage type of joints is pulling out, and the resisting torque is mainly synthesized by the vertical load on the top of columns to rotation point. The moment-rotation curve can be simplified as a double broken line model.

timber structures; mortise-tenon joints; flexural behavior; moment-rotation relationship; mechanical model

1674-2974(2015)03-0050-07

2014-04-23

国家十二五科技支撑计划项目(2012BAJ14B02)

陈春超(1988-)，男，江苏淮安人，东南大学博士研究生

†通讯联系人，E-mail:101000854@seu.edu.cn

TU366．2

A