铝合金板式节点面外初始弯曲刚度的杆件间交互影响

郭小农,熊 哲†,罗永峰,徐 晗

(1.同济大学 建筑工程系,上海 200092;2.中天建设集团 浙江钢构有限公司,浙江 杭州 310008)

铝合金板式节点面外初始弯曲刚度的杆件间交互影响

郭小农1,熊 哲1†,罗永峰1,徐 晗2

(1.同济大学 建筑工程系,上海 200092;2.中天建设集团 浙江钢构有限公司,浙江 杭州 310008)

铝合金板式节点具有良好的整体刚度性能，其面外初始弯曲刚度的杆件间交互影响不容忽视.本文在现有研究的基础上，定义了铝合金板式节点面外弯曲刚度矩阵.为进行深入研究，对铝合金板式节点进行有限元模拟.以节点板厚度、节点板半径、杆件高度和螺栓数量为参数，建立14个节点模型，分析关于节点面外弯曲刚度的杆件间交互影响.根据有限元结果，提出计算杆件交互影响程度的理论公式.和有限元结果的比较表明，公式的计算精度高，具有良好的适用性.

铝合金；板式节点；弯曲刚度；杆件间交互影响；有限元

铝合金板式节点是铝合金空间网壳结构中最为常用的节点形式之一.板式节点是通过不锈钢螺栓将上下两块圆形节点板和H型杆件的翼缘紧密连接而成的，每个节点通常连接6根杆件并大致呈中心对称形状.节点外形美观、造型新颖、具有良好的整体刚度[1].

现有研究表明，节点刚度对网壳结构稳定承载能力具有不容忽视的影响[2].因此，空间结构的节点刚度已成为当今建筑结构领域的热点研究问题之一.曾银枝等[3]对铝合金板式节点网壳进行研究，指出网壳分析时，应考虑节点刚度的影响.张竟乐等[4]对铝合金板式节点刚度进行数值模拟，提出节点刚度计算公式.文献[5-8]通过14个铝合金板式节点试验，研究了铝合金板式节点的承载能力和面外弯曲刚度性能.其研究表明，板式节点在加载初期具有良好的整体刚度性能，加载后期则呈现出明显的非线性性能.文献[5-8]对铝合金板式节点刚度的研究仅仅是针对单根杆件进行的，忽略了杆件之间的相互影响.然而，由于多根杆件连接在同一块节点板上，因此各杆件之间的作用主要通过节点相互传导，节点刚度必然受到杆件间的交互影响，其影响程度不容忽视.

针对上述情况，本文拟对铝合金板式节点弯曲刚度的杆件间交互影响进行理论分析和数值模拟.首先，为反映节点面外弯曲刚度的杆件间交互影响，定义节点刚度矩阵.然后建立铝合金板式节点有限元模型，对节点刚度的杆件间交互影响进行单参数分析.最后根据数值模拟结果和数据回归方法，提出杆件交互影响程度的公式.

1 理论分析

铝合金板式节点汇交的杆件较多，各杆件的局部弯曲变形不仅由其自身荷载引起，同时还受其他杆件变形的影响.王伟[9]在对K形钢管相贯节点的研究中指出，一根杆件的局部变形将会引起另外一根杆件的局部变形，为准确地反映该变形机制，必须定义节点刚度矩阵.

对于铝合金板式节点(如图1所示)，其面外弯曲刚度对结构性能影响最为显著.因此，本文重点对铝合金板式节点面外初始弯曲刚度矩阵进行研究.根据结构力学原理，6杆连接的铝合金板式节点(如图2所示)面外弯曲刚度矩阵为：

(1a)式中: 元素kij为由杆件Lj(j=1,2,…,6)的杆端截面与节点中心的相对单位转角φj引起杆件Li(i=1,2,…,6)的杆端截面弯矩Myi(图2中弯矩所示方向为正，即弯矩使上节点板受拉为正).根据刚度矩阵的定义，各杆件杆端截面弯矩和转角之间的关系可表达为：

(1b)

图1 铝合金板式节点图

图2 铝合金板式节点杆件编号

大部分铝合金板式节点为6杆连接且中心对称(或近似中心对称).根据铝合金板式节点的对称性和互等定理，矩阵[K]L可以用kφ0,kφ1,kφ2和kφ3四个代表元素表示，且：

k11=k22=k33=k44=k55=k66=kφ0,

(2a)

k12=k23=k34=k45=k56=k61=

k21=k32=k43=k54=k65=k16=kφ1,

(2b)

k13=k24=k35=k46=k51=k62=

k31=k42=k53=k64=k15=k26=kφ2,

(2c)

k14=k25=k36=k41=k52=k63=kφ3.

(2d)

则矩阵[K]L可以写成：

(3)

在有限元模型中，若单独对杆Li施加单位转动，会引起节点的整体转动变形，进而导致各杆端截面与节点中心均存在相对转角，无法直接求得[K]L各代表元素.为方便用有限元模型计算kφ0～kφ3，本文采用对柔度矩阵求逆的方法来求刚度矩阵，即：

(4)

其中柔度矩阵[f]L可写为：

(5)

柔度矩阵中元素fij可定义为：由杆件j的单位杆端弯矩Myi引起杆件i杆端截面与节点中心的相对转角φj.在有限元模型中对杆件Li单独施加杆端弯矩Myi，并计算得到各杆端转角φj.则有

(6)

根据对称性，[f]L也可以类似地通过fφ0,fφ1,fφ2和fφ3四个代表元素表示，即：

(7)

求出柔度矩阵元素fij后，即可组装得到节点的柔度矩阵，再对其求逆，可得到节点刚度矩阵[K]L.

根据式(3)可以看到，刚度矩阵的主对角元kφ0代表了某杆件位置板式节点的面外刚度，而kφ1代表相邻杆件对节点刚度的影响，kφ2代表次相邻杆件对节点刚度的影响，kφ3代表相对杆件对节点刚度的影响.定义：

α1=kφ1/kφ0,

(8a)

α2=kφ2/kφ0,

(8b)

α3=kφ3/kφ0.

(8c)

则这3个参数分别代表了相邻杆件、次相邻杆件和相对杆件对某杆件处板式节点的面外刚度的影响程度，即杆件交互影响因子.若上述α1,α2和α3均为零，则代表杆件之间没有相互影响.引入参数α1,α2和α3后，式(3)可以写成：

(9)

2 有限元模拟

2.1 有限元模型简介

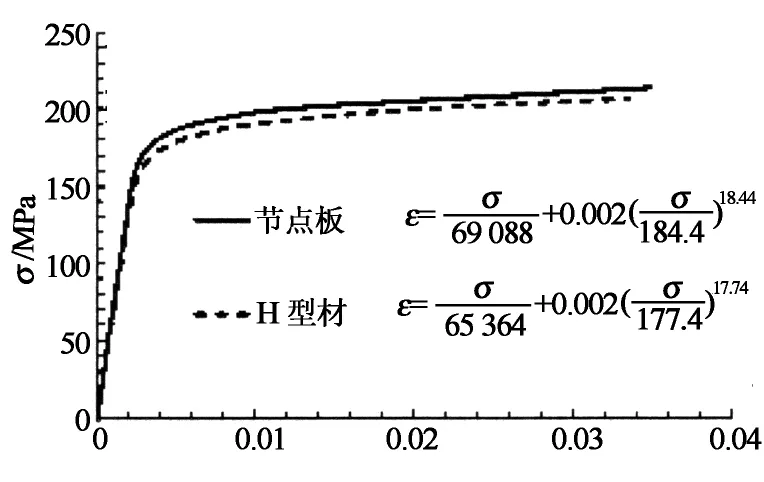
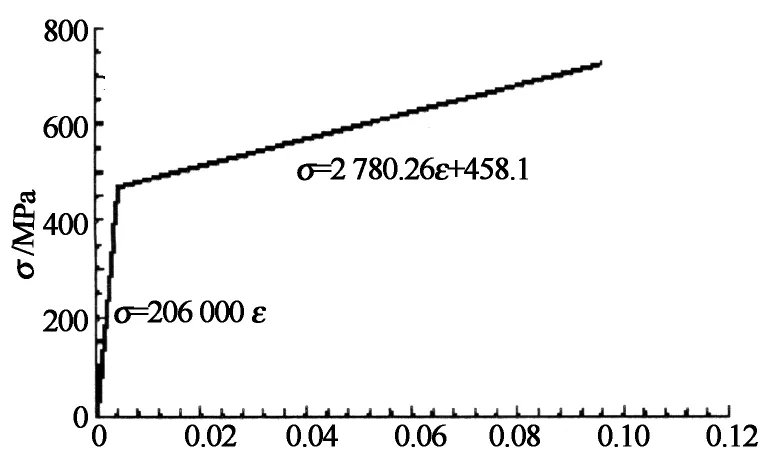
为进行深入研究，本文采用ABAQUS软件建立铝合金板式节点有限元(FE)模型.为提高计算效率，建立半节点体模型，如图3所示.有限元模型采用线性减缩积分单元C3D8R模拟.为减小因采用线性单元引起的计算误差，需要对部件分块划分单元，使螺栓孔附近应力集中区域单元较为精密和规律，如图4所示.为真实反映螺栓连接，模型考虑了螺栓与孔壁间隙的影响.模型中，所有螺栓的预紧力假设相等.模型中各部件的相互联系通过接触对实现，螺栓与节点板和翼缘板件的摩擦因数参考《铝合金结构设计规范》(GB 50429)[10]，取0.3.通过参考点对单根杆件施加弯矩.在节点板断面上施加对称约束.铝合金型材和节点板的材质均为6063-T5，其本构关系采用Ramberg-Osgood模型及SteinHardt建议[11](如图5所示)；不锈钢螺栓的牌号为A2-70，本构关系采用双折线模型(如图6所示).有限元模型中，铝合金和不锈钢的力学性能参数均采用文献[5]的拉伸试验数据，详见表1.文献[7]通过试验验证指出，该模型能够有效模拟铝合金板式节点的初始刚度.

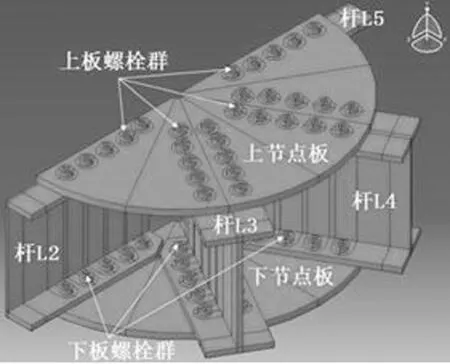
图3 半节点体模型

图4 模型的网格划分

表1 材料性能

应变ε

应变ε

2.2 参数分析

以节点板厚度t, 节点板半径R, 螺栓数量n及杆件截面高度h为变化参数，建立4个系列共计14个铝合金板式节点有限元模型.其具体参数如图7和表2所示，其中p1为最内排螺栓横向间距，p2为其他排螺栓横向间距，R0为最内排螺栓到圆板中心的距离，Rc为圆板中心域半径，g1为最内排螺栓与其相邻排螺栓纵向间距，g2为其他相邻排螺栓纵向间距，ge为最外排螺栓到圆板边缘距离.为求出柔度矩阵的代表元素，模型仅对单根杆件施加弯矩，其余杆件外端自由.

分析计算各系列有限元模型.根据节点杆端截面的变形结果及公式(6)，求出节点柔度矩阵，并求逆得到相应的节点刚度矩阵.表3给出了各系列模型的柔度矩阵与刚度矩阵的元素.图8给出了刚度矩阵元素随各几何参数的变化曲线.图9给出了杆件交互影响因子随各几何参数的变化.

图7 数值模型参数示意图

表2 数值模型参数

观察分析表3,图8和图9，可归纳出以下结论：

1)当对单根杆件施加弯矩时，其相邻杆件转角为正、次相邻杆件和相对杆件的转角为负，并且相对杆件的转角绝对值最大.其主要原因在于，对于整个节点体，其约束设置于节点中心点.当对单根杆件施加使杆件向下转动的弯矩时，节点将会以节点中心点为支点发生变形.参考各杆件的局部坐标，假设转角以杆件向下转动为正，则相邻杆件发生正转角、次相邻杆件和相对杆件发生负转角，并且相对杆件发生的转角最大.

表3 弯曲柔度矩阵与刚度矩阵元素值

图8 刚度矩阵元素值随各参数的变化情况

2)节点板厚度对板式节点初始弯曲刚度有影响.节点板厚度越大，初始弯曲刚度越大.其主要原因在于节点板厚度的增加提高了节点板的抗弯刚度，进而使得节点刚度变大.节点板厚度对杆件交互影响因子有很大影响.节点板厚度增大，杆件交互影响因子减小.其主要原因在于当节点板变厚时，节点板的面外刚度变大，此时，相同弯矩下，节点板的变形变小，故杆件所在节点板区域的变形对节点板其他区域的影响变小.显然，当节点板面外刚度无限大时，节点板将无面外变形，杆件间的交互影响因子为零.

3)改变节点板半径对节点初始弯曲刚度和杆件交互影响因子均无显著影响.

4)杆件截面高度对节点初始弯曲刚度有很大影响.杆件截面变高直接增加了杆件的抗弯刚度，从而提高了节点初始弯曲刚度.但是杆件截面高度不能影响节点板的面外抗弯刚度，从而对杆件交互影响因子无显著影响.

5)增加螺栓数量能够提高节点的初始弯曲刚度.增加螺栓数量会增强杆件的交互影响.螺栓数量越多，其节点板面外刚度削弱越多，导致杆件间交互影响程度增强.

图9 杆件交互影响程度随各参数的变化情况

3 拟合公式

表3给出了杆件交互影响因子α1,α2和α3的数值，其平均值分别为-0.053，0.079和0.108.从以上分析可以看出：1)杆件交互影响因子随着节点板厚度t的增大而减小，当节点板厚度无限大时，杆件交互影响程度为零.节点板的面外刚度随着圆板中心域半径Rc的增大而减小，因此杆件交互影响因子随着圆板中心域半径Rc的增大而增大.故可假设杆件交互影响因子与t/Rc呈指数变化；2)如图9(d)所示，杆件交互影响因子随着螺栓数量的增加而变大，故杆件交互影响因子也可假设与螺栓数量呈指数变化.故根据最小二乘法原理[12]，得到杆件交互影响程度公式如下：

(10a)

(10b)

(10c)

式(10)的计算结果和有限元结果的比较见表4.从表4可以看出，理论公式与有限元结果的误差平均值分别为2.6%，2.9%和2.7%，理论公式与有限元结果(FER)比较接近，验证了理论公式的适用性.

4 结 论

铝合金板式节点刚度具有良好的整体性能，其杆件间的交互影响不容忽视.本文对铝合金板式节点刚度的杆件间交互影响进行研究，主要结论如下：

1)在理论分析的基础上，确定了考虑杆件交互影响的节点面外弯曲刚度的矩阵.

2)建立了计算铝合金板式节点面外初始刚度的有限元模型，分析了节点板厚度、节点板半径、杆件高度和螺栓数量对节点面外初始刚度的影响.结果表明节点板厚度、杆件截面高度和螺栓数量均对节点面外初始刚度有影响.其中，节点板厚度越大，初始弯曲刚度越大；杆件截面越高，初始弯曲刚度越大；增加螺栓数量能够提高节点的初始弯曲刚度.

3)分析了节点板厚度、节点板半径、杆件高度和螺栓数量对杆件交互影响程度的影响.结果表明节点板厚度和螺栓数量对其有较大的影响.一方面，节点板厚度增大，杆件交互影响因子减小；另一方面，杆件交互影响因子随着螺栓数量的增加而变大.

4)杆件交互影响因子可由公式(10)计算.与数值结果的比较表明，公式具有较高的精度和适用性，可为铝合金板式节点刚度的设计提供参考依据.

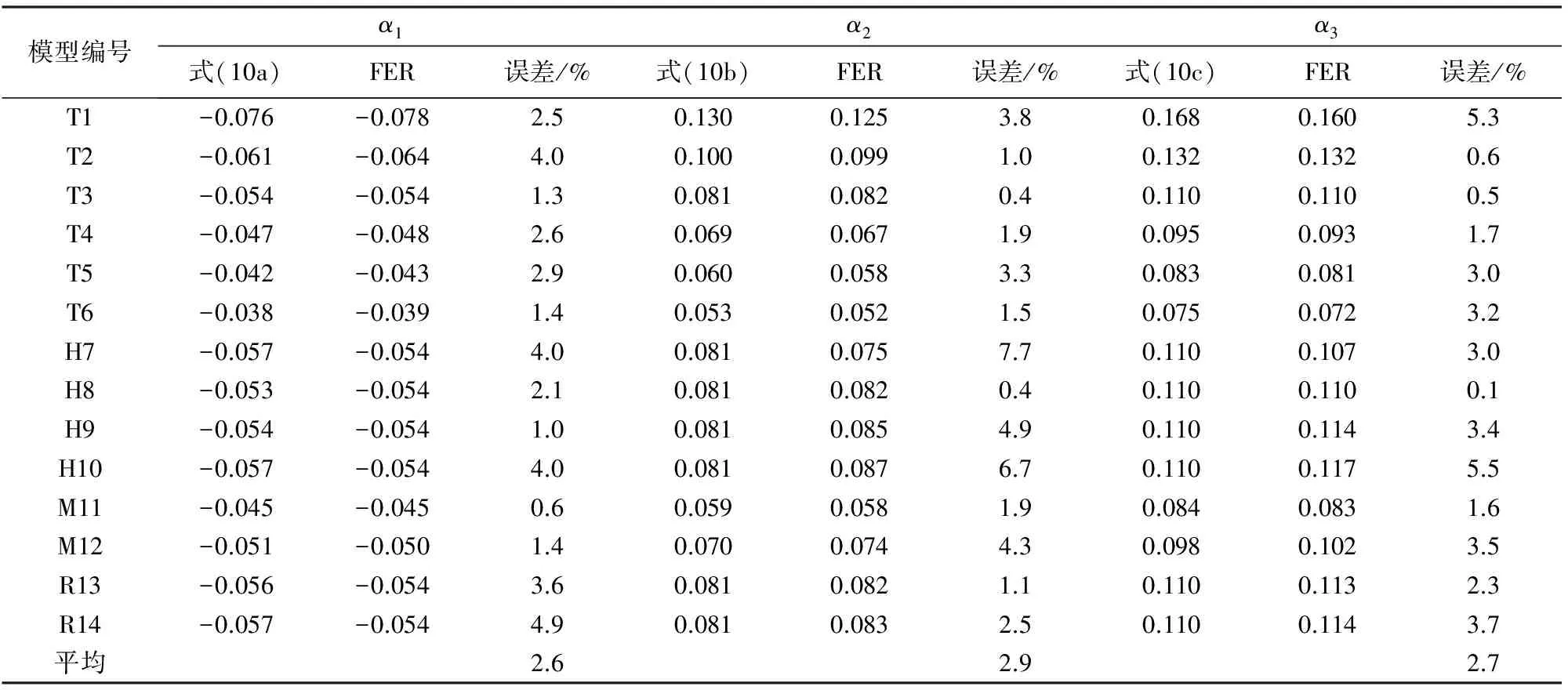
表4 理论结果和有限元结果的比较

[1] 郭小农, 熊哲, 罗永峰. 空间网格结构节点刚度研究现状简述[J]. 结构工程师, 2014, 30(4): 185-195.

GUO Xiao-nong, XIONG Zhe, LUO Yong-feng. State-of-the-arts of research on the joint stiffness of the spatial structures [J]. Structural Engineers, 2014, 30(4): 185-195. (In Chinese)

[2] FAN F, MA H H, CAO Z G,etal. A new classification system for the joints used in lattice shells[J]. Thin-Walled Structures, 2011, 49(12):1544-1553.

[3] 曾银枝, 钱若军, 王人鹏, 等. 铝合金穹顶的试验研究[J]. 空间结构, 2000, 6(4):47-52.

ZENG Yin-zhi, QIAN Ruo-jun, WANG Ren-peng,etal. Test research on the aluminous-alloy dome[J]. Spatial Structures, 2000, 6(4):47-52. (In Chinese)

[4] 张竟乐, 赵金城, 许洪明. 单层网壳板式节点的刚度分析[J]. 工业建筑, 2005, 35(4):88-90.

ZHANG Jing-le, ZHAO Jin-cheng, XU Hong-ming. Analysis of stiffness of gusset-type joints for single-layer reticulated shells[J]. Industrial Construction, 2005, 35(4):88-90. (In Chinese)

[5] 郭小农, 熊哲, 罗永峰, 等. 铝合金板式节点承载性能试验研究[J]. 同济大学学报: 自然科学版, 2014, 42(7): 1024-1030.

GUO Xiao-nong, XIONG Zhe, LUO Yong-feng,etal. Experimental research on load-bearing behavior of aluminum alloy gusset joint [J]. Journal of Tongji University: Natural Science, 2014, 42(7): 1024-1030. (In Chinese)

[6] 郭小农, 熊哲, 罗永峰，等. 铝合金板式节点弯曲刚度理论分析[J]. 建筑结构学报，2014, 35(10): 144-150.

GUO Xiao-nong, XIONG Zhe, LUO Yong-feng,etal. Theoretical study on bending stiffness of aluminum alloy gusset joint[J]. Journal of Building Structures, 2014, 35(10): 144-150.(In Chinese)

[7] 郭小农, 熊哲, 罗永峰, 等. 铝合金板式节点初始刚度[J]. 同济大学学报:自然科学版, 2014, 42(8): 1161-1166.

GUO Xiao-nong, XIONG Zhe, LUO Yong-feng,etal. Initial bending stiffness of aluminum alloy gusset joint [J]. Journal of Tongji University: Natural Science, 2014, 42(8):1161-1166. (In Chinese)

[8] 郭小农, 邱立秋, 罗永峰, 等. 铝合金板式节点受弯承载力试验研究[J]. 湖南大学学报: 自然科学版, 2014, 41(4):47-53.

GUO Xiao-nong, QIU Li-qiu, LUO Yong-feng,etal. Experimental research on the bending capacity of aluminum alloy gusset joints [J]. Journal of Hunan University:Natural Sciences, 2014, 41(4):47-53. (In Chinese)

[9] 王伟, 陈以一. 圆钢管相贯节点局部刚度的参数公式[J]. 同济大学学报: 自然科学版, 2003, 31(5):515-519.

WANG Wei, CHEN Yi-yi. Parametric formulas for local rigidity of unstiffened tubular joints[J]. Journal of Tongji University: Natural Science, 2003, 31(5):515-519. (In Chinese)

[10]GB 50429—2007 铝合金结构设计规范[S]. 北京:中国计划出版社, 2008:122.

GB 50429—2007 Code for design of aluminum structures[S]. Beijing: China Planning Press, 2008:122. (In Chinese)

[11]郭小农, 沈祖炎, 李元齐，等. 国产结构用铝合金材料本构关系及物理力学性能研究[J]. 建筑结构学报, 2007, 28(6):110-117.

GUO Xiao-nong, SHEN Zu-yan, LI Yuan-qi,etal. Stress-strain relationship and physical-mechanical properties of domestic structural aluminum alloy [J]. Journal of Building Structures, 2007, 28(6): 110-117. (In Chinese)

[12]贾小勇, 徐传胜, 白欣. 最小二乘法的创立及其思想方法[J]. 西北大学学报: 自然科学版, 2006, 36(3): 507-511.

JIA Xiao-yong, XU Chuan-sheng, BAI Xin. The invention and way of thinking on least squares[J]. Journal of Northwest University: Natural Science Edition, 2006, 36(3): 507-511. (In Chinese)

The Out-of-plane Initial Bending Stiffness Interaction of Members on the Aluminum Alloy Gusset Joint

GUO Xiao-nong1, XIONG Zhe1†, LUO Yong-feng1, XU Han2

(1.Dept of Building Engineering, Tongji Univ, Shanghai 200092, China；

2.Zhongtian Construction Group Zhejiang Steel Structure CO, LTD, Hangzhou, Zhejiang 310008,China)

The aluminum alloy gusset joint has a good global stiffness performance, so the out-of-plane initial bending stiffness interaction of members cannot be neglected. Based on the existing research, the matrix for the bending stiffness of aluminum alloy gusset joint was defined, and the finite element (FE) analysis was developed. Fourteen FE models of aluminum alloy gusset joint were established to discuss the bending stiffness interaction of members, taking into account the thickness of plate, the radius of plate, the height of member’s cross-section and the number of bolts. According to the FE results, the theoretical formulae to estimate the bending stiffness interaction of members on the aluminum alloy gusset joint were proposed. Making a comparison of the theoretical results with FE results, the theoretical results have a good agreement with the FE results, which verifies the applicability of the proposed formulae.

aluminum alloy； gusset joint; bending stiffness; interaction of members；finite element

1674-2974(2015)03-0036-07

2014-04-23

国家自然科学基金资助项目(50908168，51478335)，National Natural Science Foundation of China(50908168,51478335)

郭小农(1977-)，男，四川成都人，同济大学副教授，博士

†通讯联系人，E-mail:123superpanda@tongji.edu.cn

TU395

A