近场地震作用下锈蚀钢筋混凝土桥墩的IDA分析

陈昉健，易伟建

(湖南大学 土木工程学院，湖南 长沙 410082)

近场地震作用下锈蚀钢筋混凝土桥墩的IDA分析

陈昉健，易伟建†

(湖南大学 土木工程学院，湖南 长沙 410082)

利用锈蚀钢筋混凝土柱的滞回试验结果，验证钢筋混凝土构件中锈蚀模型的正确性；利用钢筋混凝土框架的振动台试验结果，验证用OPENSEES程序进行钢筋混凝土结构非线性动力分析的可行性.在此基础上，从PEER地震数据库中选取了30条地震记录，采用OPENSEES建立弹塑性有限元动力分析模型，对钢筋锈蚀的钢筋混凝土桥墩在远场地震、近场非脉冲地震和近场脉冲地震作用下的性能进行非线性时程分析，研究桥墩柱在三类地震作用下的反应，以及钢筋锈蚀对结构地震响应的影响.针对近场脉冲地震对结构进行增量动力分析(Incremental dynamic analysis, IDA)，得到结构的IDA曲线和近场地震作用下钢筋锈蚀对结构抗震性能的影响.分析结果表明，在考虑钢筋锈蚀因素时，近场脉冲地震对结构抗震性能影响最为显著，在结构抗震设计中应引起注意.

钢筋锈蚀；钢筋混凝土桥墩；OPENSEES；近场地震；增量动力分析

混凝土中的钢筋锈蚀是钢筋混凝土结构使用周期中存在的一个普遍问题，是影响结构耐久性和安全性的重要因素.特别是对于处在海洋环境下和寒冷地区的混凝土桥梁结构，由于海水和除冰盐中氯离子的存在，混凝土开裂现象普遍存在，桥墩表面出现纵向锈蚀裂缝、受力钢筋断裂、钢筋骨架局部严重损坏等问题都严重影响桥梁结构的使用寿命和整体安全.钢筋锈蚀主要表现为纵向受力钢筋锈蚀，局部箍筋锈蚀甚至断裂以及钢筋骨架的局部锈蚀损坏.这些将会使混凝土产生沿纵筋发展的锈胀裂缝、降低甚至使箍筋失去约束作用、导致混凝土保护层剥落、构件承载力降低，直至危及整个结构的受力安全.例如，加拿大蒙特利尔市迪克森大街的立交桥，1959年建成，由于冻融循环影响和除冰盐的使用，造成桥底板钢筋严重锈蚀，1994年即由于桥底板混凝土严重分层停止使用，于1999年拆除[1].我国1980年建成的北京西直门立交桥，由于长期使用除冰盐，仅使用20年就使得部分梁柱锈蚀严重甚至危及桥梁结构安全，已于1999年拆除重建[2].

处在地震区的桥梁结构，同时受到钢筋锈蚀和地震灾害的威胁，因此有必要研究锈蚀钢筋混凝土构件的抗震性能，以评价其结构的抗震安全性，避免其在地震时发生倒塌破坏.汪梦甫[3]在研究中提到，断层距R≤15 km的地震属于近场地震；震级M≥5.6级，原始记录PGA≥0.2 g，PGV≥20 cm/s的地震，动力脉冲效应显著，对结构震害形成影响较大.因此，很有必要考虑结构在不同类型地震作用下的响应.

目前，国内外虽然也进行过不少关于锈蚀柱抗震性能的试验研究[ 4- 6]，但主要集中在矩形截面的钢筋混凝土柱，对于桥梁结构中大量使用的圆截面柱很少涉及.贡金鑫等[7]是为数不多的进行了钢筋锈蚀圆柱抗震性能试验的学者，构件也仅限于较小的尺寸(圆柱直径260 mm)，与实际工程中桥墩柱的尺寸规模有较大差距.由于对试验设备的要求较高，大尺寸桥墩柱的往复荷载试验往往很难进行，更不用说振动台试验，因此，采用非线性分析软件对这类构件进行模拟计算成为了一种有效的研究手段.

本文以钢筋混凝土桥墩柱为对象，通过非线性动力时程分析和增量动力分析，得到了桥墩柱在钢筋锈蚀前后的地震响应，为发生钢筋锈蚀的桥墩抗震性能评估提供理论依据.

1 锈蚀钢筋混凝土构件的模拟

对于钢筋锈蚀在钢筋混凝土构件和结构中的普遍性及危害性，国内外的很多学者已经做了大量研究，形成了一些共识.Tuutti[8]发现，钢筋表面聚集高浓度氯离子的位置将发生局部锈蚀，即“坑蚀”，而混凝土的碳化是大多数均匀锈蚀产生的原因，这是钢筋锈蚀最主要的两种形式.

1.1 混凝土中钢筋锈蚀的影响

钢筋混凝土构件中钢筋的锈蚀情况，通常采用钢筋平均质量损失率或平均截面损失率作为评估指标.由于坑蚀所产生锈坑的分布无规律，测量比较困难，故通常利用钢筋的质量损失作为锈蚀程度的评价标准.由此得到的钢筋平均质量损失率相当于将锈蚀按照均匀锈蚀考虑，在这个前提下，钢筋的平均质量损失可以等效于其平均截面损失.

在布雷西亚大学(University of Brescia)结构工程试验室完成的锈蚀钢筋受拉试验结果的基础上，Cairns等[9]进行了性能参数研究，定性地得到了钢筋主要力学性能参数随锈蚀率变化的基本规律，如图1所示.

平均截面损失/%

图1显示，随着平均截面损失(即锈蚀因素的影响)的增大，锈蚀钢筋的极限拉应力减小.锈蚀钢筋的名义屈服强度随锈蚀程度的增加而降低，但其下降幅度小于极限强度.而钢筋的抗拉强度受其最小截面控制，因此强度的下降比其平均截面的下降更为迅速.同时，锈蚀钢筋延性的下降又比强度的降低更显著.

锈蚀钢筋的强度变化，可由以下经验公式表示[9]：

(1)

(2)

式中：fy,fu分别表示屈服强度和极限抗拉强度，基于原始截面；fy0，fu0分别表示未锈蚀钢筋的屈服强度和极限受拉强度；αy，αu为经验系数.文献[9]对10组不同学者所做试验的结果进行了统计分析，发现αy的平均值为0.01.通常情况下，αy或αu的值取0.01代表均匀锈蚀；超过0.01则反映非均匀锈蚀的影响.Du等[10]建议取αy=0.005.为了既不过分削弱钢筋的锈蚀后性能，又能考虑到坑蚀相对于均匀锈蚀的严重性，本文取αy=0.015.

1.2 钢筋锈蚀模型验证

本文采用非线性有限元软件OPENSEES[11]对文献[7]中的锈蚀钢筋混凝土圆柱往复荷载试验结果进行模拟.使用非线性梁柱单元(nonlinearbeam-columnelement)中基于位移的单元(DisplacementBasedBeam-ColumnElement) 建模，该单元基于位移方程且考虑沿单元长度方向的塑性分布.将柱截面划分为一系列非弹性纤维单元，同时将单根柱构件沿柱高划分为多个计算单元，在柱底部塑性铰形成区域单元节点间距减小，上部区域节点间距较大.

分析模型的混凝土材料选用Concrete02，该材料基于修正后的Kent-Park模型[12]，可以通过调整混凝土受压骨架曲线的峰值应力、峰值应变和线性受拉软化阶段的斜率来反映箍筋的约束作用，也考虑了混凝土的剩余强度.钢筋本构模型采用Giuffré-Menegotto-Pinto的Steel02单轴模型[13]，通过钢筋应变强化率的取值，考虑钢筋的各向同性应变强化，并通过参数调整在一定范围内控制钢筋从弹性阶段向塑性阶段的过渡形状.柱截面约束区混凝土利用Mander[14]提出的公式对混凝土强度进行调整.在柱底添加零长度截面单元(Zero-LengthSectionElement)，模拟应变渗透效应，配合使用单轴滑移材料模型(Bond-SP01)[15]来考虑混凝土柱受力过程中端部锚固钢筋黏结滑移效应引起的变形.

文献[6]中各试件纵筋的锈蚀率采用的是各根钢筋锈蚀率的平均值，因此，在分析时，假设同一试件中每根纵向钢筋受到的锈蚀损伤相同，且锈蚀沿柱周边和柱高均匀分布.试验中，箍筋锈蚀比纵筋严重，分析时，取箍筋的锈蚀率在纵筋基础上提高50%.在钢筋锈蚀后，钢筋与混凝土之间将出现一层锈蚀产物，严重影响两者之间的黏结强度.因此，对钢筋锈蚀试件模型中的滑移材料参数进行修改，其中$b表示单调滑移条件下，钢筋应力在屈服后的初始强化比，在钢筋完好时取0.5，考虑锈蚀后，滑移量将显著增加，在此取为0.3.参数$R表征的是往复荷载下，钢筋应力响应中的捏缩现象，钢筋完好时，滞回曲线丰满，该值取为0.8，考虑锈蚀后，滞回曲线将出现明显的捏缩，因此将该值取为0.5.计算结果与试验荷载-位移滞回曲线的比较如图2所示，因试验构件数量较多，此处仅给出部分模拟结果.

构件编号形式为Cx-y，C表示构件为圆柱截面，x表示构件钢筋锈蚀率(质量损失率)百分比的整数部分，y表示试验轴压比的小数部分.

从图2中可以看到，对锈蚀钢筋的参数选取，反映到计算结果中与试验结果基本吻合.试验中，钢筋锈蚀率和轴压比增大后，对柱保护层有明显的削弱，而这在OPENSEES的建模中难以在不改变构件模型的情况下得到体现.因此在对锈蚀率和轴压比较高的构件进行模拟计算时，需要进行处理，即改变构件的截面直径，在保证核心区不变的同时，缩小保护层厚度，以此减小计算模型的构件刚度.模拟结果表明，这样引入钢筋锈蚀影响是合理的，可用于后续计算中.

2 地震作用分析模型

为验证OPENSEES进行地震荷载模拟计算的有效性和正确性，对文献[16]中2个单层双跨钢筋混凝土框架试件的振动台试验结果进行模拟.该框架试件的中柱为方柱，为试验主要研究对象，两根边柱为圆柱，主要起支撑上部荷载的作用，试验主要目的是得到中柱在地震波作用下的性能响应.2个试件的尺寸和配筋完全一致，区别仅在于试件1的中柱轴压比为0.1，试件2的中柱轴压比为0.24.

此处建模选用的单元类型和材料模型都与上一节的相同，以保证2种建模思路的统一和逻辑上的一致性.模拟计算得到的中柱层间位移角随地震波变化曲线与试验结果的对比如图3所示.

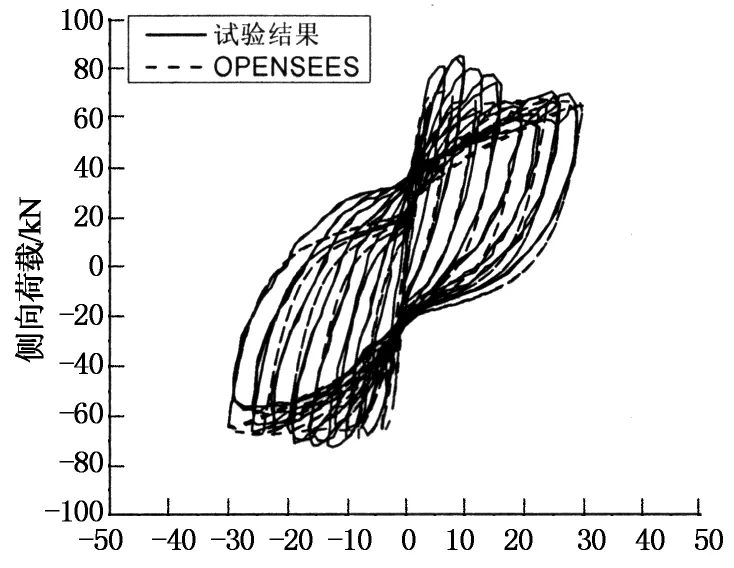
侧向位移/mm

侧向位移/mm

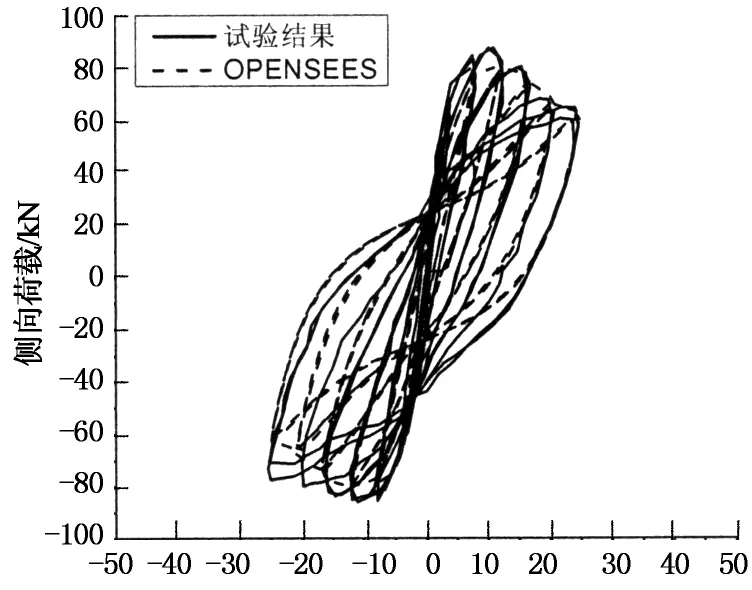
侧向位移/mm

侧向位移/mm

从图3的曲线对比可知，计算模型可以较为准确地反映出构件在地震荷载作用下的基本性能.模拟分析的结果是令人满意的，这样的建模方法可以用于地震荷载下钢筋混凝土桥墩的性能分析.

时间/s

时间/s

3 算例与地震动的选取

3.1 算例信息

对于桥梁结构，通常要求在地震荷载下，桥梁上部结构处于弹性状态.而实际震害资料也显示，一般上部结构不会发生破坏.因此，本文仅选取桥墩作为地震荷载IDA分析的研究对象.

选取参考文献[17]中，按我国桥梁规范设计的圆截面桥墩为分析模型，模型示意图见图4.桥墩高6.0 m，墩柱外径为1 000 mm，保护层厚度为50 mm，采用C30混凝土.纵向钢筋为24根直径为36 mm的HRB400级钢筋，箍筋采用直径12 mm的HRB335钢筋，间距为100 mm.上部结构传递的重力荷载为3 150 kN，在建模时，该荷载作为集中荷载施加于模型顶部节点.引入钢筋混凝土构件中钢筋的锈蚀影响时，按锈蚀率10%和20%两种情况考虑.

图4 墩柱模型示意图

3.2 地震动的选取

在进行IDA分析时，选取10 ～ 20条地震波记录就能满足一定的精度要求，以文献[18]附录A中列举的符合中国场地类别的地震波为参考，从PEER数据库中选取了30条地震波.其中20条断层距小于10 km的近场地震波记录，分为两组.Loh等[19]指出，峰值地面速度与峰值地面加速度之比(PGV/PGA)是识别近震效应的主要特征，当PGV/PGA>0.2 s时，近震对结构的效应明显.因此，选取PGV/PGA > 0.2的10条地震波为一组，属于近场脉冲记录，另一组地震波PGV/PGA<0.2，属于近场非脉冲记录.此外，还选取了断层距大于30 km的10条远场记录.选用的地震波震级分布在5.23～7.62之间，假设桥墩属于Ⅱ类场地条件.

4 计算结果与分析

4.1 损伤指标的确定

在桥梁结构中，墩柱的变形能力直接影响到桥梁的抗震性能和上部结构的稳定.墩柱在地震荷载下的侧向变形可以直观地反映出桥墩在地震中的性能状态.因此，本文选取墩柱的墩顶侧移比作为判别桥墩在地震荷载中性能变化的损伤指标，其定义为整个地震过程中，墩顶的最大绝对位移与桥墩高度之比.文献[20]中给出了墩顶侧移比的定义式，如公式(3)[20]：

(3)

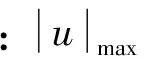
4.2 地震荷载计算结果

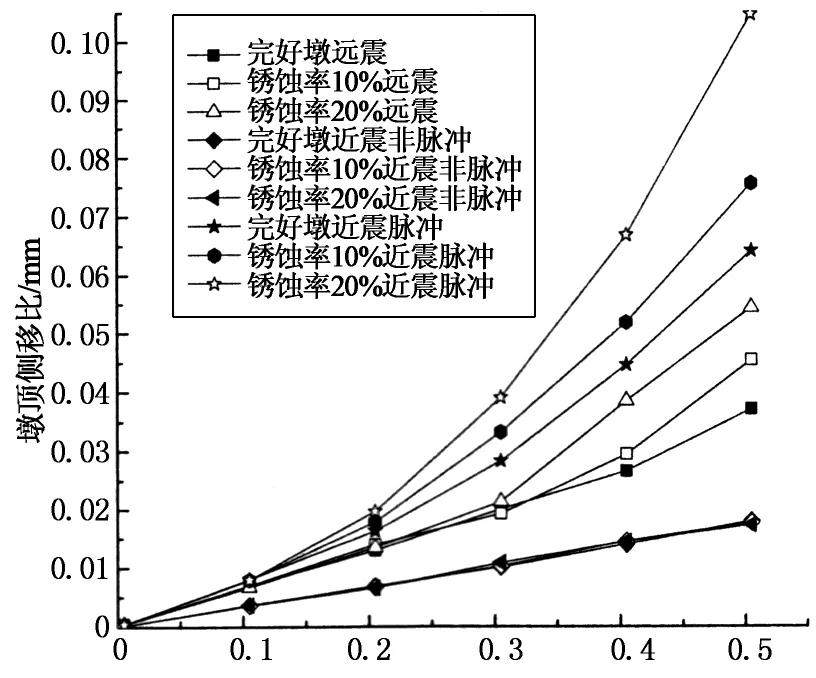
为了模拟逐渐从多遇地震调幅至罕遇地震，在进行时程分析时，对选用的地震波加速度峰值进行了调整，从0.005 g按0.1 g的步长增量逐渐增加到0.505 g.分别对完好状态下的桥墩模型和钢筋锈蚀率达到10%和20%时的桥墩模型进行分析.其中，模型构件锈蚀率的影响，按照本文第一节中介绍的方式予以考虑.计算对应不同地震动加速度峰值水平的结构顶点位移最大值(图5)，取3组地震波中10条记录的平均结果进行比较.

计算结果表明，远场地震和近场非脉冲地震相比，墩顶侧移比可以增加一倍左右，而近场脉冲地震与远场地震相比，随着峰值加速度(PGA)的增加，墩顶侧移比最多增加近80%.在近场非脉冲地震的作用下，钢筋锈蚀对桥墩变形的影响不明显.但另外两种地震类型下，钢筋锈蚀对桥墩变形的影响非常显著，锈蚀率对墩顶侧移比的影响随着PGA的增大而增大.

加速度峰值PGA/g

其中，10%的锈蚀率将使墩顶侧移比增大15%左右，20%的锈蚀率将使墩顶侧移比增大40%左右，并且随着PGA增大，这种变形的增长还有加大的趋势.值得注意的是，近场脉冲地震作用下，墩柱受锈蚀影响非常突出，变形增加幅度远高于另外两种地震类型.

5 IDA分析

地震荷载的作用时间、荷载强度和空间效应具有很大的随机性，造成结构的抗震性能具有明显的不确定性.增量动力分析(Incremental Dynamic Analysis，简称IDA)方法[21]通过系数调整地震动加速度值，来获得一组强度不同的地震动记录，输入结构模型后进行非线性时程分析.这种方法考虑到了结构抗震需求和承载能力的不确定性和随机因素，因此，对结构在不同性能水准下的抗震能力可以做出较为合理的评价.

选用对结构影响最剧烈的15条近场脉冲地震记录，主要来自1999年台湾集集地震和1994年发生在美国洛杉矶的北岭地震，对墩柱进行IDA分析，以进一步研究钢筋锈蚀对结构的影响.对计算得到的IDA曲线进行三阶样条插值拟合，得到了在墩柱完好，钢筋锈蚀率达到10%和20%时，墩顶最大位移随峰值-地面加速度变化IDA曲线如图6所示.

墩顶最大位移/mm(a) 完好墩柱

墩顶最大位移/mm(b) 锈蚀率10%墩柱

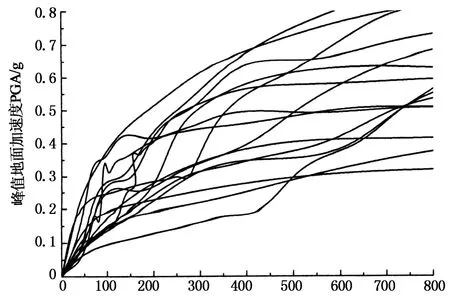
墩顶最大位移/mm(c) 锈蚀率20%墩柱

从图中可以看出，除了在PGA<0.1 g时，墩柱基本表现为弹性状态外，随着地震作用逐渐加大，大多数墩顶最大位移的IDA曲线呈现出了屈服后的水平段，而没有出现明显水平段的曲线，其形态也产生了显著的变化，这种变化的差异与地震波的随机性有关.

在引入了钢筋锈蚀这一影响因素后，可以看到出现屈服平台的曲线在更低的地震荷载水平发生屈服，而不出现屈服平台的曲线其斜率也逐渐减小.这意味着构件在更低的地震荷载水平发生了更大的变形，即构件在更早的时间点便趋近于倒塌，这显然对整体结构安全是很不利的.

以地震强度指标PGA作为控制参数，对15条近场脉冲地震的IDA曲线进行统计，所得的16%，50%，84%分位的IDA曲线如图7所示.

可以发现，在锈蚀因素的影响下，结构的3条分位IDA曲线的形态都产生了明显的变化，其总体趋势都表现为在更低的PGA作用下产生更大的位移.例如在墩顶最大位移达到300 mm(墩顶侧移比d=0.05)时，完好墩柱50%分位线对应的PGA约为0.45 g，而锈蚀率10%的墩柱约为0.39 g，锈蚀率20%的墩柱约为0.34 g.这意味着，在钢筋锈蚀的影响下，结构所能承受的地震荷载下降，相应地，在相同的地震荷载下，结构发生更严重破坏的概率提高，安全风险增加.

墩顶最大位移/mm(a) 完好墩柱

墩顶最大位移/mm(b) 锈蚀率10%墩柱

墩顶最大位移/mm(c) 锈蚀率20%墩柱

6 结 论

本文利用已有的锈蚀后钢筋性能变化模型，能够在一定程度上模拟出钢筋混凝土墩柱在钢筋锈蚀后的力学性能变化.但是对于锈蚀造成的钢筋与混凝土之间黏结的影响只考虑到了端部锚固区，沿构件方向钢筋与混凝土共同工作时的黏结强度变化，暂时难以进行模拟，在今后的研究中应进一步完善.通过以上对锈蚀钢筋混凝土墩柱的抗震性能分析可知，锈蚀将对结构的抗震性能产生较大的影响，具体结论如下：

1)对于3类典型地震作用， 除近场非脉冲地震外，钢筋锈蚀都增大了桥墩的顶点最大位移，并且这种影响随着PGA的增大而增加，其中又以近场脉冲地震的影响更为显著.

2)近场非脉冲地震受到钢筋锈蚀的影响不明显，而远场地震和近场脉冲地震对结构的作用，在钢筋锈蚀后产生了显著的加强.同样的地震荷载下结构由于钢筋锈蚀而增加的变形大大超过10%，足以说明这一影响因素完全不能忽视.因此，在对结构进行弹塑性分析和设计验算时，应适当地考虑钢筋锈蚀这一因素.

3)通过统计控制参数，得到IDA分位曲线，可以更加清晰地判断不同地震强度下结构的损伤情况和结构在达到某一破坏程度时抗震承载力的大小.

4)近场地震作用下，钢筋锈蚀显著改变了墩柱结构的IDA结果，使结构在更低的地震荷载水平便发生更大的变形，更趋近于破坏.在设计长期使用且有可能发生钢筋锈蚀的桥梁结构时，应对此引起特别的注意.

[1] PALSSON R, MIRZA M S. Mechanical response of corroded steel reinforcement of abandoned concrete bridge[J]. ACI Structural Journal, 2002, 99(2): 157-162.

[2] 王媛俐, 姚燕. 北京西直门旧桥混凝土破坏原因分析[M]//重点工程混凝土耐久性的研究与工程应用. 北京: 中国建筑工业出版社, 2001: 5-11.

WANG Yuan-li, YAO Yan. Analysis of the reason for Beijing Xizhimen bridge concrete failure[M]//Durability Research and Engineering Application on Key Project Concrete. Beijing: China Architecture & Building Press, 2001: 5-11.(In Chinese)

[3] 汪梦甫, 汪帜辉, 唐毅. 近场脉冲型地震对结构非弹性位移比谱的影响[J]. 湖南大学学报:自然科学版, 2014, 41(6): 9-15.

WANG Meng-fu, WANG Zhi-hui, TANG Yi. Influence of near-fault pulse-type ground motions on inelastic displacement ratio spectra[J]. Journal of Hunan University: Natural Sciences, 2014, 41(6): 9-15． (In Chinese)

[4] LEE H S, KAGE T , NOGUCHI T,etal. An experimental study on the retrofit ting effects of reinforced concrete columns damaged by rebar corrosion strengthened with carbon fiber sheets[J]. Cement and Concrete Research, 2003, 33(4): 563-570.

[5] RODRIGUEZ J, ORTEGA L M, CASAL J. Load carrying capacity of concrete structures with corroded reinforcement[J]. Construction and Building Materials, 1997, 11(4): 239-248.

[6] 史庆轩, 牛荻涛, 颜桂云. 反复荷载作用下锈蚀钢筋混凝土压弯构件恢复力性能的试验研究[J]. 地震工程与工程振动, 2000, 20(4): 44-50.

SHI Qing-xuan, NIU Di-tao, YAN Gui-yun. Experimental research on hysteretic characteristics of corroded RC members with flexural and compressive axial loads under repeated horizontal loading[J]. Earthquake Engineering and Engineering Vibration, 2000, 20(4): 44-50. (In Chinese)

[7] MA Yin, CHI Yi, GONG Jin-xin. Behavior of corrosion damaged circular reinforced concrete columns under cyclic loading[J]. Construction and Building Materials, 2012, 29: 548-556.

[8] TUUTTI K. Corrosion of steel in concrete[R]. Stockholm: Swedish Cement and Concrete Research Institute, 1982: 469.

[9] CAIRNS J, PLIZZARI G A, DU Y G,etal. Mechanical properties of corrosion-damaged reinforcement[J]. ACI Materials Journal, 2005, 102(4): 256-264.

[10]DU Y G, CLARK L A, CHAN A H C. Residual capacity of corroded reinforcing bars[J]. Magazine of Concrete Research, 2005, 57(3): 135-147.

[11]MAZZOUNI S， MCKENNA F，SCOTT M H.Open system for earthquake engineering simulation user command language manual[R].Berkeley: Earthquake Engineering Research Center, University of California,2005:11-426.

[12]YASSIN M H M. Nonlinear analysis of prestressed concrete structures under monotonic and cycling loads[D]. Berkeley: University of California, 1994: 127-154.

[13]FILIPPOU F C, POPOV E P, BERTERO V V. Effects of bond deterioration on hysteretic behavior of reinforced concrete joints[R]. Berkeley: Earthquake Engineering Research Center, University of California, 1983: 93-112.

[14]MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, ASCE, 1988, 114(8): 1804-1826.

[15]ZHAO J, SRITHARAN S. Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures[J]. ACI Structural Journal, 2007, 104(2): 133-141.

[16] ELWOODL K J, MOEHLE J P. Dynamic shear and axial-load failure of reinforced concrete columns[J]. Journal of Structural Engineering, ASCE, 2008, 134(7): 1189-1198.

[17]司炳君, 李宏男, 王东升,等. 基于位移设计的钢筋混凝土桥墩抗震性能试验研究(I):拟静力试验[J]. 地震工程与工程振动, 2008, 28(1): 123-129.

SI Bing-jun, LI Hong-nan, WANG Dong-sheng,etal. Experimental evaluation of the seismic performance of reinforced concrete bridge piers designed on the basis of displacement(I): Quasi-static test[J]. Journal of Earthquake Engineering and Engineering Vibration, 2008, 28(1): 123-129. (In Chinese)

[18]范立础, 卓卫东. 桥梁延性抗震设计[M]. 北京: 人民交通出版社, 2001:265-290.

FAN Li-chu, ZHUO Wei-dong. Seismic design of bridge ductility[M]. Beijing: China Communications Press, 2001:265-290. (In Chinese)

[19]LOH C H, WAN S, LIAO W I. Effects of hysteretic model on seismic demands: consideration of near-fault ground motions[J]. The Structural Design of Tall Buildings, 2002, 11(3): 155-169.

[20]陈亮. 地震动的频谱变异性对桥墩地震反应的影响研究[J]. 土木工程学报, 2013,46(S2): 237-241.

CHEN Liang. Effects of the variability of response spectra of strong ground motions on seismic response of bridge columns[J]. China Civil Engineering Journal, 2013,46(S2): 237-241. (In Chinese)

[21]VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis[J]. Earthquake Engineering and Structural Dynamics, 2002, 31: 491- 514.

Incremental Dynamic Analysis of Corroded Reinforced Concrete Bridge Columns Subjected to Near-field Earthquake

CHEN Fang-jian , YI Wei-jian†

(College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China)

Using the hysteresis test results of corroded reinforced concrete columns, the accuracy of the model of corroded steel in reinforced concrete structures was validated. The feasibility of OPENSEES program for the nonlinear dynamic analysis of reinforced concrete structure was verified with the shaking-table test results of reinforced concrete frame. With the program and 30 seismic ground motions selected from the PEER database, a dynamic elastic-plastic finite element model was built. And then, the seismic performance of a corroded reinforced concrete bridge column subjected to far-field earthquake, near-field earthquake with or without impulse action was measured by the nonlinear dynamic time-history analysis in order to study the steel corrosion effect on the structural response under three types of earthquake ground motions. Aiming at the near-field earthquake with impulse action, the Incremental Dynamic Analysis (IDA) was carried out, the IDA curves and the influence of steel corrosion on the seismic performance of the bridge columns were obtained. The results show that near-field earthquake with pulse action has the most significant effect on the structural seismic performance when considering the corrosion, and special attention should be paid to that during structural seismic design.

steel corrosion; RC bridge columns; OPENSEES; near-field earthquake; Incremental Dynamic Analysis

1674-2974(2015)03-0001-08

2014-07-18

国家自然科学基金资助项目(51178175,51338004)，National Natural Science Foundation of China(51178175,51338004)

陈昉健(1986-)，男，湖南长沙人，湖南大学博士研究生

†通讯联系人，E-mail:wjyi @hnu.edu.cn

P315.9；TU375.3

A