哈尔滨市寒冷月份空气质量指数与空气污染物的相关性1)
2015-03-07张燕杰ZeyiLin郑煜
张燕杰 Zeyi Lin 郑煜
(东北林业大学,哈尔滨,150040) (University of Illinois at Urbana-Champaign) (东北林业大学)
责任编辑:张 玉。
空气质量指数(AQI)是定量描述空气质量状况的无量纲指数,是以空气中能够对人体造成危害的污染物为基础的空气质量评价体系[1]。许多学者对AQI 进行研究分析,并取得了许多重要的成果。A.Kumar et al[2-3]利用PCA 神经网络、主成分回归模型、时间序列回归模型以及二者的结合,对新德里市每日AQI 进 行 预 测。M.Ahmadi et al[4]在 对2000—2009年德黑兰市AQI、高速路发展情况以及汽车更新换代情况进行研究表明,3 者之间有直接关系。高庆先等[5]在对中美两国空气质量研究现状的对比分析中表明,虽然中国环境空气质量标准的研究、制定和发布的时间较晚,但发展迅速,标准中所包含的污染物指标更全面,更加客观的反映了中国空气污染特征。詹长根等[6]运用GIS 空间分析工具,对武汉市AQI 的空间分布特征进行了研究,同时分别建立了AQI 与PM2.5、PM10、CO、SO2、NO2、O3的一元线性回归方程,结果表明:6 项污染物均分别与AQI 呈高度相关,且PM2.5与AQI 的相关程度最大。
以上研究分析了各个空气污染物与AQI 的直接作用,但并未分析空气污染物对AQI 的间接作用。本研究建立了空气污染物与AQI 的主成分回归方程,确定了对AQI 起主要作用的空气污染物。运用通径分析方法,研究各个空气污染物与AQI 间的相互关系,分析出空气污染物对AQI 的直接作用和间接作用,从而确定了空气污染物对AQI 的总作用,弥补了一元、多元回归分析与相关性分析方法的不足。
1 研究区域概况
哈尔滨位于中国东北部,属于中温带大陆性季风气候,四季分明,冬季寒冷干燥,主要依靠燃煤供暖。根据哈尔滨市环保局公布的数据显示,2014年,哈尔滨市空气质量超标达到123 d,占全年空气质量超标总量的33.7%,其中:1—2月份哈尔滨市空气质量超标为47 d(轻度污染13 d,中度污染18 d,重度污染16 d,严重污染2 d),占2 个月总时间的79.7%。
2 研究方法
2.1 数据来源
本文选取哈尔滨市环保局在环保网(http://www.hrbh bj.gov.cn/)公布的2014年1—2月份AQI实时监测数据。每日对监测数据进行收集整理,得到了AQI 的实时值以及PM2.5、PM10、CO、SO2、NO2、O3(1h)和O3(8h)共7 项污染物的实时质量浓度。
2.2 主成分回归模型的建立与检验
主成分回归是W.F.Massy 于1965年根据主成分分析的思想提出了主成分回归[7]。主成分分析是消除多维随机变量各个分量间线性相关性以及变量系统降维的基本方法。在自变量间存在严重的多重共线性的情况下,主成分回归能消除多重共线性,并且极大地提高模型的精度和可靠性,保留了相关性显著的所有自变量。主成分回归模型的建立方法如下。
(1)对数据进行标准化处理,并计算样本数据X的相关阵R;
(2)求矩阵R 的前m 个特征值,以及m 个特征值所对应的特征向量,保留特征值大于1 对应的主成分,从而确定k 个主成分;
(3)将k 个主成分与因变量进行最小二乘回归;
(4)返回到原来的参数,得到因变量对原始自变量的主成分估计模型。
主成分回归模型的检验:
(1)回归方程的显著性检验。对于给定的水平α,当F>Fp-1,n-p(α)时,认为回归方程各个自变量与因变量有显著的线性关系。
(2)回归系数的显著性检验。对于给定的水平α,当t>tn-p(α/2)时,认为回归系数显著。
2.3 通径分析原理及方法
相关性分析与多元回归分析方法,仅可以分析出自变量对因变量的直接作用,不能分析自变量对因变量的间接作用。而通径分析是研究变量间的相互关系,将相关系数进行剖分的统计方法。它不仅可以反映自变量对因变量的直接作用,还可以反映一个自变量通过其它自变量对因变量的间接作用,从而确定出自变量对因变量的总作用,弥补了相关性分析与多元回归分析方法的不足。通径分析一般方法与步骤如下。
(1)标准化线性回归的正则方程为Rxxb*=Rxy。Rxx为x1、x2、…、xp的 相 关 阵;为xj对y 的直接影响作用,rjkb*k为xj通过xk对y 的间接影响作用;Rxy为x 对y 的相关阵。
(2)由方程Rxxb*=Rxy,得到通径系数Rxy,其中R-1xx是Rxx的逆矩阵。
(4)xj对y 的总决策系数为
3 结果与分析
3.1 相关性分析
哈尔滨市每年1—2月份最寒冷,由于供暖的原因,空气质量是1 a 中较差的月份。根据哈尔滨市2014年1—2月份AQI 实时数据及主要空气污染物质量浓度数据,对PM2.5(ρ1)、PM10(ρ2)、CO(ρ3)、SO2(ρ4)、NO2(ρ5)、O3(1h)(ρ6)、O3(8h)(ρ7)、AQI(Ⅰaq)之间的相关性及多重共线性进行分析(见表1、表2)。
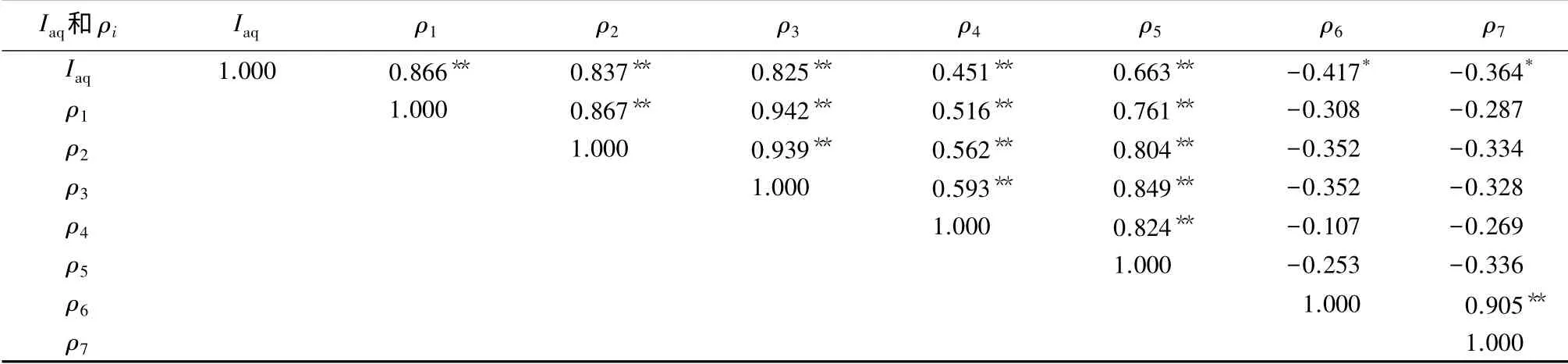
表1 相关性分析
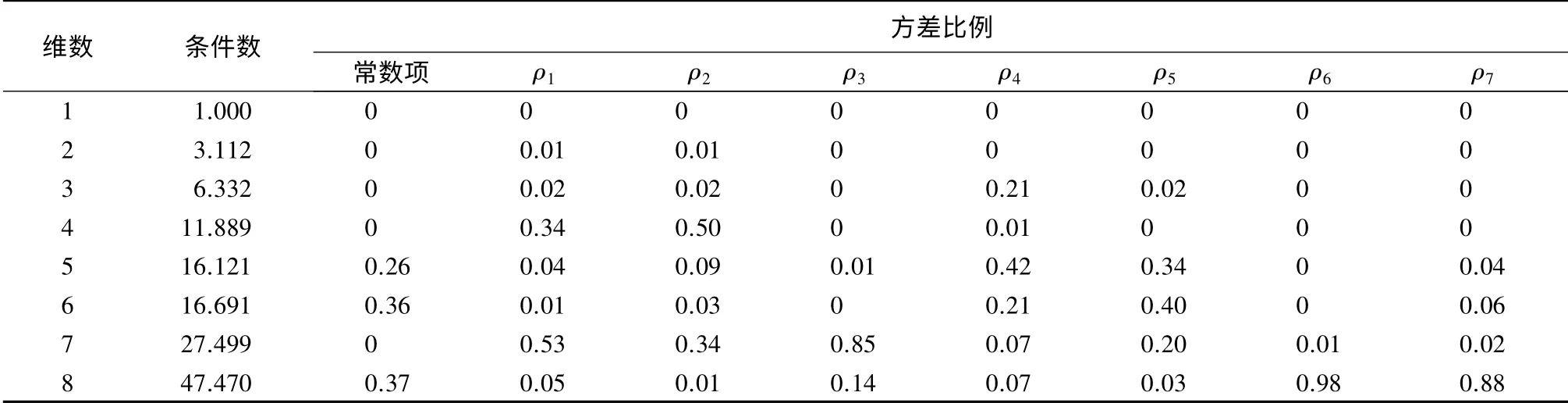
表2 多重共线性分析
由表1可见:AQI 与PM2.5、PM10、CO、SO2、NO2显著正相关,AQI 与O3(1h)、O3(8h)显著负相关;CO与PM2.5、PM10、NO2,O3(1h)与O3(8h),PM2.5与PM10,相关性极显著。由表2可见:最大条件数为47.470,远大于10,说明自变量间存在较强的多重共线性。由方差比例可知,PM2.5、PM10、CO 之间存在多重共线性,O3(1h)与O3(8h)之间存在强的多重共线性。对存在多重共线性的数据,建立多元线性回归模型将会扩大模型误差并破坏模型的稳健性;为消除自变量间的多重共线性,建立主成分回归模型。
3.2 AQI 主成分回归模型的建立与检验
以AQI(Ⅰaq)为因变量,PM2.5(ρ1)、PM10(ρ2)、CO(ρ3)、SO2(ρ4)、NO2(ρ5)、O3(1h)(ρ6)、O3(8h)(ρ7)为自变量,建立主成分回归模型(见表3~表5)。
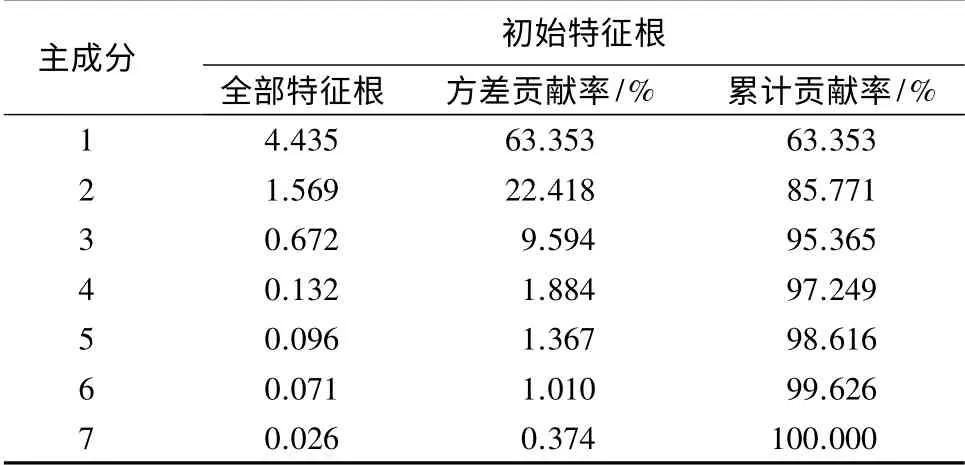
表3 方差贡献率
由表3提取出2 个特征值大于1 的主成分,其累计方差贡献率达到85.771%,包含了变量的大部分信息;因此,可以提取2 个主成分Z1、Z2,建立主成分回归建模。
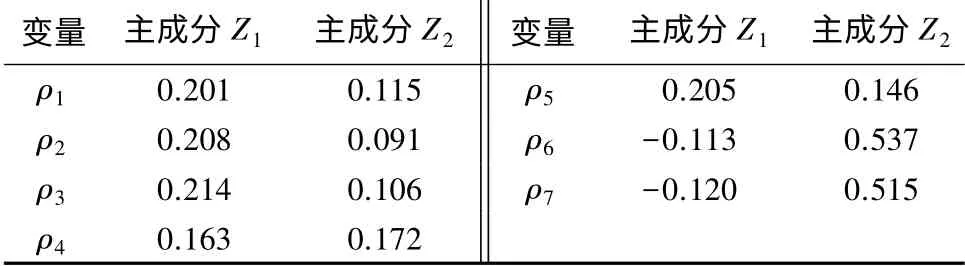
表4 主成分得分系数矩阵


表5 主成分回归模型系数
根据表5中主成分回归模型中主成分的系数,可得到标准化的主成分回归方程:
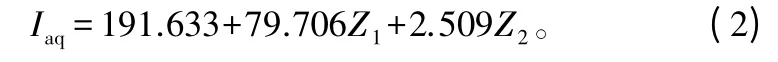
将式(1)带入到式(2)中,可得到因变量对原始自变量的主成分回归模型:
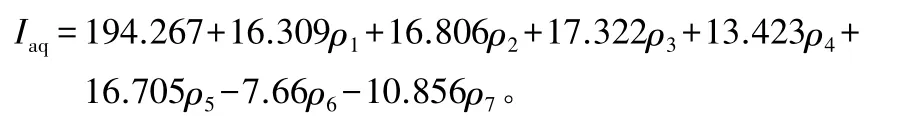
由表5可见:主成分回归系数进行显著性检验的t 值,分别为18.852、7.605、0.239,主成分回归方程系数检验显著。主成分回归模型进行显著性检验,得到F=15.138>F6,52(0.01),主成分Z1、Z2与因变量之间线性关系很显著。根据主成分回归模型可知,回归方程中系数最大的变量为CO,因此CO 对AQI 起着主要的作用。
3.3 通径分析
对因变量AQI(Ⅰaq)与自变量PM2.5(ρ1)、PM10(ρ2)、CO(ρ3)、SO2(ρ4)、NO2(ρ5)、O3(1h)(ρ6)、O3(8h)(ρ7)进行通径分析,结果见表6。
由表6可得,ρi对Ⅰaq的直接决定系数:R21=90.1%,R22=41.8%,R23=58.9%,R24=0.7%,R25=0.02%,R26=11.9%,R27=4.1%。
ρi各相关路径对Ⅰaq的决定系数:R12=56.1%,R13=-72.3%,R14=4.3%,R15=-1.1%,R16=10.7%,R17=-5.8%;R23=-72.1%,R24=4.6%,R25=-1.2%,R26=12.2%,R27=-6.7%;R34=4.9%,R35=-1.2%,R36=12.1%,R37=-6.6%;R45=-1.2%,R46=3.7%,R47=-5.4%;R56=8.7%,R57=-6.8%;R67=18.3%。“-”表示限制作用[8]。
ρi对Ⅰaq总决定系数:R2=R2i+Rik=82.8%,i、k=1、2、…、7。
剩余因素ε对Ⅰaq的直接影响作用:b*ε=
剩余因素ε对Ⅰaq的决定系数

表6 通径分析结果
通径分析结果表明:
(1)PM2.5对AQI 的直接作用最大,CO 对AQI的直接作用次之,对AQI 直接作用最小的为NO2。
(2)PM2.5通过CO 对AQI 所起到的间接作用,大于其他污染物通过CO 对AQI 的间接作用。PM10、SO2、NO2通过CO 对AQI 所起到的间接作用,均大于它们对AQI 的直接作用。
(3)对AQI 总作用最大的为PM2.5,PM10次之,总作用最小的为O3(1h)。
(4)PM2.5对AQI 的决策系数最大,PM2.5是主要决定性因素。
(5)PM2.5对AQI 的直接决定系数达到了90.1%,CO 对AQI 的直接决定系数为58.9%。
(6)剩余因素ε 对AQI 的决策系数为17.2%,表明还有其他因素对AQI 起到影响作用。
4 讨论
[6]对武汉市AQI 的空间分布特征进行了研究,得出PM2.5、PM10、CO、SO2、NO2、O3与AQI 呈高度相关,且PM2.5与AQI 的相关程度最大。本文不仅得出AQI 与PM2.5、PM10、CO、SO2、NO2呈显著正相关,AQI 与O3(1h)、O3(8h)呈显著负相关;而且分析出CO 与PM2.5相关性最显著,相关系数达到了0.942。CO 与PM10相关性次之,相关系数为0.939。PM2.5、PM10、CO 之间存在多重共线性,O3(1h)与O3(8h)之间存在强的多重共线性。
参考文献[6]分别建立了AQI 与PM2.5、PM10、CO、SO2、NO2、O3的一元线性回归方程。本文根据相关性分析结果,建立了AQI 与PM2.5、PM10、CO、SO2、NO2、O3(1h)、O3(8h)的主成分回归模型,主成分回归方程的显著性检验与系数显著性检验均通过。回归方程中系数,最大的变量是CO,表明CO 是影响AQI 的主要因素。
参考文献[2]、[3]、[6],只给出了PM2.5、PM10、CO、SO2、NO2、O3对AQI 的直接关系。本文不仅讨论了空气污染物与AQI 的直接关系,而且运用通径分析理论分析出了PM2.5对AQI 的直接作用最大,CO 对AQI 的直接作用次之;也分析出PM2.5对AQI的总作用及决策系数均最大。PM2.5、PM10、SO2、NO2通过CO 对AQI 的间接作用,均大于它们对AQI 的直接作用,CO 在对AQI 的间接作用中起到了重要的影响。7 项主要空气污染物对AQI 的总决定系数为82.8%。PM2.5的形成过程中,CO 是影响PM2.5质量浓度变化的决定性因素[9];因此,降低大气中CO的质量浓度,可以有效的控制PM2.5质量浓度,从而控制AQI 的值,改善空气质量。
哈尔滨市1—2月份寒冷干燥,主要依靠燃煤供暖,供暖过程中煤的不完全燃烧将导致空气中的CO质量浓度升高,CO 质量浓度升高是导致AQI 值的升高的原因之一。因此,提高煤炭的充分利用率,减少汽车尾气排放量及控制工业生产过程中产生的废气量,将有利于降低AQI 值,提高空气质量。
参 考 文 献
[1] 高敏,仇天雷,贾瑞志,等.北京雾霾天气生物气溶胶浓度和粒径特征[J].环境科学,2014,35(12):4415-4421.
[2] Kumar A,Goyal P.Forecasting of daily air quality index in delhi[J].Science of the Total Environment,2011,409(24):5517-5523.
[3] Kumar A,Goyal P.Forecasting of air quality index in delhi using neural network based on principal component analysis[J].Pure and Applied Geophysics,2013,170(4):711-722.
[4] Ahmadi M,Mahmoudi P.Tehran air quality index during 2000—2009[J].Asian Journal of Chemistry,2012,24(11):4871-4874.
[5] 高庆先,刘俊蓉,李文涛,等.中美空气质量指数(AQI)对比研究及启示[J].环境科学,2015,36(4):1141-1147.
[6] 詹长根,吴艺,韦淑贞,等.基于GIS 的武汉市AQI 时空分布规律研究[J].地理空间信息,2014,12(5):62-64.
[7] 郭呈全,陈希镇.主成分回归的SPSS 实现[J].统计与决策,2011(5):157-159.
[8] 袁志发,贠海燕.试验设计与分析[M].中国农业出版社,2007:220-226.
[9] 郑煜,邓兰.基于PLS1 的哈尔滨市PM2.5与空气污染物相关性分析[J].生态环境学报,2014,23(12):1953-1957.
