基于特征矢量法的MTI滤波器的优化设计

金 丹，察 豪

（海军工程大学，武汉 430033）

基于特征矢量法的MTI滤波器的优化设计

金 丹，察 豪

（海军工程大学，武汉 430033）

为满足雷达仿真系统抑制杂波、提高雷达信号的信杂比以利于运动目标检测的研究需要，分析了MTI常用的延迟线对消器，针对其存在的不足，建立了基于特征矢量法的MTI滤波器的几何描述模型，并通过仿真对比验证了基于特征矢量法的MTI滤波器的优越性和可行性。

MTI，延迟线对消器，特征矢量法，模型仿真

0 引言

MTI是指利用杂波抑制滤波器来抑制各种杂波，提高雷达信号的信杂比，以利于运动目标检测的技术。滤波器主要分为无限脉冲响应（IIR）滤波器和有限脉冲响应（FIR）滤波器［1］。IIR滤波器的优点是可用相对较少的阶数达到预期的滤波器响应，但是其相位特性是非线性的，在MTI滤波器中很少采用，而FIR滤波器具有线性相位特性，所以MTI滤波器主要采用FIR滤波器。在脉冲雷达中MTI滤波器就是利用杂波与运动目标的多普勒频率的差异，使得滤波器的频率响应在杂波谱的位置形成“凹口”，以抑制杂波，而让动目标回波通过后的损失尽量小或者没有损失。

1 数学模型的建立

常用的MTI滤波器为延迟线对消器。延迟线对消器是最早出现，也是最常用的MTI滤波器之一。根据对消次数的不同，又分为单延迟线对消器，双延迟线对消器和多延迟线对消器［2］。

1.1 单延迟线对消器

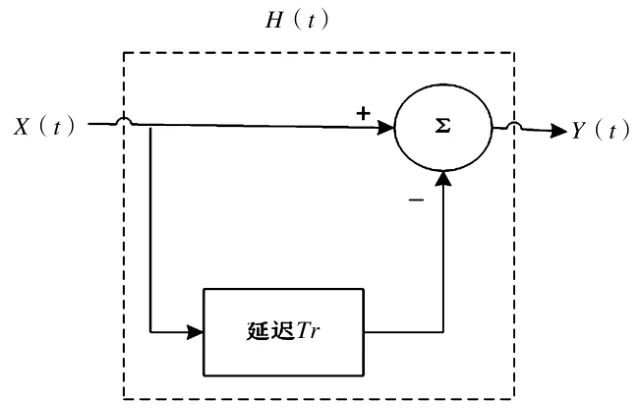
图1 单延迟线对消器

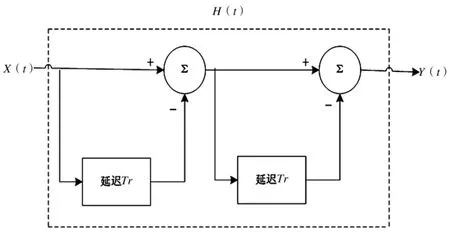
图2 双延迟线对消器

单延迟线对消器如图1所示，它由延迟时间等于发射脉冲重复周期PRI（Tr）的延迟单元（数字延迟线）和加法器组成。单延迟线对消器经常称为“两脉冲对消器”或者“一次对消器”。

对消器的脉冲响应表示为 h（t），输出 y（t），等于脉冲响应 h（t）与输入 x（t）之间的卷积。

输出信号 y（t）为

1.2 双延迟线对消器

双延迟线对消器如图2所示，它由两个单延迟线对消器级联而成。双延迟线对消器经常称为“三脉冲对消器”或者“二次对消器”。

双延迟线对消器脉冲响应为

单延迟线对消器是一个非常简单的滤波器。它的实现不需要乘法运算，每一个输出采样只需要一次减法运算。然而，与理想的高通滤波器相比，它是一个很差的近似。双延迟线对消器能够明显改善零多普勒附近的凹口宽度，但并不能改善非零多普勒频率处的频率响应。基于以上延迟线对消器的不足，提出了基于特征矢量法的MTI滤波器的优化设计。

1.3 特征矢量法

MTI滤波器的设计目标就是设计一组合适的滤波器系数，使其有效地抑制杂波，并保证目标信号能无损失地通过。特征矢量法就是一种主要的MTI滤波器的优化设计方法［3-5］

特征矢量法是以平均改善因子最大为准则的杂波抑制方法。

通常假设杂波具有高斯型功率谱，谱中心为f0，谱宽为σf，谱密度函数为：

根据维纳滤波理论，如果杂波是平稳随机过程，其功率谱与自相关函数是傅立叶变换对的关系。所以，杂波自相关函数rc（m，n）为其功率谱C（f）的傅立叶逆变换。

式中，Ci和Si分别表示MTI滤波器输入端的杂波功率和信号功率，w为FIR滤波器权系数矢量。根据MTI滤波器的改善因子的定义

在Rc的特征值中，大特征值所对应的特征向量张成的子空间为信号子空间，杂波的主要分量位于这个子空间；小特征值所对应的特征向量张成的子空间为噪声子空间。因为噪声子空间与信号子空间是正交的，所以最小特征值0所对应的特征向量W0被取为MTI滤波器的权系数向量，这就可以在最大程度上抑制杂波分量，使改善因子最大。

这种利用杂波自相关矩阵的特征分解，用其最小特征值所对应的特征向量设计MTI滤波器的方法称为特征矢量法。这种设计的滤波器可以得到良好的杂波抑制性能。

如果存在两种或两种以上的杂波，如地杂波和云雨杂波，两种杂波的谱中心可能分别位于频率轴上不同位置，对于多个高斯谱的混合杂波，其功率谱是它们各自功率谱之和，其自相关函数也由对应的多杂波分量之和构成。可以用特征矢量法设计具有两个凹口的滤波器，同时在两种杂波谱中心形成两个不同的凹口。

2 仿真实例与分析

单延迟线对消器和双延迟线对消器的归一化频率响应，从图3和图4中可以看出，双延迟线对消器比单延迟线对消器具有更好的响应（更深的凹口）。单延迟线对消器的频率响应较差，原因在于其阻带没有宽的凹口，而双延迟线对消器无论在阻带还是通带上都比单延迟线对消器有更好的频率响应。双延迟线对消器能够明显地改善零多普勒附近的凹口宽度，但并不能改善非零多普勒频率处的频率响应。

图5和图6中，平均重复频率为100 Hz，参差比为27:28:29，地杂波的中心频率为0 Hz，谱宽为0.64 Hz；云雨杂波的中心频率为 30 Hz，谱宽为1.4 Hz，使用特征矢量法设计的单凹口和双凹口对消滤波器，其归一化频率响应如图所示，其中a为单凹口，b为双凹口，分别用于对消地杂波和气象杂波。

通过仿真对比可以看出基于特征矢量法的MTI滤波器能够很好地实现零多普勒和非零多普勒频率处的频率响应，且具有一定宽度的凹口，能够针对杂波实现杂波的有效抑制。

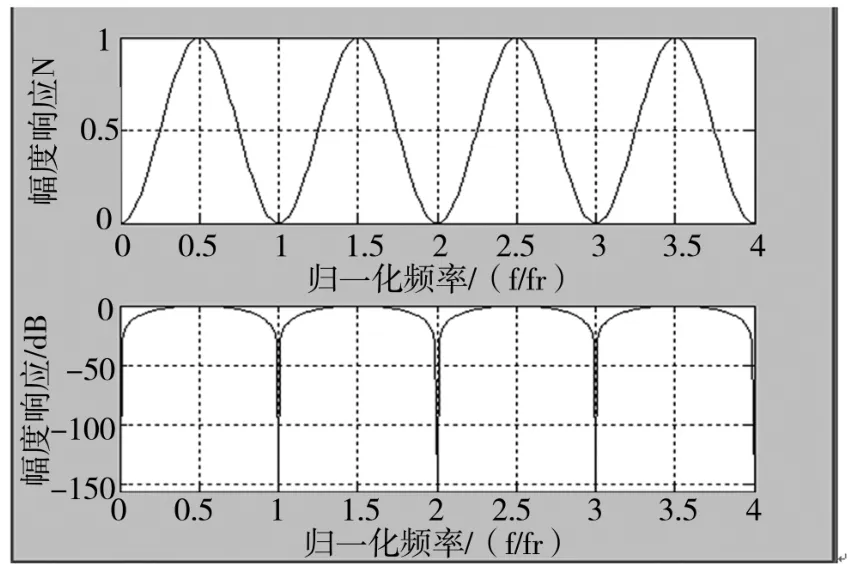
图3 单延迟线对消器归一化频率响应

图4 双延迟线对消器归一化频率响应

图5 单凹口FIR滤波器

图6 双凹口FIR滤波器

3 结论

从以上仿真可以看出，虽然延迟线对消器可以实现零多普勒处的频率响应，但由于其本身的缺点还不足以满足现实情况中的要求，而基于特征矢量法的MTI滤波器则可以很好地弥补这方面的不足，对雷达系统的仿真研究有很好的参考价值。

［1］黄莉.地基雷达的回波生成和信号处理仿真研究 [D].成都：电子科技大学，2006.

［2］邢孟道，王彤，李真芳，等.雷达信号处理基础[M].北京：电子工业出版社，2012：169-171.

［3］陈伯孝.现代雷达系统分析与设计[M].西安：西安电子科技大学出版社，2012：233-241.

［4］龙方，喻戈阳，王乃卫，等.地基雷达的MTI性能评定方法研究[J].电子对抗，2002，25（2）：39-45.

［5］张娟.雷达系统仿真、评估与实测数据分析[D].西安：西安电子科技大学，2006.

［6］朱国富，黄晓涛，黎向阳，等.雷达系统设计Matlab仿真[M].北京：电子工业出版社，2009.

Research on Optim ization ofMTIFilters Based on Eigenvector Method

JINDan，CHA Hao
（Navy University of Engineering，Wuhan 430033，China）

For the need of the clutter suppression in the simulation of radar system and the need of the improvement of the radar signal SNR to detectmoving target，it analyzeds the commonly used delay line cancellation in MTI.Aiming at the disadvantage and shortage,it establisheds a geometric model based on the eigenvector method，and through comparing the simulation，it validated the feasibility and superiority of the eigenvectormethod.

MTI，delay line cancellation，eigenvectormethod，modelsimulation

TJ630

A

1002-0640（2015）11-0120-03

2014-10-05

2014-11-07

金 丹（1968- ），女，山东烟台人，博士生。研究方向：通信与信息系统。