高阶M IMO下基于格基规约的K-best检测改进算法*

杨大江，宋常建，钟子发

（电子工程学院安徽省电子制约技术重点实验室，合肥 230037）

高阶M IMO下基于格基规约的K-best检测改进算法*

杨大江，宋常建，钟子发

（电子工程学院安徽省电子制约技术重点实验室，合肥 230037）

通过对k-best检测算法的分析，在研究了格基规约（Lattice Reduction，LR）原理的基础上，结合对基于LR的MMSE-SIC检测算法的比较，验证了对信道矩阵进行LR预处理后，信号检测性能能得到近6-dB的提升，由此，在8*8多天线系统下，提出了一种基于LR的SR-k-best检测算法，经过仿真比较发现，该算法检测复杂度更低，而降低的检测性能可以忽略不计，是一种近最优的低复杂度高阶MIMO检测算法。

高阶MIMO，格基规约，K-best，信号检测

0 引言

B3G/4G之后的移动通信系统的一个重要特征就是采用了 MIMO（Multiple InputMultiple Output）多天线技术，作为多天线系统，MIMO利用分集和复用的特性能够显著提升无线通信中的数据传输速率。理论证明，MIMO的信道容量与最小天线数目间呈近似线性增长的关系［1］。天线数目越多，信道容量越大；在相同的时间、空间和频域内传输的数据越多，频谱效率也就越高。目前对天线数目仅数根如1*2，2*2，4*2，4*4（LTE（3GPPRelease 9）支持的天线配置［2］）的常规MIMO的研究已非常成熟，而对天线数目更多的高阶MIMO（定义天线数目在8~32之间）的研究却刚刚起步，并逐渐成为当今的研究热点。文献［3］中最早提出 LR（Lattice Reduction，LR）算法用于常规MIMO信号检测；后续的研究中，基于LR算法的MMSE-SIC算法被提出［4］，仿真表明，该算法能取得近似ML检测性能。LR算法计算复杂度多项式级，随着基础向量数的增加，其复杂度相应的增长，所以，在高阶MIMO下，检测复杂度很高。文献［5］提出了一种降低高阶MIMO计算复杂度的方法，即通过SIC算法将高阶MIMO分解成多个小的MIMO检测问题，但同时，SIC会带来误差传播的不利影响，以致检测过程中不能取得稳定的检测性能。K-best球形译码算法作为一种次优的检测算法，在常规MIMO检测中能取得近ML的检测性能，且具有相对固定的检测复杂度。而格基规约对减少信道矩阵的条件数非常有用，适用于高阶MIMO的信号检测问题，在结合了K-best检测原理的基础上，本文提出一种改进算法，用于高阶MIMO下信号检测，进一步降低了检测复杂度。

1 系统模型

考虑一个Nr×Nt的MIMO系统模型，为接收信号向量

根据式（2）的模型，可以得到其最优的最大似然检测为：

2 基于LR的检测算法

2.1 LR基本原理

LR是一种预处理操作，运用到MIMO信号检测中，能改善信道矩阵的奇异性，进而达到改善MIMO信号的检测性能以及降低检测复杂度的目的。

图1 具有大条件数的基向量集

图2 正交基向量集

LR技术就是优化格的产生矩阵T，使新的产生矩阵HT更加正交，模值更小。通常高维的LR是一个NP-hard问题，为解决这个问题，学者们提出了多项式时间、次优的实数域LLL算法其只能对取值为实数的信道矩阵进行操作;对于复数信道矩阵，就需要对其进行维度扩展变为实数矩阵再进行相应的格基约减算法，而维度扩展往往会带来复杂度的增加［6］，在此基础上，在此基础上，文献［7］中提出了一种CLLL算法，能够直接对复数矩阵进行LR操作，从而避免了复数域到实数域的扩展，降低了计算复杂度。

2.2 LR在高阶MIMO检测中的应用

根据第1节中所给的MIMO系统模型，结合2.1节中LR的基本原理，下面给出LRA检测的具体流程［8］：

第1步，对接收信号矢量y进行适当的平移和伸缩，以保证等效的发送信号是复整数。

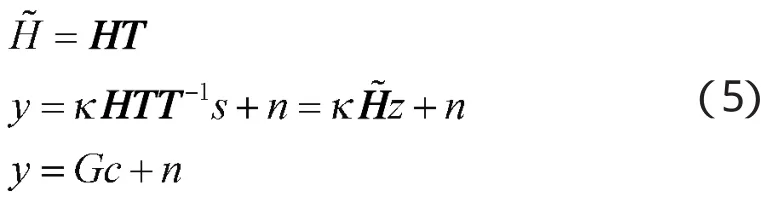
第4步，由第3步得到的z^，再通过矩阵变换得到s^，最后对s^进行线性变换得到x^。

2.3 基于LR的MMSE-SIC检测

根据第1节中所给的系统模型

然后再根据MMSE-SIC检测算法，估计出cex，令 ce，xj及 rp，q分别代表 cex的第 i个元素、x 的第 j个元素及矩阵Rex的第（p，q）个元素，取Rex的最后一行，待估向量cex的第M个符号进行检测

高阶MIMO下，随着发射、接收天线数的增长，信道之间的相关性随之增加，这里引用一种Kronecker模型来模拟LRA在高阶MIMO下检测的过程

式中，G为非相关的联合高斯系数组成的矩阵；

其中，p为信道间的相关参数（0

3 K-best球形检测算法

3.1 K-best球形算法原理及步骤

K-best球形检测算法（Sphere Decoding Algorithm，SDA）相比于传统的球形译码算法来说并不是最优的，由于其缩小了搜索的空间，故在检测性能上会有所下降，但是由于其具有了固定的检测复杂度，使其在实际应用中成为了可能，在高阶MIMO检测方面也具有了一定的优势，下面结合所给系统模型，对K-bestSDA算法的关键流程给予详细介绍。

然后，第i+1层需要对这k个子向量进行扩展，每一个节点可以扩展出M个子节点，这样，第i+1层共扩展出了M×K个子节点；

根据局部欧式距离（Partial Euclidean Distance，PED）的计算公式：

其中，Ti（x）表示PED的值，其计算初始值为0，|ei（x）|2表示第i层与i+1层之间增加的距离，K-best算法描述如下：

①初始化：在第NT+1层指定一条路径且PED=0；

②扩展：根据算法原理，扩展k条路径到M个子节点，对于每一条路径，由式（12）计算出更新的PED值；

③排序选择：在M×k各可能的过程中，对它们的PED值进行排序，并选择最好的K条路径；

④如果没有到达最后一层，则返回步骤②，否则，停止。

根据k-best算法原理及流程，其在路径选取上只是选择了最佳了K条路径，这样，就降低了一定的检测性能，选择不同的参数k对k-best检测算法性能会有不一样的影响，k值的选择依据对系统检测性能的要求而定。

4 基于LR的K-best检测的改进算法

LR操作可以改善矩阵，使得等效矩阵的奇异性得以改善；同时，LR算法具有很好的算法重构性，能与各种线性、非线性的信号检测算法相结合，上节中介绍了基于LR的MMSE-SIC检测算法，本节中，将对基与LR的K-best算法作改进，解决随着K值的上升，排序复杂度增大的问题。

4.1 基于LR的SR-K-best算法原理

根据k-best算法步骤③可知，要对M×k个子节点中排序选择最优的K个节点，文献［11］中提出的D-k-best算法，对此步骤作了改进，将复杂度降到每层的k个候选值中作k次排序；然而，这k次排序操作仍然存在较高的复杂度与较长的延迟。因此，本节所提SR-k-best（Sorting Reduced，SR）算法对此作了改进，将排序操作次数有k次进一步降到m次，下面给出具体的算法步骤

SR-k-best 1.首先排序找到第1层的K个最佳子节点（）For（l=Nt-1；l>=1；l=l-1）2.干扰相消，找到第一个子节点l+1 3.选择（K-M）个子节点，根据预置参数（q）选择出下一个（K-M）个候选的子节点4.用得到的姊妹节点置换第2步中的子节点5.For（k=1；k＜=M；k=k+1）a）在第2步的子节点中选择minPED b）存储节点l c）a）步中的minPED对应的子节点取代它的下一个姊妹节点end end

4.2 算法复杂度分析

下面就基本的K-best算法，及已有的D-K-best算法和改进的SR-K-best算法复杂度作分析对比，列出表格如表1所示。

表1 已有的D-K-best算法和改进的SR-K-BEST算法复杂度分析对比

由上表可以明显可以看出，两种不同调制方式下，SR-k-best算法在D-k-best算法的基础上，进一步降低了检测复杂度，更是远低于基本的k-best检测复杂度。

5 仿真结果与分析

5.1 仿真参数的设置

表2 仿真参数的设置

5.2 仿真结果与分析

首先，给出4*4天线配置、64-QAM符号调制下，基于LR的常规检测算法的仿真结果图，如图3所示：

图3 基于LR的常规检测算法比较

图4 两种信道相关系数下K-best与基于LR的K-best比较

由图3可以看出，相比于MMSE-SIC算法而言，基于LR的MMSE-SIC检测算法能明显提高检测性能，可见，在接收端进行检测前，对信道矩阵H进行LR操作得到的H˜，再对其SIC干扰相消处理，信噪比越大，检测性能提升越明显。

对于高阶MIMO，给出8*8天线配置、64-QAM调制下，两种不同信道相关条件下基于LR的K-best与基本K-best比较仿真结果图。

由图4可知，随着信道间相关性的增加，信号检测的难度增加，信号检测性能下降，相关系数为p=0时（即为瑞利衰落信道），随着p的增加，当p=0.6时，对于K-best检测算法来说，有大约6-dB的性能损失，而对于LR-K-best检测，仅仅只有4.2 dB左右的性能下降，仿真结果表明，基于LR的K-best检测算法更加适用于高相关的信道下的MIMO信号检测问题。

为验证本文所提算法的有效性，下面给出基于LR的SR-k-best检测算法性能仿真图，并与图2中的基于LR的k-best检测作对比，结果如图5所示：

图5 SR-k-best算法性能仿真与比较

仿真结果表明，两种不同信道状态下，基于LR的SR-k-best检测算法与K-best检测算法性能上相差不大，约有0.2 dB的性能下降，但由表1可知，本文所提算法的计算复杂度更低，这样，以很小的性能损失换取了检测复杂度上降低，是一种低复杂度的高阶MIMO信号检测算法。

6 结论

本文对基于LR的MIMO信号检测问题进行了深入研究，分析了LR的基本原理，结合k-best算法的基础上，对子节点的搜索过程加以改进，仿真表明，改进算法能进一步降低了检测的复杂度，提高了高阶MIMO下信号检测的在实际运用中的可行性，特别是本算法在处理较大K值情况下，复杂度降低更为明显。

［1］Gan Y H，Ling C，Mow W H.Complex Lattic Reduction Algorithm for Low-complexity Full Iversity MIMO Detection［J］.IEEETrans.SignalProcess，2009，57（7）：2701-2710.

［2］ 3GPP，TS 36.211 V 1.1.0.Physical Channels and Modulation［S］.Sophia：3GPP，2008.

［3］Yao H.WornellGW （2002）Lattice Reduction Aided Detectors forMIMO Communication Systems［J］.In:Proc IEEE Globecom，2002:424-428.

［4］Debbah M，Muquet B，Courville M，etal.MMSE Successive Interference Cancellation Scheme for New Spread OFDM Systems［J］.IEEE（VTC）Springapan，2000（5）：745-749.

［5］Kumar A，Chandrasekaran S，Chockalingam A，etal.Near-Optimal Large-MIMO Detection Using Randomized MCMC and Randomized Search Algorithms，in Proc［C］//IEEE International Conference on Communications（ICC），Kyoto，Japan，2011：22-25.

［6］赵慧，龙航，王文博.降低高条件数信道下的球形译码算法复杂度的方法［J］.电子与信息学报，2009，31（3）：636-639.

［7］Choi J，Nguyen H.SIC-based Detectionwith Listand Lattice Reduction forMIMOChannels［J］.IEEE Trans.Veh.Technol，2009，58（7）:3786-3790.

［8］Agrell E，Eriksson T，Vardy A，etal.Closest Point Search in Lattices［J］.IEEE Transactions.Inf.Theory，2002（48）:2201-2214.

［9］ Kumar S.Chandrasekaran，Chockalingam A，et al.Rajan，Near-Optimal Large-MIMO Detection Using Randomized MCMC and Randomized Search Algorithms［C］//in Proc.IEEE International Conference on Communications（ICC），Kyoto，Japan，Jun.2011.

［10］Chang H C，Liao Y C，Chang H C.Low-complexity Prediction Techniques of K-best Sphere Decoding for MIMO Systems［J］.IEEEWork-shop，2007（10）:45-49.

［11］ Liu L，Lofgren J，Nilsson P.Area-efficient Configurable High Throughput Signal Detector Supporting Multiple MIMOModes［J］.IEEE Traps.Circuits Syst.IReg.Papers，2012，59（9）：2085-2096.

Under Statuteof Higher-Order M IMO Lattice-Based K-Best Detection Improved Algorithm

YANGDa-jiang，SONGChang-jian，ZHONG Zi-fa
（Electronic Engineering Institute.Key Laboratory of Electronic Restriction of Anhui Province，Hefei 230037，China）

By k-best detection algorithm analysis，studied the lattice reduction in basis（Lattice Reduction，LR）principle，combined with comparison to the MMSE-SIC detection algorithm based on the LR verified after pretreatment LR channelmatrix，the signal detection performance can be nearly 6-dB increased，whereby in the 8*8 multi-antenna system proposed SR-k-best detection algorithm based on LR.Through simulation comparison，the complexity of the detection algorithm lower detection performance decrease is negligible，which is a low-complexity near-optimal order MIMO detection algorithm.

high MIMO，lattice reduction，K-best，signaldetection

TN911.23

A

1002-0640（2015）11-0020-05

2014-09-25

2014-11-07

国家自然科学基金（11375263）；国防预研基金资助项目（41101040402）

杨大江（1989- ），男，湖南常德人，硕士研究生。研究方向：M IMO信号检测。