基于NGA算法的舰载机机库出库调度优化*

司维超，齐玉东，韩 维

（海军航空工程学院，山东 烟台 264001）

基于NGA算法的舰载机机库出库调度优化*

司维超，齐玉东，韩 维

（海军航空工程学院，山东 烟台 264001）

为了在复杂的机库环境中，尽可能缩短舰载机出库时间，优化其出库顺序，对舰载机多机出库调度优化问题进行了研究。首先，对该问题进行分析，建立了适合优化的数学模型。其次，设计了一种适合优化舰载机多机出库调度问题的算法—NGA算法，该算法是在遗传算法（GA）的基础上，对原有交叉和变异策略进行改变以适应所求解问题，并融入执行路径探测和规划的通视图算法后形成的。最后，分别将该方法和枚举法应用于求解尼米兹级航母舰载机多机出库调度优化问题T4。仿真结果为基于NGA算法所得的最短出库时间为801 s，最短移动距离为1 098.3m;基于枚举法结果为800.4 s和1 097.6m。由结果可知，NGA算法计算结果与枚举法相差较小，可以应用于求解舰载机多机出库调度问题。

舰载机，出库调度优化，改进遗传算法，枚举法，尼米兹航母

航母在目前乃至将来都是各军事强国海军的重要力量，对其搭载的舰载机进行合理保障具有重要的意义［1］。为了完成特定任务，需要从机库往舰面调运多架飞机，其中涉及飞机出库问题［2-3］。不同飞机所要调往舰面目的停机位各不同；飞机不同出库顺序，对应的出库时间和总的移动距离是不同的。为了尽量缩短出库时间和移动距离，这需在综合考虑飞机调往舰面目的停机位等基础上，对飞机的出库顺序进行优化。

当需要出库的飞机数量较多时，出库问题的解空间将会很大，使该问题成为一个NP完全问题［4］。例如，在不考虑相关约束前提下，出库12架飞机，其总共的出库顺序方案有479 001 600种。如何从众多的出库方案中，排除不可行方案，并寻找最优方案则需要进一步研究。

国外以往对于飞机的出库调度一般是通过人为进行的［5］，即调度人员根据当前机库飞机的布放情况，在满足安全的前提下，对需要出库的飞机进行排序，排序的原则一般是离升降机近的优先出库［6］。其优点是操作比较简单，适用于出库少数飞机；缺点是没有综合考虑各架飞机所要调往的舰面停机位距离远近，以及本次出库调度任务整体出动时间和移动距离优化问题，在出库飞机数量较多时，可能得出的调度结果并不是最优。国内对舰载机出库调度问题研究相对较少，主要集中在舰载机的保障方面，如文献［7］侧重于舰载机综合保障建模方法研究。

为此本文通过对飞机多机出库调度问题进行建模，并利用融合通视图算法［8］的改进遗传算法NGA对该问题进行解决，从数学方面给以依据，一定程度上解决了人工排序的缺陷。

1 多机出库调度问题数学建模

问题描述如下：

①约束条件：飞机在机库内按照一定方式进行排列，且不同飞机所要调往的舰面停机位互不相同，在进行出库方案优化时必须进行考虑；飞机在出库过程中，必须保证有可行路径，即避免与其他飞机或机库本身发生碰撞冲突，确保安全；机库空间相对有限，对使用同一升降机出库的飞机而言，每次允许1架飞机执行机库内部移动，且后移动的飞机必须等紧前飞机移动到升降机后才开始移动；升降机需根据承载能力规定一次可以升降的飞机数量；各个升降机的使用原则上是互不冲突，可独立进行，为此本章重点考虑使用一个升降机时的多机出库优化问题。

②多目标：已知待出库多架飞机所处机库停机位及其所要调往的舰面目的停机位，则不同的出库顺序所对应的出库任务总的出库时间和总的移动距离互有差异，为此可以选择在优先保证出库时间最短基础上，尽量保证移动距离也最短作为待优化的目标。

③优化内容：在满足上述约束条件的前提下，对使用同一个升降机执行出库操作的多架飞机进行合理的排序，给出最优出库方案，使得在优先保证飞机总的出库时间最短的基础上，也尽可能缩短其总的移动距离。

针对某一具体的出动任务，令需要出库飞机数量为n；所使用的升降机序号为μ。则建立数学模型如下所示。

目标函数:

其中，F为所要达到的目标函数，即在优先保证n架飞机总的出库时间最短的基础上，也尽可能缩短其总的移动距离。Xi为第i种飞机出库方案，主要由n架飞机按照出库顺序对其所处机库停机位编号进行排序组成，用作目标函数F的输入参数。S代表总的移动距离计算函数，参数为n架飞机所处机库停机位的某种排序方案Xi。S需要在满足约束条件下，根据不同航母的不同出库方案动态给出。T代表总的出动时间计算函数，参数为n架飞机所处机库停机位的某种排序方案Xi。T需要在满足约束条件下，根据不同航母的不同出库任务动态给出。

约束条件

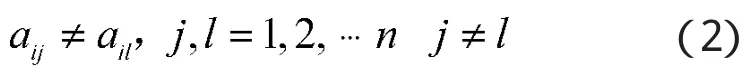
其中，aij为第i种出库方案中的第j架顺序出库的飞机所处停机位编号。式（2）表示各架飞机必须按照顺序无重复出动。

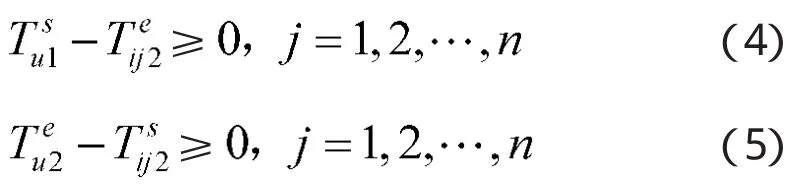
2 基于NGA算法的多机出库优化

2.1 NGA算法设计

常规单一的遗传算法对飞机出库方案优化问题，并不能完全适应，必须对其进行相应的转变，为此本节通过对交叉和变异策略进行改变，并融入执行路径探测和规划的通视图算法，形成了适用于优化飞机出库问题的NGA算法。

①融合通视图法的NGA算法操作流程如图1所示。

图1 MGA算法基本流程图

②基于NGA算法优化的基本思路

在利用NGA算法求解多机出库调度方案过程中，飞机总的出库时间以及总的移动距离可以作为算法的适应度函数；某种出库方案可以作为NGA算法的某条染色体。通过不断进化染色体，并进行通视图法可行路径探测及规划，也即更新了飞机出库方案，最终可以得出使得总的出动时间以及总的移动距离综合最优的某种出库方案。

2.2 基于NGA算法搜索最优出库方案的方法

①建立机库环境模型，明确多机出库环境，包括待出库飞机在机库中的布放及编号等。

②明确出库任务，确定需要出库的飞机范围。

③执行基于NGA算法的最优出库方案搜索。具体如下：

a.NGA算法基本参数的选取

采用如下参数设置：种群大小设置为300；交叉率设置为0.8［9］；最大进化代数设置为200次。

b.染色体编码动态设置

此处采用实值编码方式，即每条染色体代表一种多机的出库方案，其中的第i个基因表示该出库方案中第i顺序出库的飞机，用其所占用的机库停机位编号表示。而对于染色体的长度也必须能够根据不同任务所需出库飞机数量的不同而动态变化。

c.适应度函数的动态设置

在进化过程中，需要评价每条染色体，而评价的标准为该染色体所对应出库方案是否令目标更优，为此可选用式（1）作为适应度函数。其中总的出库时间包括所有待出库飞机机库操作时间和舰面操作（移至目的停机位等）时间之和；总的移动距离函数包括所有待出库飞机机库移动距离和舰面移动距离之和。其中所涉及到的待出库飞机的机库移动路径和时间由通视图法法计算给出；而舰面移动距离和时间可由路径规划方法计算给出［10-11］。

d.种群初始化

为缩短计算时间，此处将种群中每一条染色体均初始化为可行染色体，即均满足飞机出库相关约束条件。可行性判定为：确保该出库方案中，在除去前面已出库的（i-1）架飞机后新的机库环境中，第i架待出库飞机与升降机之间均存在可行路径。

e.执行选择算子运算

选择算子用来对群体中的个体进行优胜劣汰操作。此处采用轮盘赌选择法对种群进行选择。具体步骤如下：首先，生成选择概率CP。设群体中共有n个染色体，第i个染色体的适应度值（优先考虑总的出库时间）为fi，则该染色体的选择概率为：

其中，CPi为第i个染色体的选择概率为种群中的最大适应度值；fi为第i个染色体的适应度值表示第i个染色体参与选择的并被选中的机会值，由于此处是以总的出库时间越短越好，所以fi越小，对应越大，则其被选中的机会就越大。

其次，根据选择概率，用轮盘赌选择方法决定被选择保留到下一代的染色体。

f.执行改进交叉算子运算

此处随机取新生代中两组染色体配成一对，执行两点交叉操作。但是对配对染色体（即两种飞机出库方案）执行简单的两点交叉可能会使所生成的子个体出现元素重复的现象，而这与实际出库要求（同一机库停机位的飞机只能出库一次）相矛盾，为此需要采用某种新的交叉策略。本节采用如下策略来克服元素重复的问题，如图2所示。

图2 两点交叉更新操作示意图

●确定任意两个交叉位置a和b。

●建立两个中间个体temp1和temp2。其组成方式为：将父个体由交叉位置b至其结束的部分提前至该父个体的前端。

●分别针对两个父个体进行交叉操作。例如针对父个体1来说，首先保留交叉位置a和b之间的部分；其次，从交叉位置b开始依次顺序选择temp2的每一个基因执行插入（注意若temp2当前基因与父个体1保留部分中的基因有重复，则抛弃temp2当前基因，选择其下一个基因），直至到达父个体1染色体末端；最后，返回父个体1最前端，继续选择temp2中基因执行插入，直至到达交叉位置a为止。

g.依次遍历交叉形成的新染色体，并执行以下操作：

●对当前染色体的各个基因执行基于通视图法的可行路径探测及规划。依次遍历交叉后染色体的各个基因，判断按照当前顺序出库该基因所代表的飞机是否存在可行路径：若存在，则进一步规划路径；若不存在，则执行变异策略。

其中，通视图法的基本思路为：首先，建立障碍物凸壳环境模型，即将需要移动的飞机简化为一点，而将其他障碍物的凸多边形进行扩充，建立障碍物多边形的缓冲区［12］（障碍物多边形缓冲区是沿该多边形边界线外侧距离不超过缓冲距的点组成的区域）；其次，利用两点法建立起点和终点的连线，如果该连线不与任何障碍物凸壳模型相交，则其即为待规划的最优路径；否则，连线直接或间接穿过某障碍物凸壳模型集合，则该连线将集合中各障碍物凸壳模型分为上下两部分，此时可以将路径规划问题转换为利用凸包法求解障碍物上下两部分顶点集的凸包问题，然后通过对凸包所形成的初始路径进行优化便可以得到上下两条可行路径。其次，对当前规划出路径上相邻两个节点间的路径段重复执行以上操作，直至所有路径段均不与障碍物发生碰撞。最后，按照所记录的无碰撞路径节点建立可行路径有向图，并给出最优路径。

●根据当前基因可行性，选择性执行改进变异算子运算。

经过交叉后形成的新染色体，虽然避免了基因重复，但并不一定是可行的，为此需要对每条染色体中不可行基因执行某种变异策略。

原始变异算子在需要执行变异操作染色体中随机取该个体的某两个基因进行互换，以完成变异操作。而本节对于代表飞机出库顺序的特殊染色体，并不能随机进行基因互换，因为这样可能导致可行基因变为不可行；不可行基因仍然不可行情况的出现。为此，此处采用了一种新的变异策略，具体为：记录当前不可行基因，并判定当前所有可用基因的集合，将该不可行基因与当前可用基因集合中随机一个执行互换，并再次利用通视图法规划可行出库路径。

●根据该基因所代表飞机所要调往的舰面停机位，对其舰面移动路径进行规划，详见文献［13］。

h.在所有染色体均执行完第g.步操作之后，则计算各条新染色体的适应度值，然后返回第d.步操作，进行新一轮迭代。

i.确定算法终止条件。

通过设定进化迭代次数来终止算法。

步骤d.在步骤c.经过一定迭代次数后，染色体逐渐趋于稳定，而对应基因序列便为所要求解的最优飞机出库方案。

3 实例仿真

本节以尼米兹级航母为初始环境，对本文方法进行了仿真应用。

3.1 基础模型的建立

3.1.1 机库出库环境模型的建立

利用矩形区域表示尼米兹航母机库，如图3所示。

图3 任务T4局部机库模型

其中，坐标原点设在矩形区域的左上角，向右为X轴正方向，向下为Y轴正方向。按照比例进行缩放，设定机库大小为1 000×158 pix（pix为像素）。不同类型的飞机用不同的实体模型进行表示。各飞机布放参数如表1所示。

表1 T4飞机机库布放参数

另外，各架飞机所要调往舰面（1 597×369 pix）的停机位也互不相同，如图4所示。

图4 机库各飞机调往目的地分布图

其中，机库中1号飞机调往舰面1号位置；2号飞机调往舰面2号位置；依此类推。各舰面目的停机位坐标如表2所示。

表2 各飞机调运目的地参数

3.1.2 出库任务T4的建立

任务T4要求如图所示局部机库环境中的12架飞机，使用1号升降机执行出库操作（一次出库2架），并分别调往各自预定舰面停机位。目标是给出某种最优出库方案，使得在优先保证12架飞机出库时间最短的基础上，也尽可能缩短其总的移动距离。

3.2 NGA算法相关具体设置

3.2.1 染色体长度设置

染色体的长度应该与需要出库的飞机数量相等。任务T4需要出库12架飞机，所以染色体长度应为12。即

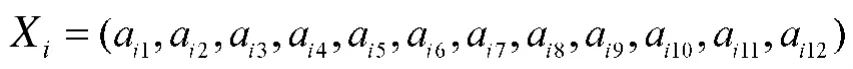
其中，Xi代表第i条染色体，也即为第i种飞机出库方案。每一维aij代表第条i染色体的第j个基因，用第j架顺序出库的飞机所处的机库停机位编号予以表示。

3.2.2 适应度函数的动态设置

3.2.2.1 飞机总的出库时间计算公式

此处飞机总的出库时间指从第1架飞机开始执行出库操作，直到最后一架飞机移动到舰面指定位置为止的整个时间。

尼米兹航母飞机出库一般流程为（以两架飞机A和B出库过程为例）：

①飞机A由机库停机位移至升降机入口位置；

②飞机A进一步移至升降机，并进行系留等操作；

③飞机B由机库停机位移至升降机入口位置；

④飞机B进一步移至升降机，并进行系留等操作；

⑤升降机将A和B升至舰面；与此同时，下一架飞机开始执行①操作；

⑥飞机A和B执行解除系留等操作，由升降机移至各自舰面目的停机位；

⑦升降机降回机库，准备接收下两架飞机。

为此，以出库1架飞机时的出库时间为基础，即

则可以给出当出库不同情况时的出库时间计算公式如下：

●当出库奇数k（k≥3）架飞机的出库时间计算公式：

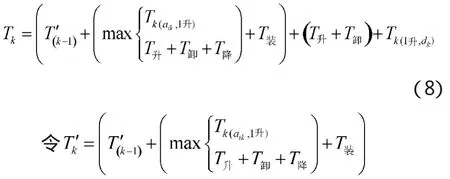
●当出库偶数l（l≥2）架飞机的出库时间计算公式：

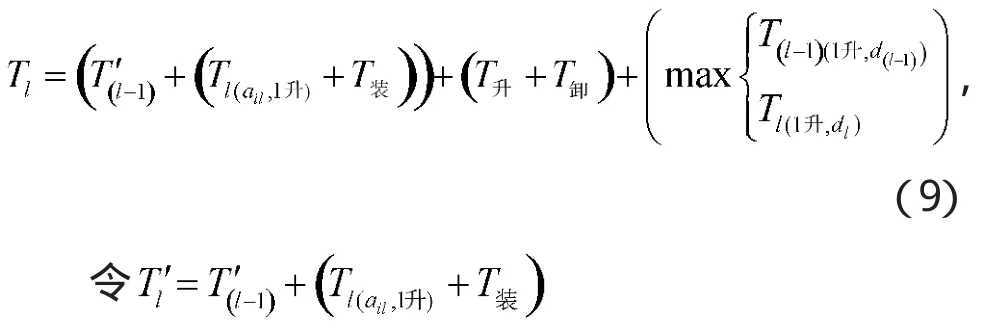
其中，各参数定义如表3所示。

表3 符号定义

3.2.2.2 飞机总的移动距离计算公式

每一架飞机的移动距离包括两部分：一是飞机在机库中的移动距离；二是飞机由升降机移至目的地的距离。而总的移动距离为所有飞机移动距离之和。

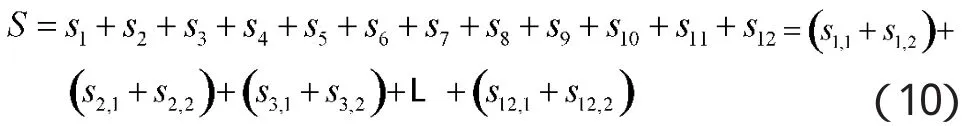
其中，si表示某种出库方案中第i架顺序出库的飞机总的移动距离，包括：由其所处的停机位移至1号升降机入口的距离si，1；由1号升降机移至舰面目的地的距离 si，2。

3.3 实例分析

3.3.1 基于NGA算法的问题求解

利用NGA算法对该问题进行求解，结果如表4所示。

表4 基于NGA的最短出动时间和移动距离

3.3.2 基于枚举法的问题求解

为了验证本章方法的有效性，此处另外采用枚举法对同一出库任务T4进行求解，给出全局最优精确解。所得结果如表5所示。

表5 枚举法计算结果

3.3.3 计算结果比较

3.3.3.1 所得出库方案结果比较

由表4和表5可以看出，基于本章方法所得的出库时间与基于枚举法的全局精确出库时间差为|801-800.4|=0.6 s；移动距离之差|1 098.3-1 097.6|=0.7m。另外，枚举法单次计算的时间为约20 h，而NGA方法仅用约90 s。

由此可知，基于本文方法所得方案与全局精确值误差较小，基本可以忽略不计，且计算时间较短，这表明本章方法在求解尼米兹级航母飞机机库出库调度问题时具有较好的有效性和快速性。

3.3.3.2 出库示例分析

此处以NGA算法所得出的全局近似最优出库方案（1；2；5；4；10；12；9；3；8；7；11；6）为例进行说明：

●优先出库阻碍其他飞机正常使用升降机的飞机，即1、2号飞机。

●出库5号飞机。在1、2号飞机已经出库前提下，5号飞机与升降机之间存在可行路径。

●出库4号飞机。在1、2号飞机已经出库前提下，4号飞机与升降机之间存在可行路径。

●出库10号飞机。在1、2、5号飞机已经出库前提下，10号飞机与升降机之间存在可行路径。

●出库12号飞机。在2、4号飞机已经出库前提下，12号飞机与升降机之间存在可行路径。

●出库9号飞机。在1、2、5、10号飞机已经出库前提下，9号飞机与升降机之间存在可行路径。

●出库3号飞机。在2号飞机已经出库前提下，3号飞机与升降机之间存在可行路径。

●出库 8号飞机。在 1、2、5、9、10号飞机已经出库前提下，8号飞机与升降机之间存在可行路径。

●出库 7号飞机。在 1、2、5、8、9、10号飞机已经出库前提下，7号飞机与升降机之间存在可行路径。

●出库11号飞机。在1、2、4号飞机已经出库前提下，11号飞机与升降机之间存在可行路径。

●最后出库6号飞机。

该方案综合考虑了各架飞机所处机库停机位及其所要调往的舰面停机位，在确保了每架飞机出库时具有可行路径的基础上，给出的飞机最优出库顺序，与实际要求相符。这表明基于本文方法在求解尼米兹级航母飞机机库出库调度问题时具有较好可行性。

4 结论

本文针对舰载机多机出库问题进行了优化研究。分析了舰载机出库调度问题，并建立了需要优化的数学模型；为了解决该问题，在分析GA算法的基础上，通过对交叉和变异策略进行改变，并融入执行路径探测和规划的通视图算法，形成了适用于优化舰载机出库问题的NGA算法；将NGA算法在尼米兹航母的舰载机多机出库问题上进行仿真应用，结果表明该方法无论在结果的准确性，还是在计算时间上的快速性等都满足实际要求。

［1］谭晓寅，徐忠平，郑文祥.现代战争武器揭秘—航母［M］.上海：百家出版社，2008.

［2］韩维，王庆官.航母与飞机概论［M］.烟台:海军航空工程学院出版，2009：10-120.

［3］ Jeffrey S.Feasibility Study of Global-Positioning-System-Based Aircraft-Carrier Flight-Deck Persistent Monitoring System［C］//JOURNAL OF AIRCRAFT，2010，47（5）.

［4］孙诗南.现代航空母舰［M］.上海:科学普及出版社，2000:1-100.

［5］ Jeffrey S J.A Feasibility Study of a Persistent Monitoring System for the Flight Deck of U.S.Navy Aircraft Carriers［D］.DEPARTMENTOF THE AIR FORCE AIR UNIVERSITY，2009.

［6］ Authority of the Chief of Naval Operations.NAVAIR 00-80T-120.CV Flight/Hangar Deck NATOPS Manual［R］.WASHINGTON，D.C.，2001.

［7］冯强，曾生奎，康锐.基于多主体的舰载机综合保障过程建模方法 ［J］.系统工程与电子技术，2010，32（1）：211-216.

［8］ Asano T，Guibas L，Hershberger J，et al.Visibility-polygon Search and Euclidean ShortestPath［C］//Berkeley，CA:The Proceedingsof26th Symposium on FoundationsofComputer Science，1989:155-164.

［9］王小平，曹立明.遗传算法理论、应用与软件实现［M］.西安:西安交通大学出版社，2002:1-50，124-141.

［10］Dieguez A R，Sanz R，Lopez J.Deliberative on-line Local Path Planning for Autonomous Mobile Robots［J］.Journal of Intelligentand Robotic Systems，2003，37（1）：1219.

［11］郑昌文，严平，丁明跃，等.飞行器航迹规划［M］.北京：国防工业出版社，2008：70-79.

［12］杨毅，刘亚辰.一种基于凸壳的智能服务机器人路径规划算法［J］.北京理工大学学报，2011，31（1）：54-58.

［13］韩维，司维超，丁大春，等.基于聚类PSO算法的飞机舰面多路径动态规划［J］.北京航空航天大学学报，2013，39（5）：610-614.

Hangar-exporting Optim ization ScheduleofM ulti-carrier Plane Based on NGA

SIWei-chao，QIYu-dong，HANWei
（Naval Aeronautical and Astronautical university，Yantai264001，China）

In order to reduce carrier plane hangar-exporting time and optimize sequence in complicated hangar environment，it researched the carrier plane hangar-exporting optimization problem.Firstly，the mathematic model of carrier plane hangar-exporting optimization problem is established.Secondly，it designed NGA algorithm which is suitable for solving the problem.NGA changed original crossover and variation tactics of GA in order to suit hangar-exporting problem，and combined Visibility Graph Algorithm which is used to detect and plan route.Finally，it used NGA and enumeration to solve the carrier plane hangar-exporting optimization problem （T4） in hangar of Nimetz aircraft carrier separately.Results are that the shortest hangar-exporting time is 801 s and shortest distance is 1098.3m based on NGA;based on enumeration it is 800.4 s and 1 097.6 m.From the results，we can know that the difference of results based on NGA and enumeration is small，and it is suitable for using NGA to solve the carrier plane hangar-exporting optimization problem.

carrier plane，hangar-exporting optimization，NGA，enumeration method，nimetz aircraft carrier

TP202；E9

A

1002-0640（2015）11-0013-07

2014-10-25

2014-11-12

军队“十二五”预先研究基金资助项目

司维超（1984- ），男，山东淄博人，博士，讲师。研究方向：指挥控制。