基于剪应力模型的履带车辆转向力矩分析与试验
2015-02-28芮强王红岩王钦龙郭静邹天刚万丽
芮强,王红岩,王钦龙,郭静,邹天刚,万丽
(1. 装甲兵工程学院 机械工程系,北京100072;2. 中国北方车辆研究所 车辆传动重点实验室,北京100072;3. 中国北方特种车辆研究所,北京100072)
0 引言
转向性能的好坏是影响高速履带车辆越野机动性的重要方面,随着高速履带车辆机动性的日益提高,对履带车辆的转向性能也提出了更高的要求。建立准确的转向动力学模型是分析研究履带车辆转向运动学、动力学性能的重要技术手段。然而,由于履带车辆转向过程始终伴随着两侧履带滑转与滑移现象的存在,使得不考虑履带滑转、滑移转向模型的计算结果与试验结果存在着很大的差异。
为了提高履带车辆转向模型的模拟精度,考虑履带打滑条件的转向理论已成为研究履带车辆转向问题中应用最为广泛的技术方法。近几年来,研究人员对履带车辆的转向机理进行了深入研究[1-4]。文献[1,5]中提到,Steeds 等假设履带-地面之间的剪切应力与剪切位移服从库仑摩擦准则,建立了考虑打滑条件下的履带车辆转向模型,其研究工作为履带车辆转向理论研究奠定了基础。然而,由于Steeds 模型采用了库仑摩擦假设,计算得到的两侧履带牵引力、制动力以及转向阻力矩等不随车辆转向半径的变化而变化,这与履带车辆实车测试的试验结果相矛盾[5-7]。为此,Said 等[4]、Wong 等[8]采用剪切应力-剪切位移关系模型来模拟履带-地面之间的切向力,通过详细的运动学、动力学分析,研究了履带车辆两侧履带的牵引力、制动力、主动轮转矩以及转向阻力矩等随转向半径的变化规律。与Steeds 模型相比,Wong 模型[8]的计算结果与Ehlert等[5]的试验结果具有很好的一致性。
本文基于剪切应力-剪切位移关系模型计算履带-地面之间的切向力,通过引入转向极横向偏移量A1、A2和转向极纵向偏移量s0,推导了考虑履带滑转、滑移以及离心力影响的履带车辆转向运动方程,构建了履带车辆稳态转向模型。采用数值迭代的方法计算履带车辆的转向运动学及动力学特性,基于实车试验数据对转向模型进行验证,并分析离心力对转向性能的影响,研究结果可以为新型转向机构的设计和转向过程控制研究提供理论支持。
1 履带车辆转向运动学模型
1.1 基本假设及坐标系
1.1.1 假设条件
根据研究问题需要作如下假设:
1)履带车辆在水平地面上作均匀稳态转向运动,车辆处于静止状态时,两侧履带接地压力为均匀分布。
2)地面为硬路或铺装路,不计履带的沉陷以及履带板在侧向方向的推土效应。
3)履带为不可拉伸的均匀柔性带,不计履带宽度影响,不考虑履带张力的变化对接地压力的影响。
4)转向过程中车辆的行驶阻力系数与直线行驶时相同。
5)转向过程中,履带上任意一点的剪切应力与该点的剪切位移量相关,其表达式为τ = τmax(1 -e-j/K),其中τmax为履带与地面之间的最大剪切应力,j 为土壤的剪切位移量,K 为土壤抗剪模量,且剪切应力方向与该点的滑动速度方向相反。
1.1.2 坐标系描述
为分析履带车辆在水平地面上的转向运动学特性,假定车体在转向过程中作3 自由度平面运动,图1为履带车辆转向运动学简图。在水平地面上建立惯性坐标系OXY,并以履带车辆转向中心线与车体纵向中心线的交点o 为坐标原点建立固结于车体上的连体坐标系oxy.
图1中:OS点为履带车辆稳态转向时的转向中心;O2'、O1' 点分别为高速侧和低速侧履带接地段的瞬时转向中心;R 为车辆的转向半径;R'为转向中心OS到车辆质心G 的横向距离,满足s0为车辆质心G 到通过O'2、O'1点连线的纵向距离,即转向极纵向偏移量;cx、cy分别为车辆质心G 到车辆几何中心的横向及纵向距离;车辆稳态转向角速度用来表示;L、B、b 分别为履带接地长、两侧履带中心距以及履带板宽度;β 为履带车辆侧滑角,β =arcsin(s0/R);P2(x2,y2)、P1(x1,y1)分别为高速侧和低速侧履带纵向中心线上取的任意一点;vs2、vs1分别为P2点和P1点的滑动速度;vsx2、vsx1分别为P2点和P1点的横向滑动速度;vsy2、vsy1分别为P2点和P1点的纵向滑动速度;dF2、dF1分别为P2点和P1点单位面积上受到的切向力。为便于描述,文中以下标1 对应内侧履带,下标2 对应外侧履带。
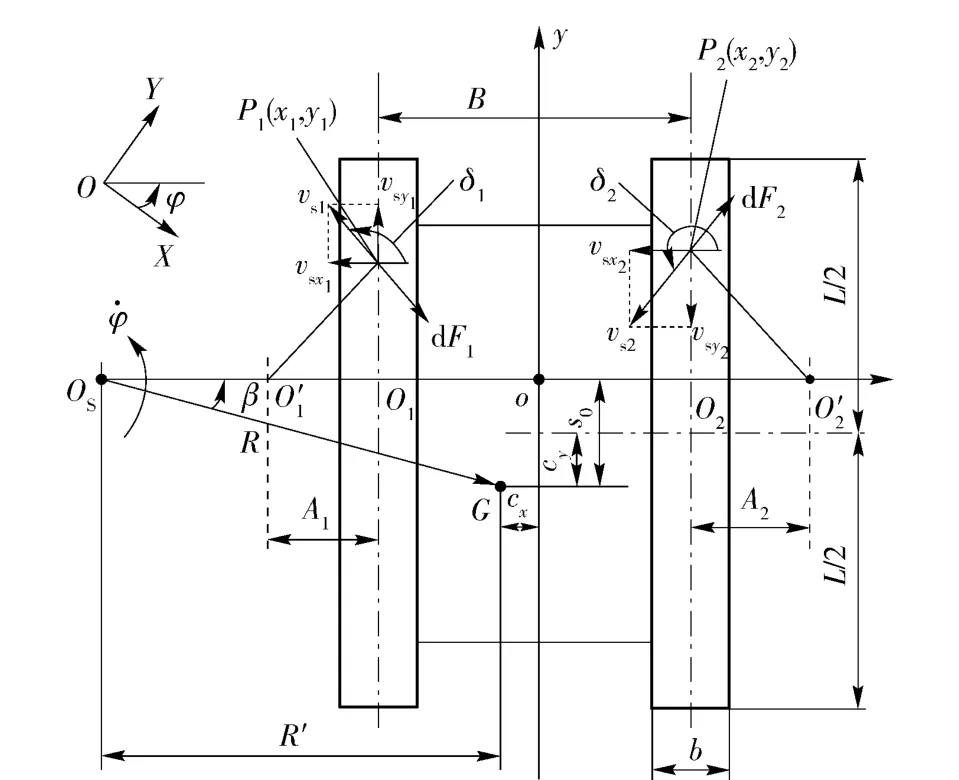
图1 稳态转向时坐标系及运动关系简图Fig. 1 Coordinate system and kinematics schematic for steady-state steering process of tracked vehicle
如图1中所示,车体连体坐标系到地面惯性坐标系的方向余弦矩阵为
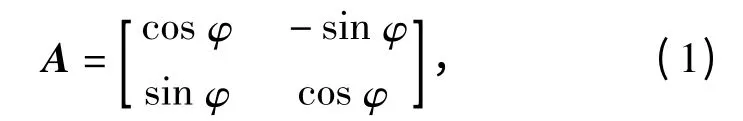
式中:φ 为连体坐标系x 轴与惯性坐标系X 轴正方向的夹角,也即为车辆的转向角。
1.2 履带接地段运动分析
如前所述,履带接地段上任意一点的剪切应力与该点的剪切位移有关,确定履带-地面之间的剪切应力是计算两侧履带牵引力、制动力、转向阻力矩等的基础,为了计算履带接地段上任意一点的剪切应力,首先需要计算履带接地段上的剪切位移量,而履带接地段上任意一点的剪切位移量则要通过对履带接地段上该点滑动速度的积分来计算。因此,首先计算两侧履带接地段的滑动速度。
1.2.1 履带接地段的滑动速度
如图1所示,当履带车辆绕转向中心OS以角速度转向时,履带的运动是由牵连运动和相对运动构成的复合运动,与在两侧履带中心线上的点O2、O1对应的履带接地段在连体坐标系下y 方向的牵连速度为
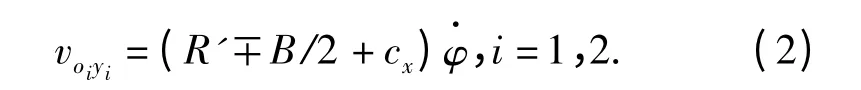
则与在两侧履带中心线上的点O2、O1对应的履带接地段在连体坐标系下y 方向的相对速度为
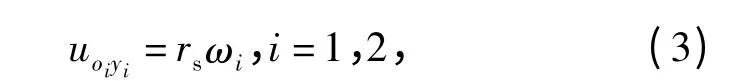
式中:rs为主动轮节圆半径;ωi为两侧主动轮角速度。
当两侧履带没有滑转和滑移时,履带接地段的瞬时转向中心O'2、O'1与O2、O1重合,此时在该点处的相对速度uoiyi等于牵连速度voiyi,该点的绝对速度为0. 当存在滑转和滑移时,点O2、O1处在连体坐标系下y 方向的绝对速度即为该点的纵向滑动速度,其表达式为
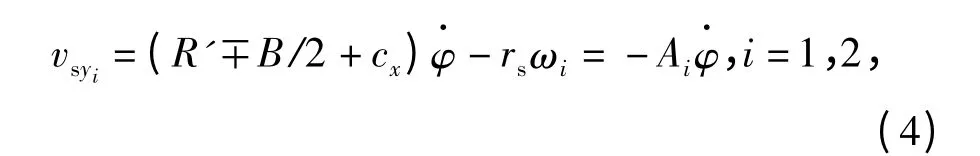
式中:Ai为两侧履带转向极的横向偏移量。
对于两侧履带接地段纵向中心线上的任意一点Pi(xi,yi),i=1,2,其在连体坐标系下的纵向滑动速度与点O1、O2相同,即为vsyi. 同样对于Pi点,履带接地段上对应于O1、O2点处的相对速度在连体坐标系下的横向分量为,也即为Pi点在连体坐标系下的横向滑动速度vsxi= -.
根据坐标变换关系,在地面参考坐标系OXY下,Pi点的横向及纵向滑动速度表示为
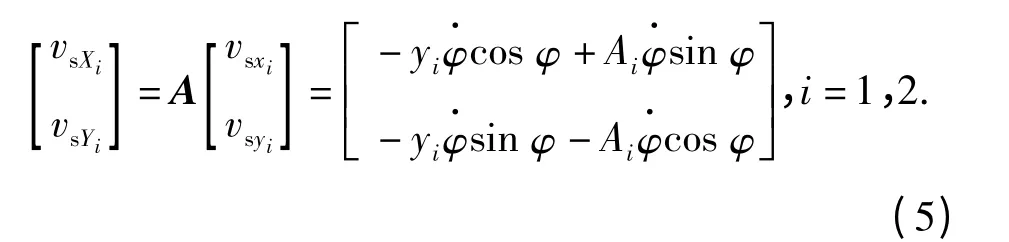
由于车辆稳态转向时的转向角速度为φ·,且Pi点到履带接地最前端的距离为L/2 +cy-s0-yi,则从两侧履带接地段最前端运动到Pi点时车辆的转向角φ 为
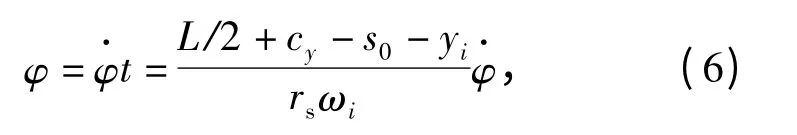
式中:t 表示稳态转向时两侧履带接地段最前端运动到Pi点时所需的转向时间,并且有t =(L/2 +cy-s0-yi)/rsωi.
1.2.2 履带接地段的剪切位移
履带接地段上各点的剪切位移沿着接地长度方向累积,至接地段后端达到最大值。
由于两侧履带接地段纵向中心线上的每一点的纵向及横向滑动速度均不同,根据定义[1],Pi点处剪切位移的横向分量jXi和纵向分量jYi分别表示为Pi点的横向及纵向滑动速度在两侧履带接地段最前端运动到Pi点时所需转向时间上的积分,其表达式为
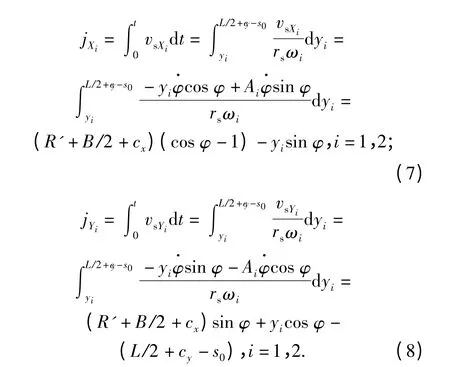
则Pi点处的合成剪切位移量为
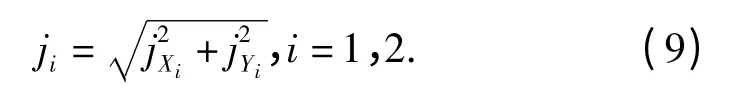
1.3 履带-地面之间相互作用力
1.3.1 履带-地面之间的法向力
当履带车辆低速转向时,往往忽略离心力的影响,但是当转向速度较高或转向半径较小时,离心力的影响就会迅速增大,为了准确的计算转向特性,应当考虑离心力的影响。
当转向过程中存在离心力时,离心力的横向分力和纵向分力会使两侧履带接地段的负荷重新分配。横向分力使得高速侧履带接地段负荷增加,低速侧履带接地段负荷减小。而离心力的纵向分力则使两侧履带的接地压力由假设的均匀分布变为履带接地段前端小后端大的梯形分布,如图2所示。两侧履带接地段的法向力表示为
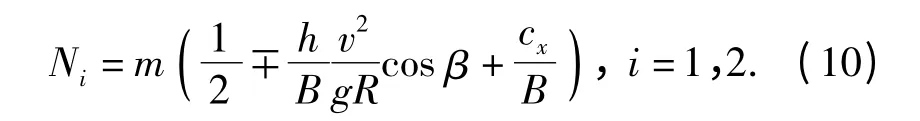
高速侧和低速侧履带接地段的接地压力为
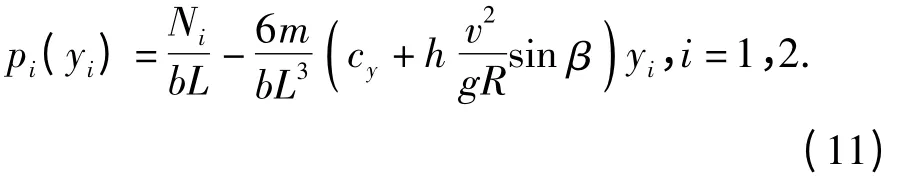
(10)式和(11)式中:v 为车辆质心处的线速度;g 为重力加速度;m 为车辆总质量;h 为车辆重心高度。
由于两侧履带负荷重新分配,在离心力纵向分力作用下,两侧履带接地段的负荷前端变小,后端变大,如图2所示。
1.3.2 履带-地面之间的牵引力与制动力
履带接地段的剪切应力与履带-地面之间的剪切位移量有关,其表达式[1]为
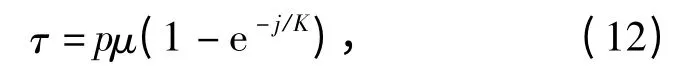
式中:p 为履带与地面之间的法向压力;μ 为履带与地面之间的摩擦系数,这里假定为常量。
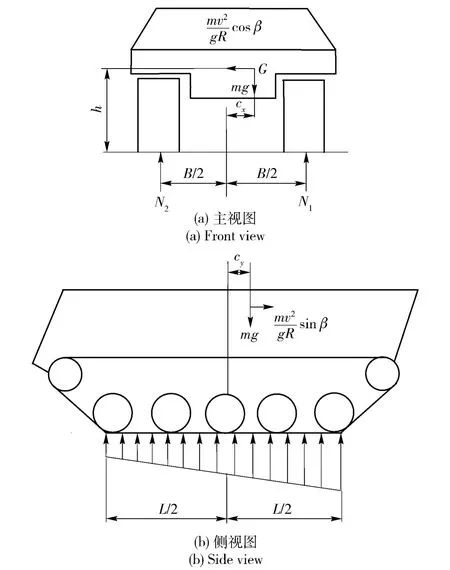
图2 两侧履带接地压力分布示意图Fig.2 Normal pressure distribution of tracks during steadystate steering of tracked vehicle
履带车辆转向时,两侧履带接地段上Pi点单位面积dA 下的切向力等于剪切应力与接地面积的乘积,其表达式为
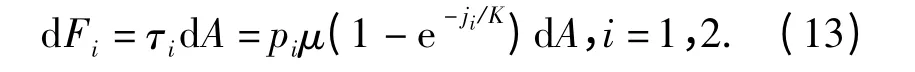
两侧履带接地段上Pi点的切向力如图1所示,其方向与该点履带-地面之间的滑动速度方向相反。则两侧履带切向力Fi的纵向分量Fyi和横向分量Fxi分别表示为单位面积下切向力的纵向及横向分量沿整个履带接地长度上的积分:
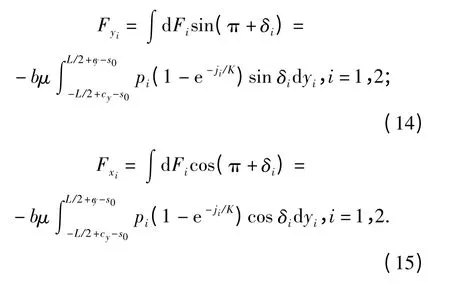
式中:δi为两侧履带的滑动速度与横向方向的夹角。根据图1中关系所示,δi的正弦及余弦函数表示为
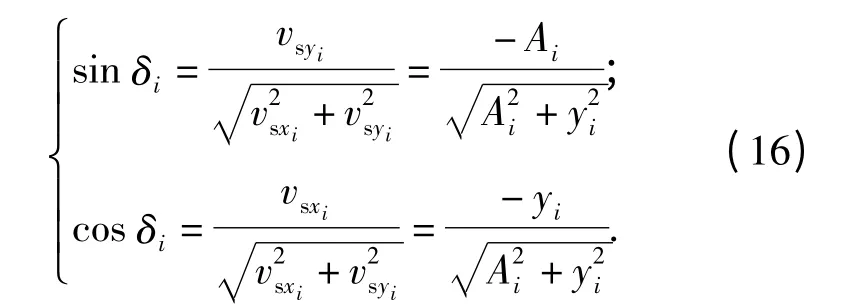
图3为履带车辆稳态转向时的受力示意图,可以看出,两侧履带与地面之间切向力的纵向分量Fyi即为车辆转向过程中两侧履带的制动力Fy1和牵引力Fy2. 而两侧履带上切向力的横向分量Fxi主要用于平衡转向时的离心力。
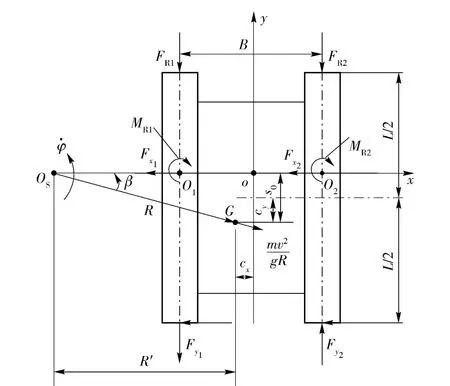
图3 稳态转向受力示意图Fig.3 Force schematicdiagram of tracked vehicle during steady-state steering
1.3.3 转向驱动力矩与转向阻力矩
从图3中看出,由两侧履带上切向力的纵向分量(即制动力和牵引力)产生的绕o 点的转向驱动力矩MDi表示为
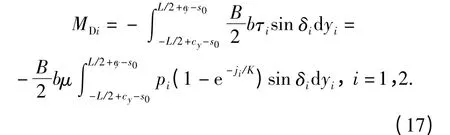
由于履带-地面之间的剪切位移及剪切应力在履带接地长度上并不相同,剪切应力的横向分量不仅产生切向力的横向分量Fxi,而且还形成绕两侧履带O1、O2点的转向阻力矩MR1和MR2,其表达式为
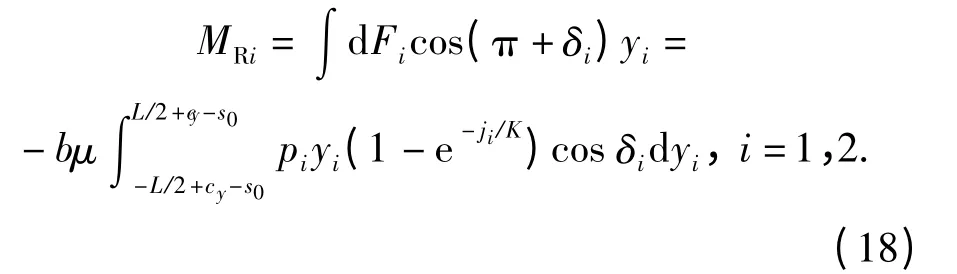
当低速转向不考虑转向离心力影响时,履带车辆稳态转向过程中总的转向阻力矩MR等于两侧履带转向阻力矩之和。当考虑转向离心力影响时,履带车辆的转向阻力矩表示为
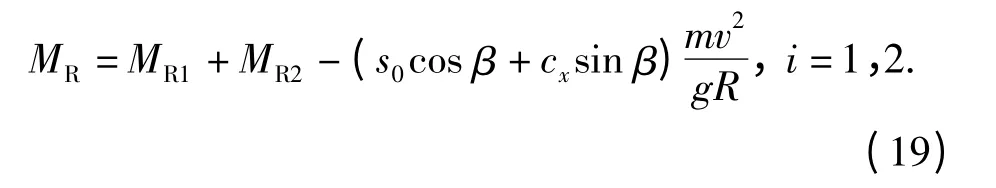
1.3.4 两侧履带的行驶阻力
两侧履带的行驶阻力FRi表示为滚动阻力系数f与两侧履带接地段法向负荷Ni的乘积,即
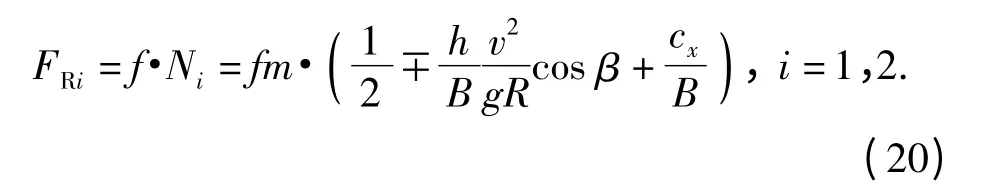
1.4 履带车辆稳态转向运动方程
履带车辆稳态转向过程中,履带上的作用力与车辆受力处于平衡状态,根据履带作用力和转矩对参考坐标系的x 轴和y 轴方向的力平衡关系,以及作用力对o 点的力矩平衡关系,推导出履带车辆稳态转向平衡方程[2]
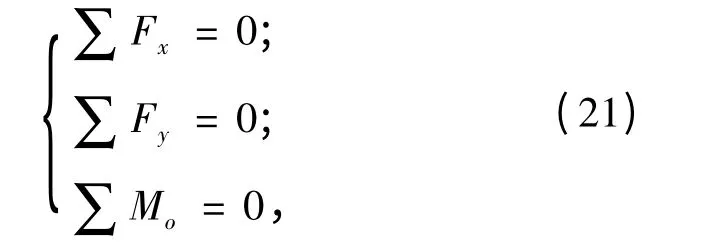
式中:∑Mo表示所有作用力对o 点的力矩之和。
展开上式,得
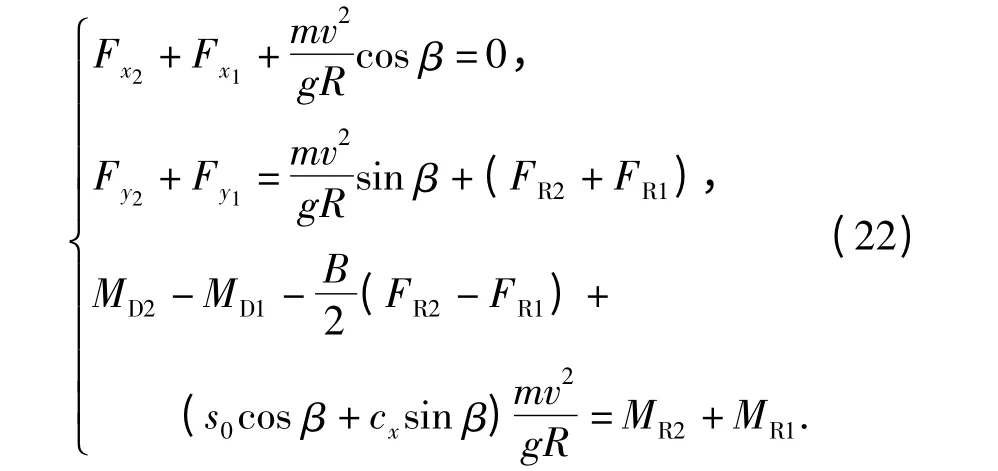
在以上转向运动控制方程中,未知量主要有两侧履带瞬时转向中心的转向极横向偏移量A2、A1和转向极的纵向偏移量s0. 当给定车辆质心线速度v和转向半径R 时,通过对(22)式的迭代计算首先确定A2、A1和s0的值,而后根据(14)式和(19)式分别计算两侧履带上的牵引力、制动力以及转向阻力矩,并由(23)式和(24)式计算高速侧履带的滑转率σ2和低速侧履带的滑移率σ1.
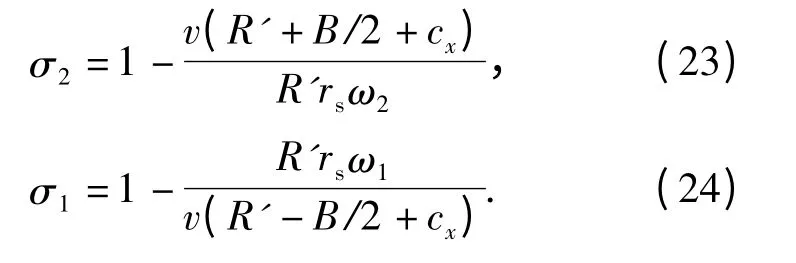
2 转向性能试验与模型验证
2.1 履带车辆转向性能试验
转向性能试验是研究履带车辆转向特性,验证转向模型可信度的有效手段。组织实施了某型履带式装甲车辆的实车试验,为了实现履带车辆转向性能参数的准确、高效测试,根据对转向运动学、动力学参数相互关系的研究,提出了一种履带车辆转向性能测试的试验方案,如图4所示。试验测试系统主要由基于NI 开发平台的测试系统、基于GPS 原理的测试系统及存储式转速转矩仪等3 套试验装置组成,该测试系统能够实现履带车辆转向过程中,两侧主动轮转速、车辆运行轨迹、行驶速度及航向角、综合传动装置两侧输出轴转速、转矩等数据的同步测试。其中NI 测试系统(见图5(a))主要利用安装在主动轮上的光电传感器测试两侧主动轮转速(见图5(b)),以及安装在炮塔顶部的数字罗盘测试车辆的航向角(见图5(c))。存储式转速转矩仪(见图5(d))主要利用安装在综合传动装置输出轴上的应变片及转速计测试两侧输出轴两端的转速和转矩。GPS 测试系统主要利用安装在炮塔顶部的移动站分系统(见图5(e))和位于地面的基准站分系统(见图5(f))测试转向运行轨迹、行驶速度及航向角。由于试验中采用了具有二次差分功能的高精度GPS 测试系统,可以连续、准确测试出车辆的行驶轨迹(即转向半径)、车速和航向角等行驶参数。
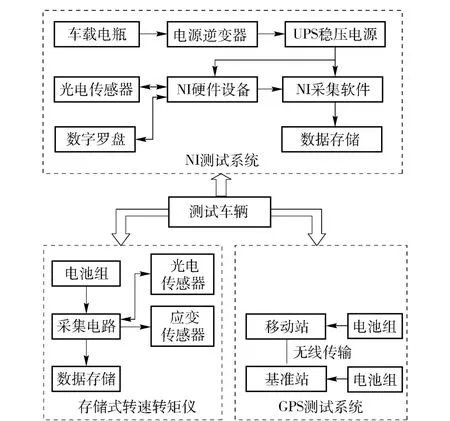
图4 履带车辆转向性能试验测试方案Fig.4 Experimental scheme of tracked vehicle for steady-state steering

图5 实车转向试验测试装置Fig.5 Experimental equipment for steady-state steering of tracked vehicle
根据综合传动装置两侧输出轴转矩Mo2和Mo1可以求得两侧主动轮上的转矩Ms2和Ms1. 考虑到主动轮与履带之间啮合效率、侧减速器传动效率以及侧减速器减速比等因素,可根据下式求出两侧履带上的牵引力Fy2和制动力Fy1.
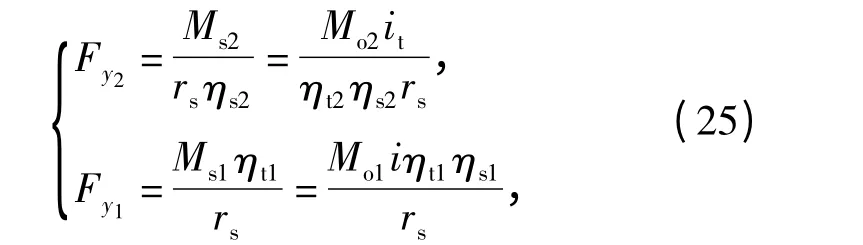
式中:Ms2、Ms1分别表示高速侧和低速侧主动轮上的转矩;Mo2、Mo1分别表示高速侧和低速侧综合传动装置输出轴上的转矩;it表示侧传动比;ηt2、ηt1为两侧履带综合传动装置输出轴到主动轮的侧传动效率,取0.97;ηs2、ηs1为两侧主动轮与履带之间啮合效率,取0.92.
图6给出了履带车辆在砂土路面以2 挡6.66 km/h的行驶速度,以18.34 m 的转向半径转向时,两侧履带速度以及牵引力、制动力随时间变化的试验结果。
2.2 转向模型的试验验证
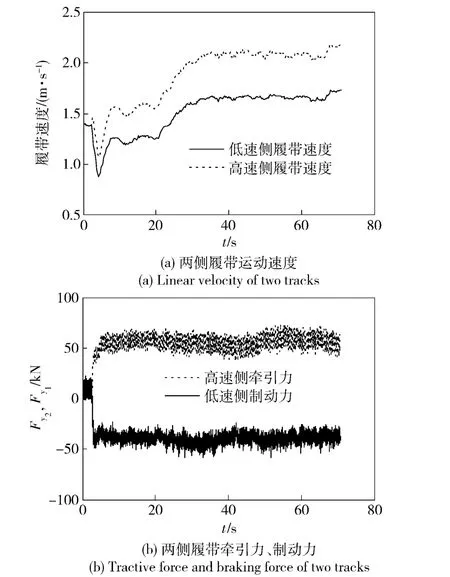
图6 履带车辆转向过程中的部分测试结果Fig.6 Partial experimental results for steady-state steering of tracked vehicle
以某型履带式装甲车辆为对象,基于建立的履带车辆转向动力学模型,仿真分析履带车辆的稳态转向性能,并根据试验结果对转向模型进行验证。该履带车辆采用了综合传动装置,转向机构的调节部件为流量可调的静液泵马达系统,可以实现差速式转向。车辆的基本参数以及相关的地面参数见表1所示。
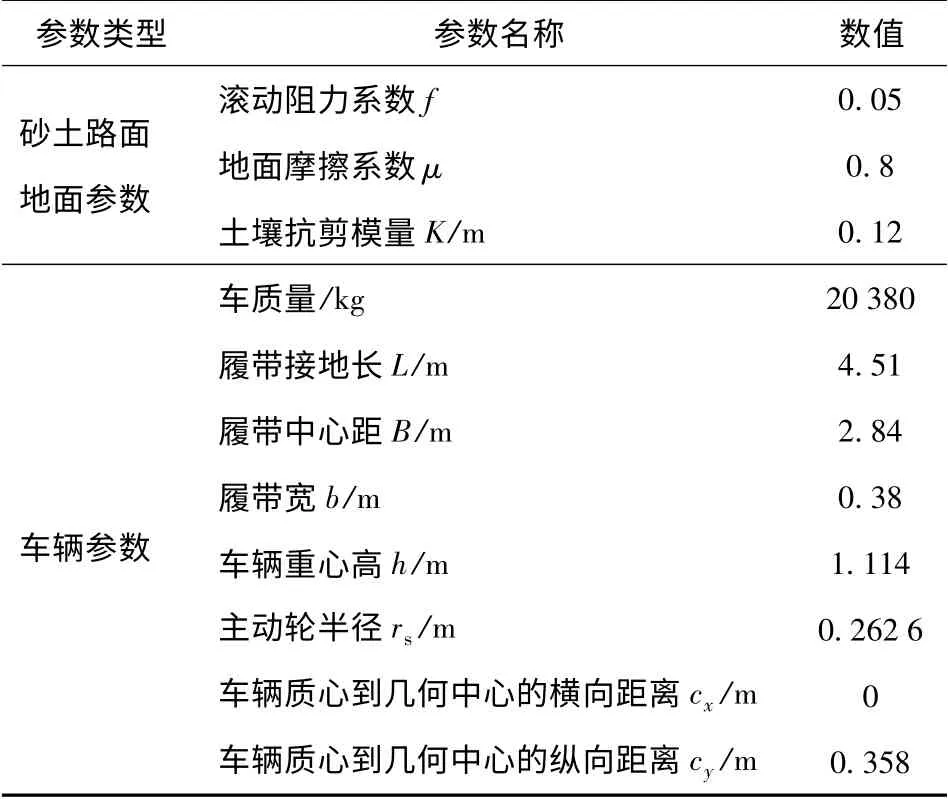
表1 转向模型计算参数Tab.1 Vehicle and soil parameters and values
为了验证转向模型的准确性,进行了不同转向半径条件下,转向运动学及动力学特性的数值计算与试验结果的分析与对比。砂土路面条件下,履带车辆的转向运动学及动力学特性的计算结果与试验结果对比如图7~图10 所示。
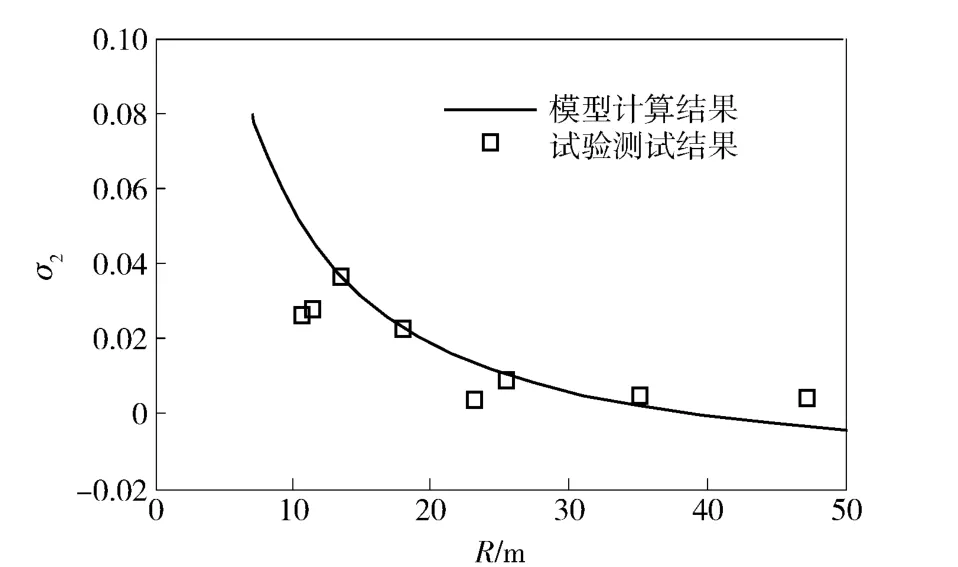
图7 高速侧履带滑转率σ2 随实际转向半径R的变化关系曲线Fig.7 Relation between slippage rate of track on high speed side σ2 and R
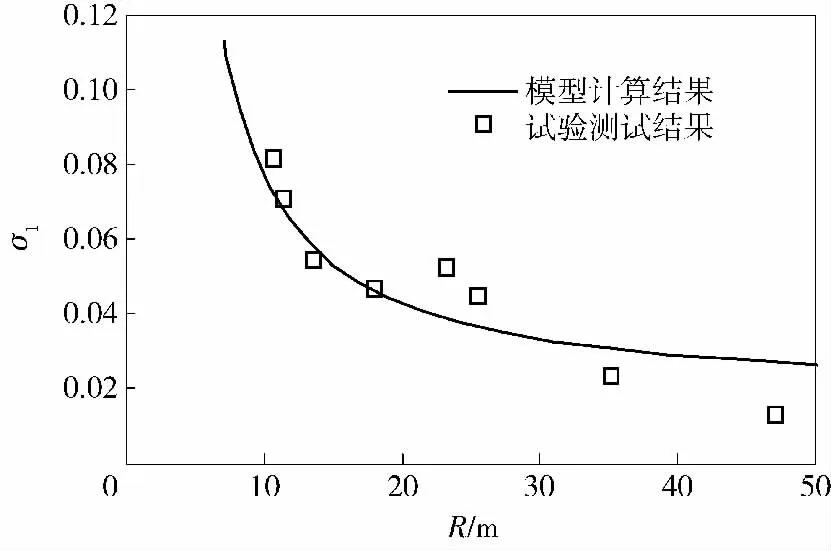
图8 低速侧履带滑移率σ1 随实际转向半径R的变化关系曲线Fig.8 Relationship between skid rate of track on low speed side σ1 and R
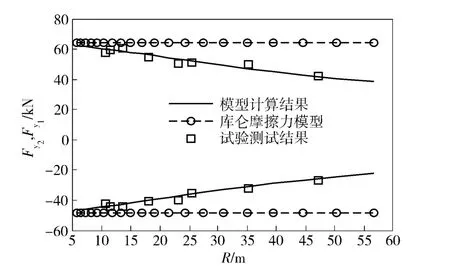
图9 牵引力Fy2、制动力Fy1随实际转向半径R的变化关系曲线Fig.9 Relationship among traction force Fy2,braking force Fy1 and R
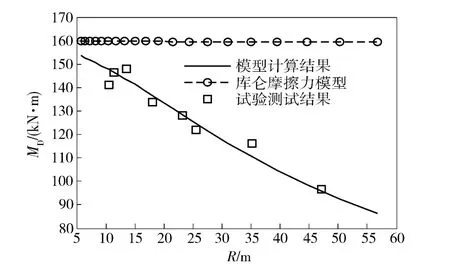
图10 转向驱动力矩MD 随实际转向半径R 的变化关系曲线Fig.10 Relationship between steering driving torque MD and R
图7、图8分别为履带车辆转向时,高速侧履带滑转率σ2及低速侧履带滑移率σ1的模型计算结果与试验结果随车辆实际转向半径R 的变化关系曲线。从结果对比可见,两侧履带滑转率和滑移率的计算结果与试验结果从总体变化趋势上具有良好的一致性。滑转率和滑移率均具有随履带车辆转向半径的增大逐渐减小的变化趋势。
图9、图10 分别为履带车辆转向时,两侧履带牵引力Fy2、制动力Fy1以及转向驱动力矩MD的模型计算结果与试验结果随车辆实际转向半径R 的变化关系曲线。从图9、图10 中可看出,履带车辆转向模型的计算结果与试验结果具有很好的一致性。并且模型计算结果反映了两侧履带牵引力与制动力、转向驱动力矩均随转向半径增大而逐渐减小的变化趋势,这与试验数据点的变化趋势完全一致。而基于库仑摩擦力的转向模型却无法体现转向动力学参数随转向半径的变化趋势,因而与试验测试结果有较大的差异。
为了进一步验证转向模型的准确性,表2给出了履带车辆在砂土路面以两个不同半径转向时,转向性能参数的计算结果与试验结果对比。
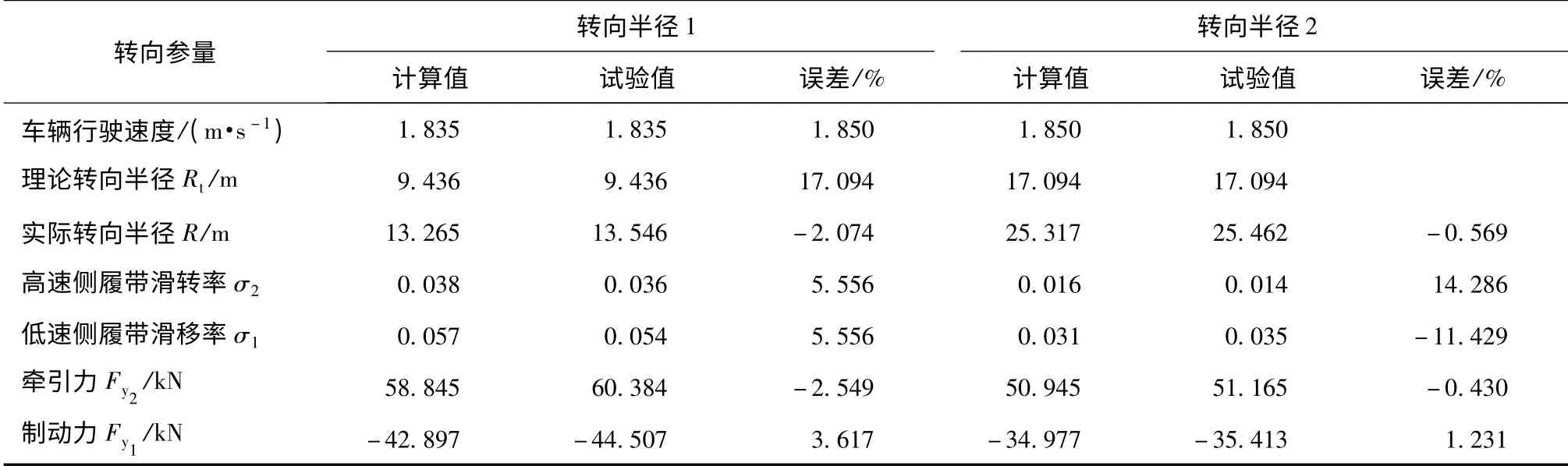
表2 试验结果与仿真结果的对比Tab.2 Comparison of experimental and calculated results
在表2中,以试验测得的稳态转向时的车辆行驶速度和理论转向半径为履带车辆动力学模型的输入条件进行计算。从表2中结果对比可以看出:当考虑履带滑动时,实际转向半径计算结果与试验结果误差约为2%左右;两组数据的两侧履带滑转率和滑移率计算结果与试验结果误差小于15%;履带牵引力及制动力计算结果与试验结果的误差小于4%.
3 转向性能分析
由前述分析可知,当车辆在不同车速及转向半径下行驶时,会造成车辆转向时离心力的变化。离心力的改变会造成两侧履带接地压力的重新分布,并进而改变两侧履带转向时的牵引力、制动力以及转向阻力矩等。
为了分析履带车辆的转向性能,分别计算了履带车辆以不同行驶速度和半径转向时的转向运动学及动力学参数。履带车辆转向时的车速v 分别取为0.1 m/s、2.0 m/s、4.0 m/s、6.0 m/s、8.0 m/s. 相对转向半径的变化范围为1 <ρ <100.
图11 所示为转向极纵向相对偏移量a(a =s0/(L/2))随相对转向半径及车速的变化趋势,可以看出,转向极纵向相对偏移量随相对转向半径的增大而减小,而随着转向时车速的提高而增加。这主要是由于转向半径越小、转向车速越高,离心力的横向分量会显著增加。此时,为了平衡逐渐增大的履带车辆横向分力,转向极的纵向偏移量就会相应增加。当转向极纵向相对偏移量大于1 时,履带车辆的转向中心在纵向方向上已经位于履带接地段前端的外侧,表明履带车辆处于横向失稳状态。图11 中当车辆在8 m/s 的速度下以小半径转向时,转向极纵向相对偏移量的值就会出现大于1 的现象,这表明车辆此时会出现横向失稳状态。因而,可以用转向极纵向相对偏移量a 作为车辆产生转向横向失稳的判据。
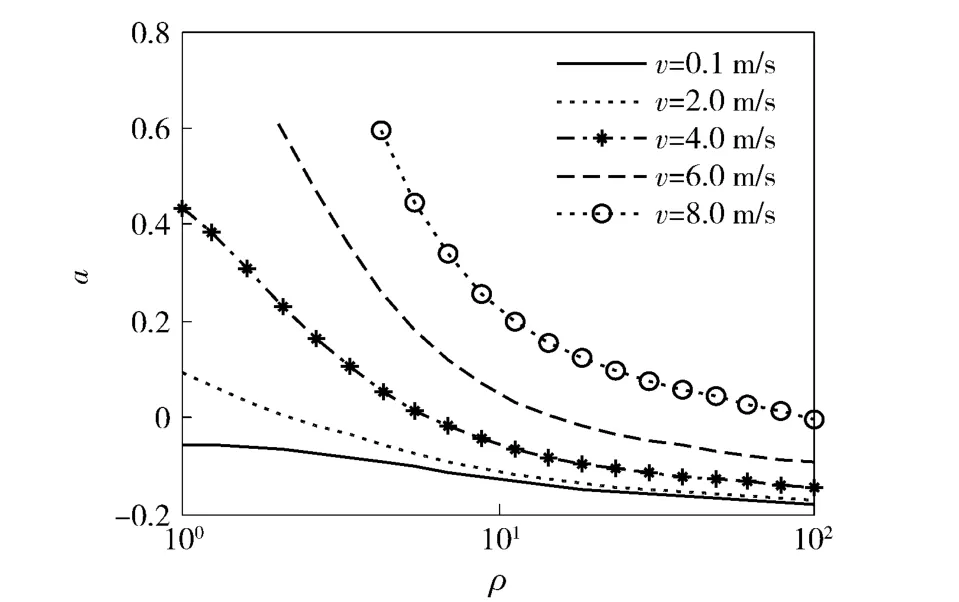
图11 转向极纵向相对偏移量a 随相对转向半径ρ及车速v 变化趋势Fig.11 Relationship among relative longitudinal offset of steering-pole a ,ρ and v
图12 为两侧履带的牵引力Fy2、制动力Fy1随相对转向半径及车速的变化趋势。从总体上来看,两侧履带的牵引力和制动力具有随相对转向半径的增大而减小的趋势。当高速转向时,由于离心力的影响,两侧履带上的牵引力和制动力要比低速转向时小,在转向半径较小时,离心力对低速侧制动力的影响更为显著。
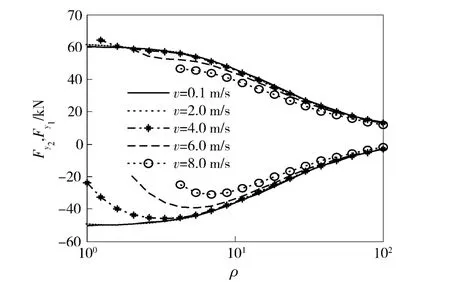
图12 牵引力Fy2、制动力Fy1随相对转向半径ρ 及车速v 变化趋势Fig.12 Relationship among traction force Fy2,braking force Fy1,ρ and v
图13 为转向阻力矩随转向半径及车速的变化趋势。从图中看出,转向阻力矩随相对转向半径增加而减小。高速转向时,履带车辆的转向阻力矩要小于低速转向时,这主要是由于随着转向时车速的增加,转向离心力的影响对于车辆转向来说是有利的,能够有助于履带车辆的转向,这种影响在转向半径较小时更为明显。
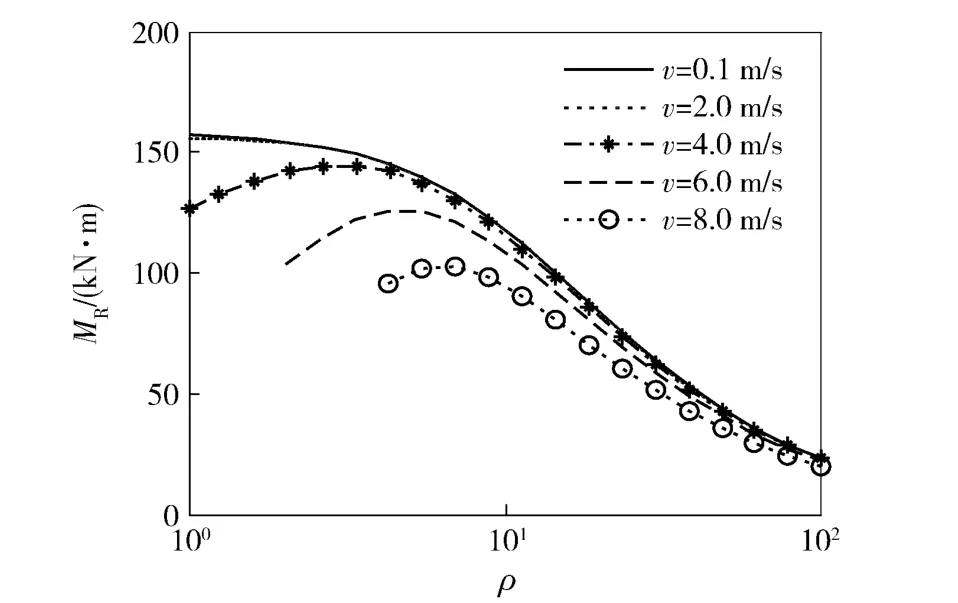
图13 转向阻力矩MR 随相对转向半径ρ及车速v 变化趋势Fig.13 Relationship among steering resistance torque MR,ρ and v
从图11 ~图13 中还可以看出,当转向时车速v=2.0 m/s 时,转向极纵向偏移量、两侧履带牵引力、制动力以及转向阻力矩的计算结果与v =0.1 m/s时是一致的,表明此时由于车速较低,转向离心力的影响可以忽略不计。而随着车速的增加,尤其在小半径转向时,转向离心力的影响越显著,因而在进行履带车辆的高速转向尤其是高速小半径转向的转向性能分析时就必须要考虑离心力的影响。
4 结论
本文建立了考虑履带打滑以及转向离心力影响的履带车辆稳态转向模型,通过实车道路试验测试结果与计算结果的对比验证了履带车辆转向模型的准确性,并对履带车辆不同转向条件下的转向性能进行了分析,主要结论如下:
1)根据剪切应力-剪切位移关系模型推导了两侧履带牵引力、制动力及转向阻力矩等的计算公式,建立了考虑履带滑移及离心力影响的履带车辆稳态转向模型。试验结果与计算结果的一致性证明了履带车辆转向模型的准确性。
2)对比研究了基于剪切应力-剪位移关系转向模型计算结果与基于库仑摩擦力转向模型计算结果的差异。结果表明:基于库仑摩擦力转向模型计算的两侧履带牵引力、制动力以及转向阻力矩不随转向半径的增大而改变,这与实际情况不符。而基于剪切应力-剪位移关系模型的计算结果与试验结果具有很好的一致性,所反映的两侧履带牵引力与制动力、转向阻力矩等随转向半径增大时的变化趋势与试验数据一致。
3)研究了履带车辆转向运动学及动力学特性随转向半径及转向车速的变化规律。转向极纵向相对偏移量a 随转向半径的增大而减小,随车速的增加而增加,当车辆高速小半径转向时,会导致a >1,此时车辆处于横向失稳状态,因而,可以用a 作为车辆转向横向失稳的判据。两侧履带牵引力、制动力以及转向阻力矩随车速的增大而减小,这主要是由于转向过程中,随着车速的增加,离心力对转向性能的影响越显著的结果。
References)
[1]Wong J Y. Theory of ground vehicles[M]. 3rd ed. New York:John Wiley & Sons,2001.
[2]程军伟. 采用综合传动装置的军用履带车辆转向研究[D].北京:装甲兵工程学院,2007.CHENG Jun-wei. Study on steering of military tracked vehicle equipped with power-shift steering transmission[D]. Beijing:Academy of Armored Force Engineering,2007.(in Chinese)
[3]程军伟,高连华,王良曦,等. 基于打滑条件下的履带车辆高速转向分析[J]. 车辆与动力技术,2006(1):45 - 48.CHENG Jun-wei,GAO Lian-hua,WANG Liang-xi,et. al. Analysis of tracked vehicles steering at a high speed considered tracks’skid and slip[J]. Vehicle & Power Technology,2006(1):45 -48. (in Chinese)
[4]Said A M,Lakmal D S,Kaspar A. Track-terrain modelling and traversability prediction for tracked vehicles on soft terrain[J].Journal of Terramechanics,2010,47(3):151 -160.
[5]Ehlert W,Hug B,Schmid I C. Field measurements and analytical models as a basis of test stand simulation of the turning resistance of tracked vehicles [J]. Journal of Terramechanics,1992,29(1):57 -69.
[6]荆崇波,魏超,李雪原,等. 履带车辆差速转向机构转向过程动态特性的试验方法[J]. 农业工程学报,2009,25(7):62 -66.JING Chong-bo,WEI Chao,LI Xue-yuan,et al. Test method of steering dynamic characteristics of differential steering mechanism of tracked vehicle[J]. Transactions of the CSAE,2009,25(7):62 -66. (in Chinese)
[7]曹付义,刘洋,周志立. 履带车辆软地面稳态转向驱动力计算模型[J]. 河南科技大学学报:自然科学版,2014,35(2):29 -32.CAO Fu-yi,LIU Yang,ZHOU Zhi-li. Steady turning thrust calculation model of tracked vehicle on soft terrain [J]. Journal of Henan University of Science and Technology:Natural Science,2014,35(2):29 -32. (in Chinese)
[8]Wong J Y,Chiang C F. A general theory for skid steering of tracked vehicles on firm ground[J]. Journal of Automobile Engineering,2001,215(3):343 -355.
