脉冲多普勒引信抗有源噪声干扰性能研究

李泽，栗苹，郝新红，闫晓鹏，王建涛

(北京理工大学 机电工程与控制国家重点实验室，北京100081)

0 引言

脉冲多普勒(PD)引信是一种利用多普勒效应工作的脉冲引信，它集合了脉冲引信所具有的测距和连续波多普勒引信所具有的测速特性，具有较好的抗地、海杂波和背景干扰能力及良好的低空作战性能［1-4］。但是在现代战场的复杂电磁环境中，引信干扰机和强电磁能武器对PD 引信构成了严重威胁，研究并提高PD 引信抗干扰性能是提高其战场生命力的有效途径。目前针对无线电引信抗干扰性能量化分析方法的研究，主要集中在模糊函数切割法［5-7］、计算干扰信号作用下引信启动概率［8］和处理增益方法［9-12］等。

文献［7］提出了一种基于模糊函数切割法的PD 引信抗干扰性能测度方法，刻画了PD 体制本身固有的抗干扰性能，但不能获得不同干扰样式对引信的干扰效果及干扰机理。文献［8］提出引信启动概率受外界干扰的影响程度可作为评估引信抗干扰性能的一个指标，但该方法只适用于具有概率分布特性的噪声干扰。文献［9 -12］采用处理增益方法定量分析了超宽带以及伪码复合体制引信的抗干扰性能。处理增益是基于干扰波形样式的表征参量，可以方便地对比不同干扰样式对引信的干扰效果，以获取引信敏感干扰波形样式，从而为引信抗干扰设计提供理论依据，但针对PD 体制引信抗干扰性能的量化分析还未见报道。

为此，本文以处理增益为表征参量，基于功率谱定量研究PD 引信抗射频噪声、噪声调幅和噪声调频干扰的能力，揭示有源噪声干扰对其作用机理，从而为提高PD 引信抗有源噪声干扰性能而进行的参数优化设计提供理论依据。

1 PD 引信工作原理

PD 引信按照相干检测的方式可分为两类:一类是脉冲对脉冲相干检测的PD 引信，将发射信号的一部分，经微波延迟线延时，作为回波信号进行相干检测的基准信号;另一类是脉冲对连续波相干检测的PD 引信，发射机发射射频脉冲时，还提供一个与射频完全相干的相参信号给混频器，作为与回波脉冲信号进行相干检测的基准信号。

本文以脉冲对连续波相干检测的PD 引信为例，重点研究PD 引信抗有源噪声干扰的性能。PD引信的原理框图如图1所示，其工作原理为:用脉冲对载波进行调制，调制后的射频脉冲由发射天线向外辐射。回波信号经带通滤波器滤掉带外噪声后，进入混频器与载波混频，获得受多普勒信号调制的双向视频信号;视频信号经视频放大后，进入距离门选通电路，当回波延迟达到预定的距离延迟时，才有输出信号;并将距离门的输出信号送至多普勒信号处理模块进行处理，若满足起爆条件，则产生启动信号，触发执行机构。距离门选通与多普勒信号处理相当于对回波信号进行相关处理，当回波信号与距离门信号完全相关时，多普勒输出信号幅度最大。

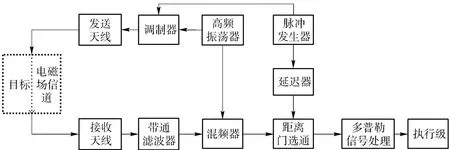
图1 PD 引信的原理框图Fig.1 Block diagram of PD fuze

PD 引信发送的射频脉冲信号为

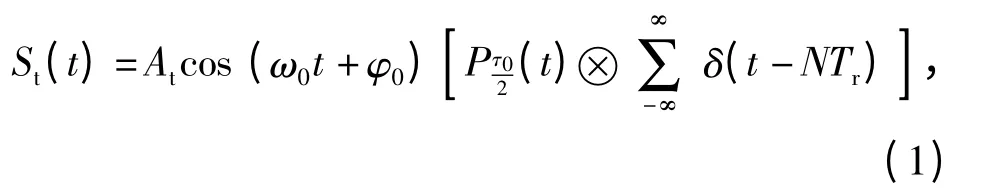
式中:At为射频脉冲幅度;ω0为载波角频率;φ0为初始相位;是宽度为τ0、幅度为1 的脉冲;Tr为脉冲重复周期;定义为脉冲占空比;N 为整数;δ(t)为狄利克雷函数。

2 有源噪声干扰下PD 引信处理增益定量数学模型

2.1 射频噪声干扰下PD 引信的处理增益

由(1)式，PD 引信目标回波信号可表示为

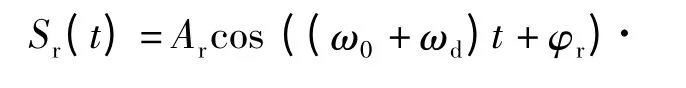
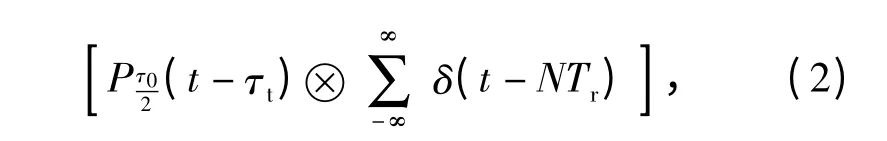
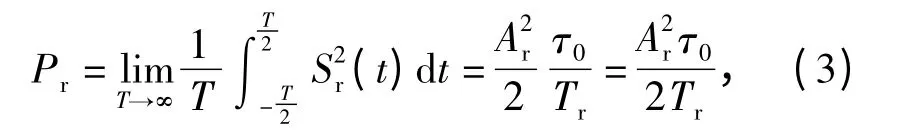
式中:T 为积分上下限的参量。

射频噪声干扰信号［13］可以表示为

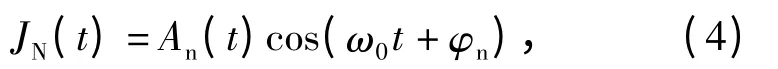
式中:包络过程An(t)服从瑞利分布;相位过程φn服从［0，2π)均匀分布，且与An(t)独立。则在射频噪声存在的情况下，实际回波信号变为Sr(t)+JN(t). 射频噪声的功率谱经常采用瞄准引信信号频率的矩形功率谱表示:

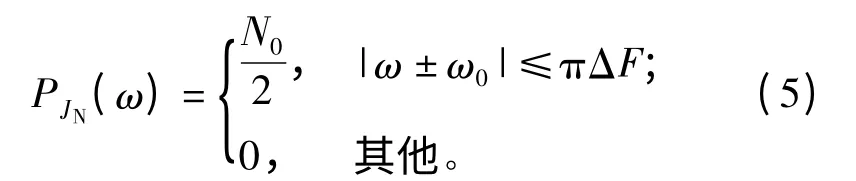
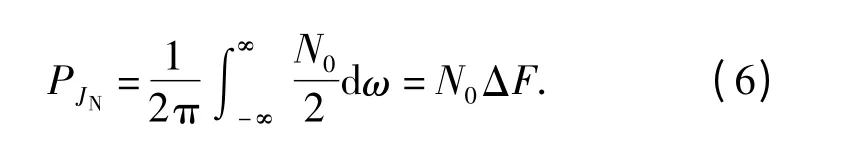
因此，系统输入信干比为

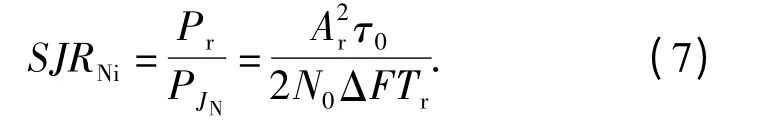
回波由引信接收天线接收后，首先会通过一个中心频率为载频ω0的带通滤波器，用以滤除带外噪声。射频噪声JN(t)经过带通滤波器后变为窄带噪声JN1(t)，可见混频器输入端的噪声带宽与已调信号带宽相同。单边带等效带宽约为的功率谱变为

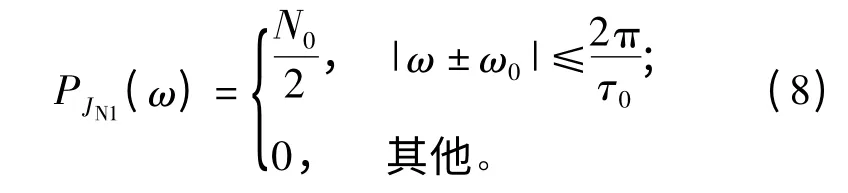
回波信号经带通滤波及混频后输出的中频信号为

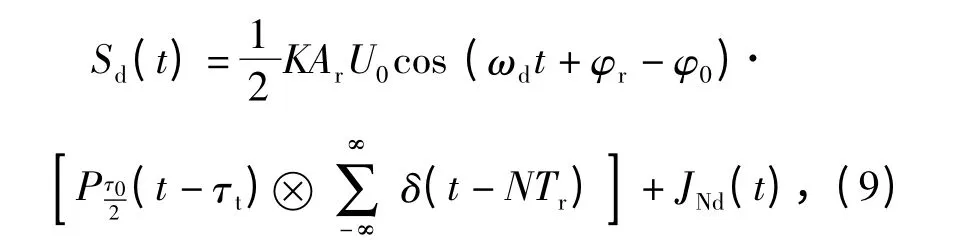
式中:JNd(t)为混频输出后的噪声项;K 为混频器系数;U0为载波幅度。由随机过程理论，可得JNd(t)的功率谱为

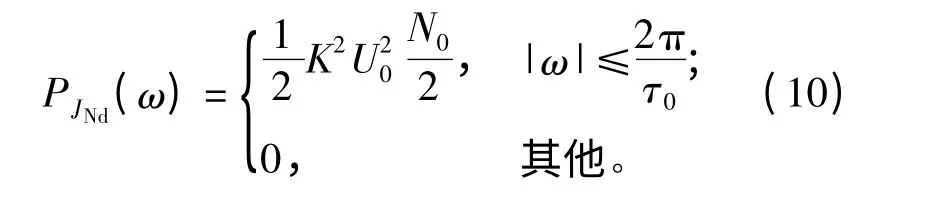
则中频信号Sd(t)经过后一级距离门选通后的输出SdR(t)为

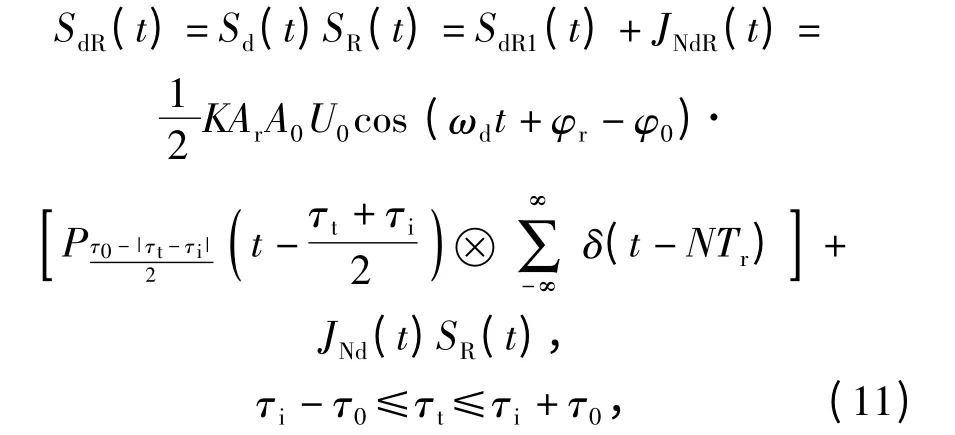
式中:A0为本地距离门信号的幅值;τi是距离门的预定延迟;SdR1(t)是距离门选通后的目标回波成分，其频谱为

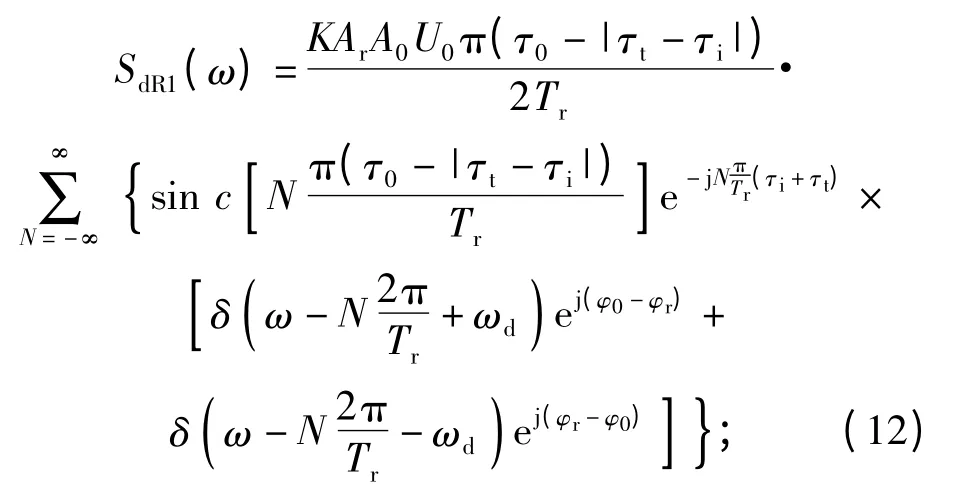
JNdR(t)是距离门选通后的噪声成分;为距离门选通信号，其傅里叶级数的表示形式为

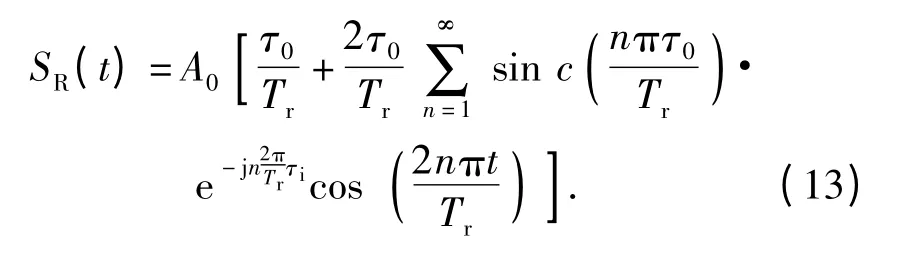
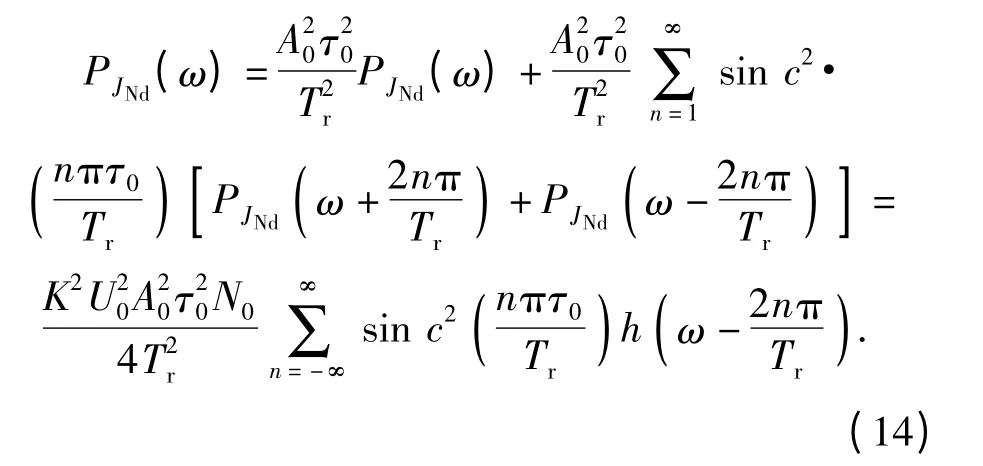
距离门输出信号，首先要经过多普勒滤波器组，获得基带多普勒信号供后续信号处理。对PD 引信而言，距离门和基带多普勒滤波器共同完成了对目标信号的相关检测。本文所推导的正是接收回波至基带多普勒滤波这一过程的处理增益。

基带多普勒滤波的传递函数可表示为

式中:Fd为基带多普勒滤波器的截止频率。

由(12)式、(14)式和(15)式的频谱分析可得射频噪声信号作用下基带多普勒滤波器的输出信号为

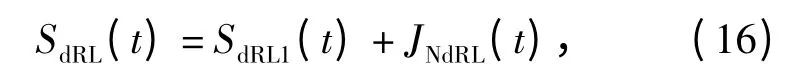
式中:SdRL1(t)为输出的有用信号成分;JNdRL(t)为输出噪声。

SdRL1(t)时域表达式为

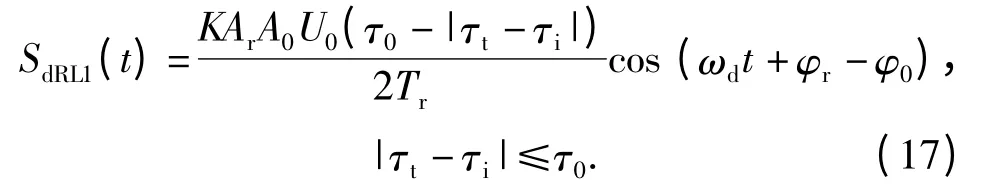
当τt=τi时，输出的有用信号达到(18)式所示的最大功率:

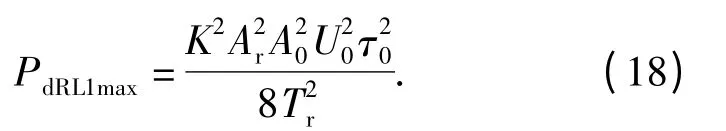
JNdRL(t)的功率谱为

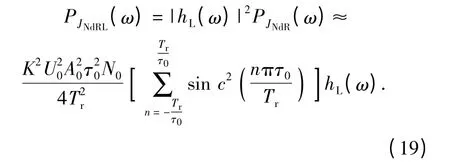
故输出噪声的平均功率为

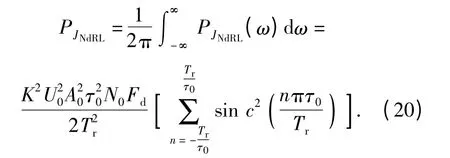
由(18)式和(20)式，基带多普勒滤波器输出的最大信干比为

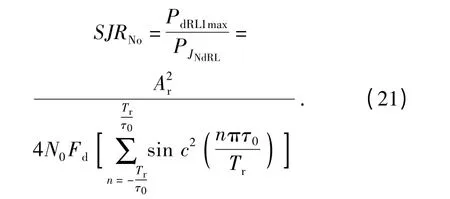
因此，可得射频噪声干扰作用下，PD 引信的系统处理增益量化表达式为

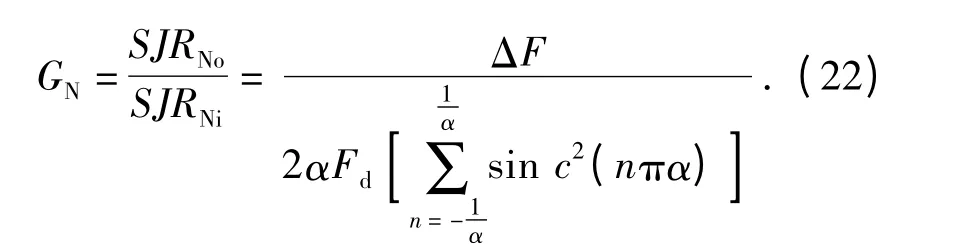
2.2 噪声调幅干扰下脉冲多普勒引信的处理增益

噪声调幅干扰信号可以表示为［13］

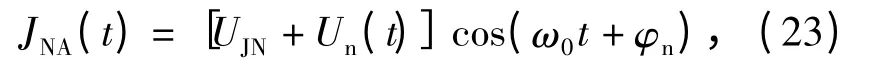
式中:调制噪声Un(t)是均值为0、方差为σ2n、在区间［-UJN，+ ∞)分布的广义平稳随机过程;φn为［0，2π)均匀分布的随机变量，且与Un(t)独立;UJN为噪声调幅干扰信号的载波幅值。

噪声调幅干扰信号的功率谱为

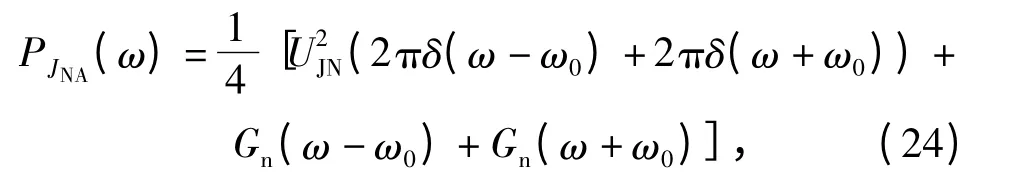
则干扰信号的平均功率为

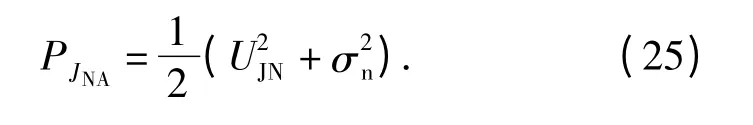
由(3)式和(25)式，可得噪声调幅干扰信号作用下系统的输入信干比为

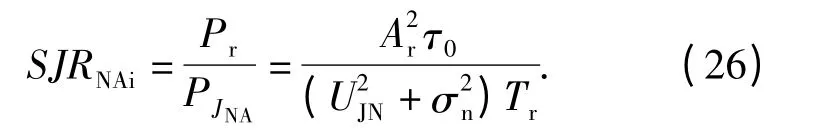
噪声调幅干扰信号经过带通滤波器后，带外噪声被滤掉，功率谱则变为

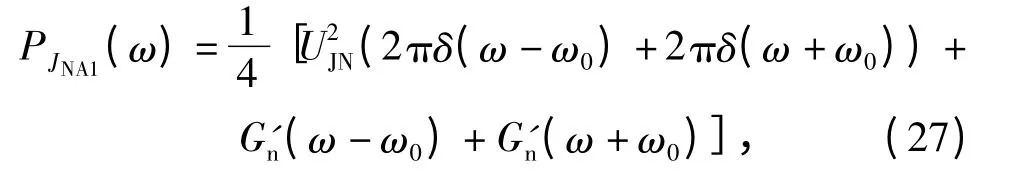
噪声调幅干扰信号经过带通滤波及混频后，输出信号为

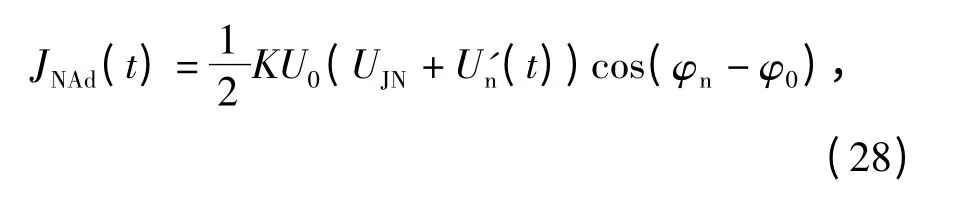
其功率谱为

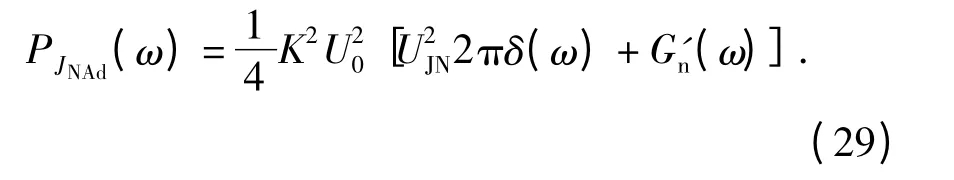
再经过距离门选通后，其输出信号为

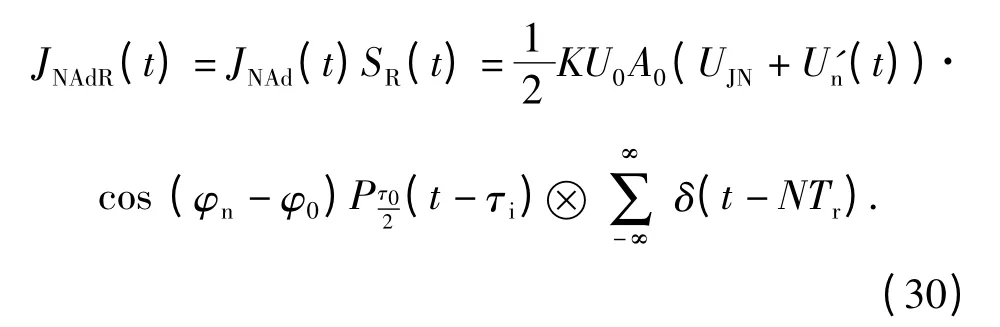
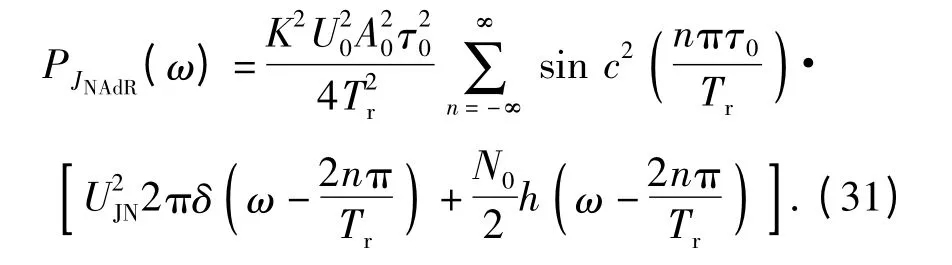
噪声调幅干扰信号经过距离门选通后，进入基带多普勒滤波器，其传递函数在(15)式中已经提到。

故可得到噪声调幅干扰信号作用下基带多普勒滤波器的输出信号JNAdRL(t)的功率谱为

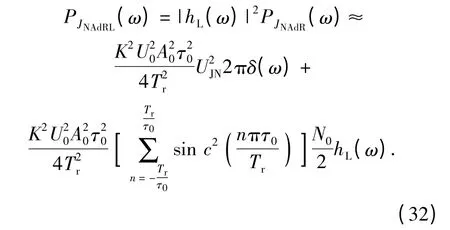
基带多普勒滤波器输出的干扰信号平均功率为

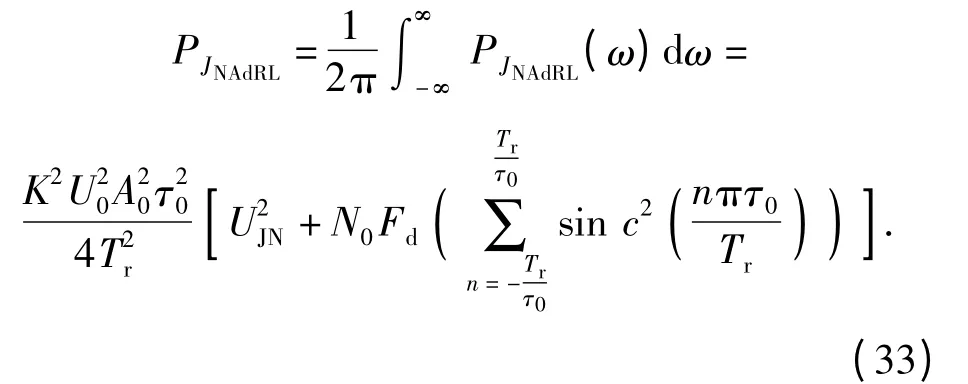
由(18)式和(33)式，可得系统相关检测后输出的最大信干比为

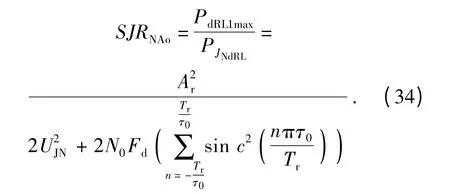
因此，噪声调幅干扰作用下系统的处理增益量化表达式为

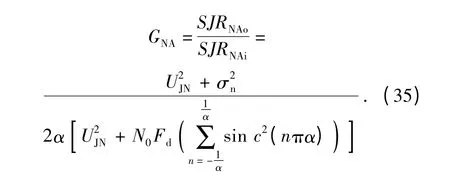
2.3 噪声调频干扰下PD 引信的处理增益

噪声调频干扰信号可以表示为［13］

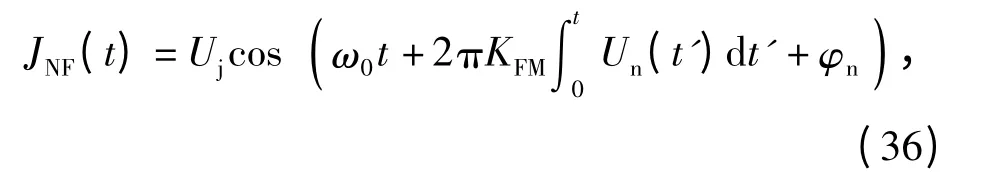
式中:调制噪声Un(t)是均值为0、方差为σ2n的广义平稳随机过程;φn为［0，2π)均匀分布的随机变量，且与Un(t)独立;Uj、ω0、KFM分别为噪声调频干扰的振幅、中心角频率和调制频率。

令fde=KFMσn为有效调频带宽为有效调频指数(ΔFn是调制噪声的等效带宽)，且mfe≫1 对于噪声调频干扰恒成立，则噪声调频干扰信号的功率谱如(37)式所示。

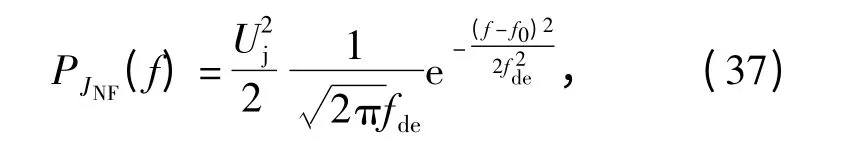
式中:f 为频率;f0为噪声调频干扰的中心频率。

噪声调频干扰信号的平均功率为

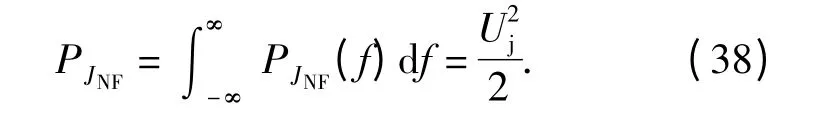
由(3)式和(38)式，可得噪声调频干扰信号作用下系统的输入信干比为

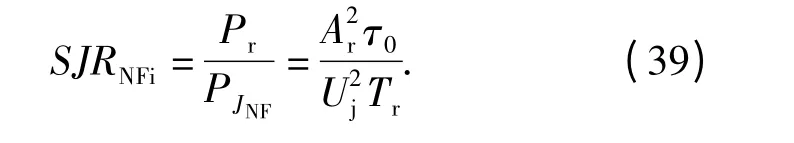
噪声调频干扰信号的瞬时频率随调制噪声电压变化，经过带通滤波器，只有频率处于内的干扰信号可以通过，故干扰信号功率谱变为

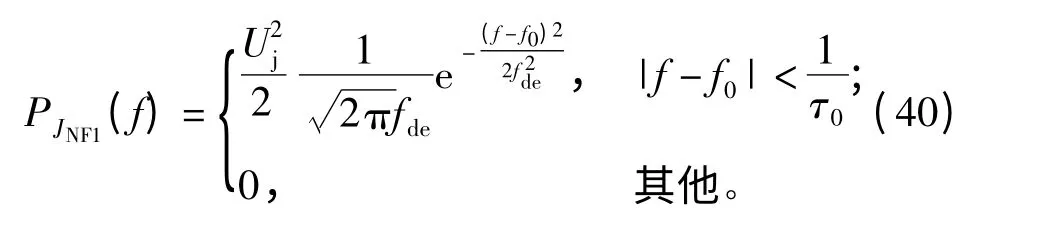
噪声调频干扰信号经带通滤波及混频后的输出信号变为

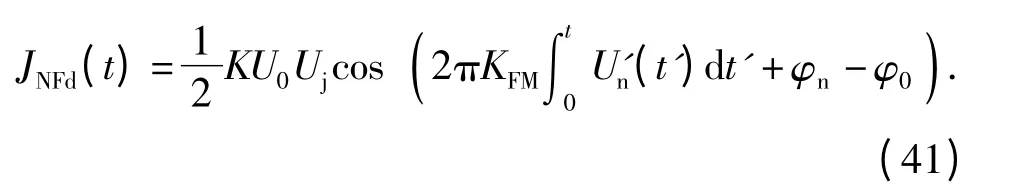
其功率谱为

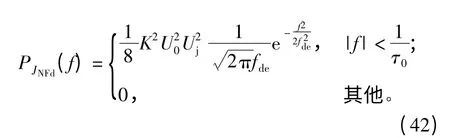
噪声调频干扰信号再经距离门选通后输出的信号为

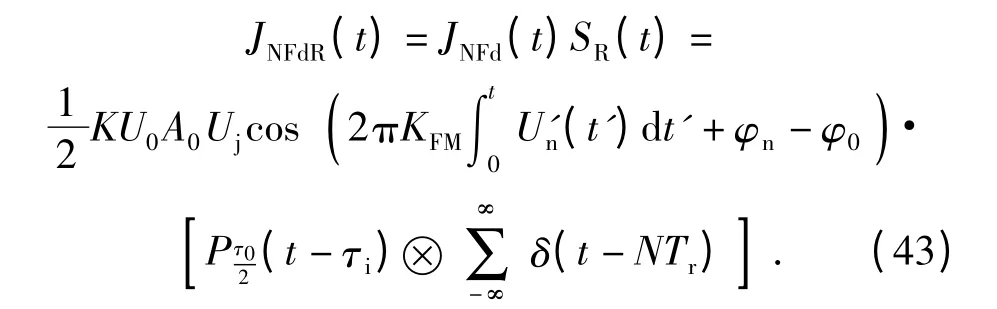
同于(14)式分析，设 hF(ω)=的功率谱可以表示为

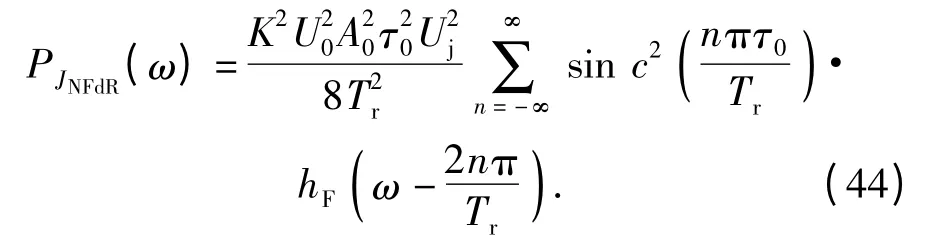
噪声调频干扰信号经过距离门选通后，进入基带多普勒滤波器，其传递函数hL(ω)在(15)式中已经提到。但由于PJNFdR(ω)在［-2πFd，2πFd］处的功率谱表征很困难，为简化推导，将在［- 2πFd，2πFd］内的功率谱等效取值为的均匀分布功率谱

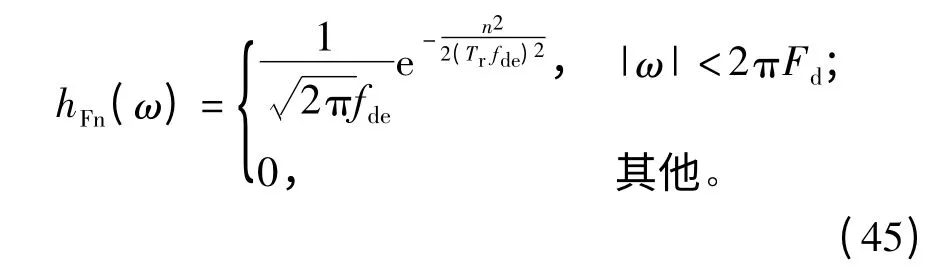
经仿真验证，上述等效与实际情况较为相近。

故可得调频干扰信号作用下，基带多普勒滤波器的输出信号JNFdRL(t)的功率谱

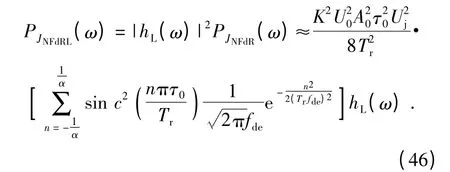
则基带多普勒滤波器的输出信号JNFdRL(t)的平均功率为

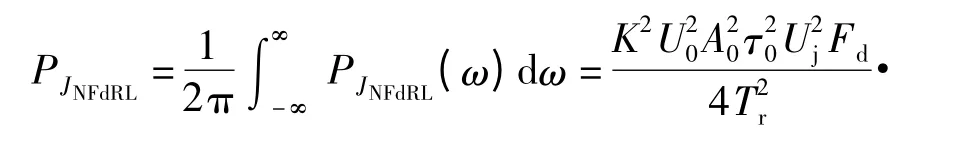
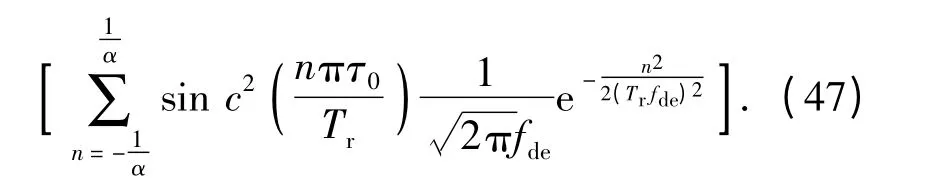
由(18)式和(47)式，可得噪声调频干扰信号作用下系统输出的最大信干比为

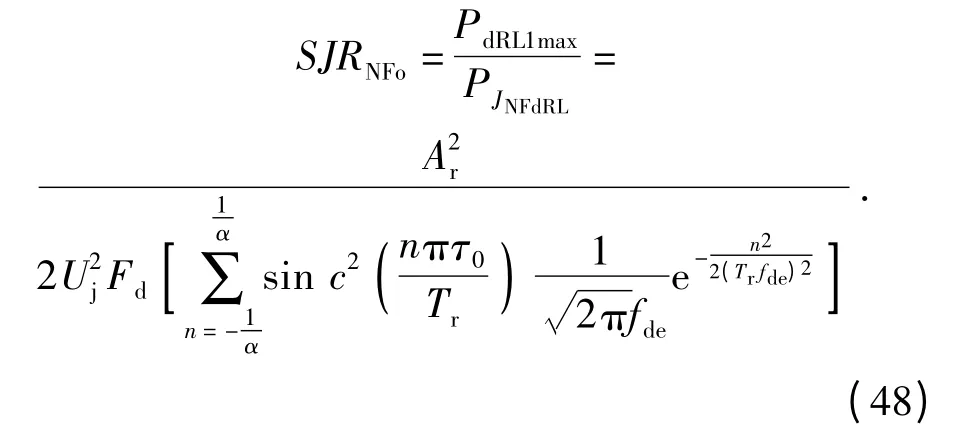
因此，噪声调频干扰作用下系统的处理增益量化表达式为

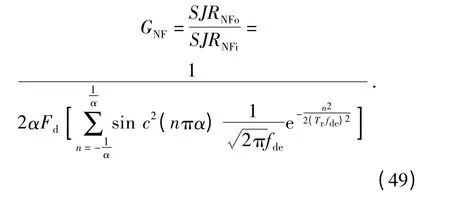
3 仿真与讨论

根据PD 引信的工作原理，基于MATLAB 构建了PD 引信仿真模型，并针对3 种有源噪声干扰，进行仿真验证，计算其处理增益。仿真工作参数设置如下:脉冲调制周期Tr=4 000 ns;脉冲宽度τ0=20 ns;脉冲占空比α = 0.005;多普勒频率fd=40 kHz;多普勒滤波器截止带宽Fd=66.7 kHz;仿真距离30 m;预定炸高15 m;距离门延迟τi=100 ns;信号幅值1 V.

在仿真验证过程中，采用了Monte Carlo 实验方法来消除噪声随机性的影响。具体实现步骤如下:

1)将有源噪声干扰加入到PD 引信仿真模型中，获得仿真所得的处理增益G(n).

2)在保持高斯白噪声均值、方差不变的情况下，通过改变其初始种子来构造N 个独立的有源噪声随机过程干扰，重复上述仿真过程，并计算仿真获得处理增益的平均值及方差。

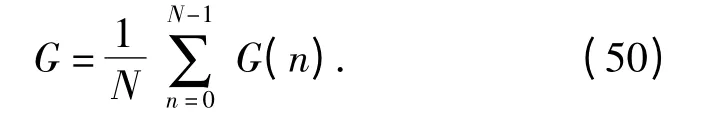
仿真验证中取N =50，初始种子取值范围为［31 -80］. 表1给出了仿真结果。在保证表1中干扰参数不变的情况下，图2和图3分别给出了在有源噪声干扰作用下，PD 引信处理增益同脉冲占空比α 与多普勒滤波器带宽Fd的关系图。

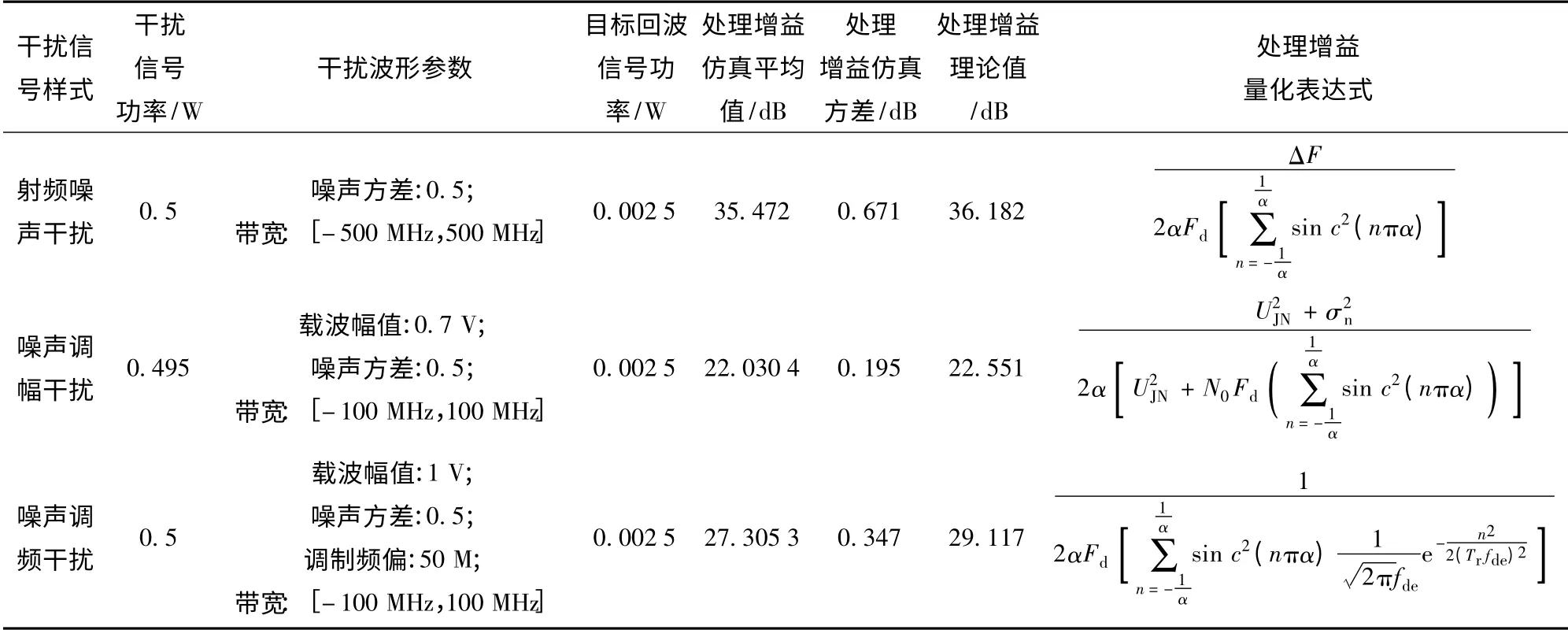
表1 PD 引信在不同有源噪声干扰作用下的处理增益Tab.1 Processing gains of PD fuze under different active noise jamming

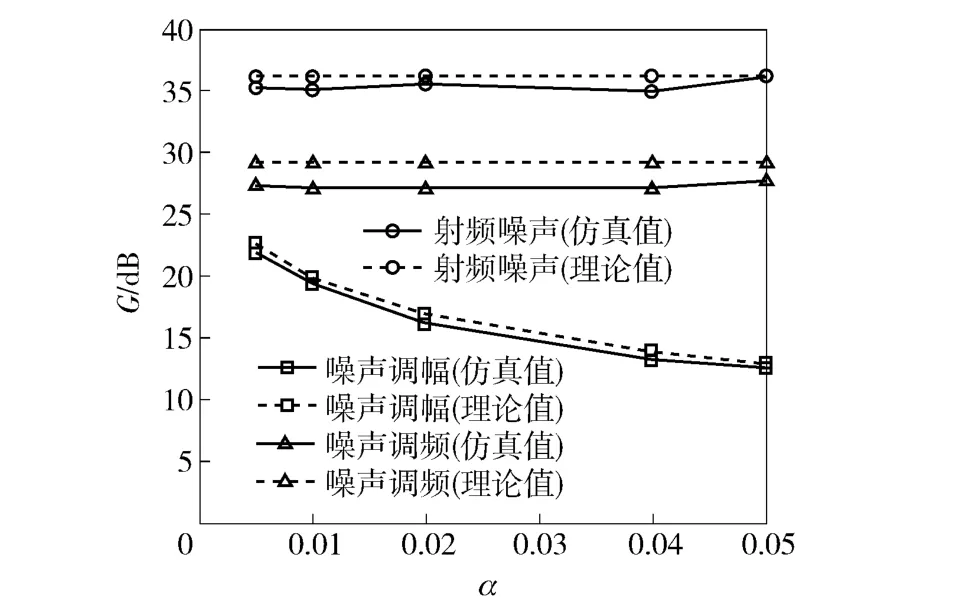
图2 不同占空比α 时处理增益Fig.2 Processing gains at different pulse duty cycle α

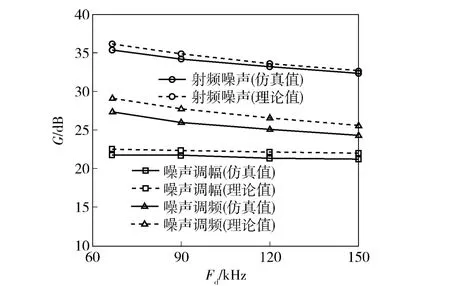
图3 不同多普勒滤波器带宽Fd 时处理增益Fig.3 Processing gains with different bandwidths Fd of Doppler filter

理论推导与仿真结果表明:

1)仿真所得处理增益与理论值相吻合，验证了射频噪声、噪声调幅与噪声调频干扰下PD 引信处理增益量化表达式的正确性。

2)有源噪声干扰样式中，噪声调幅干扰信号因为其功率谱能量主要集中在引信可接收的频带范围内，通过基带多普勒滤波器的信号成分多，所以对PD 引信的干扰效果较明显。

3)降低占空比α，在同样的干扰条件下，可降低输入信干比，但对不同种类的有源噪声干扰输出信干比的影响不同。对射频噪声和噪声调频干扰来说，距离门选通后可落入基带多普勒滤波器带宽内的功率谱成分会变少，输出信干比也相应降低，因而对射频噪声和噪声调频干扰作用下PD 引信的处理增益几乎没有影响。对噪声调幅干扰来说，由于距离门选通后可落入基带多普勒器带宽内的载波项不会发生变化，输出信干比较输入信干比变化小，因而可提高噪声调幅干扰作用下PD 引信的处理增益。

4)减少多普勒滤波器带宽Fd，对于3 种有源噪声干扰样式，通过基带多普勒滤波器的功率谱成分都会变少，因而可提高有源噪声干扰作用下PD 引信的处理增益。

仿真与理论的误差来源主要有两点:一是带通滤波器阶数较高所引起的延迟;二是基带多普勒滤波器为考虑采样率问题而选择模拟滤波器，通带内增益小于0.

4 结论

本文以处理增益为表征参量，基于功率谱，定量研究了PD 引信抗射频噪声、噪声调幅和噪声调频干扰的能力，揭示了有源噪声干扰对PD 引信的作用机理，为提高PD 引信抗有源噪声干扰性能而进行的参数优化设计提供了理论依据。理论推导和仿真验证表明:

1)由于距离门和基带滤波器的作用，PD 引信具有较强的抗有源噪声干扰能力。同等干扰功率下，PD 引信对于3 种有源噪声的抗干扰能力，由强到弱依次为:射频噪声干扰、噪声调频干扰、噪声调幅干扰。

2)PD 引信抗有源噪声干扰的能力主要同脉冲占空比α 和多普勒滤波器带宽Fd有关:降低占空比α(针对射频噪声干扰和噪声调频干扰来说，作用并不明显)，减少多普勒滤波器带宽Fd，均可以提高PD 引信抗有源噪声干扰的能力。

References)

［1］Brown L. The proximity fuze［J］. IEEE Aerospace and Electronic Systems Magazine，1993，8 (7):3 -10.

［2］梁棠文，李玉清，蒲开忠，等. 防空导弹引信设计及仿真技术［M］. 北京:宇航出版社，1995:199 -250.LIANG Tang-wen，LI Yu-qing，PU Kai-zhong，et al. Design and simulation technology of fuze for air defense missile［M］. Beijing:China Astronautic Publishing House，1995:199 -250. (in Chinese)

［3］崔占忠，宋世和，徐立新. 近炸引信原理［M］. 第3 版. 北京:北京理工大学出版社，2009:112 -119.CUI Zhan-zhong，SONG Shi-he，XU Li-xin. Principle of proximity fuze［M］. 3rd ed. Beijing:Beijing Institute of Technology Press，2009:112 -119.(in Chinese)

［4］赵惠昌. 无线电引信设计原理与方法［M］. 北京:国防工业出版社，2012:147 -161.ZHAO Hui-chang. Fundamentals and methodology of radio fuze［M］.Beijing:National Defense Industry Press，2012:147 - 161. (in Chinese)

［5］周新刚，赵惠昌，涂友超. 脉冲多普勒引信抗干扰性能评判方法和仿真［J］. 系统仿真学报，2011，23(1):207 -211.ZHOU Xin-gang，ZHAO Hui-chang，TU You-chao. ECCM evaluation and simulation of pulse doppler fuze［J］. Journal of System Simulation，2011，23(1):207 -211.(in Chinese)

［6］周新刚. 基于模糊函数切割法的典型无线电引信抗干扰性能测度［D］. 南京:南京理工大学，2009:83 -101.ZHOU Xin-gang. Evaluation of anti-jamming capability of typical radio proximity fuzes based on ambiguity function incision［D］.Nanjing:Nanjing University of Science and Technology，2009:83 -101.(in Chinese)

［7］赵惠昌，周新刚. 基于模糊函数切割法的线性调频连续波引信抗干扰性能测度［J］. 兵工学报，2009，30(12):1591 -1595.ZHAO Hui-chang，ZHOU Xin-gang. Anti-jamming performance evaluation of linear frequency-modulated continuous wave fuze based on ambiguity function incision［J］. Acta Armamentarii，2009，30(12):1591 -1595. (in Chinese)

［8］涂友超，赵惠昌，周新刚.噪声调频干扰下伪码调相引信启动概率分析［J］. 南京理工大学学报，2011，35(2):252 -256.TU You-chao，ZHAO Hui-chang，ZHOU Xin-gang. Analysis on starting probability of pseudo-random binary-phase-coded fuze under noise FM jamming［J］. Journal of Nanjing University of Science and Technology，2011，35(2):252 -256. (in Chinese)

［9］闫岩，崔占忠. 超宽带无线电引信抗干扰性能研究［J］. 兵工学报，2010，31(1):13 -17.YAN Yan，CUI Zhan-zhong. Anti-jamming performance of ultra wideband radio fuze［J］. Acta Armamentarii，2010，31(1):13 -17.(in Chinese)

［10］周新刚，赵惠昌，涂友超，等. 基于多普勒效应的伪码调相及其与PAM 复合引信的抗噪声性能分析［J］. 电子与信息学报，2008，30(8):1874 -1877.ZHOU Xin-gang，ZHAO Hui-chang，TU You-chao，et al. Performance analysis concerning anti-noise for pseudo-random code phase modulation and pulse amplitude modulation combined fuze based on doppler effect［J］. Journal of Electronics ＆ Information Technology，2008，30(8):1874 -1877.(in Chinese)

［11］刘己斌，赵惠昌，陆建伟. 几种伪码体制引信的抗噪声性能分析［J］. 兵工学报，2005，26(1):20 -24.LIU Ji-bin，ZHAO Hui-chang，LU Jian-wei. Performance analysis concerning anti-noise for several pseudo-random code fuzes［J］.Acta Armamentarii，2005，26(1):20 -24.(in Chinese)

［12］熊刚，杨小牛，赵惠昌. 伪码调相与正弦调频复合引信抗噪性能分析［J］. 现代雷达，2007，29(12):12 -17.XIONG Gang，YANG Xiao-niu，ZHAO Hui-chang. Performance analysis of anti noise of pseudo-random PM and sine frequency modulation combined fuze［J］. Modern Radar，2007，29(12):12 -17.(in Chinese)

［13］赵国庆. 雷达对抗原理［M］. 第2 版. 西安:西安电子科技大学出版社，2012:122 -143.ZHAO Guo-qing. Principle of radar countermeasure［M］. 2nd ed. Xi＇an:Xidian University Press，2012:122 -143. (in Chinese)